水下单兵火箭弹弹道计算
2018-12-04龚铂淳马少杰
龚铂淳,马少杰,魏 健
(南京理工大学 机械工程学院,南京 210094)
近年来,我国南海海域冲突不断升级,国土安全面临着严峻的挑战。面对复杂多样的现代海洋战场,各种水下武器的研制成为了当下研究的热点[1]。在本文中所要研究的对象——水下单兵火箭弹有着大威力、高速度、高精度的特点,完全符合现代海洋战争的需求。通常用于水下武器引信的解保环境力有以下几种,爬行力、火药燃气、弹体压力、水流冲击力等[2]。本文考虑到,水的阻力远大于空气,所以火箭弹在水下做衰减运动的过程中会受到较大爬行阻力的作用,据此在火箭弹引信的设计中,提出将水下的爬行力作为解保环境力的设想。为了验证这一设想,需要对水下火箭弹的运动过程进行分析,求解出速度和加速度等运动学参数,以此推算是否有足够的爬行力解除保险。
目前水下火箭弹的相关研究,主要是针对火箭弹从静止开始发射的单一弹道[3]。本研究根据水下单兵火箭弹的特点,对单一火箭弹弹道进行完善,分析了火箭弹在水下抛射和火箭助推的运动全过程。用MATLAB解算弹道方程,得出速度和加速度随时间变化的曲线图。结合计算结果,分析火箭弹在运动过程中的运动学和动力学参数,验证爬行力作为解保环境力的可行性。这对水下火箭弹引信保险机构的设计,以及水下火箭弹的射击精度和可靠性都具有重要意义。
1 火箭弹水下弹道特性分析
为了减少误差、提高仿真精度,需要先行对弹道特点进行分析,为弹道仿真方案的设计提供参考和支撑[4]。水下火箭弹的工作原理可以参照陆上火箭弹的弹道特性进行分析[5],如图1所示。火箭弹先由发射架进行抛射,在短时间内获得一个较大的初速度,随后在水的阻力作用下,速度迅速衰减。等达到一定安全距离后,火箭发动机点火进行二次加速,火箭弹速度衰减变慢,在一段时间后速度开始缓慢回升。随后发动机停止工作,火箭弹失去推力,速度再次迅速衰减。根据以上弹道特性,火箭弹在水下运动的全过程包括抛射和火箭助推后的两部分,为了方便说明,下文将火箭助推部分的弹道称为第二段弹道。本文主要研究在一定初速度下,火箭弹在水下运动的全过程。
1.1 建立火箭弹水下模型
水下火箭弹的运动遵循牛顿力学定律、质量和能量守恒定律等。相关领域的研究以往集中在鱼雷的航行力学上,鉴于其和鱼雷在外形上差别不大,主要是发动机的输出方式不同,所以水下火箭弹的主动段弹道计算可以借鉴鱼雷航行力学的有关知识[6]。据此进行如下模型假设:
1) 流体无黏性,不可压缩。
2) 流体是无限的,在航行器运动之前是静止的。
3) 火箭弹为刚体,其外形关于xOy、xOz平面对称。
4) 火箭弹重心与浮心距离较小,浮心处速度与质心处速度相等。
5) 不考虑火箭弹的偏航运动。
6) 火箭弹在运动过程中,其质量与质量分布保持不变。
在考虑初速度下根据所作的模型假设对航行体在水下的运动过程进行受力分析,如图2所示。
1.2 水下火箭弹水下运动受力分析
根据图2中的受力分析,列举水下火箭弹所受的力及其公式[7]:
1) 阻力
式中:CxS为阻力因数;S为鱼雷最大横截面积。
2) 法向流体动力(升力)
3) 俯仰力矩
沿弹体坐标系OZ轴(横轴)的力矩称为俯仰力矩,因为它的作用效果使航行器产生俯仰运动。俯仰力矩也称为纵向力矩。俯仰力矩为位置导数可表示为
4) 旋转运动的阻力及阻力矩
5) 非定常运动附加惯性力
2 水下火箭弹纵向运动方程组
2.1 纵向运动方程的基本假设
火箭弹在水下的运动可以分解为纵向运动与侧向运动,纵向运动为一平面运动,其运动平面与火箭弹的纵对称面重合,且为空间垂直平面。而侧向运动是指其在水平面的运动,包括火箭弹在水平面内的运动和绕轴转动。为了避免由于数学模型过于复杂而造成分析和处理上的困难,故而要在条件允许范围内尽可能简化模型[8]。显然,本研究的对象是火箭弹在水下的纵向运动,因此为了将其分离出来单独研究,再对模型做如下假设:
1) 弹体对其纵对称面是对称的,在纵向运动中,不产生侧向力、偏航力矩和横滚力矩。
2) 弹体纵对称面保持在垂直面内。
3) 火箭弹弹道为垂直面内的平面弹道。
2.2 水下火箭弹纵向运动方程组
根据上文对火箭弹在水下全过程的分析,水下火箭弹纵向运动方程组包含了抛射弹道和第二段弹道方程组两部分。充分考虑火箭弹在抛射段和第二段所受的不同外力,分别列出上述两部分弹道方程组。
火箭弹在水下的空间运动方程组由动力学方程组和运动学方程组组成。据动量和动量矩定理,将弹体的全部外力及外力矩代入式(1)中,即是动力学方程组。运动学方程组由式(2)~式(5)组成,分别是攻角及侧滑角与速度分量之间的关系、速度坐标系到地面坐标系的转换方程、弹体坐标系到地面坐标系的转换方程、弹体角速度在弹体坐标系中的投影[9]。
(1)
(2)
(3)
(4)
(5)
根据上文关于分离纵向运动方程的假设,则地面坐标系、弹体坐标系、速度坐标系、半速度坐标系都是同一平面,首先结合火箭弹在水下的空间运动方程组,推导出在纵向平面内水下火箭弹的抛射段弹道如下:
(6)
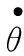
火箭助推后,在原有抛射弹道方程组的基础上,再考虑火箭推力和燃料质量随时间的变化,可得纵平面内水下火箭的第二段弹道方程组如下:
(7)
式中:m1为火箭弹质量随时间t变化的函数;Tt为火箭弹所受的推力随时间t变化的函数,其他参数的定义与抛射段弹道方程组保持一致。
2.3 附加惯性质量
附加质量是水下物体运动分析的重要参数。物体在流体中变速运动,推动物体的力不仅要为增加物体的动能做功,还要为增加周围流体的动能做功。因此质量为m的物体要获得加速度a,施加在它上面的力F将大于物体质量m与加速度a的乘积,增加的这部分质量就是附加质量。某些物体的附加质量数值较大,不容忽略[10]。
坐标系选定后,水下航行器的附加质量仅与其几何形状有关。在上文的建模中,假设水下航行器具有两个对称面,即同时关于及两个平面对称,则不为零的附加质量有8个,即λ11,λ22,λ26,λ33,λ35,λ44,λ55,λ66,并且有λ33=λ22,λ66=λ55,λ55=-λ26,进一步简化可得:
通过数值计算来模拟物体附加质量的试验测量过程,物体在流场中按照设定的运动规律做非定常运动,监控流体对物体的作用力及力矩,通过对物体受力的分析,从中提取包括物体的附加质量在内的流体动力参数。为了计算上述各分量,需要模拟回转体沿x轴、y轴加速运动及绕z轴的加速转动。使回转体沿y轴加速运动,通过监控升力系数和力矩系数Mz可以获得λ22和λ26;使回转体沿x轴加速运动,通过监控阻力系数Cx可以获得λ11;使回转体绕z轴加速转动,通过监控相应的力矩系数Mz可以获得λ66。
3 弹道计算
设火箭弹总质量(含火箭发动机和燃料)M=0.5 kg,燃料质量为50 g,燃烧持续时间为300 ms,假设火箭燃料均匀燃烧,故发射后弹的实际质量为m=0.5~170 kg,又海水密度p=1 024 kg/m,所以水下火箭弹所受浮力约为B=1.4 N,重力约为G=4.9 N。现忽略火箭弹从发射到获得一定初速度的短暂时间,假设某一时刻火箭弹的速度为80 m/s,并从此时开始计时,对火箭弹在水下运动的全过程进行弹道计算。设火箭发动机的推力曲线如图3所示。
由图3可得推力-时间的函数,表达式为
(8)
将上述模型假设中的所有参数代入水下弹道方程组(6)和方程组(7)中。上述两个方程组都是封闭的,设置水下火箭弹运动的初值条件,v=80 m/s,α=θ=0,运用MATLAB工具来求解弹道微分方程组,得到速度随时间变化的曲线如图4所示。
由图4可知:火箭弹在水下抛射的初速度为80 m/s,受到水下阻力的作用,速度迅速下降。T1时刻火箭发动机的工作,火箭的推力不断上升,水下火箭弹的速度衰减也逐渐变慢,并在60 ms处开始回升,此时火箭弹速度为30 m/s。在220 ms处,火箭弹速度达到最大值62 m/s,并在短暂时间内趋于稳定。随后火箭推力下降,水下火箭弹的速度又在短时间内迅速下降。在T2时刻,发动机燃料耗尽,速度最终趋于平缓。
火箭弹水下弹道方程组经过四阶龙格库塔解算后,每段方程得到40个数据,对所得数据进行非线性拟合,可得水下火箭弹速度拟合的分段方程组如下:
1) 当0 f(ν)=1.996×107t4-2.008×106t3+ 9.225×104t2-2899t+80 2) 当0.03 s f(ν)=1.548×105t4-9.232×104t3- 2.001×104t2-1576t+69.56 3) 当0.18 s f(ν)=1.09×107t4-1.0656×107t3+ 3.906×106t2-6.376×105t+3.914×104 4) 当0.27 s f(ν)=-4.184×106t3+3.894×106t2- 1.2134×106t+1.262×105 5) 当t>0.33 s时 f(ν)=-2.0245×105t4+4.488×105t3- 3.714×105t2+1.361×105t-1.869×104 对求得的水下火箭弹速度拟合方程组进行求导即可获得加速度方程组,绘制加速度随时间变化的曲线如图5所示。 由图5可知,火箭弹在水下抛射时受到的阻力很大,加速度绝对值达到250g。在抛射过程中,由于速度在不断衰减,对应的减加速度也在不断减小。在T1时刻发动机开始工作,推力不断上升,火箭弹的速度衰减继续减小,在60 ms处加速度变为正值,速度开始回升,加速度也不断增大,在120 ms处达到最大,约为30g左右。随后,发动力推力保持恒定,火箭速度趋于稳定,在230 ms处加速度回落至0。随后发动机推力减弱,加速度开始由0变为负值。在T2时刻,水下火箭弹完全失去动力,其减速加速度很明显,峰值达到65g左右。在失去动力后,火箭弹作自由运动,速度逐渐减小至0,加速度也对应地减小至0。 通过建立模型,对水下火箭弹进行受力分析,列出其在纵向平面下抛射段弹道和第二段弹道方程组。列举工程实例,利用MATLAB数学工具,求解得到水下火箭弹在有初速情况下的推力曲线,并绘制速度与加速度曲线。由曲线图得火箭弹在水下运动时速度和加速度随时间的变化规律,获得了爬行力的数值和持续时间,验证了火箭弹在水下运动过程中,爬行力足够大,持续时间足够长,可以作为引信的远解环境力,为后续引信保险机构设计提供了理论支撑。4 结论
