一类压缩比非一致且具完全重叠结构自相似集的迭代函数系

潘 俨,姚媛媛

(1.上海海事大学经济管理学院,上海 201306)

(2.华东理工大学理学院,上海 200237)

1 引言

研究产生自相似集的所有迭代函数系起源于图像压缩理论,是分形几何中一个基础而又重要的问题[1].

丰德军等在文献[1]中首先研究了多种条件下一些直线自相似集的最小生成迭代函数系.对于高维情况,讨论主要集中在满足开集条件或强分离条件的压缩比一致的自相似集[3,4]或几类特殊的高维自相似集[5,6].此外,邓国泰等[7]研究了直线自相似集平移交仍为自相似集时的所有迭代函数系族等.

以上研究结果或多或少依赖于某种分离条件.文[8]首次讨论了一类具完全重叠结构自相似集的所有迭代函数系.该类自相似集压缩比一致且证明讨论情况众多,较为复杂.本文拟推广文[8]中结论,讨论一类压缩比非一致且具完全重叠结构自相似集的迭代函数系.证明主要依赖于该类自相似集的gap性质,十分简洁.

定理1.1设g(x)=λx+b满足0<|λ|<1且b∈R.若g(E)⊆E,则存在正整数n和i1,···,in∈ {1,2,3} 满足 g(x)=fi1◦ ···◦fin(x).

2 定理证明

首先需要如下引理和定义.

引理2.1[6]设是欧氏空间自相似集F的一个迭代函数系.更进一步,假设对任意自相似压缩映射f满足f(F)⊆ F,均存在i∈{1,···,m},使得f(F)⊆ gi(F).设h是满足h(F)⊆ F 的一个相似压缩映射.则存在正整数n和i1,···,in∈{1,···,m},使得h(F)=gi1◦ ···◦ gin(F).

定义2.2称开区间(a,b)为集合E中的gap若a,b∈E且(a,b)∩E=∅.

定义 2.3 设 i1,···,in∈ {1,2,3},定义 Ei1···in=fi1◦ ···◦ fin(E).

定理1.1的证明 首先证明

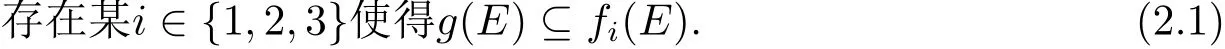
然后由引理2.1知存在正整数n和i1,···,in∈{1,2,3}满足g(E)=fi1◦···◦fin(E).又E非对称,故 g(x)=fi1◦···◦fin(x),定理获证.

设E中最大gap长度为A,则该gap位于E2与E3之间且A=1−2b−a(1−b).

由b≤a知E1∪E2中最大gap长度为aA(见下图).

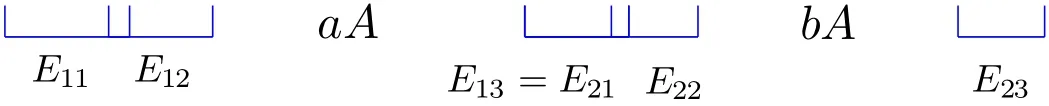
为证(2.1)式,使用反证法:假定g(E)⊆E且对任意i=1,2,3,有g(E)6⊆fi(E).由于g(E)中最大的gap长度小于A,故g(E)⊆E1∪E2.注意到E13=E21,从而g(E1∪E2)⊆E1∪E2=(E11∪E12)∪E2且E11∪E12与E2的距离为aA.由于g(E1∪E2)最大的gap长度小于aA,故g(E1∪E2)是E11∪E12或E2的子集.下面分情况讨论.

(1)g(E1∪E2)⊆E11∪E12.设ρg为自相似映射g的相似压缩比,因为g(E1∪E2)⊆E11∪E12=f1(E1∪E2),故可得|ρg|≤ a.因为E1∪E2不对称,故若|ρg|=a,则导致g=f1,与假设不符,故有|ρg|

(2)g(E1∪E2)⊆E2.下证g(E1∪E2)⊆E21∪E22或g(E1∪E2)⊆E23.

假设上述结论不成立,则g(E1∪E2)中最大gap的长度不小于E21∪E22与E23的距离,即 |ρg|·aA ≥ bA,从而 |ρg|≥.另一方面,又由 g(E1∪E2)⊆ E2知|ρg|·(b+a(1−b))≤ b,从而(b+a(1−b))≤b,得b(1−a)≤0,矛盾.

下面分别讨论上述两种情况.

情况1 g(E1∪E2)⊆E21∪E22=f2(E1∪E2).由上式知|ρg|≤b.因为E1∪E2不对称,故若|ρg|=b,则导致g=f2,与假设不符,故有|ρg|

情况2 g(E1∪E2)⊆E23.下证g(E3)⊆E23.否则g(E)的最大gap长度不小于bA,即 |ρg|·A ≥ bA,推出 |ρg|≥ b. 由 g(E1∪E2)⊆ E23知 |ρg|(b+a(1− b))≤ b2. 从而b(b+a(1−b))≤b2,矛盾.故g(E)⊆E23⊆E2,矛盾.

由反证法,(2.1)式获证.