高维BBM-Burgers方程解的衰减估计

徐红梅,朱丽丽

(河海大学理学院,江苏南京 211100)

1 引言

本文研究了多维空间Benjamin-Bona-Mahony-Burgers方程

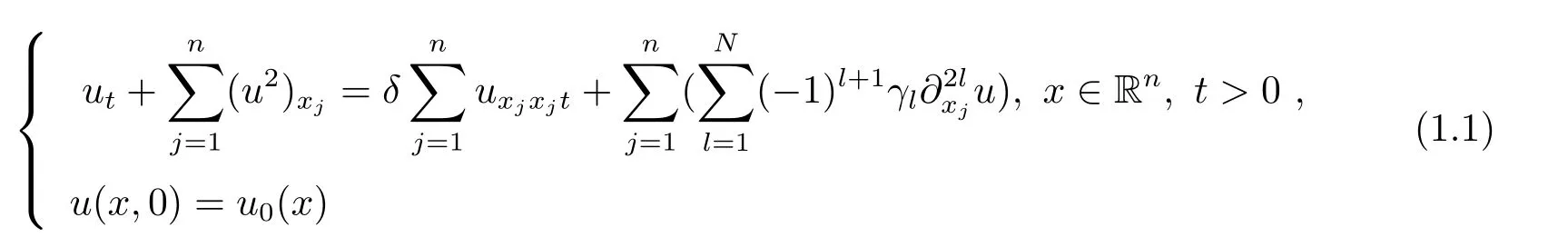
解的 L2衰减估计.此处n表示空间维数,n≥2,N ≥2正整数,δ,γl>0常数,Hl(Rn)是一般的Sobolev空间.

BBM方程是Benjamin,Bona和Mahony[1]在对流体动力学的物理研究中,由KorteweydeVries(Kdv)方程精炼而成.在描述非线性色散系统中小振幅长波的传播时,需要考虑耗散机制,由此产生了BBM-Burgers方程 (1.1).如文献 [1,2]指出,此方程中有不同的物理背景,称为粘性项和耗散项.关于此方程解的存在性和大时间状态得到了广泛的关注,很多数学工作者对其作出了详细研究.

当N=1时,Schonbek[3]讨论了方程(1.1)解的存在性和u(x,t;δ1,γ1)当δ→0,γ1→0时的收敛性.在文献[4]中,赵等人得到了N=2时方程(1.1)解的存在性和收敛性.在文献[5]中,王和张得到了N=2,空间维数2≤n≤6时解的整体存在性和衰减估计.在文献[6,7]中,Kondo和Webler分别给出了一维和多维空间情况下(1.1)解的存在性和收敛性.本文中,延续文[7]的结论,在解整体存在的前提下,研究解的衰减估计.

本文中,C表示一般常数,Lp为Lebesgue可测空间.F(f)或代表函数f(x)的傅里叶变换,且表示函数的逆傅里叶变换.

本文安排如下,在第二节中给出一些准备工作,如方程(1.1)的解的存在性结论,解的表达式等.第三节,用能量估计、时频分解等工具给出解的衰减估计.

2 准备工作

本文是在解的整体存在前提下做出的,为了读者方便,先列出文献[7]的结论.

定理2.1 若 u0∈则(1.1)式存在整体解 u∈C((0,∞);Hs(Rn)),s≥1+

对方程(1.1)的变量 x作傅里叶变换,得到

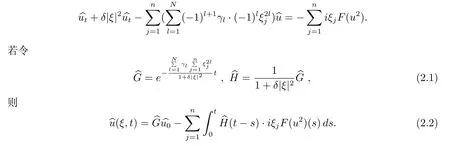
下面分析G的衰减.

证 由(2.1)式和Parseval等式,得

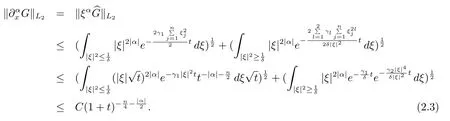
由(2.1),(2.3)式和Parseval等式,得

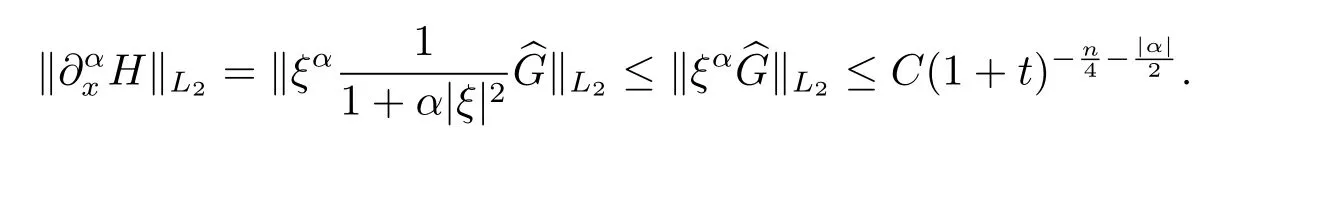
定理得证.

3 衰减估计

由能量积分,可得下述定理.

定理3.1若 u0∈H,可得 u∈H1(Rn).

证在(1.1)式两边同乘以 u,再关于变量 x积分得

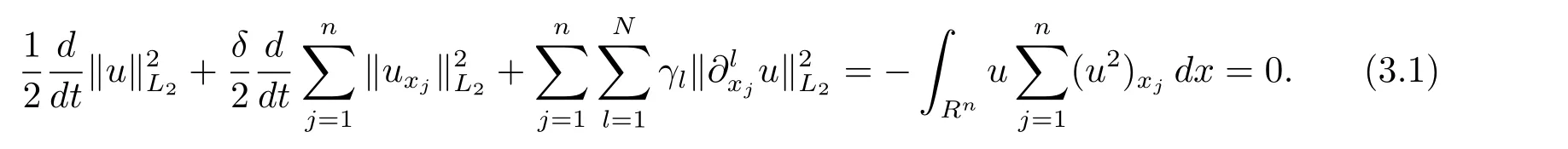
作光滑截断函数χ0(η)=定义时频算子χ(t,D),它的特征 χ(t,ξ).令 uL(x,t)=χ(t,D)u(x,t),则对 uL(x,t)有下述估计.

定理3.2当u0∈L1,有k∂xαuL(x,t)kL≤C

证 由(2.2)式和Minkowski不等式,得

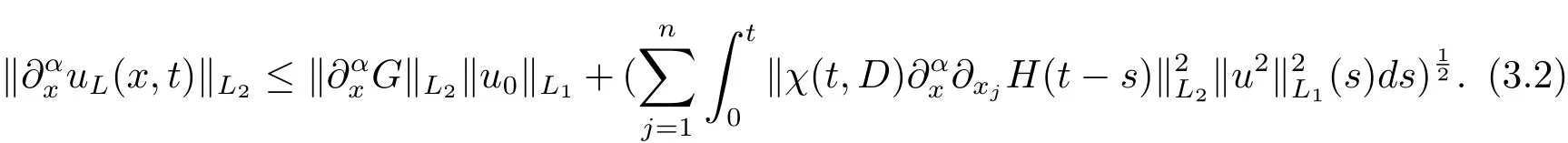
由 u0∈L1和定理2.2,

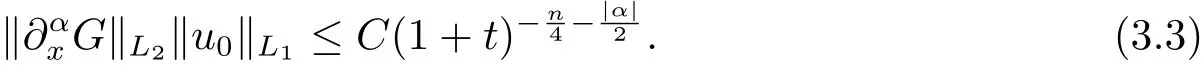
由定理3.1和(2.1)式,得

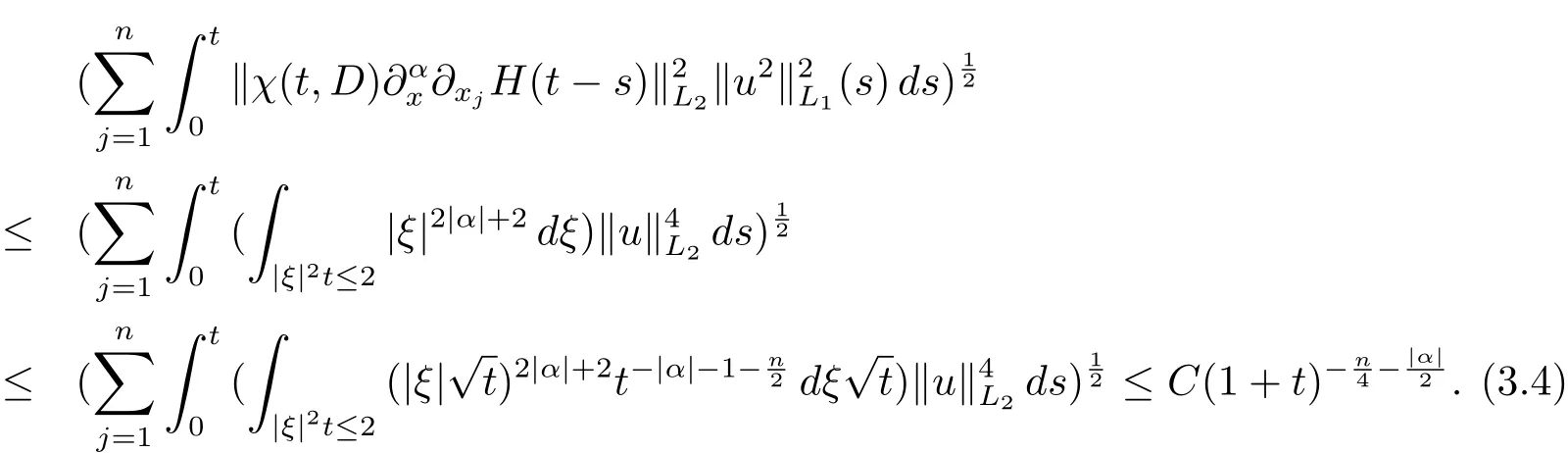
由(3.2)–(3.4)式,定理得证.

定理 3.3 kukH1(Rn)≤ C

由(3.5),(3.6)和(3.1)式,得

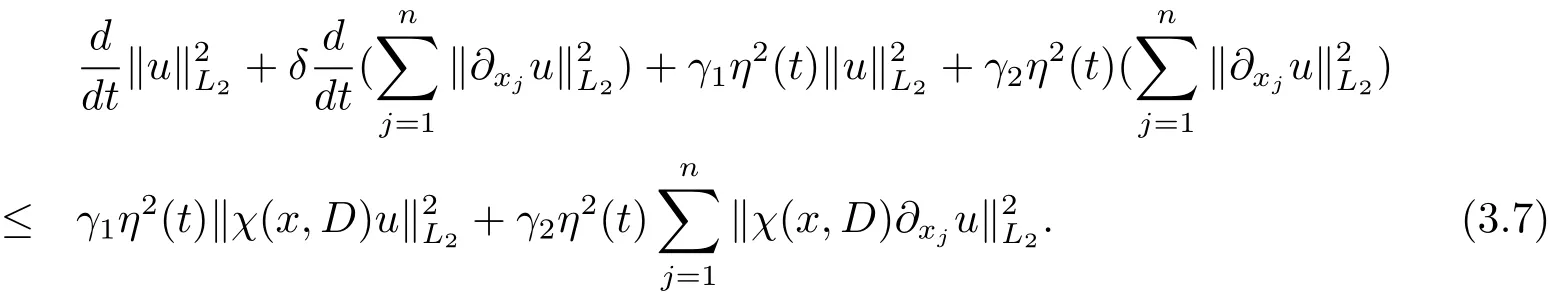
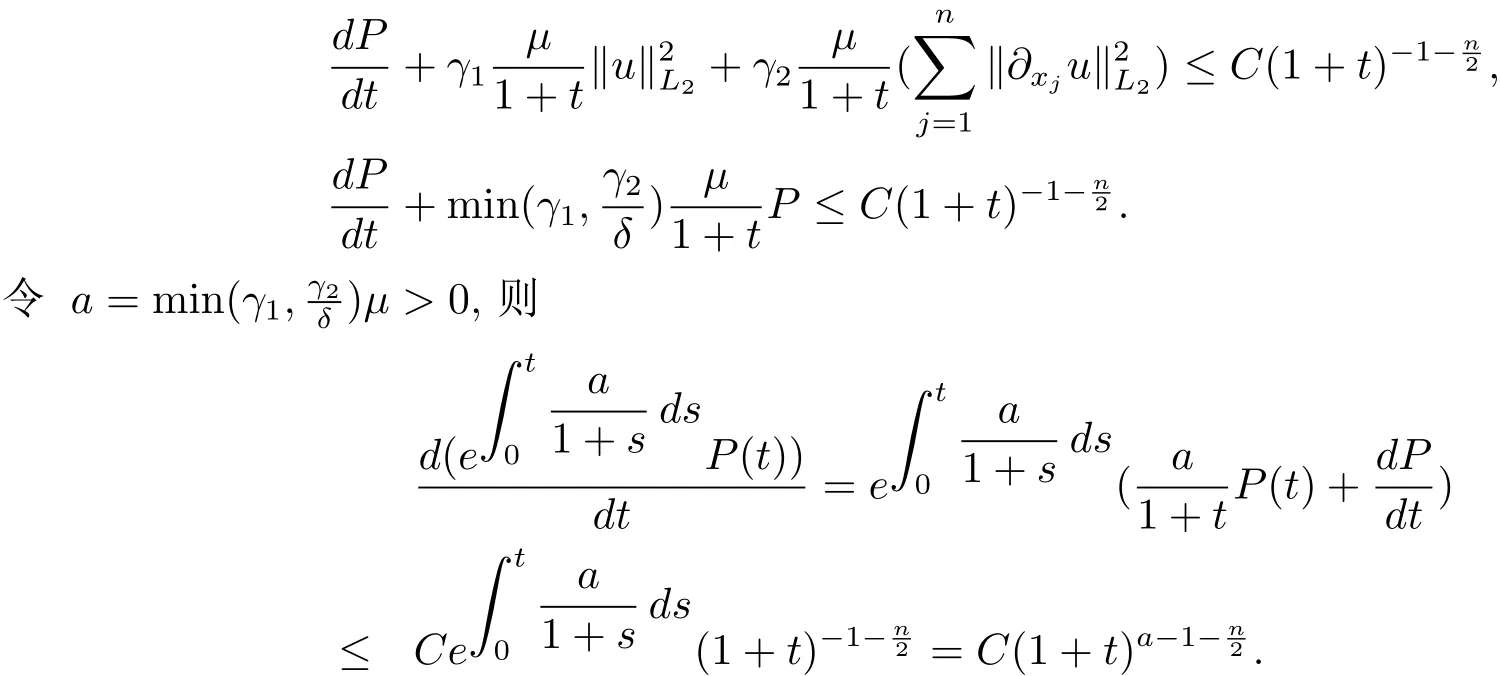
再由数学归纳法可得本文结论.

证 当 |α|=0时,由定理3.3可得.由(2.2)式和Minkowski不等式,有

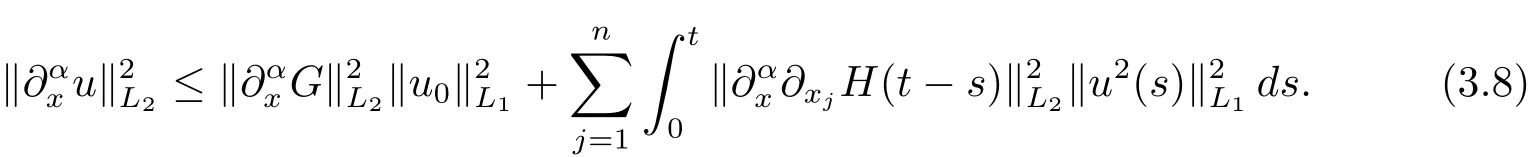
当 |α|=1时,由定理2.2和定理3.3得

由(3.3),(3.8)和(3.9)式得,当 |α|=1时,定理成立.

假设当 |α|=k 时,定理成立. 则当 |α|=k+1 时,不妨设 α =(α1,α2,···,αn) 且α1>1. 令 β =(α1− 1,α2,···,αn),则 |β|=k,且

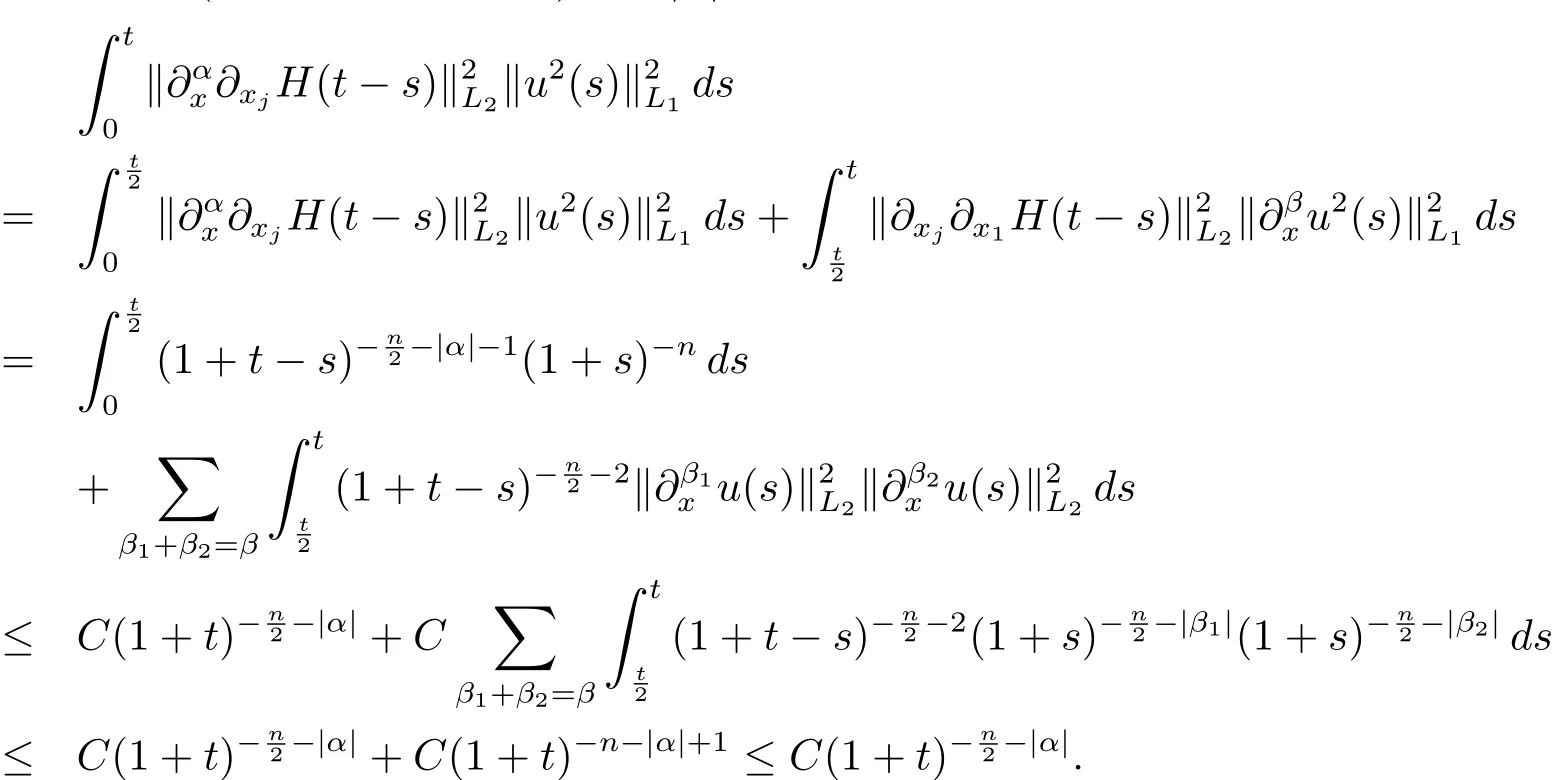
由数学归纳法

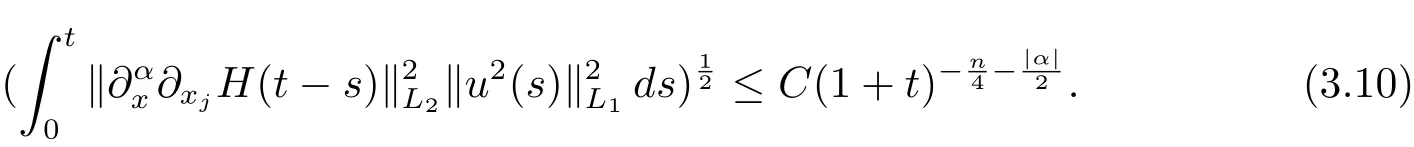
由(3.3),(3.8)和(3.10)式,定理得证.