A MODIFIED STRATEGY IN ALTERNATING NON-NEGATIVE LEAST SQUARES FOR NON-NEGATIVE MATRIX FACTORIZATION

LI Xiang-li,ZHANG Wen,YU Jiang-lan(School of Mathematics and Computing Science;Guangxi Key Laboratory of Cryptography and Information Security;Guangxi Key Laboratory of Automatic Detecting Technology and Instruments,Guilin University of Electronic Technology,Guilin 541004,China)

Abstract:In this paper,we study the global convergence of non-negative least squares(ANLS)for NMF.By applying a modified strategy to guarantee the existence of the limit point,we obtain the limit point is a stationary point of NMF.In addition,we give generalized modified strategies.Numerical experimental results show the above strategies are effective.

Keywords:non-negative matrix factorization(NMF);alternating non-negative least squares(ANLS);modified strategy

1 Introduction

Non-negative matrix factorization(NMF)[1]is different to other factorization methods because non-negative constraints are imposed.This makes factorization results more sense in the real word.

NMF attempts to decompose a given nonnegative matrix A into the product of a nonnegative basis matrix W and a non-negative coefficient matrix H,which can be interpreted as follow

where A ∈ Rm×n,W ∈ Rm×rand H ∈ Rr×n.The factorization results show that NMF can generate a reduced representation of the original date.In this sense,NMF is useful for extracting parts-based representations.

In recent years,NMF,as a parts-based representation of data,received considerable attentions in machine learning,signal processing,computer vision and so on[2–5].

In order to decrease the approximation error between A and WH,NMF be expressed as a constrained optimization problem

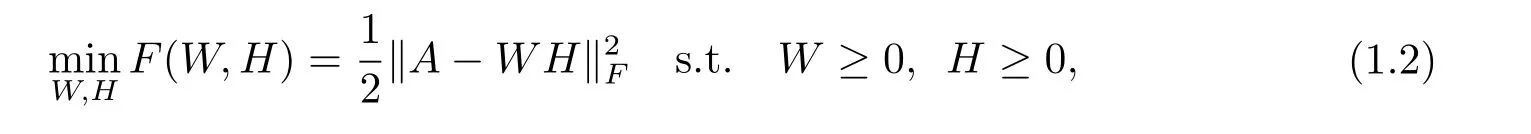
where k·k is the Frobenius norm,and W≥0(H≥0)means that all elements of the matrix W(H)are nonnegative.Kush-Kuhn-Tucker(KKT)[6]conditions for problem(1.2)are expressed as follows

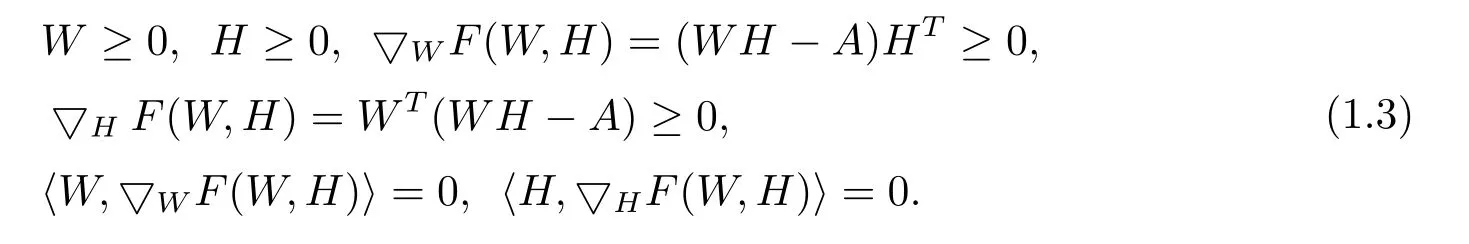
Alternating non-negative least squares(ANLS)[2,7,8]works well in practice,whose convergent speed is fast and elements not be locked.Iterate the following until a stopping criterion is satisfied

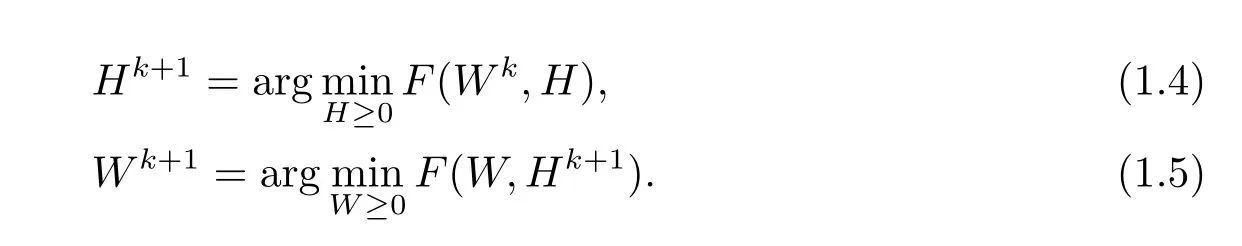
Clearly,F(Wk,H)and F(W,Hk+1)is convex,respectively.

ANLS is widely used as an efficient computational method for NMF,but the ANLS has a serious problem that its global convergence is not guaranteed in theory.In other words,for any initial solution,the sequence of ANLS contains at least one limit point and this limit point is a stationary point of NMF.The main difficulty in proving global convergence is that the existence of the limit point.

In[9],authors proposed a modified strategy and applied it to ANLS.The modified strategy is valid for proving global convergence.Motivated by the works of[9],we present a modified strategy to guarantee the existence of the limit point,and the limit point is a stationary point of NMF.In addition,we give generalized modified strategies.We can apply it in reality.

The rest of this paper is organized as follows.Our modified strategy is given in Section 2.Convergence analysis is established in Section 3.In Section 4,we give two generalized modified strategies.Finally,we conclude this paper in Section 5.

We sum up here briefly our notations.Let

Let B=Rm×n,hA,Bi=Tr(ABT).A·idenotes the i-th column of A,Ai·denotes the i-th row of A.Let kxk denote any norm of a vector,and kxk2denote 2-norm of a vector x.

2 Algorithm for Updating and Element of Matrix

In this section,based on the literature[9],we will present our modified strategy.Let(Wk,Hk)be generated by alternating non-negative least squares(ANLS).

First,we state the modified strategy of[9]be given as follows

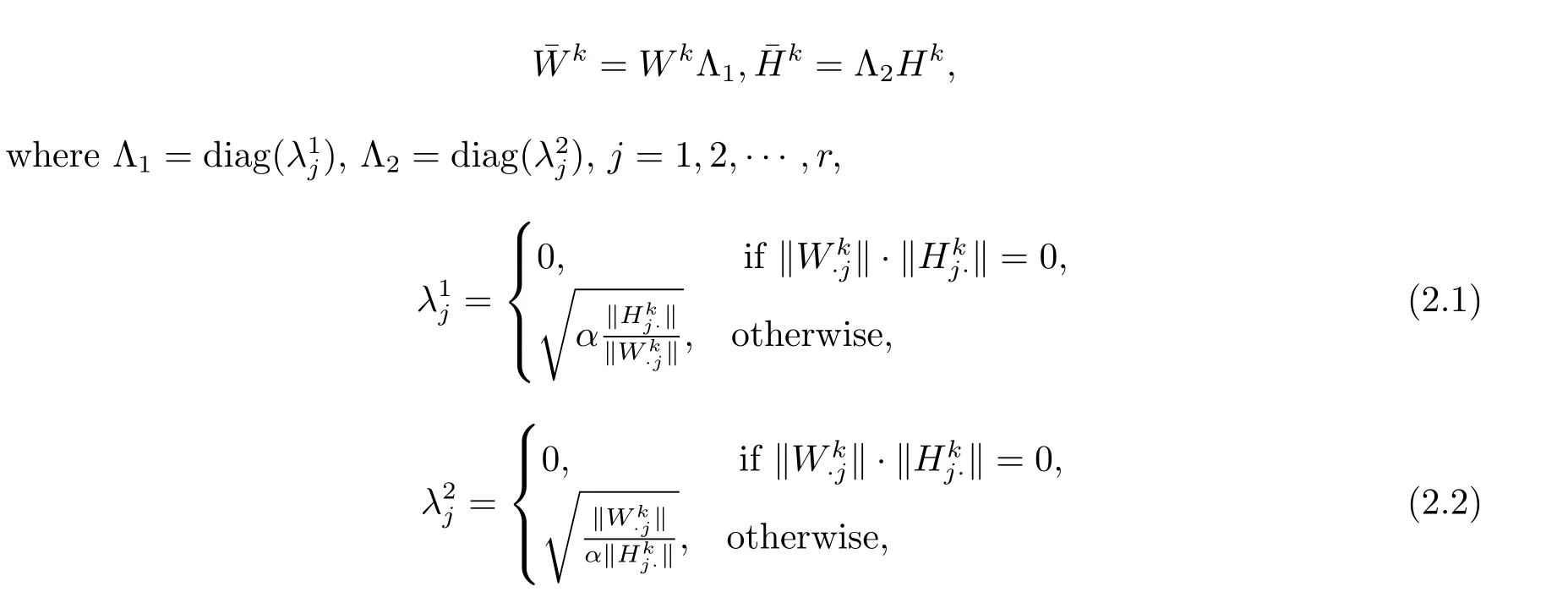
where α is a positive constant.The above strategy can ensure ANLS is convergent.

Motivated by the work of[9],we give another modified strategy.In NMF,we have the fact that

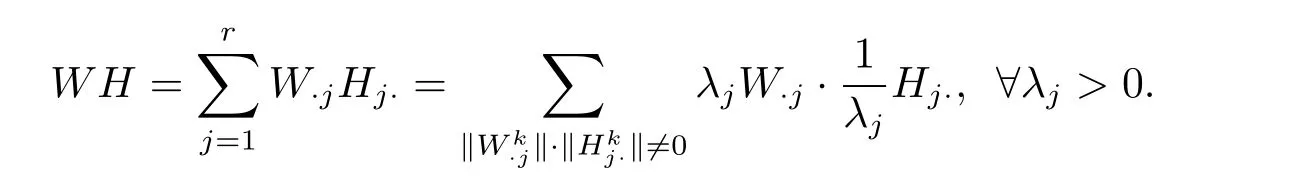
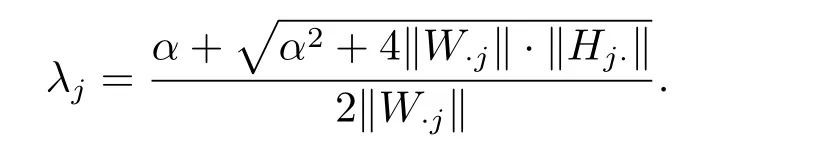
Hence,our modified strategy be described as follows:where Λ1=diagΛ2=diag(),j=1,2,···,r,

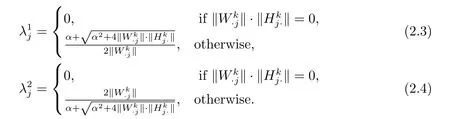
3 Algorithm

Based on the above analysis,in this section,we report ANLS with Strategy 1 for NMF as follows.

Algorithm 1(s.1)Give the starting point()≥0 and α ≥0.Set k=1.

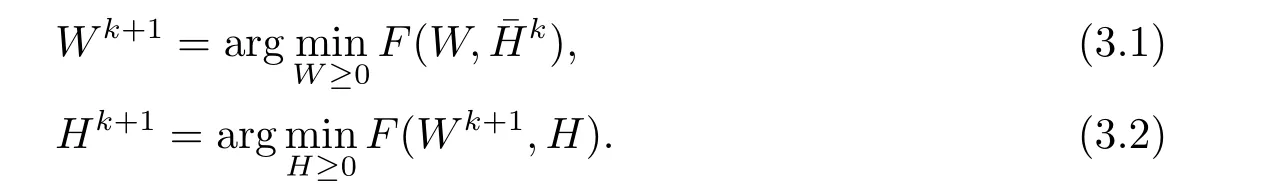
(s.3)Modified(Wk+1,Hk+1)to()using Strategy 1.

(s.4)Let k=k+1.Go to s.2.

4 Convergence Analysis

Similar to[9],the function of(1.4)((1.5))has a global minimizer on.In this section,we come to study the global convergence of the algorithm.

Proof Hkis a stationary of F(Wk,H),we have h(Wk)T(WkHk−A),Hk=0i,

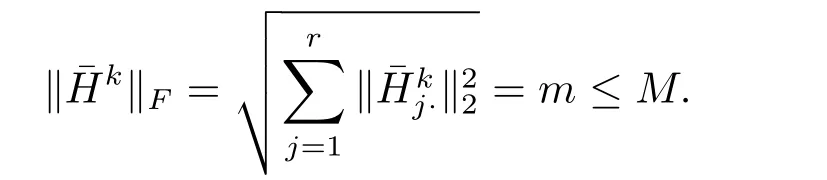
Similarly,we can get the conclusion that k¯WkkFis bounded.Therefore,is bounded.

Since the above theorem corresponds to[9,Theorem 2]and the proof is the same as that in[9,Theorem 2],we will omit it here.

5 Generalized Modified Strategies

From the above results,α is a positive constant no matter Strategy 1 or the strategy of[9].We might as well replace α with g(α),in which g(α)is a function of α and g(α)>0.Thus,we can get two generalized modified strategies.

The convergence of ANLS also is established when g(α)>0.In reality,we can let g(α)=or g(α)=e−αand so on.For different application problems,the choose of g(α)is different.

6 Numerical Experiments

In this section,we give some numerical experiments for the proposed modified strategies.We apply these strategies to the following algorithms:SBBNMF[9],BBNMF[10]and PGNMF[11].All codes of the computer procedures are written in MATLAB and run in MATLAB 7.10,and are carried out on a PC(CPU 2.13GHz,2G memory)with Windows 7 operation system environment.

In experiments,we will compare the following statistics:the number of inner iterations(Iter),the number of outer iterations(Oter),the objective function value(Fun),the residual function value(Res),and the CPU time in second(Time).The Res formula is similar to[9],and the initial parameters

In order to avoid the initial point affect the numerical result,in every experiment,we use 30 initial points,and every initial point is randomly generated.We list the following four experimental tables for different α.

The three tables indicates the proposed modified strategies are utility for these algorithms(SBBNMF,BBNMF,and PGNMF)of ANLS framework.In some experiments,Iter(Oter)is not an integer,because we test the average value the 30 initial point.In other words,Iter(Oter)represents the average number of iterations.

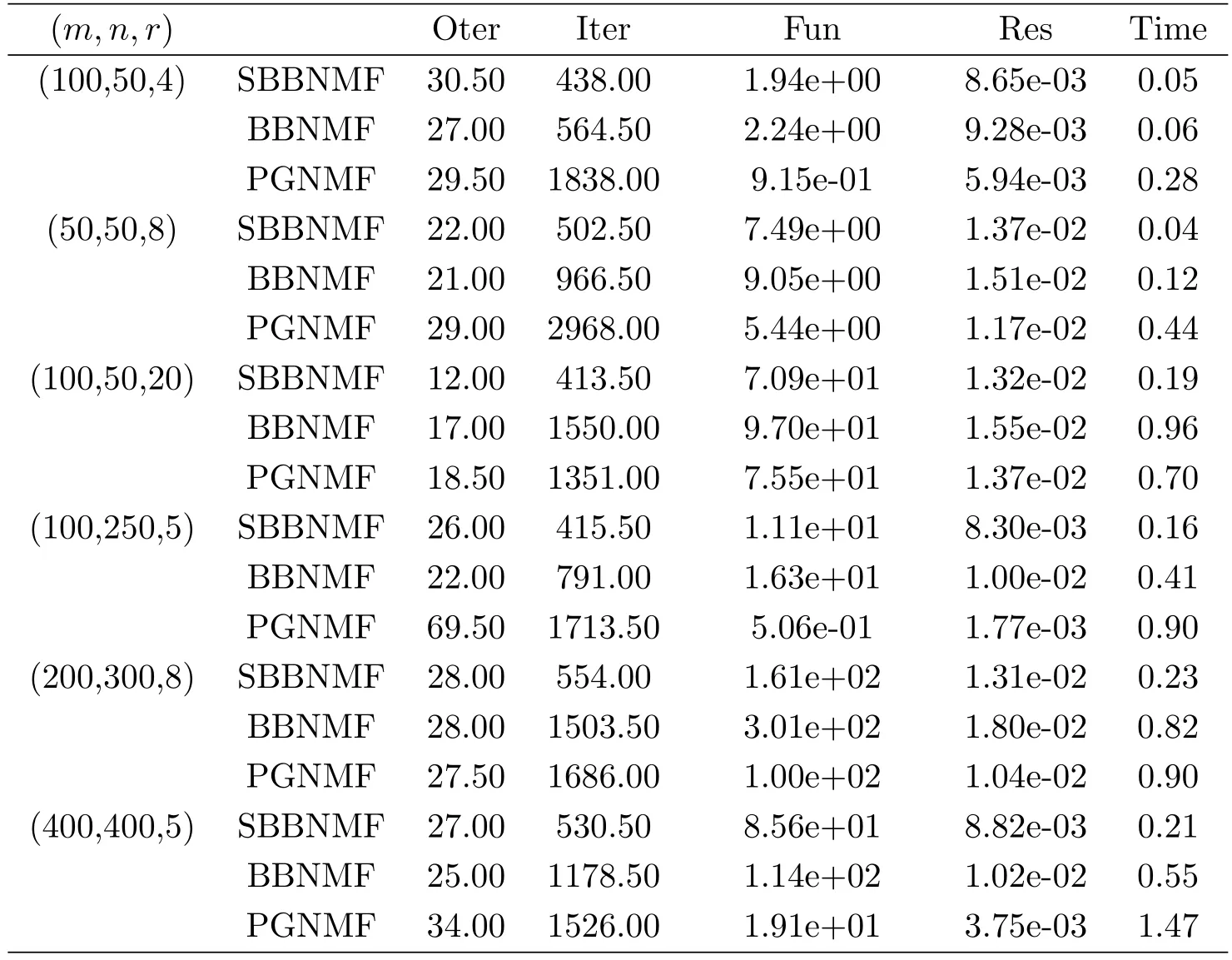
Table 1:A=abs(randn(m,r))∗abs(randn(r,n)),α =1

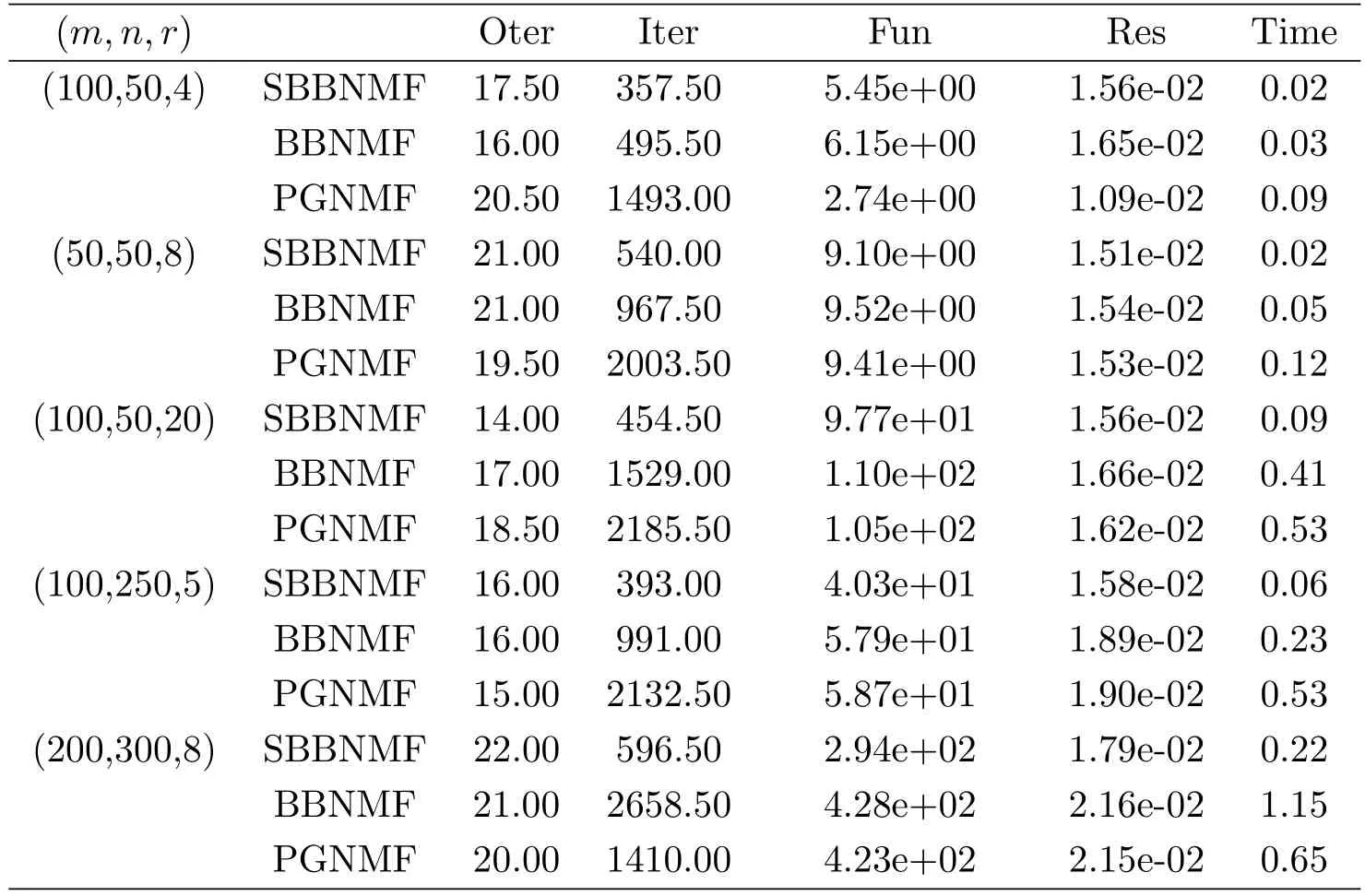
Table 2:A=abs(randn(m,r))∗abs(randn(r,n)),α =0

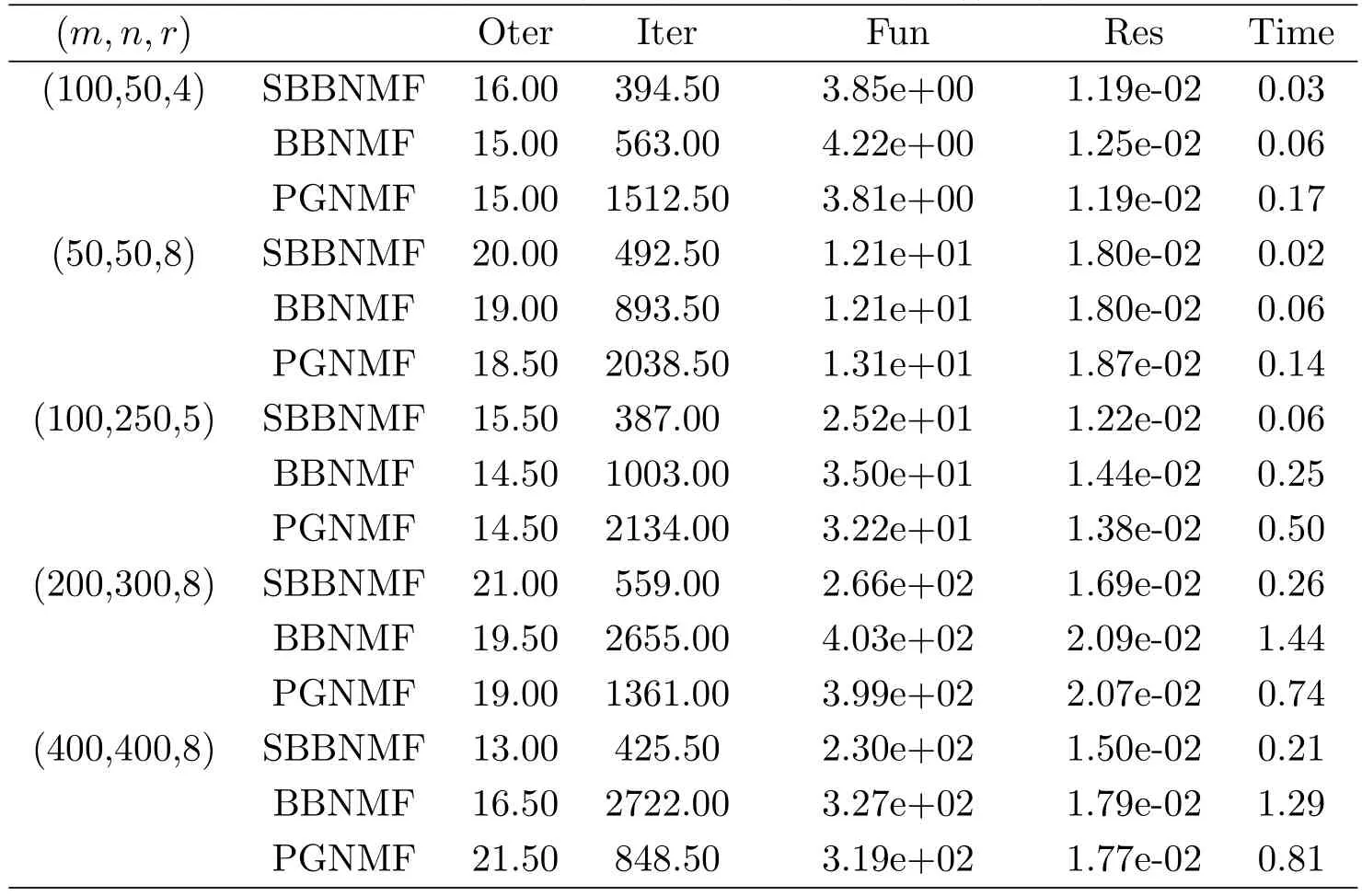
Table 3:A=abs(randn(m,r))∗ abs(randn(r,n)),g(α)=e−α

7 Convergence Analysis

Nonnegative matrix factorization(NMF)is not only a well-known matrix decomposition approach but also an utility and efficient feature extraction technique.In this paper,we propose a modified strategy,which can ensure the convergence of ANLS.In addition,we give generalized modified strategies.