Fuzzy Stability of the Orthogonal Cauchy Functional equations

BI Lv-qing,DAI Song-song,HU Bo

(1.School of Electronics and Communication Engineering,Guangxi Colleges and Universities Key,Laboratory of Complex System Optimization and Big Data Processing,Yulin Normal University,Yulin 537000,P.R.China;2.School of Information Science and Engineering,Xiamen University,Xiamen 361005,P.R.China;3.School of Mechanical and Electrical Engineering,Guizhou Normal University,Guiyang 550025,P.R.China)

Abstract:In this paper,we establish fuzzy stability of the orthogonal Cauchy functional equations

Key words:Fuzzy normed space;Hyers-Ulam stability;Orthogonally Cauchy functional equation;Orthogonally Cauchy functional Pexider equation;Orthogonality space

§1. Introduction

Stability problem of a functional equation was first posed by Ulam[1]which was partial answered by Hyers[2]and then generalized by Aoki[3]and Rassias[4]for additive mappings and linear mappings,respectively.Another important stability problem is orthogonal stability,i.e.,Ulam stability problem of orthogonal functional equations.

The orthogonal Cauchy functional equation f(x+y)=f(x)+f(y),x⊥y in which x⊥y is an abstract orthogonally was first investigated by Gudder and Strawther[5].Of course,orthogonal Cauchy equation is not equivalent to the classic Cauchy equation[6].They have different stability results(see[2,7-9]).Gudder and Strawther[5]defined⊥by a system consisting of five axioms.In 1985,Rtz[10]defined a new concept of orthogonality by using more restrictive axioms than of Gudder and Strawther.The concept of the orthogonality in the sense of R¨atz is defined as follows.

Suppose R is the set of all real numbers,X is a real vector space with dimX≥2,the orthogonality⊥is a binary relation on X which satisfies the following four properties:

(O1)Totality of⊥for zero:x⊥0,0⊥x; ∀x∈X,

(O2)Independence:x and y are linearly independent,if x⊥y; ∀x,y∈X{0},

(O3)Homogeneity:if x ⊥ y,then αx ⊥ βy; ∀x,y∈ X,∀α,β ∈ R,

(O4)The Thalesian property:let P is a 2-dimensional subspace of X,x∈P,λ∈[0,+∞),then∃x0∈P such that x⊥x0and

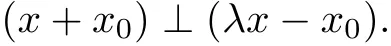
The pair(X,⊥)is called an orthogonality space.

Several orthogonality examples on a real normed space are introduced in[11,12].

Let X be an orthogonality space and Y a real Banach space.A mapping f:X→Y is called orthogonally additive if it satisfies the so-called orthogonally Cauchy functional equation f(x+y)=f(x)+f(y),for all x,y∈X with x⊥y.One of the significant conditional equations is the so-called orthogonal Cauchy functional equation of Pexider type,f(x+y)=g(x)+h(y),x⊥y.

Then many authors discussed the stability problem of orthogonally functional equations.Moslehian[9]considered the stability of the orthogonally Cauchy functional Pexider equation.Park and Rassias[8]considered the stability of the orthogonally Jensen additive functional equations and the orthogonally Jensen quadratic functional equations.Some stability results have been already established for other orthogonally functional equations[13,14].

Recently,Some stability results have been already established for the Cauchy functional equation[15,16],Jensen functional equation[17-19],cubic functional equations[20,21]and other functional equations[22-31]in fuzzy normed spaces,random normed spaces,intuitionistic fuzzy normed spaces,and so on.

Fuzzy normed spaces[32]is defined as follows.

Let X be a real linear space.A function N:X×R→[0,1]is said to be a fuzzy norm on X if for all x,y∈X and all s,t∈R,

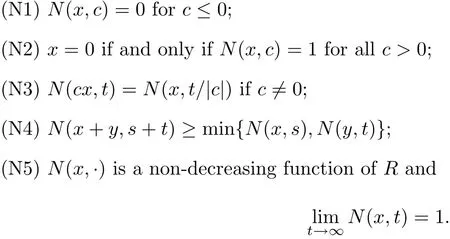
Let(X,N)be a fuzzy normed linear space.A sequence{xn}in X is said to be convergent if there exists x∈X such that limn→∞N(xn−x,t)=1, ∀t>0,then x is the limit of the sequence{xn},denoted by N −limn→∞xn=x.A sequence{xn}in X is called Cauchy if for each ε>0,t>0 there exists n0such that N(xn+p−xn,t)>1−ε for all n ≥ n0,p>0.A fuzzy norm is said to be complete and a fuzzy normed space is called a fuzzy Banach space[15,22,32],if each Cauchy sequence is convergent.

In this paper,we use the notion of a fuzzy normed space given in[32]to exhibit fuzzy stability for orthogonally Cauchy functional equation and orthogonally Cauchy functional Pexider equation in the fuzzy normed linear space setting.

§2. Stability of the Orthogonally Cauchy Functional Equation

First,we prove the stability of the orthogonally Cauchy functional equation in fuzzy Banach spaces for an odd case.

Theorem 2.1 Let(X,⊥)be an orthogonality normed space,f be an odd mapping from X to a fuzzy Banach space(Y,N)such that f(0)=0.Suppose that δ>0 be a positive real number and z0is a fixed vector of a fuzzy normed space(Z,N0)such that

for all x,y∈X with x⊥y,s,t>0.Then there exists a unique additive mapping T:X→Y such that

for all x∈X.

Proof Putting s=t in(2.1),we get

for all x,y∈X with x⊥y,t>0.If x⊥y,then by(O3)x⊥−y.Hence,we can put s=t and replace y by−y in(2.1),we get for all x,y∈X with x⊥y,t>0.Let x∈X be fixed.By(O4)there exists y0∈X such that x⊥y0and x+y0⊥x−y0.Replacing x and y by x+y0and x−y0in(2.3),we have

As limn→∞N0(δz0,2nt/3)=1(x ∈ X,t>0),f(2nx)/(2n)is a Cauchy sequence in fuzzy Banach space(Y,N).Hence,we can define a mapping T:X→Y by

Next,for each n≥1,x∈X and t>0,

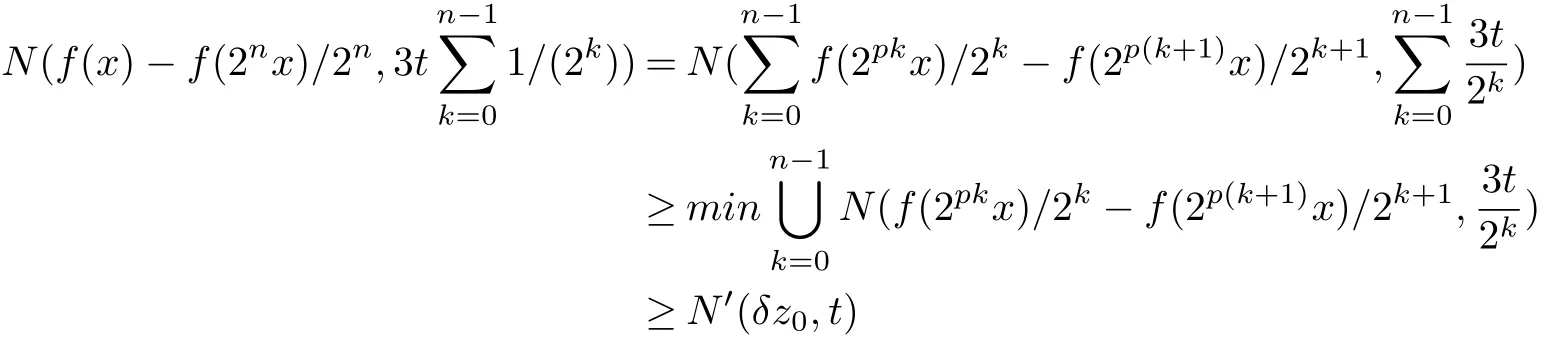
Therefore,For every x∈X and t>0,for large n,we have

for all x,y∈X with x⊥y.The first three terms on the right-hand side of the above inequality tend to 1 as n→∞,and the fourth term is greater than

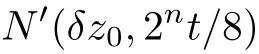
which tends to 1 as n→∞.Therefore

for all x,y∈X with x⊥y.Hence T:X→Y is an additive mapping.Let L:X→Y be another orthogonally additive mapping satisfying(2.2).Then

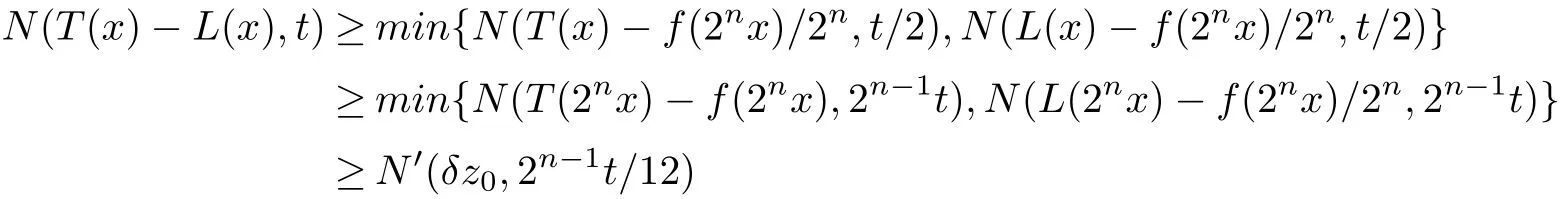
By letting n→∞we obtain

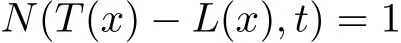
for all x∈X,t>0 and thus the uniqueness of T is proved.

Second,we prove the stability of the orthogonally Cauchy functional equation in fuzzy Banach spaces for an even case.

Theorem 2.2 Let(X,⊥)be an orthogonality normed space,f be an even mapping from X to a fuzzy Banach space(Y,N)such that f(0)=0.Suppose that δ>0 be a positive real number and z0is a fixed vector of a fuzzy normed space(Z,N0)such that

for all x,y∈X with x⊥y,s,t>0.Then there exists a unique additive mapping T:X→Y such that

for all x∈X.

Proof Putting s=t in(2.7),we get

for all x,y∈X with x⊥y,t>0.If x⊥y,then by(O3)x⊥−y.Hence,we can put s=t and replace y by−y in(2.7),we get

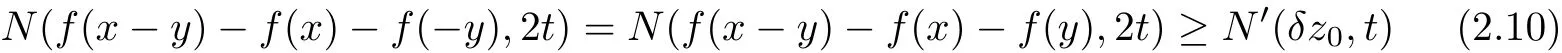
for all x,y∈X with x⊥y,t>0.Let x∈X be fixed.By(O4)there exists y0∈X such that x⊥y0and x+y0⊥x−y0.Replacing x and y by x+y0and x−y0in(2.9),we have

Then by(O3),x+y0/2⊥±(x−y0)/2 and so by using(2.9),we obtain

Using(2.12)and(2.13),we obtain

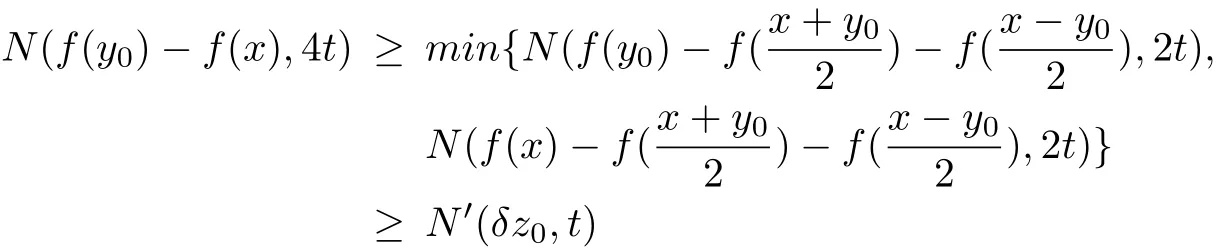
And using(2.9)and(2.10),we obtain

As limn→∞N0(δz0,4n2t/7)=1(x ∈ X,t>0),f(2nx)/(4n)is a Cauchy sequence in fuzzy Banach space(Y,N).Hence,we can define a mapping T:X→Y by

Therefore,For every x∈X and t>0,for large n,we have

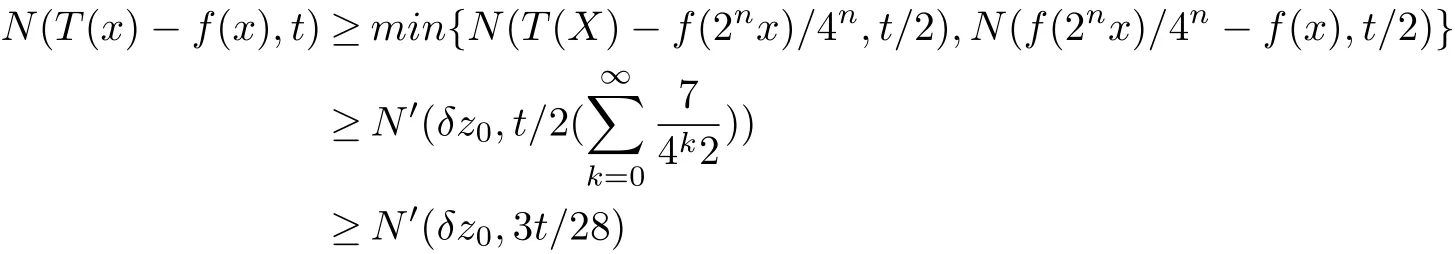
The proof of T is additive is similar to the proof of Theorem 2.1.Also the uniqueness assertion can be proved,the proof is similar to the proof of Theorem 2.1.

§3. Stability of the Orthogonally Cauchy Functional Pexider Equation

First,we prove the stability of the orthogonally Cauchy functional Pexider equation in fuzzy Banach spaces for an odd case.

Theorem 3.1 Let(X,⊥)be an orthogonality normed space,f,g,h be an odd mapping from X to a fuzzy Banach space(Y,N)such that f(0)=g(0)=h(0)=0.Suppose that δ>0 be a positive real number and z0is a fixed vector of a fuzzy normed space(Z,N0)such that

for all x,y∈X with x⊥y,s,t>0.Then there exists a unique additive mapping T:X→Y such that

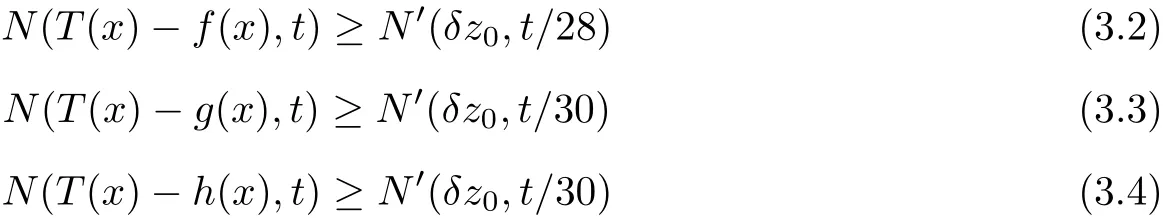
for all x∈X.

Proof Putting y=0,t=s in(3.1),we get

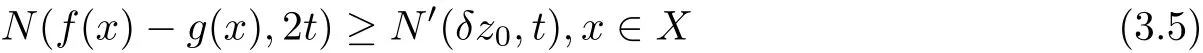
for all x∈X,since x⊥0.So Putting x=0,t=s in(3.1),we get

for all y∈X,since y⊥0.If x⊥y,then by(O3)x⊥−y.Hence,we can put s=t and replace y by−y in(3.3),we get

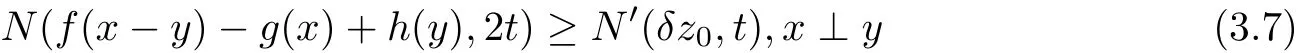
Let x∈X be fixed.By(O4)there exists y0∈X such that x⊥y0and x+y0⊥x−y0.Replacing x and y by x+y0and x−y0and putting s=t in(3.1),we have

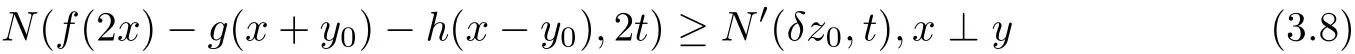
Using(3.5),(3.6)and(3.8),we obtain

As limn→∞N0(δz0,2nt/7)=1(x ∈ X,t>0),f(2nx)/(2n)is a Cauchy sequence in fuzzy Banach space(Y,N).Hence,we can define a mapping T:X→Y by

Therefore,For every x∈X and t>0,for large n,we have

Applying(3.5),we get

Similarly,it follows from(3.6)that T(x):=N −limn→∞h(2nx)/2n.For all x,y∈X with x⊥y,

The first three terms on the right-hand side of the above inequality tend to 1 as n→∞,and the fourth term is greater than

which tends to 1 as n→∞.Therefore

for all x,y∈X with x⊥y.Hence T:X→Y is an additive mapping.Further,

The uniqueness assertion can be proved,the proof is similar to the proof of Theorem 2.1.

Second,we prove the stability of the orthogonally Cauchy functional Pexider equation in fuzzy Banach spaces for an even case.

Theorem 3.2 Let(X,⊥)be an orthogonality normed space,f,g,h be an even mapping from X to a fuzzy Banach space(Y,N)such that f(0)=g(0)=h(0)=0.Suppose that δ>0 be a positive real number and z0is a fixed vector of a fuzzy normed space(Z,N0)such that

for all x,y∈X with x⊥y,s,t>0.Then there exists a unique additive mapping T:X→Y such that

for all x∈X.

Proof The proof is similar to the proof of Theorem 2.1 and Theorem 3.1.

Remark 3.1 In this case,the additive mapping T is defined by

§4. Conclusions

We establish the stability of orthogonal Pexiderized Cauchy functional equation and orthogonal Pexiderized Cauchy functional equation in fuzzy normed space for an odd case,and the stability of orthogonal Pexiderized Cauchy functional equation and orthogonal Pexiderized Cauchy functional equation in fuzzy normed space for an even case.It is easy to see that the fuzzy stability of orthogonally Cauchy additive functional equation is not equivalent to the fuzzy stability of Cauchy additive functional equation(see[15]).This phenomenon may show the significance of study of the fuzzy stability of orthogonal functional equations.