Critical Exercise Price for American Floating Strike Lookback Option in a Mixed Jump-Diffusion Model
2018-12-03YANGZhaoqiang
YANG Zhao-qiang
(Library Special Collections Center and School of Statistics,Lanzhou University of Finance and Economics,Lanzhou 730101,P.R.China)
Abstract:This paper studies the critical exercise price of American floating strike lookback options under the mixed jump-diffusion model.By using Itˆo formula and Wick-Itˆo-Skorohod integral,a new market pricing model established under the environment of mixed jumpdiffusion fractional Brownian motion.The fundamental solutions of stochastic parabolic partial differential equations are estimated under the condition of Merton assumptions.The explicit integral representation of early exercise premium and the critical exercise price are also given,then the American floating strike lookback options factorization formula is obtained,the results is generalized the classical Black-Scholes market pricing model.
Key words:mixed jump-diffusion fractional Brownian motion;Wick-Itˆo-Skorohod integral;market pricing model;option factorization;critical exercise price
§1. Introduction
Let BH={,t≥0}be a fractional Brownian motion(fBm)with arbitrary Hurst parameter H∈(0,1);t∈R with mean E[]=0 and covariance

for all s,t∈ R.Here E denotes the expectation with respect to the probability law for BH(t,ω)and we assume BH(0)=0.

§2.MJD-fBm Pricing Model And Fractional Wick-Itˆo-Skorohod Integral
In this section we construct mixed Poisson jump-diffusion processes as a suitable alternative to fractional Brownian motion.
2.1 MJD-fBm Pricing Model
Suppose an option whose value Vt=V(St,t)depends only on St,t,option pricing formula while the dynamics of stock log-price Stsatisfies

where µ is the instantaneous expected return,σ1and σ2are the instantaneous volatility,and σ1, σ26=(0,0).Assume that Btand BHtare independent.
Lemma 2.1[13]Let Vt=V(St,t)is a binary differential function,if the dynamics of asset price Stsuitable for the mixed fractional stochastic differential equation(2.1),then

Consider a continuous-time financial market in[0,T].It can be described by a filtered complete probability space{Ω,F,Ft,P}.{Ft}0≤t≤Tis a natural σ− filtration generated by a standard Brownian motion Bt,fractional Brownian motionand a Poisson process Pt.Here Ptis an(Ft,P)-Poisson jump process with intensity λ,independent of Btand BtH.jtis jump percent at time t and i.i.d.,jtsatisfy Merton assumptions ln(1+jt)∼N[ln(1+µj)−where µjis the unconditional expectation of jt,andis the variance of ln(1+jt).Notice that the unconditional expectationµjis deterministic and can be calculated,jtis a bounded function of t,so we assume that σ3=ln(1+ µj)is a constant.By Lemma 2.1 we have Lemma 2.2 as follows.
Lemma 2.2 Let Vt=V(St,t)is a binary differential function,if the risky asset Stsuitable for the following mixed jump-diffusion fractional stochastic differential equation

Proof We assume that dPtadmits two-point distribution as following:
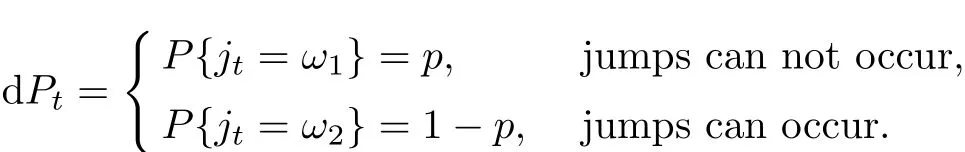
Moreover,during the time interval[t,t+dt],we can write the probability of jumps can not occur as P(ω1)=1 − λdt,the probability of jumps can occur as P(ω2)= λdt.In the case jt>0,St+>Stdescribes stock price Sthas upward jump at time t.In the case jt<0,while St+
Let Πt=Vt− ∇tStis a riskless portfolio and ∇tis stock shares at time t.In a completefinancial markets,there are no risk-free arbitrage opportunities.Thenµ=r and

By model(2.2),in time interval[t,t+dt],the pricing satisfy the following hypothesis:
i)If jumps can not occur,for the events ω1,by Vt=V(St,t)second order differentiable,hence we can use Itˆo formula,then

ii)If jumps can occur,for the events ω2,we have



then under the environment of MJD-fBm,European option pricing model can be expressed as a parabolic integral equation which containing expectation.
Hence we can use Taylor expansion and imitate proof of Lemma 2.1,then by

and approximate that(dBt)2=dt,and(dBHt)2≈ V ar(dBHt)=E(dBHt)2=dt2H=2Ht2H−1dt,using Taylor expansion
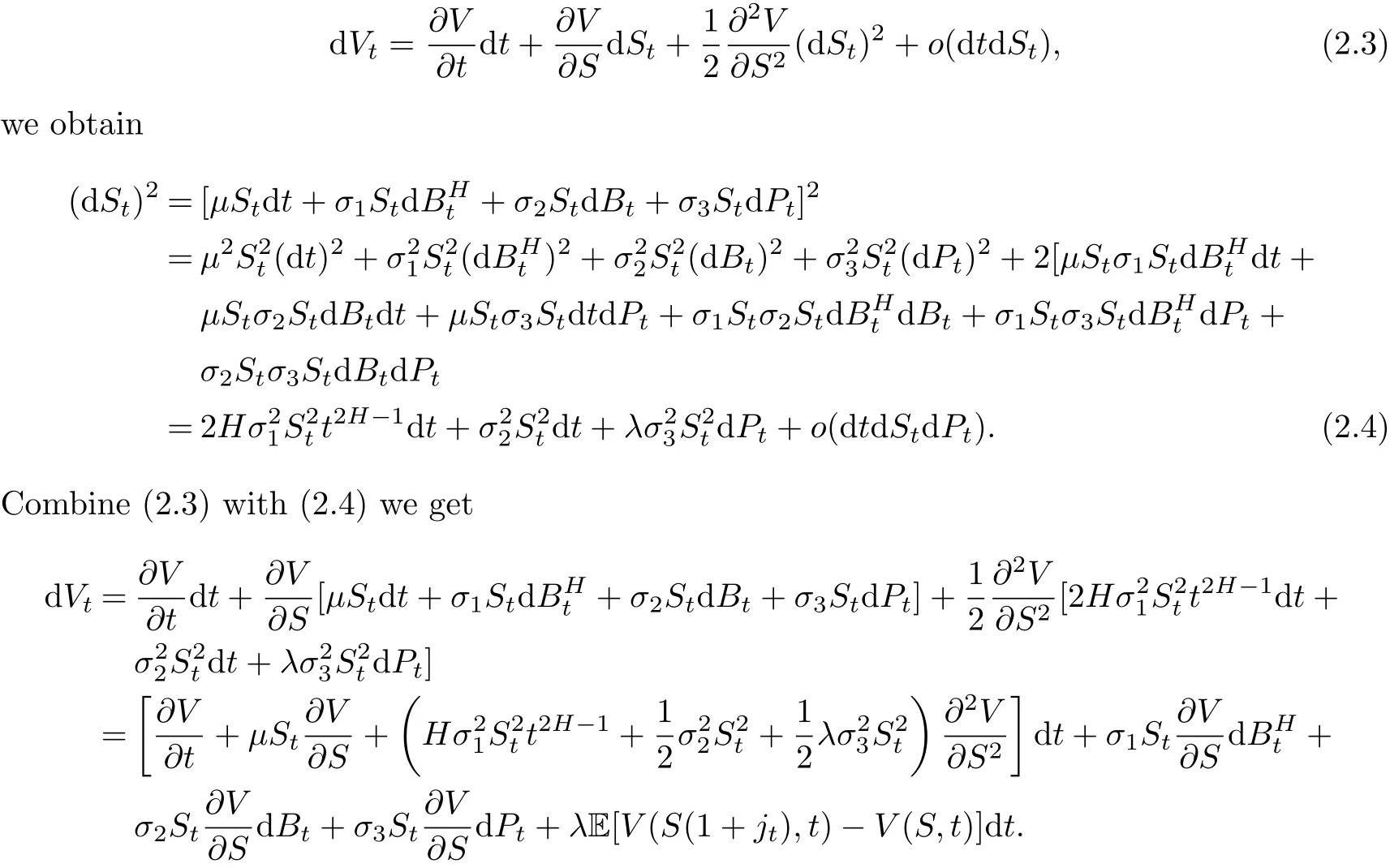
2.2Fractional Wick-Itˆo-Skorohod Integral and Mixed Jump-diffusion Fractional Stochastic Differential Equation
Definition 2.2.1[3]Let Y:R → (δ)∗is a given function,remark thatis the fractional Gaussian noise,andis considered as an element in the Hida space.Define(δ)Hto be the set of all ψ(ω)where(ω)is the Hermite polynomials.Let F(ω)=α∈δaα(ω)and G(ω)=β∈δbβHeβ(ω)be two members of,then we define the Wick product F ƒ G of F and G by

Such that Ytƒis dt-integrable in(δ)∗.Then the fractional Wick-Itˆo-Skorohod integral of Ytwith respect toby

where ƒ is the Wick product andis the fractional Gaussian noise.If X ∈ (δ)∗H,then we define its Wick powers Xƒnby

and we define its Wick exponential expƒ(X)by provided that the series converges in(δ)∗H.

Lemma 2.2.1[3],(FractionalGirsanovformulaI)Let ψ∈Lp(PH),for some p>1 and let γ ∈ L2φ(R)∩C(R) ⊂ δ0(R).Let eγ be defined by eγ =RRφ(t,s)γ(s)ds.Then the map ω→ψ(ω+ eγ)belongs to Lρ(PH),for all ρ
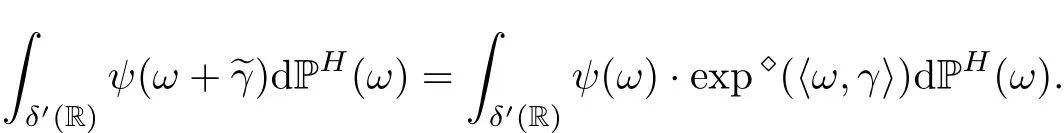
Here δ(R)be the Schwartz space of rapidly decreasing smooth functions on R,and we equip δ(R)with the inner product

Lemma 2.2.1[3],(FractionalGirsanovformulaI)Let T>0,and let γ be a continuous function with supp γ⊂[0,T].Let K be a function with supp K⊂[0,T]and such that
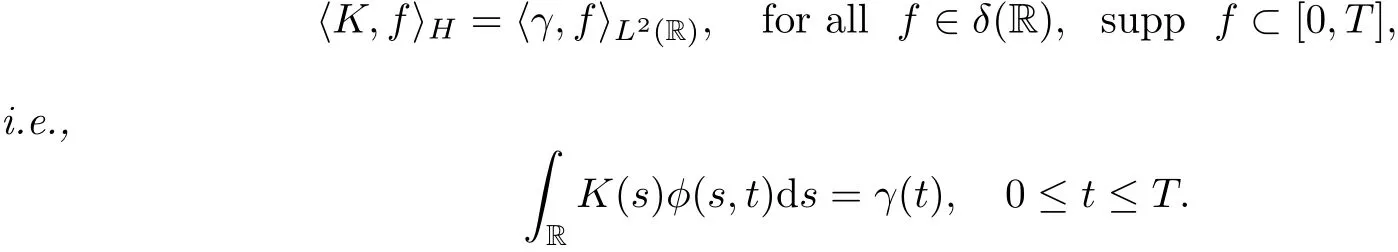
Lemma 2.2.2([3],Wick products on different white noise spaces) Let P=PH,Q=PH,γ,andRds.Let the Wick products corresponding to P and Q be denoted by ƒPand ƒQ,respectively.Then
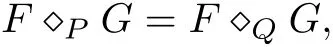
for all F,G ∈ (δ)∗H.
We assume that there are no transaction costs in buying or selling the stocks or options,that is,the market is frictionless and the option can be exercised only at the time of maturity,the market does not admit arbitrage opportunity[3]when H>
Suppose the price of the risky asset Stand interest rate rtsatisfy the following equation

By Definition 2.2.1,Lemma 2.2.1 and Lemma 2.2.2 we can consider the mixed jump-diffusion fractional stochastic differential equation

where r is the instantaneous expected return,q is bonus rates, σ1and σ2are the instantaneous volatility,σ3is the unconditional expectation of jt.Assume that Bt,BtHand Ptare independent.For native assets consecutive dividend payment.
Let J is the path-dependent variable,For lookback put option on the maturity T,the stock price Stis satisfy St≤Jt=for lookback call option on the maturity T,the stock price Stis satisfy St≥Jt=Thus,the lookback put option value V(St,Jt,t)is the function of S,J and t.Then we construct a riskless portfolio Π =V − ∇ ƒ S,select the appropriate variable∇ makes the investment portfolio Π in the interval(t,t+dt)on risk-free.Then dΠ=r(V− ∇ ƒ S)dt,according to the Itoˆ formula we have

Notice that Jtis non-differentiable about t,definesuch that approximate amount Jn(t)is differentiable about t and satisfy

Hence Stis continuous function about t,for n→ ∞,thenwe get

where S≤Jnand E is the expectation operator of V.
For fixed(J,t),when n→∞,thensince we obtain the general equations of European lookback Option under the environment of mixed jump diffusion fractional Brownian motion as follows:

Its financial meaning is clear:the option price is not sensitive to the level of the maximum of the asset price.Therefore the price model for the lookback put option is the terminal-boundary problem(2.5)-(2.7)in the domain{0≤S≤J<∞,0≤t≤T}.
§3.Main Results
In this section we present the factorization formula of the European lookback options and its critical exercise boundary.
3.1 Fundamental Solution Derivation of the General Equations
Define G(S,t;ξ,T)is the fundamental solution of the following solution problem:where 0 Lemma 3.1.1 (see[11]) The price of a derivative on the stock price with a bounded payo fff(St)is given by D(t,St),where D(t,S)is the solution of the PDE: Lemma 3.1.2 The solution of stochastic partial differential equations(3.1)and(3.2)is where Endenotes the expectation operator over the distribution of The solution of stochastic parabolic partial differential equations(3.7)and(3.8)can be written as Combine(3.9)with(3.5)and(3.6)we have Theorem 3.1.3 The fundamental solution G(S,t;ξ,T)consider to be the function of ξ and t,and G(S,t;ξ,T)satisfies the adjoint equation of(3.1)and(3.2).If we note Corollary 3.1.4 By Lemma 3.1.1,Lemma 3.1.2 and Theorem 3.1.3,if we note G∗(ξ,η;S,t)is the fundamental solution of(3.11)and(3.12),then Proof of Theorem 3.1.3 For any†>0,considering integral as follow When x→0,∞,we have The literature[10]introduced a American floating strike lookback call and put option,where the floating strikes and maturity date T are given,respectively,by(ST−mT)+and(MT−ST)+.Given a finite time horizon T>0,let C=C(t,S,M)be the value of the American floating strike lookback call option at time t∈[0,T].Note that the values of American and European call options are equal if the underlying asset pays no dividends.In the absence of arbitrage opportunities,the value C(t,S,m)is a solution of an optimal stopping problem where Ttis a stopping time of the filtration F and the conditional expectation is calculated under the risk-neutral probability measure P.The random variable∈[t,T]is called an optimal stopping time if it gives the supremum value of the right-hand side of(3.13).It is clear from(3.13)that C is nondecreasing in S and nonincreasing in t,m,and a.Solving the optimal stopping problem(3.13)is equivalent to finding the points(t,St,mt)for which early exercise before maturity is optimal.Let be the whole domain,and let E and C denote the exercise region and continuation region,respectively.In terms of the value function C(t,S,m),the exercise region E is defined by for which the optimal stopping time T∗tsatisfies The continuation region C is the complement of S in D,such as The boundary that separates S from C is referred to as the early exercise boundary,which is defined by At the early exercise boundary[¯S(t,m)]t∈[0,T],American floating strike lookback call option would be optimally exercised.In terms of S(t,m),the continuation region C can be represented as Let V(S,J,t)be the lookback option price at time t with stock price S and path-dependent variable J.Using argument similar to Section 2.2,it can be shown that the American floating strike lookback option price solves the following stochastic partial differential equations: where 0≤t≤T,and satisfy an order continuous differentiable on domain the terminal condition is given by We define the differential operator Lt,Sby Then the free boundary problem can be written in a linear complementary form as together with auxiliary conditions For the free boundary[¯S(t,m)]t∈[0,T],this problem is equivalent to solving the Black-Scholes-Merton partial differential equations together with the boundary conditions and the terminal condition In the same way as in the call case,by(3.13)-(3.20),we can formulate the put case:Let P=P(t,S,M)be the value of the American floating strike lookback put option at time t∈[0,T].The value P(t,S,M)is a solution of an optimal stopping problem and P(t,S,M)satisfies the same PDE as(3.18),then where[S (t,M)]t∈[0,T]is the early exercise boundary for put.The boundary conditions for put are and the terminal condition is given by As is known that the value of an American option can be represented as the sum of the value of the corresponding European option and the early exercise premium.For American lookback options,literature[11]proved that the value has such a decomposition and that the premium has an integral representation.Applying the same solution method as in Theorem 3.1.3 to the PDE(3.24)for P(t,S,M),we can obtain the early exercise representation V(t,S,M)under our mixed jump-diffusion fractional Brownian motion environment,which is shown in the following theorem. Theorem 3.3.1 Let V(t,S,M)is American floating strike lookback put option,then where VE(t,S,M)is price of the hedging portfolio of the equivalent European option,and where Endenotes the expectation operator over the distribution ofis contractual strike price,N(·)is the cumulative normal distribution function and e(t,S,M)is early exercise premium,and its explicit integral can be represented by Proof Suppose V(t,S,M)satisfies an order continuous differentiable on domain Σ:Σ={0≤S≤M<∞,0≤t where L is the Black-Scholes operator. Multiplying both sides of the equation(3.30)to G∗(ξ,η;S,t)and quadrature on domain{0≤ξ≤ M<∞,t+†≤ η≤T},For Σ2={0≤ ξ≤M ≤ Sη,0≤ η where L∗is the adjoint Black-Scholes operator,and when ξ→ 0,∞,we have Then the prove is finished. Remark 1 If the critical exercise boundary is given by S=St,then pricing of American floating strike lookback put options can be represented as(3.25)-(3.29). Remark 2 This results show that American floating strike lookback options is equal to the option of a hedging portfolio:a risk premium associated with the European values plus the early-exercise premium.Using the similar techniques,the critical exercise boundary can be given by the following Corollary. Corollary 3.3.2 The critical exercise boundary of American floating strike lookback put options is defined by S=St,0≤t where N(·)is the cumulative normal distribution function and Sη≥ M>0,0< η ≤ T. Proof By(3.29)and Lemma 3.1.2,e(S,t)can be represented by Substituting(3.33)into(3.25),we have then we obtain In practice,it is very difficult to calculate nonlinear integral in(3.31),we only show that this assumption holds in Volterra integral equation for the critical exercise boundary,by the relation(3.31)and Theorem 3.3.1,asymptotic expression of optimal exercise boundary S=Stis obtained near the maturity t=T.Comparing with Theorem 3.3.1 and Corollary 3.3.2,the critical exercise boundary and Volterra integral equation of American floating strike lookback call option are obvious as follows. Corollary 3.3.3 Let V∗(t,S,m)is American floating strike lookback call option,then where Endenotes the expectation operator over the distribution ofis contractual strike price,N(·)is the cumulative normal distribution function and e∗(t,S,m)is early exercise premium,and its explicit integral can be represented by In the whole domain D={(t,S,M)∈ [0,T]×[M,∞)×R+}of the American floating strike lookback put option model,the American put is alive when S As deduced from(3.31),at a given time t,the optimal exercise boundary St(t,S,M)increases linearly with M.Since both S(t,M)and M are increasing function of time t,and so St(t,S,M)increases as time is approaching expiration. Similarly,the critical exercise price for the American floating strike lookback call option should be denote as where S(t,m)is a monotonically decreasing function of time t.The plots of S(t,M)andS(t,m)against time t with varying interest rate are shown in Fig.1,where m=M=100,T=1,r=0.05,q=0.02,0.04,0.06,σ1=0.2,σ2=0.3,σ3=0.0071,λ =2.68.Since lower value of interest rate leads to the loss of the time value of the floating strike price to be smaller when the American floating strike lookback call option is exercised prematurely,then the critical exercise price decreases when the interest rate assumes lower value. The asymptotic behaviors at times close to maturity of the critical exercise prices for the American floating strike lookback put and call options are respectively given by Hence the strike prices of the American floating strike lookback put and call options are set to be MT0and mT0,respectively. Fig.1The Critical Exercise Price for American Floating Strike Lookback Option In this paper,we compounds the Brownian motion,fraction Brownian motion and Poisson process by fractional Wick-Itˆo-Skorohod integral.In our new pricing model,the fundamental solutions of stochastic parabolic partial differential equations are estimated under the condition of Merton assumptions.By solving the free boundary problem and the Black-Scholes-Merton partial differential equations,we characterized the critical exercise price of the American floating strike lookback option at a time to close to expiration and at infinite time to expiration.Since the fundamental solution of stochastic partial differential equations plays an important role in numerical inversion for the put and call case.Then we show that for the American floating strike lookback option values are decomposed into the associated European value plus the early exercise premiums.The numerical simulation of our model is well for asymptotic the early exercise boundary,which have some reference significance to pricing other European options and exotic options.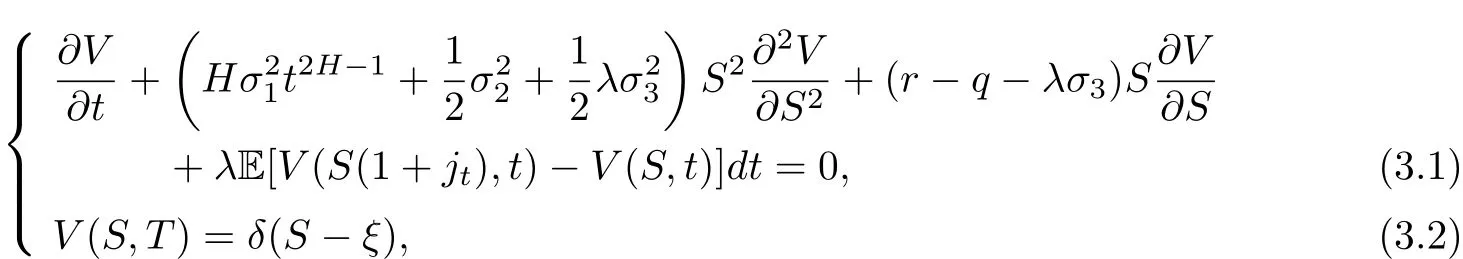


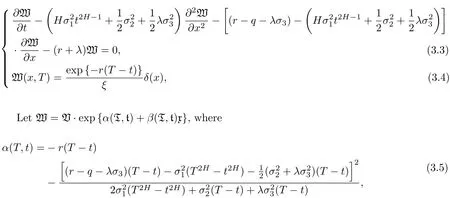





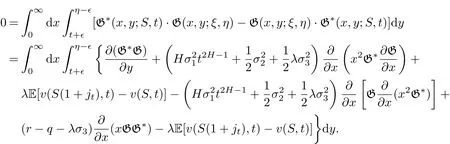

3.2 Early Exercise Boundary of American Floating Strike Lookback Option



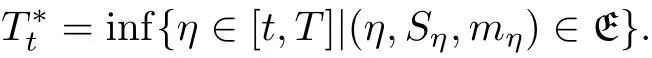





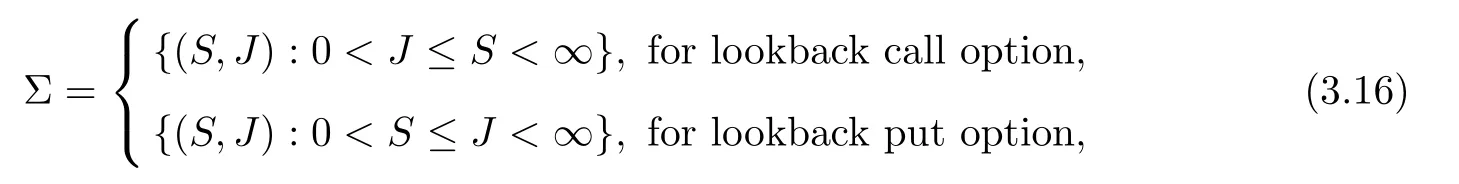

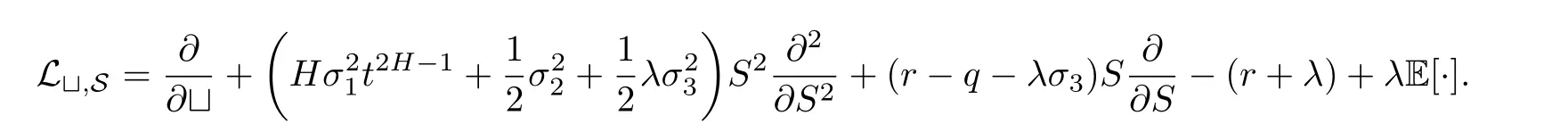
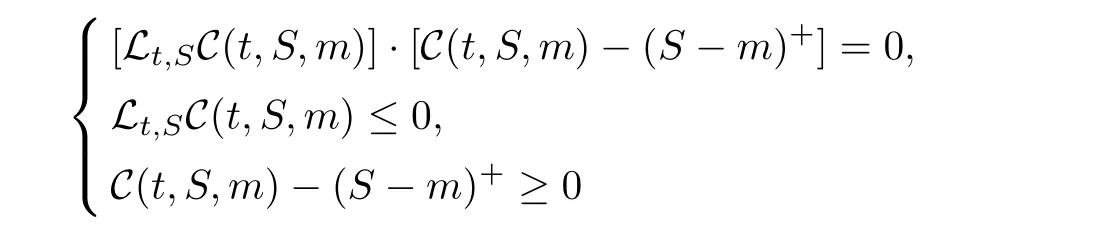








3.3 The Critical Exercise Boundary

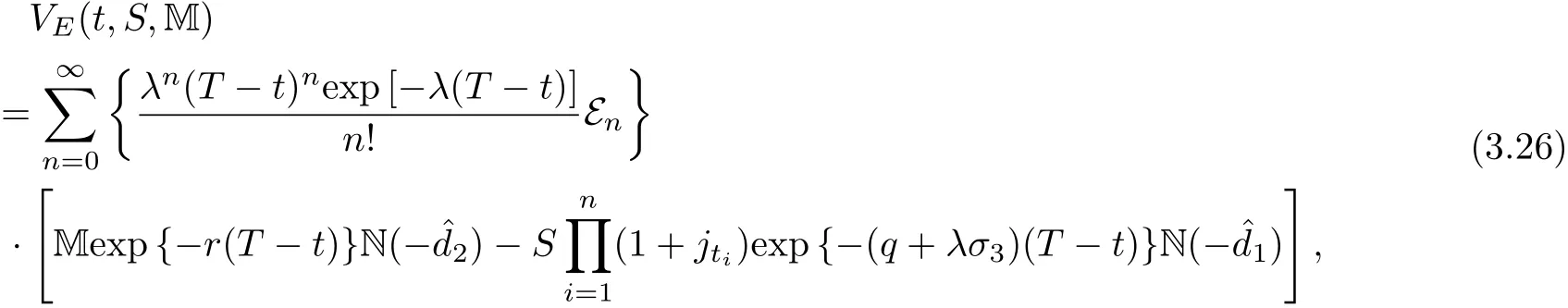



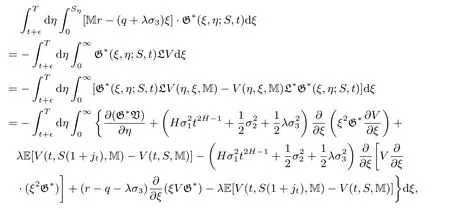









§4.Numerical Simulation





§5. Conclusions
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- The Existence of Domain Wall Solutions in Ambjørn-Nielsen-Olesen Theory
- The Distance Energy of Circulant Graphs
- Strongly α-Reflexive Rings Relative to a Monoid
- Estimation of Derivatives for Bounded Regular Vanishing Functions
- Generalizations of Hermite-Hadamard Type Inequalities Involving S-convex Functions
- The Maschke-type Theorems of Yetter-Drinfeld Hopf Algebras
