带时滞项的高阶Kirchhoff方程的拉回吸引子
2018-12-03徐瑰瑰王利波林国广
徐瑰瑰,王利波,林国广
(1.凯里学院 理学院,贵州 凯里 556011;2.云南大学 数学与统计学院,云南 昆明 650091)
考虑如下带有时滞项的高阶Kirchhoff型方程整体吸引子的存在性:
(1)
方程(1)中m>1,Ω⊂Rn(n≥1)是具有光滑边界∂Ω的有界区域,h>0是时滞时间,φ是当h>0时区间[τ-h,τ]上的初始值;当θ∈[-h,0]时, 定义ut(θ)=u(t+θ),ν是∂Ω上的单位法向量.
Kirchhoff[1]在研究弹力绳的非线性震动时首次提出了Kirchhoff绳模型.随后,Kirchhoff型波方程整体解的存在唯一性以及解的爆破性引起了许多学者的广泛研究.Yang等[2]研究了如下带有强耗散项的Kirchhoff型方程的整体吸引子:
其中x∈Ω,t>0,且
Li等[3]研究了如下带有非线性耗散项的高阶Kirchhoff型方程解的整体存在性和爆破性:
其中Ω⊂RN(N≥1)是具有光滑边界的有界开区域,ν是向外的法向量,m>1是正整数,p,q,r>0是正常数.文中利用凹度方法,得到当p≤r时解具有整体存在性,然而当p>max{r,2q}时,对任何带有负初始能量的初始值,解以Lp+2中的范数在有限时间内爆破.Salim[4]通过修改证明方法,不仅改善了文献[3]的结果,而且证明了当正初始能量有上界的时候,解在有限时间内也爆破.受文献[3-4]的启发,Ye等[5]研究了如下带有阻尼项和源项的高阶Kirchhoff型的双曲方程:
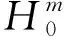
Gao等[6]研究了如下带有非线性强阻尼项的高阶非线性Kirchhoff型方程:
其中m>1是正整数,Ω⊂Rn是具有光滑边界的有界区域,ν是向外的法向量,q>0是正常数,g(u)是非线性函数.通过改善文献[5]中非线性项的假设条件,文献[6]得到了上述方程光滑解的整体存在唯一性,进而得到解半群{S(t)}t≥0具有整体吸引子,最后证明了该整体吸引子具有有限的Hausdorff维数和Fractal维数.
Lin等[7]研究了如下带有强耗散项的高阶非线性Kirchhoff型波方程的解的局部存在性和爆破性:
其中m>1是正整数,Ω⊂Rn是具有光滑边界的有界区域,ν是向外的法向量,a≥0,b≥0,p≥0,q≥1是常数.
由于时滞偏微分方程带有对过去状态的刻画,能够更精确地反映现实,因而时滞偏微分方程的研究也吸引了越来越多学者的注意[8-12].目前,关于高阶Kirchhoff型方程的研究主要集中在解的爆破及其存在性,对带有时滞的高阶Kirchhoff型方程的研究鲜见报道.拉回吸引子是相空间的一族紧集,在过程的作用下具有不变性,且拉回吸引相空间中的有界集.从存在性角度考虑,相对一致吸引子而言,可以在较弱的外力假设下得到拉回吸引子的存在性.因此,研究带有时滞项的高阶Kirchhoff型方程的拉回吸引子是十分有意义的.
1 预备知识
为了后面证明的需要,首先引入以下符号:
H=L2(Ω)中的范数与内积分别记作·和(·,·),且记

(H1)对∀ξ∈R,h(ξ)是连续的;
(H2)h(0)=0;
(H3)存在一个常数Lh>0,使得对任意的ξ,η∈R,有h(t,ξ)-h(t,η)≤Lhξ-η;
(H4)存在常数m0>0,Ch>0,使得对任意的m∈[0,m0],t≥τ,u,v∈C0([τ-r,τ],H),有

1)U(t,τ)=U(t,r)U(r,τ),∀τ≤r≤t;
2)U(τ,τ)=I为恒同算子,τ∈R.
则称U(t,τ)是一个过程.
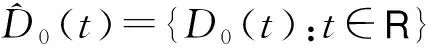
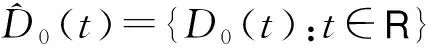

∀t∈R.
定理1[9](Poincare不等式) 若Ω⊂Rn是有界开子集,则
2 拉回吸引子的存在性
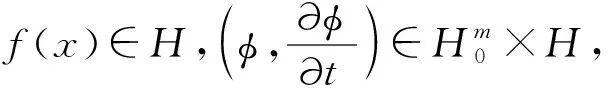

λ1是-Δ在H中的第一个特征值,而

用v与问题(1)中的第一个方程在H中作内积,可得
对(4)式逐项进行计算,有
把(5)~(7)式代入(4)式,可得
而由Young不等式及Poincare不等式可得
其中λ1是-Δ在H中的第一个特征值.
由f(x)∈H及Young不等式可得
把(9)~(12)式代入(8)式,可得
由Young不等式可得
(14)
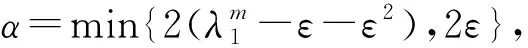
其中
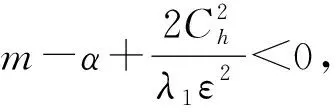
在[τ,t]上对上式积分,有
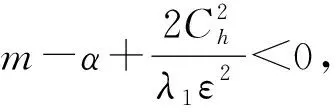
由广义Young不等式可知
因而由(16)式可得
用t+θ(-h<θ<0)代替上式中的t,则有
从而定理中的(2)式得证.
因此存在常数E0>0和t0>τ,使得当t≥t0时,有
从而定理中的(3)式得证. 】
定理3若条件(H1)~(H4)成立且
其中
因而存在常数E1>0和t1>τ,使得当t>t1时有

对(17)式逐项进行计算,有
由Young不等式及Poincare不等式可得
其中λ1是-Δ在H中的第一个特征值.
把(18)~(23)式代入(17)式,有
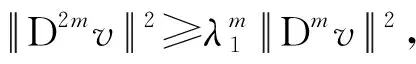
由定理2可知,Dmu2-ε>0,由于
所以

在[τ,t]上,对(26)式利用Gronwall不等式,可得

Dmφ2e(2ε-C)(t-τ)→0,
因而
由定理2可知,Dmu2是有界的,这表明(26)式成立,则(25)式可以变形为
其中
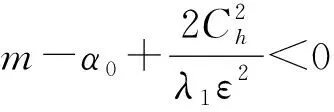
对上式在[τ,t]上积分,有
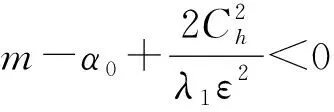
设α1=min{1,Dmu2-ε},则
用t+θ(-h<θ<0)代替上式中的t,则有
因而存在常数E1>0和t1>τ,使得当t≥t1时,有
从而定理得证. 】
定理4若条件(H1)~(H4)成立,且

证明由Fadeo-Galerkin方法以及定理2和定理3可得初边值问题(1)的光滑解的存在性,下面证明解的唯一性.
设u1,u2是问题(1)的两个解,φ,φ是相应的初值,记ω=u1-u2,当t∈[τ-h,τ]时,
于是

对(29)式逐项进行处理,可得
把(30)~(33)式代入到(29)式,可得
由定理2,定理3,Lagrange中值定理以及绝对值不等式可得

由条件(H3)可得
利用(35),(36)式及定理2,可将(34)式变形为
其中
在[τ,t]上对(37)式使用Gronwall不等式,可得

即
于是
即
ω(x,t)=0.
所以当初值相同时,u1=u2,从而得到了解的唯一性. 】