GNSS/SINS松组合系统的可观测性分析

肖佳敏，朱 锋，张小红

(武汉大学 测绘学院，武汉 430079)

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)与捷联式惯性导航系统(strapdown inertial navigation system，SINS)功能互补，二者组合之后具有导航精度高、可靠性好等特点，广泛应用于海陆空各领域的导航。GNSS/SINS松组合系统一般采用卡尔曼滤波，对系统进行可观测性分析有利于了解卡尔曼滤波性能，认识系统参数与状态量估计之间的关系。松组合系统在特定情况下并非所有状态量都是可观测的，对不可观测的状态量进行滤波难以得到准确的估计结果。根据可观测性分析结果，载体进行一定机动可以使得某些误差状态由不可观测变为可观测，为系统实现快速收敛提供参考，因此在工程实践中有必要考虑组合导航系统的可观测性。

由于载体运动，松组合系统为时变系统，滤波过程中状态量的可观测性不会一成不变，使得时变系统的可观测性分析变得困难。文献[1-2]提出了分段定常系统(piece-wise constant system，PWCS)可观测性理论，将时变系统视为短时间内的定常系统，通过求系统的提取可观测性矩阵(stripped observability matrix，SOM)简化了对时变系统可观测性的分析。基于PWCS可观测性理论，国内外学者对导航系统的可观测性进行了研究。文献[2]分析了惯导系统飞行对准时，线运动对于提高误差状态可观测性的作用。文献[3]分析了地心地固系(e系)下，具有杆臂误差的GPS/INS组合导航系统的可观测性。文献[4]分开考虑了系统的可观测部分与不可观测部分，对系统状态量进行逐个分析。文献[5]利用状态方程解耦的思想降低了系统SOM的复杂度，并给出误差状态可观测性与载体线运动、角运动之间的联系。

e系下的松组合滤波模型中姿态误差表示在载体系下，减少了后续可观测性分析的工作[6]。但实际中对载体而言e系下运动方向不明，不便于对载体机动进行确切的指导以达到提高状态量可观测性的目的，而当地水平坐标系(n系)物理意义明确，对载体而言操作更加方便。本文选取n系作为参考系，根据实际中导航参数的数值范围对滤波系统进行了简化，接着利用PWCS理论求得系统的SOM，通过对状态量进行解耦分析了杆臂误差与位置误差、姿态误差与加计零偏的可观测性，并得到了杆臂误差、姿态误差以及加计零偏的可观测性与载体运动之间的联系，最后通过仿真对结论进行了验证。理论分析与仿真测试证明了载体运动可以使得系统状态量由不可观测变为可观测，从而提高状态量的估计速度及精度，对工程实践有指导意义。

1 18维状态的松组合数学模型

本文采用n系下的GNSS/SINS松组合模型作为可观测性分析的对象，建立了18维状态的系统状态模型，包括位置误差δrn、速度误差δvn、失准角φ、加计零偏ab、陀螺零偏εb和杆臂误差δlb。在不考虑系统噪声的情况下，n系下松组合的系统状态方程[7-8]为

(1)

同样不考虑观测噪声的情况下，松组合观测方程[7,9]为

(2)

式中：Z为观测向量；Ln为杆臂值。

由于系统状态方程式中的系数矩阵F十分复杂，不利于后续可观测性矩阵的计算，因此，做如下模型简化：在组合导航实际应用中，一般载体运动速度在100m/s以内，而地球半径数量级达到1×106m，因此矩阵F的子矩阵Frr最大在1×10-4数量级，而惯导系统中位置误差δrn在1×10-3数量级左右，二者乘积远小于速度误差δvn数量级1×10-4对于位置误差微分的影响，因此，位置误差微分方程可以简化[4]为

(3)

同理，子矩阵Fvr、Fvv、Fφr、Fφv数量级均较小，对相应状态量的影响可以忽略，简化后的系统状态方程为

(4)

2 n系下的可观测性矩阵

组合导航系统为连续时变系统，不能直接利用可观测性矩阵来分析。但根据PWCS可观测性分析理论，在短时间内，可以认为系统是时不变的。由式(2)、式(4)，计算系统在第j个时间间隔内的SOM[1]为

(5)

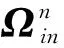
对式(5)进行行变换后得到

(6)

矩阵维数为54×18，式中矩阵4行以下为42×18的零阵。

(7)

3 可观测性分析

根据式中非零阵元素的分布，可以发现位置误差与杆臂误差相互耦合，与其余4种误差解耦。速度误差可观测，载体姿态误差与加计零偏、陀螺零偏耦合。

3.1 位置误差与杆臂误差的可观测性分析

根据式(7)，由PWCS可观测性理论可以得到表示位置误差及杆臂误差的可观测性矩阵为

(8)

式中下标16表示位置误差与杆臂误差在状态量中的位置。

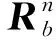
具体考虑2个时间段内的可观测性矩阵。假设开始时载体处于静止状态，2个时间段内的可观测性矩阵为

(9)

(10)

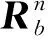
因此有结论1：位置误差与杆臂误差耦合在一起，载体的角运动将提高杆臂误差的估计，而直线运动对于杆臂误差的可观测性没有贡献。载体绕某方向的角速度将使得垂直于该方向的杆臂误差可观测。

3.2 姿态误差、加计零偏与陀螺零偏的可观测性分析

根据式(7)，由PWCS可观测性理论可以得到表示姿态误差、加计零偏及陀螺零偏的可观测性矩阵

(11)

式(11)经行变换后可以拆分成

(12)

(13)

式中：Q34表示姿态误差与加计零偏的可观测性矩阵；Q35表示姿态误差与陀螺零偏的可观测性矩阵。

观察矩阵Q34、Q35，可以发现这3种误差的可观测性与载体的直线运动、角运动均有关系。矩阵Q35中含有n系相对于惯性系的角速度，载体不可控，下面仅对矩阵Q34进行分析，考虑载体分别进行线运动及角运动。

1)载体线运动

(14)

(15)

现考虑2个时间段内的可观测性，开始时载体处于静止状态下，且载体天向与导航系U向保持一致，则可观测性矩阵为

(16)

由于载体静止，有

(17)

式中g为重力加速度。

因此，式(16)可以展开为

(18)

式(18)第3行非零项对应az(天向加计零偏)，也就是说静止时有az可观测。假设载体下一时间段Fb发生改变，例如载体向前加速，有fx=0,fy≠0,fz=g，因此2个时间段的可观测性矩阵为

(19)

因此有结论2：载体在某一水平方向上进行加速运动，将提高该方向上加计零偏的可观测性。直线运动时，姿态误差的可观测性与水平向加计零偏的可观测性耦合，而与天向加计零偏的可观测性解耦。

2)载体角运动

(20)

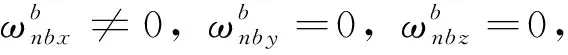
(21)

4 仿真验证

利用仿真数据对上述3条结论进行验证。

分别设计3个实验：实验一确定静止状态下可观测的状态量，仿真静止800 s，滤波初始状态量均为0。实验二，载体先静止100 s，接着以1 m/s2向前加速10 s，然后保持10 m/s的速度匀速向北向运动。整个过程中只有北向速度发生了变化。实验三，载体先静止100 s，接着以1 m/s2向前加速10 s，然后保持10 m/s的速度匀速向北向运动，100 s之后以2°/s的速度向左转90° ，朝西运动100 s最后以2 m/s2减速至0。

根据卡尔曼滤波方差的收敛速度可以判断状态量的可观测度[10]，若其滤波方差未收敛，则说明该状态量不可观测，滤波方差收敛越快，说明状态量可观测度越高。仿真结果分析如下。

图2为姿态误差的滤波结果，图3为加计零偏的滤波结果。实验一中，载体静止时右向及前向姿态误差收敛，而天向姿态误差可观测性较差。由图3(a)、图3(b)可以看到静止时右向及前向加计零偏滤波STD为9.8×10-4m/s2，且没有收敛趋势，完全不可观测，而图3(c)中天向加计零偏可观测。实验二中，100 s后载体向前加速，将提高前向(y向)加计零偏的可观测性，图3(e)显示y向加计零偏STD在100 s后开始收敛，但收敛趋势不明显，说明可观测性仍很差。但此时图3(d)中x向加计零偏依旧不可观测，说明载体的前向加速运动可以提高前向加计零偏的可观测性。同时载体直线运动时，姿态误差的可观测性与水平方向上的加计零偏耦合，实验二中100 s后前向加计零偏可观测性的提高也将提高天向姿态误差的可观测性，图2(f)显示实验二中100 s后天向姿态误差STD收敛加快。验证了结论2。

实验三中210 s后载体天向角速度发生变化，将提高水平向加计零偏的可观测性，图3(g)、图3(h)显示水平向加计零偏在210 s后收敛至0，验证了结论3。

5 结束语

本文研究了n系下GNSS/SINS松组合滤波状态参数的可观测性，包括杆臂误差、姿态误差以及加计零偏。通过分析3种状态参数的可观测性与载体角运动、线运动之间的关系，得到了以下3条结论：1)位置误差与杆臂误差耦合，载体的角运动将提高杆臂误差的估计，而直线运动对于杆臂误差的可观测性没有贡献，载体绕某方向的角速度将使得垂直于该方向上的杆臂误差可观测；2)载体在某一水平方向上进行加速运动将提高该方向上加计零偏的可观测性，直线运动时姿态误差与水平方向的加计零偏耦合，而与天向加计零偏解耦；3)载体只进行角运动时，绕某方向的角运动将使得垂直于该方向上的加计零偏可观测。最后通过仿真实验，验证了本文的可观测性分析结论。工程实践中，在组合导航初始对准阶段，进行加速及转弯，可以加快滤波状态量的收敛速度，快速实现高精度导航定位。