基于分类规则算法对存款意愿倾向的研究
2018-12-01新疆财经大学乌鲁木齐市830012吴珍珍
(新疆财经大学,乌鲁木齐市,830012) 吴珍珍
关键字 J48(C4.5)算法;Naïve Bayes算法;对比分析
分类是数据挖掘中一项非常重要的任务,在现实生活中有非常广泛的应用。例如,根据某一天的天气状况判断这一天是否适合出门游玩;根据病人各项检查指标判断是否患有某种疾病;根据电子邮件的标题和内容判断其是否为垃圾邮件等,以上这些实例都体现出了分类的重要性。
而构造分类器的方法有很多,常见的方法有决策树、规则归纳、贝叶斯学习、神经网络、支持向量机以及Ensemble方法等。在这些方法中决策树因为其易理解、效率较高的优点占有重要的地位,其中作为决策树方法中经典算法的ID3算法的改进算法C4.5能够有效地揭示需要进行分类数据的结构化信息。除此之外,朴素贝叶斯方法因为其对不确定知识表达形式的特别以及综合了先验知识的优质特性成为一种简单高效的分类算法,在数据挖掘中应用广泛。
1 数据挖掘分类规则的基础理论
构造分类器的方法有很多,这里主要对决策树方法中的ID3改进算法C4.5以及朴素贝叶斯算法的基础理论和其算法基本原理作简要介绍。
1.1 C4.5算法基本原理
ID3算法是由罗斯昆(J.Ross Quinlan)于1975年在悉尼大学提出的一种分类预测算法。该算法以信息论为基础,其核心是“信息熵”,通过计算每个属性的信息增益,认为信息增益高的是好的属性,每次划分选取信息增益最高的属性作为划分标准,并重复这个过程,最后实现对数据的归纳分类,生成一个能够完美分类训练集的决策树。
设D是一个包含|D|个数据样本的集合,C为分类属性,|C|为分类类别数目,A为一个属性,Da为D中满足条件A=a的样本集合,PD(Ci)和分别表示D和Da中属于类别C(ii=1,2,…,|C|)的样本数所占百分比。那么由信息熵的定义得出样本集合D对于的信息熵为:

利用属性A对样本集合D中进行划分所对应的信息熵为:
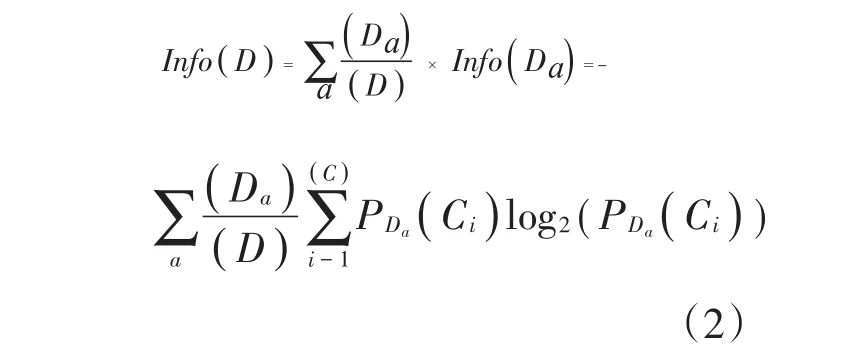
因此,属性A在样本集合D中为分类所提供的信息量即信息增益为:

而C4.5算法是由罗斯昆(J.Ross Quinlan)提出的对ID3算法的一个改进算法,它继承了ID3算法的优点,并且利用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多属性的不足,且在构造决策树的过程中能对其进行剪枝,使得产生的分类规则易于理解,准确率较高。
C4.5算法利用增益比率来克服ID3算法用信息增益选择属性偏向选择取值多的属性作为决策树树根的问题,那么就有:

因此,属性A在样本集合D中为分类所提供的信息量占比即信息增益率为:

一般情况下认为信息增益率高的是好的属性,每次划分选取信息增益率最高的属性为划分标准,并重复这个过程,直至生成一个能够完美分类训练集的决策树。
1.2 朴素贝叶斯方法基本原理
朴素贝叶斯方法是基于贝叶斯定理与特征条件独立假设的一种分类方法,故有这种方法构造的贝叶斯分类器基于一个简单的假定,即给定目标值时属性之间相互条件独立。和决策树相比,朴素贝叶斯方法构造分类器发源于古典数学理论,有更加坚实的数学基础,以及更稳定的分类效率。
设为最大可能后验概率,D是一个包含|D|个数据样本的集合,V为假设空间,为假设H的事前概率,为D的事前概率,这对于假设H而言是一个常数定值,假设H在样本集D下出现的条件概率。那么朴素贝叶斯算法根据贝叶斯定理,在基于给定目标值时属性之间相互条件独立的简单假设前提下,来预测属性分类的结果就有:

假设样本集D有n个属性,记为A1,A2,…,An,其对应的属性值记为a1,a2,…,an;C为分类属性,|C|为分类类别数目。并且可以预测样本D属于类Ci当且仅当有p( Ci|D )>p(Cj|D ),其中i≠j,且i,j=1,2,…,|C|。
而根据贝叶斯定理可以得到p(C i|D )=,这里p(D)对于所有类均为常数,故只需要最大化p( D|Ci)p(Ci)即可。如果所属类别的先验概率p(Ci)未知,则通常假设p(Ci)=p( Cj),这里≠j,且i,j=1,2,…,|C|,所以在给定目标值时属性之间相互条件独立的假设前提下有p( D|Ci)=,从而得出样本D应属类别。
2 基于C4.5及朴素贝叶斯算法的实例解析
Bank Matketing Data Set中共有4 119条数据,其中规定其含有训练数据集2 719条,测试数据集1 400条,分类的目标属性为存款(定期)意愿,记为y。根据年龄(age)、工作类型(job)、婚姻状况(marital)、教育程度(education)、拖欠款状况(default)、房贷(housing)、个人贷(loan)等属性来判断其存款倾向(y)是否有意愿。
在进行分析之前,由于weka部分分类分析算法要求属性必须是nominal类型,故需要将数据集中原本是numeric类型的属性进行离散化,将其转换成nominal类型,例如年龄(age)属性我们定义小于等于20的记为“young”,大于50的记为“old”,大于20且小于等于50的记为“wrinkly”,从而完成了数据的转换。(详见表1)
2.1 算法分类结果将数据集
以.csv的格式导入weka软件中去,使用J48(C4.5)以及朴素贝叶斯等三种分类算法对该数据集进行分类。(详见表2)
从分类结果中可以看出,Naïve Bayes算法的分类效果在准确率与误差率上要比J48(C4.5)算法有微小优势差距,且其算法分类所需要的时间也要比J48(C4.5)算法有着较明显的优势。
2.2 算法分类结果分析
2.2.1 J48(C4.5)算法结果分析
根据weka软件运行结果,J48(C4.5)算法具体分类结果(即Confusion Matrix)见表3。从表3可知,没有存定期款倾向意愿且分类结果也将其划分为没有意愿的实例个数为1 238个;没有存定期款倾向意愿但分类结果将其划分为有意愿的实例个数为0个;有存定期款倾向意愿且分类结果也将其划分为有意愿的实例个数为0个;有存定期款倾向意愿但分类结果将其划分为没有意愿的实例个数为162个。

表1 部分数据集情况

表2 不同算法针对Bank Marketing数据集的分类结果

表3 J48(C4.5)算法对Bank Marketing数据集的分类结果

表4 J48(C4.5)算法在对Bank Marketing数据集的分类效果

表5 J48(C4.5)置信因子调节对分类精度的影响情况
由上,分类正确的实例个数为1 238个,分类错误的实例个数为162个。所以分类的准确率为88.4286%,分类的错误率为11.5 714%。下面再给出J48(C4.5)算法分类的正确率、召回率和F-measure指标的值,结果如表4所示。
由表4可知,正确率(Precision)表示实际上存定期款倾向真实有意愿(真实没意愿)的实例个数占分类成有存定期款倾向意愿(没意愿)的实例个数的比例;召回率(Recall)表示正确分类成有存定期款意愿(没有存定期款意愿)的实例个数占总的有存定期款意愿(没有存定期款意愿)的实例个数的比例;F-measure指标则将正确率与召回率结合起来,揭示两者间的关系,衡量两者的平衡性能,且一般情况下,计算F-measure有公式:
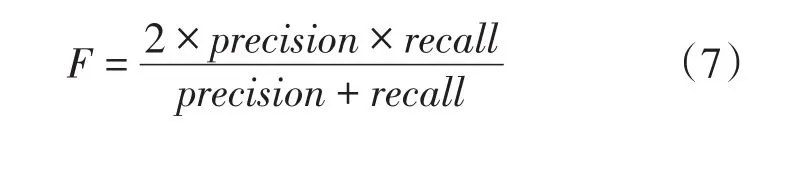
综上,作为ID3算法改进的J48(C4.5)算法,在对Bank Marketing数据集的分类预测中,J48(C4.5)的准确率达到了88.4 286%,分类的速度为0.03秒,它增加了树枝的修剪,克服了关于数据缺失和噪音数据的缺点,该算法应用在该数据集上所得的结果是可以接受的。但是,weka中J48(C4.5)算法有置信因子及新分类的叶子节点上需要含有的实例个数这两个参数可以调节。调节其中一个参数:置信因子,此时得到的分类结果如下表5所示:
由表3~5,可以得到:随着置信因子的增加,J48算法的运行速度、正确率都有所上升,这主要是因为置信因子的增加将减少对树的修剪,从而获得一棵更加特殊的树。
2.2.2 Naïve Bayes算法结果分析
根据weka软件运行结果,Naïve Bayes算法具体分类结果(即Confusion Matrix)如表6所示:
从表6中,可以得到:没有存定期款倾向意愿且分类结果也将其划分为没有意愿的实例个数为1 227个;没有存定期款倾向意愿但分类结果将其划分为有意愿的实例个数为11个;有存定期款倾向意愿且分类结果也将其划分为有意愿的实例个数为0个;有存定期款倾向意愿但分类结果将其划分为没有意愿的实例个数为150个。

表6 Naïve Bayes算法对Bank Marketing数据集的分类结果

表7 Naïve Bayes算法在对Bank Marketing数据集的分类效果

表8 Bank Marketing数据集上不同算法的比较情况
由上,分类正确的实例个数为1239个,分类错误的实例个数为161个。所以分类的准确率为88.5%,分类的错误率为11.5%。下面再给出Naïve Bayes算法分类的正确率、召回率和F-measure指标的值,结果如表7所示。
2.3 J48(C4.5)与Naïve Bayes算法结果的比较分析
数据挖掘中算法的性能比较一般可以从以下几个方面,包括分类速度、准确率、可伸缩性、强壮性以及可理解性等进行比较。可伸缩性表示对于数据量很大的数据集能有效构造模型的能力,朴素贝叶斯算法因其独特的特质对数据量极大且数据集样本属性之间关联尽量小的数据集进行分类的效果具有很大的优势;强壮性表示模型对噪声数据或空缺值数据正确预测的能力,从对基础理论的介绍中我们已经知道了J48(C4.5)算法对这方面的处理更好。因此,表8对所采用的算法进行了一个简单的比较。
由表8可以得到,Naïve Bayes算法相较J48(C4.5)算法不仅分类速度更快,对数据集分类的准确率也更优胜一筹。除此之外,对于样本空间容量巨大的数据集也能够比较有效的进行分类,虽然其对数据值缺失及噪音数据等问题的处理能力比不上J48(C4.5)算法,但在缺失数据量不大的情况下,对由于数据值缺失及噪音数据所引起的问题是可以容忍的。因此,可以得出朴素贝叶斯Naïve Bayes算法要比J48(C4.5)算法的分类效果更好。
3 总结
随着信息化步伐的加快,面对庞杂的数据,如何提取出这些数据中未知的且具有潜在价值的信息就显得尤为重要。利用数据挖掘技术对有用知识进行提取能够为人类提供有决策意义的信息。在介绍数据挖掘中分类技术基础理论的基础上,基于weka平台,利用分类算法中的J48(C4.5)及Naïve Bayes算法对Bank Marketing数据集进行分类实验分析,并从运行速度、正确率、可伸缩性、强壮性等方面对两种算法的分类效果进行了对比分析,得出了Naïve Bayes算法相较J48(C4.5)算法能得到更有效的分类结果的结论。这为银行在对客户相关信息的了解基础上判断该客户是否具有存定期存款倾向的意愿具有重要意义,从而有针对性的增加意愿存定期款客户数量,提高该银行在银行市场的竞争力。
