改进型随机斑块饱和模型及其在致密气层检测中的应用
2018-11-30杨志芳晏信飞卢明辉李晓明
未 晛 杨志芳 晏信飞 卢明辉 李晓明 任 岩
(①中国石油勘探开发研究院,北京 100083; ②北京劳动保障职业学院,北京 100083)
1 引言
致密砂岩储层具有孔渗低、非均质性强,油气水分异性差、分布复杂的特征[1]。特别是水气两相流体饱和时,水气比例及其分布显著影响岩石弹性性质[2],弹性参数与储层参数关系极为复杂[3,4],利用地震资料定量解释多解性强。因此准确刻画饱和度、流体分布对弹性参数的影响成为致密砂岩储层预测或流体检测的研究重点[5-9]。
岩石物理模型能够刻画岩石弹性参数与储层参数之间的关系,是分析岩石物性、含流体性对弹性参数影响的重要工具之一[10]。由于地下储层孔隙中总有一部分水附着于岩石颗粒表面或封闭于某些连通性很差的孔隙空间中,气藏中水气两相部分饱和是地下最常见的状态[6],水气在孔隙中常呈现离散、不规则斑块状分布[11]。对部分饱和储层的岩石物理模型研究,White[12]最先建立了一种外层为规则水壳、内部包含气泡的水气两相部分饱和孔隙模型,展示了部分饱和对介质弹性参数的影响。其后,Dutta等[13]、Johnson[14]和杨志芳等[15]分别对White模型的低频极限、孔隙形状假设及流体分布假设进行了完善或扩展。考虑到更为复杂的介质情况,Pride等[16,17]提出了双孔—双渗模型,产生与Johnson模型相类似的模拟结果。巴晶等[18]基于Biot-Rayleigh波动方程进一步将双孔介质理论模型发展到包含不同流相和固相的部分饱和孔隙介质理论模型。Sun等[19]考虑介观尺度下岩石骨架和孔隙流体分布的非均质性特征,提出了饱和两相流体的双孔介质三层斑块模型,该模型在描述高频全饱和实验数据时具有优势。这些方法在某种意义上都假设孔隙流体具有某些规则形状和尺度(如一定半径球体),赋存于岩石中,而实际介质的物性条件决定了孔隙流体绝大多数不具有规则形状和尺度,最新微观成像结果也可以证明这一特点[11,20]。为了更客观模拟孔隙流体在岩石中的分布,Gurevich等[21]首次提出了一维随机分布的流体非均匀饱和孔隙介质模型。其后,Müller等[22-24]改进了一维随机斑块饱和模型,提出了一种普适的三维随机孔隙介质模型。Toms等[4,25]利用该模型研究了随机斑块饱和介质地震波衰减问题。未晛[26]修正了模型有限性造成的误差并优化了模型参数的给定方式,利用改进型随机斑块饱和模型研究了岩石物性、孔隙流体对岩石弹性参数的影响。随机斑块饱和模型在刻画孔隙流体在岩石中的分布方面具有优势,更贴近真实情况。
基于岩石物理模型,Avseth等[27]提出了AI—VP/VS岩石物理图板技术(RPT),用地震弹性反演结果定量预测孔隙度、饱和度,在实际应用中得到广泛认可,并获得迅速发展。Cao等[28]在岩心测试、测井资料及地震地质综合研究基础上创建了某碎屑岩气藏岩石物理模板,建立了弹性阻抗系数与孔隙度、含气饱和度间的关系,并应用于致密储层含气性解释中,取得较好效果。Ba等[29]基于Biot-Rayleigh波动方程实现了对非饱和岩石的多尺度理论建模,预测了不同尺度波响应特征与岩性、流体间的定量联系,给出了多尺度岩石物理图板,并利用该模板进行含气饱和度、孔隙度预测,预测结果与试气结果相吻合。
本文在前人研究的基础上,首先给出了改进型随机斑块饱和模型,并对该模型进行分析与验证;然后,基于改进型随机斑块饱和模型生成了多尺度岩石物理模板,利用多尺度地球物理数据进行标定;最后将多尺度模板应用于四川致密砂岩气层检测,分析其应用效果。
2 改进型随机斑块饱和孔隙介质模型
2.1 孔隙流体分布特征
图1为某砂岩样品水驱气过程中水随时间在岩石中分布的相对变化情况,蓝色为背景,浅色代表水,深色为气。干燥(图1a)和气饱和(图1e)时,岩石较为均匀。当含水饱和度超过40%(图1c)时,流体斑块开始聚集,非均匀性明显变强(图1d)。流体以不同形状、不同尺寸的斑块赋存于岩石中[11,28],分布具有随机性[4,20]。

图1 某砂岩样品中孔隙流体在不同时刻的分布情况(修改自参考文献[11])(a)干砂岩; (b)注水1小时后; (c)注水24小时后; (d)注水72小时后; (e)注气
2.2 MCRM模型分析与验证
改进型随机斑块饱和孔隙介质模型(The Mo-dified Continuous Random Model of Patchy Saturation, 简称MCRM), 是在宏观均匀介质背景上,加以孔隙流体非均质性导致的扰动构建的。有关模型细节可参考文献[26]。图2是MCRM模型示意图。
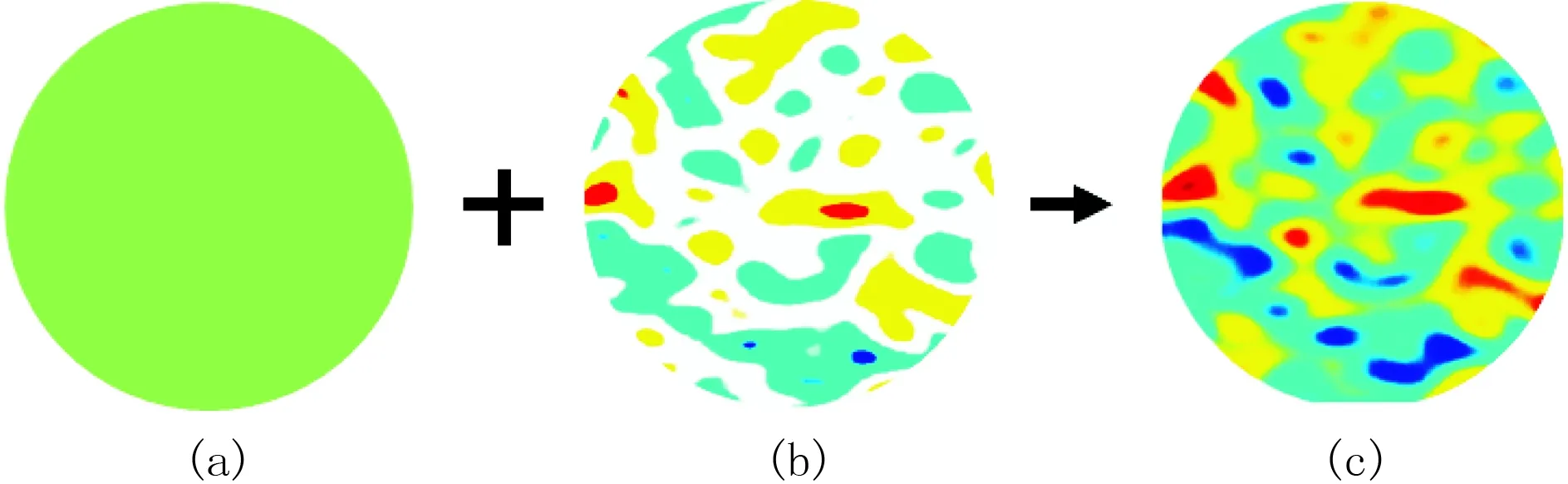
图2 随机斑块饱和孔隙介质模型示意图(a)背景介质; (b)流体扰动; (c)随机斑块饱和
根据MCRM模型,地震波的纵波模量计算公式为
exp(ikpsr)dr-Δ2]2
(1)
式中:Heff为地震波的纵波模量;H0为背景介质纵波模量;Δ1和Δ2是无量纲的数,满足
(2)
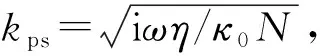
T1(kz)
(3)
(4)
(5)
式中:a、b和c分别为自相关长度因子;kzmax表示锥形函数的长度。
进而,地震波速度的计算公式如下
(6)
式中:veff表示地震波速度,ρ表示岩石密度。
地震波的衰减公式为
(7)
式(1)中,Δ2是频率无关项,是随机场H、C和G的加权求和,积分项与频率有关,代表流体的作用。当地震波通过部分饱和岩石时,由于饱气和饱水区域的可压缩性不同,两者间会形成孔隙压力梯度。为达到力学平衡,流体吸收能量发生流动,不同频率压力梯度平衡时间不同,进而导致频散和衰减现象的发生。
图3 MCRM模型数值模拟的是一块致密砂岩纵波速度随含水饱和度的变化。实验数据来自Murphy[30]利用共振棒技术测量的一块致密砂岩样品(φ=8.5%),其测量频率在5kHz左右。模型参数采用:岩石颗粒体积模量Kg=35GPa,密度ρg=2650kg·m-3;岩石骨架体积模量Kdry=7.14GPa,剪切模量Gdry=9.06GPa;水的体积模量Kf=2.25GPa,密度ρf=997kg·m-3;空气的体积模量Kair=0.0008GPa和密度ρair=100kg·m-3。水和空气黏滞系数根据文献[4]给定,ηwater=0.001Pa·s,ηair=0.00001Pa·s,渗透率根据孔隙度—渗透率经验关系给定。
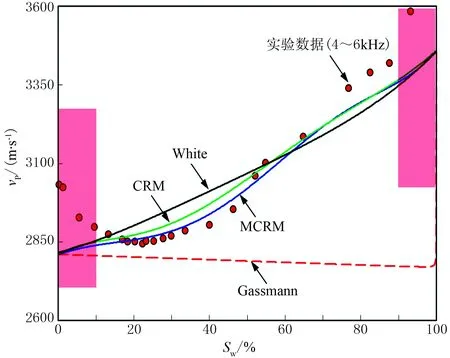
图3 MCRM模型估计的纵波速度随含水饱和度的变化与实验数据对比
在含水饱和度0~10%段,速度降低的可能原因是水吸附在岩石颗粒表面,形成水膜,岩石颗粒表面与流体间相互作用软化了岩石,降低了岩石速度。Endres等[31]在致密砂岩部分饱水的超声实验中也观测到这一现象。在高含水段(>90%),纵波速度急剧增长,此时水充填于大部分孔隙空间,对岩石骨架起到支持作用,从而加强了岩石的强度。为便于比较,同样利用White模型、随机斑块饱和模型(The Continuous Random Model of Patchy Saturation,简称CRM)和Gassmann模型模拟了该致密砂岩样品纵波速度随含水饱和度的变化,模型参数与MCRM相同。结果表明,White模型和CRM模型在饱和度0~10%和90%~100%间的模拟结果与实验数据吻合较差。在含水饱和度10%~90%段,MCRM模型较White、CRM和Gassmann模型具有优势,能较好地模拟纵波速度随含水饱和度的变化情况。
地下气藏通常没有完全气饱和的情况,因为孔隙介质中总有一部分水附着在岩石颗粒表面,为不可动水,而水饱和情况常见。气藏的形成是天然气驱替地层水的过程,且总是部分饱和的,一般气藏含气饱和度在微含气(
3 基于MCRM模型的致密储层多尺度模板
以四川盆地三叠系须家河组为例,建立多尺度岩石物理模板。须家河组致密砂岩孔隙度为1%~11%,图4是取心样品实测孔隙度分布,大部分样品孔隙度为5%~9%,总体上是低孔、低渗或特低孔、特低渗储层[1]。
选取一条地震测线开展储层定量预测工作,目标层为须家河组须二段。该段岩性多样,砂岩、泥岩纵向上相互叠置,岩性横向变化快、非均质性强。致密储层弹性特征与围岩差异不明显,地震多解性强[1]。数据包括过线两口井(Y2井、Y1井)岩石物理资料,目标层位均遇到含气层,其中Y2井为分析井,Y1井为验证井。

图4 实验测量样品孔隙度分布
首先,分析研究区地质报告得到该地区储层基本矿物构成,利用Voigt-Reuss-Hill平均公式计算固体颗粒弹性参数。干燥岩石骨架模量计算可根据Pride公式
(8)
(9)
式中:Ks和Gs分别是岩石颗粒体积模量和剪切模量;c和c′为经验固结常数,经验系数的求取需要与多尺度岩石物理数据进行标定和迭代,进而优化模型参数。
对于该致密砂岩储层,矿物成分除石英外还含有长石及黏土,长石体积模量大于石英,黏土的体积模量小于石英且变化剧烈。参考Murphy对致密砂岩取值,选取岩石颗粒体积模量Ks=35GPa,剪切模量Gs=44GPa, 密度ρs=2650kg·m-3; 水体积模量Kf=2.25GPa, 密度ρf=997kg·m-3; 空气体积模量Kair=0.0008GPa, 密度ρair=100kg·m-3。水和空气黏滞系数根据文献[4]给定,ηwater=0.001Pa·s,ηair=0.00001Pa·s。致密砂岩渗透率与孔隙度的关系很复杂,很难确定,其中孔隙结构是比较重要的影响因素之一。对于孔隙度及渗透率的关系,本文参考文献[29]给出,渗透率是孔隙度的指数函数,即κ=AeBφ,A和B均为经验参数。
图5是不同尺度下的AI-vP/vS交会图。为使模板更具普适性,本文收集了部分公开发表实验数据,用于多尺度模板的标定,数据来源为文献[32-34]。由图可见:
(1)超声频段AI-vP/vS交会图(图5a),数据来自21块样品,大部分实验数据与模板一致,不同孔隙度气饱和致密砂岩vP/vS为1.52~1.6。随着含水饱和度增加,vP/vS增加,且均在1.64以上。受岩石组分、孔隙结构等影响,纵波阻抗随含水饱和度需要说明的是,黄色圆点为气饱和砂岩,蓝色圆点为水饱和砂岩。本地区16块气饱和与水饱和砂岩超声测量数据来源于文献[33];收集的其他地区5块变饱和度致密砂岩超声测量数据中,孔隙度10.1%、7.1%、4.9%和3.8%的4块砂岩数据来自文献[32],孔隙度7.7%的1块砂岩数据为实验室测量。
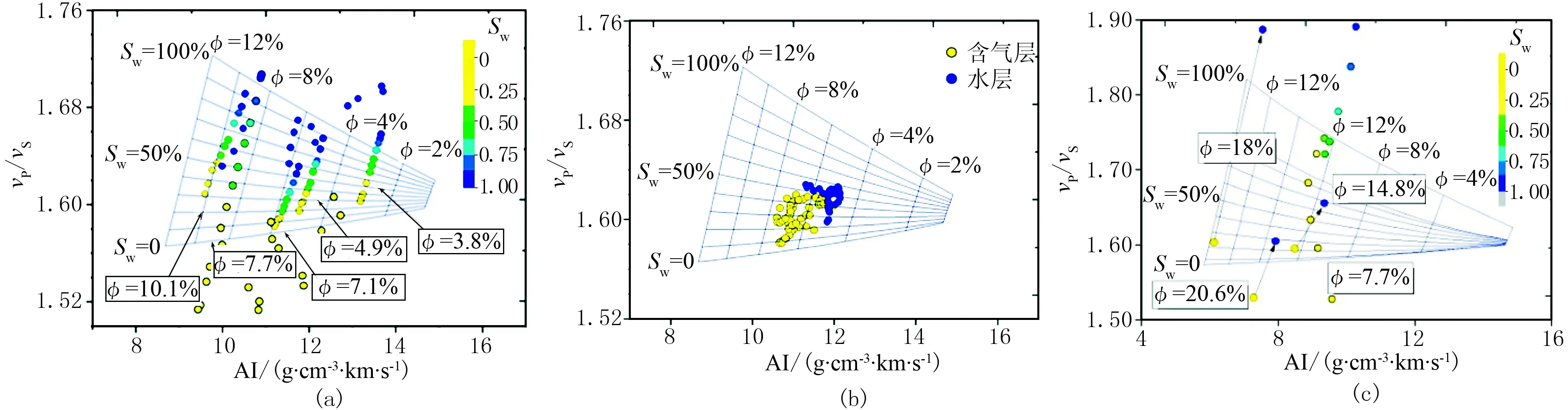
图5 不同尺度下的AI-vP/vS交会图(a)超声尺度; (b)测井尺度; (c)地震尺度
变化并非完全线性。超声频段岩石物理模板总体上可描述不同孔隙度、含水饱和度致密砂岩弹性性质的变化。
(2)在Y2井目标层段AI-vP/vS交会图(图5b)上,将测井解释含气层和水层投影在模板上。气层砂岩在模板的位置较为合理,然而,水层砂岩位置偏下,与气饱和砂岩在模板位置并未完全分开,其原因可能是测井解释水层砂岩微含气,其纵横波速度比与气层纵横波速度比相差不大导致[32,35]。
(3)由于地震频带岩石物理测量技术正处于发展阶段,各研究机构测量数据鲜有公开发表[36]。基于本文研究目的收集了3块砂岩气饱和与水饱和实验数据(来源于文献[34]),并且实验测量了孔隙度7.7%的变饱和度致密砂岩数据(图5c)。结果显示,模板较为清晰地反映地震频带岩石AI-vP/vS随孔隙度和含水饱和度的变化情况。
一些数据点超出了模板描述范围可能是因为岩石具有不同矿物组分和孔隙微观结构。其弹性参数随孔隙度和含水饱和度变化未必完全相同,但总体变化趋势一致。
4 致密砂岩气层检测
定量描述储层多尺度波响应特征的多尺度岩石物理图板可以灵活运用于不同尺度下弹性波反演及岩性识别。在常规地震勘探中,所使用地震尺度资料的主频一般可针对性使用地震尺度下的岩石物理图板,进而结合地震反演数据体,对目的层段的岩性与流体参数进行定量估算。
本例中,利用Hampson-Russell软件实现叠前地震反演,图6为Y2井的井—震标定结果,其中合成地震记录与实际地震记录相关系数为0.68(图6a),波形、幅值、相位等方面存在较大差别,特别是在黄色区域内,其原因可能是存在速度频散,工业界常见做法是做拉伸处理以提高井震匹配精度。本文在油田测井解释的基础上,通过MCRM模型对合成地震记录做速度校正处理。模型骨架参数及流体斑块特征参数参考文献[33]得到。尺度校正后合成地震记录与实际资料相关关系明显改善,相关系数变为0.76(图6b)。
图7为反演纵波阻抗(AI)与纵横波速度比剖面,揭示目标层段存在两套泥岩与砂岩储层,并形成夹层,“三明治”式的储盖组合特点符合这一地区地质沉积规律[33]。测井结果显示含气层与GR曲线指示结果一致。验证井的vP/vS与测井解释结果较为一致,说明反演结果是可靠的。
在得到该目标层段AI与vP/vS的基础上,利用地震尺度模板进行孔隙度和含气饱和度预测,最后利用验证井检验预测结果。图8为定量预测孔隙度与含气饱和度剖面,结果显示Y2井目标层段孔隙度范围约为5%~7%、含气饱和度为44%~56%,与测井解释结果较为接近。同时,预测了一有利气聚集区(黑色椭圆内),该区为构造高部位,且孔隙度、含气饱和度均较高,Y1井位于该区域内,后证实为高产气井。Y2井产气0.86×104m3/d,Y1井产气11.43×104m3/d。

图6 某工区井—震资料标定(a)原始测井数据合成地震记录(左)与实际地震记录(右)的对比; (b)MCRM模型校正后合成地震记录(左)与实际地震记录(右)的对比
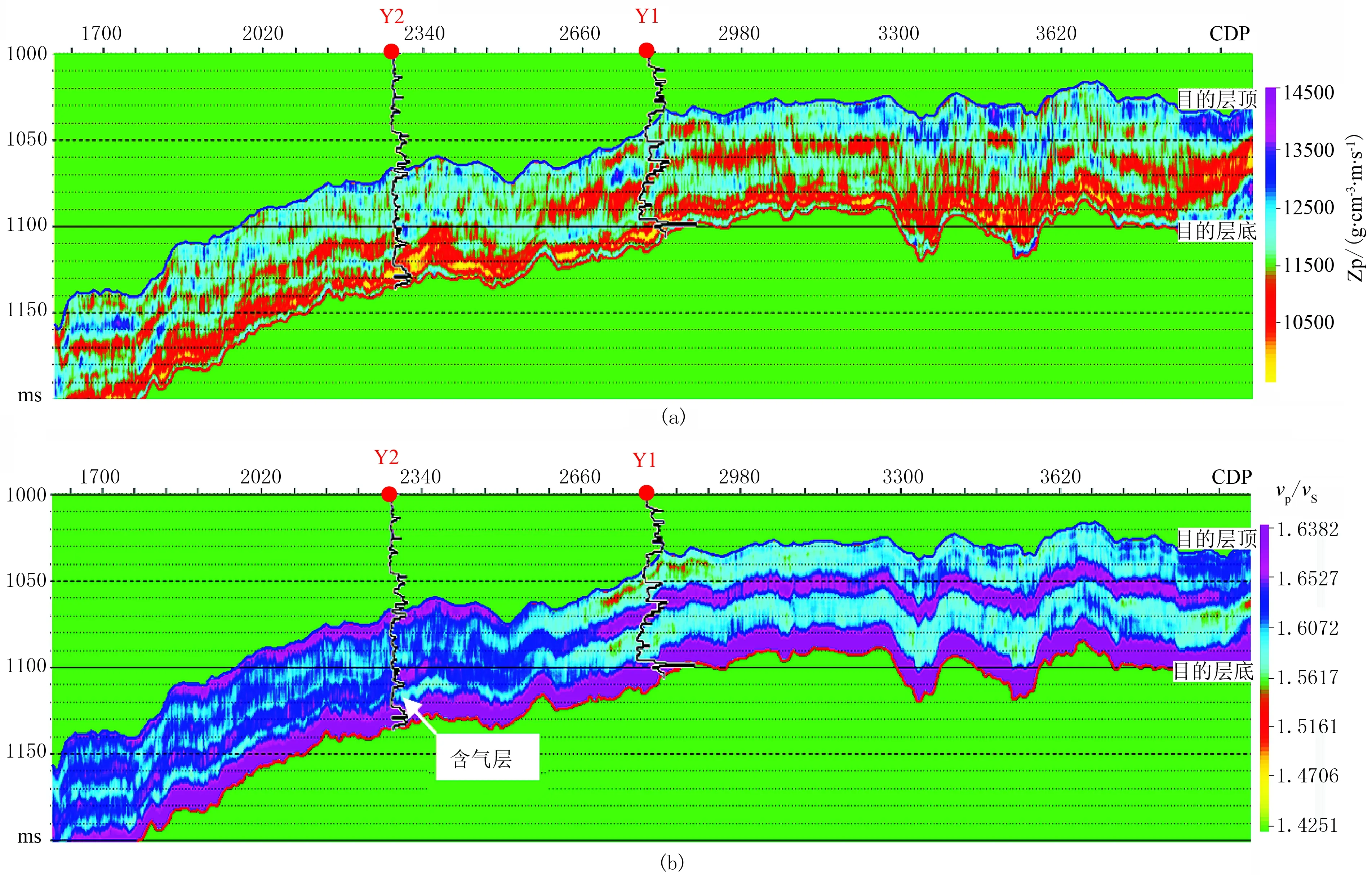
图7 AI(a)和vP/vS(b)剖面测井曲线为GR

图8 孔隙度(a)及含气饱和度(b)剖面测井曲线为GR
5 结论
本文首先介绍了改进型随机斑块饱和模型,并分析与验证了模型。其次,利用多尺度地球物理数据标定MCRM模型,优化模型参数,形成了多尺度岩石物理模板。最后,利用该模板对四川某地区致密砂岩气藏进行定量地震解释。预测孔隙度和含气饱和度剖面与测井结果吻合程度高,表明了该方法的适用性。
与无频散方法相比,考虑频散影响的岩石物理模型可以获得更多储层岩石信息,更客观地反映弹性参数与储层参数之间的关系,可有效降低定量解释多解性。但同时注意到MCRM模型仍假设固体基质宏观均匀,频散由介观尺度下流体引起,未考虑孔隙尺度喷射流及波长尺度宏观流机制。考虑非均匀介质孔隙结构、矿物成分的全频带(尺度)流体流动机制是进一步进行理论研究的方向。
感谢中国石油勘探开发研究院地震岩石物理实验室提供的帮助。
