中子活化水泥在线分析仪最小成本自动配矿算法研究
2018-03-15吴志强刘永超李岩峰
吴志强 刘永超 李岩峰
(丹东东方测控技术股份有限公司)
进入21世纪,随着工业领域对不可再生矿产资源的大量开发,高品位矿山资源逐渐减少,开采成本不断增加,降低生产成本和节能降耗已经成为企业发展的主题。在多种矿石原料可供选择的情况下,采用较低成本的原料和资源可以实现节能降耗。水泥企业为了降低生产成本和延长矿山寿命,希望利用中子活化水泥在线分析仪自动配矿系统,在保证质量指标的前提下,最大程度地采用低品位石灰石资源,实现最低成本的自动配料方案[1-3]。为此,从节省原材料成本和优化石灰石配矿角度出发,探讨了利用中子活化水泥在线分析仪实现最小成本自动配矿方案的可行性。
1 中子活化水泥在线分析仪自动配矿系统
中子活化水泥在线分析仪主要由测量装置、信号处理柜和主机组成。测量装置为模块化结构,不需切割皮带,可方便的绕皮带安装。运行时,皮带从测量装置内托槽上滑过,对流经的所有物料进行检测,整个检测过程不需取样,不接触物料,不影响皮带运行,即时给出成分结果[4]。如图1所示,载料皮带从测量装置中间滑槽穿过,信号处理柜安装于测量装置旁,主机安装于主控室。
中子活化水泥在线分析仪自动配矿系统主要由中子活化在线分析仪、GPS调度系统、控制网络组成(见图2)。中子活化在线分析仪安装于下山石灰石输送皮带上,实时检测下山石灰石各氧化物含量,分析仪主机根据实时检测值和中控室下达的质量控制指标,及时生成配矿方案,并由GPS调度系统执行自动配矿方案。
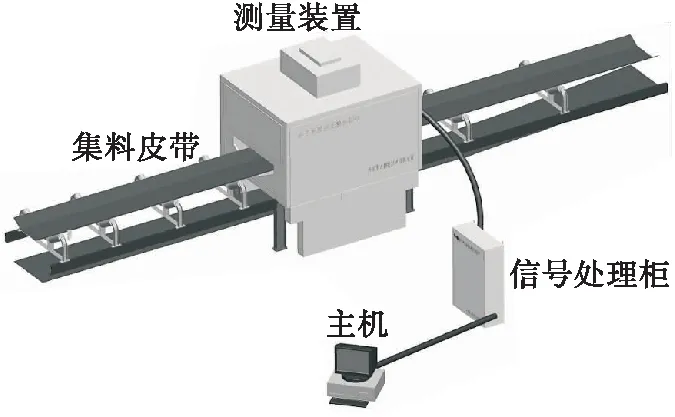
图1 皮带上在线分析仪安装示意
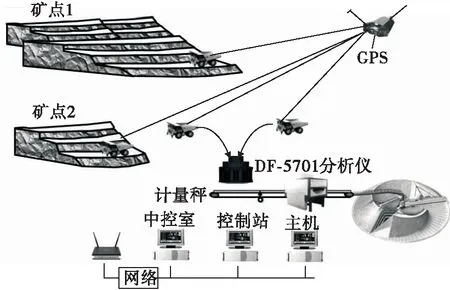
图2 中子活化水泥在线分析仪自动配矿系统示意
2 水泥自动配矿的控制指标要求
水泥生产工艺[5]的控制指标通常为三率值指标,考核方式为合格率。三率值分别为石灰饱和系数KH、硅酸率SM、铝氧率IM,三率值根据SiO2、Al2O3、Fe2O3、CaO 4种成分计算得到,计算公式如下:
(1)
(2)
(3)
合格率的计算方法为先给出合格指标,一组统计数据中合格数目所占的百分比为合格率。通常三率值的合格指标为:KH±0.02,SM±0.1,IM±0.1。
3 最小成本自动配矿算法研究
3.1 最优化算法
最优化是一门相当广泛的学科,它讨论决策问题的最佳选择之特性,构造寻求最佳解的计算方法。伴随计算机的高速发展和优化计算方法的进步,规模越来越大的优化问题得到解决[6]。线性规划是最优化算法的一种,可利用线性规划最优化算法结合在线分析仪实现石灰石最小成本自动配矿功能。
线性规划(Linear programming,简称LP)是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。它是运筹学的一个重要分支,广泛应用于军事作战、经济分析、经营管理和工程技术等方面。为合理利用有限的人力、物力、财力等资源作出最优的决策,提供科学的依据。
在自动化配矿过程中,为了满足配矿的各种约束条件,并实现最小成本的优化配矿,可利用MATLAB的线性规划工具求解最小成本的自动配矿算法。
Matlab规定线性规划的标准形式为:
(4)
式中,fT(x)是目标函数,不等式是线性归化问题的约束条件,记为s.t.。 线性归化求解目的是在约束条件限制下,求出目标函数值最小化的可行解。MATLAB中求解线性规划的命令为:
[x,fval ]=linprog(f,A,b)
[x,fval ]=linprog(f,A,b,Aeq,beq)
[ x,fval ]=linprog(f,A,b,Aeq,beq,lb,ub)
式中,返回的x为决策向量的取值;返回的fval是目标函数的最大值;f为价值向量;A和b对应的是线性不等式约束;Aeq和beq对应的是线性等式约束;lb和ub分别对应的是决策向量的下界向量和上界向量。
3.2 配矿模型建立
以5个矿点配矿为例,建立相应的配矿模型。
3.2.1 矿点成分
5个矿点的矿点成分见表1。
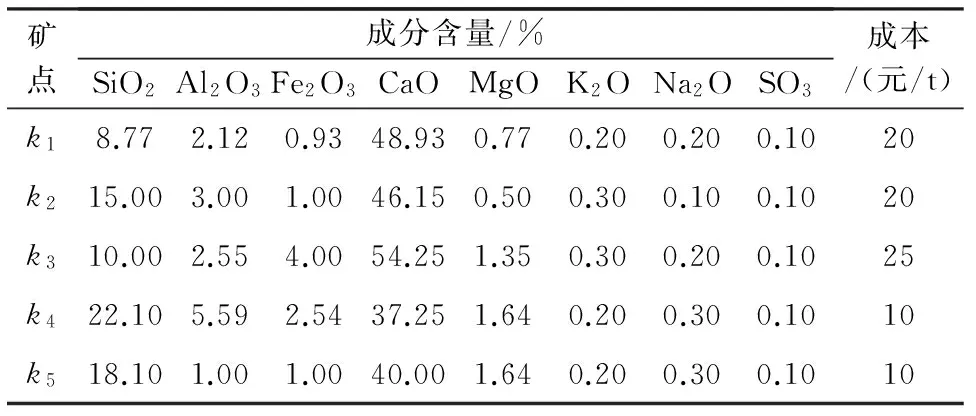
表1 矿点成分
3.2.2 矿点配比上下限约束
5个矿点的矿点配比上下限见表2。
表2 矿点配比上下限 %
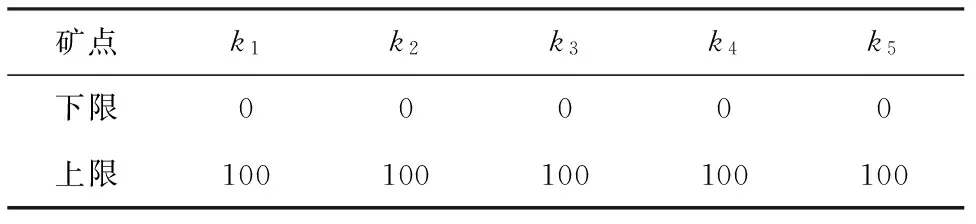
矿点k1k2k3k4k5下限00000上限100100100100100
3.2.3 控制指标与优先级
控制指标与优先级见表3。

表3 控制指标与优先级
3.2.4 配矿方程
以5矿点配矿为例,5矿点分别为(k1,k2,k3,k4,k5),控制目标数目M为4个,分别为(KH,SM,IM,CaO)。则建立如下矩阵与方程,如公式(5)和(6)。
其中,式(5)为配矿响应矩阵,通过求解公式(6)的线性方程组即可求得各矿点(k1,k2,k3,k4,k5)的配矿比例(x1,x2,x3,x4,x5)。
以5矿点配矿为例,可以扩展到2矿点,3矿点,4矿点,6矿点,直到N个矿点的配矿方程。
(5)
(6)
依据矿点个数N和控制指标个数M,将配方方案的求解分3种情况:
(1)第1种情况,控制指标的个数M≥(矿点个数N)时,配矿方程组无解。
(2)第2种情况,控制指标的个数M=(矿点个数N-1)时,配矿方程组有且仅有一组解,即有1种配矿方案。
(3)第3种情况,控制指标的个数M<(矿点个数N-1)时,配矿方程组有多组解,即有多种配矿方案。
针对第3种情况,当矿点个数较多,出现多种配矿方案时,从成本最小化角度出发,考虑到各矿点的成本,利用线性规划算法,求出成本最小化的配矿方案。
建立目标函数如下:
(7)
式中,Cn为矿点kn的单位成本,元/t;Xn为矿点kn的配矿比例。
由于各矿点生产条件的限制,还有配矿比例上下限约束,如下:
lb≤Xn≤ub,
(8)
式中,lb为矿点kn配矿比例下限,ub为矿点kn配矿比例上限。
由公式(6)、(7)、(8),通过线性归化算法,可以求得成本最小的配矿方案。
理论上,N个矿点最多可以有(N-1)个控制指标,控制指标个数过多可能出现无解情况。当方程组无解时,可依次减少控制指标个数,直至求得合理化的配矿方案。例如,5个矿点,控制指标有4个(KH,SM,IM,Ca),当方程组无解时,将控制指标减少为3个(KH,SM,IM),如果有解,则输出配矿方案;如果仍然无解,则将控制指标减少为2个(KH,SM),依次类推,直至求出配矿方案。
3.3 配矿软件编写
配矿软件主要分为两部分,一部分为功能与界面模块设计,另一部分为配矿配方生成模块设计。前一部分的开发软件采用vc6,后一部分主要的开发软件为matlab7,生成库函数,供vc6调用。两部分完成后,进行数据接口调试与模拟测试。
利用Matlab的线性规划函数linprog(),部分代码如下:
f=Cost(1∶5);
A=[1 1 1 1 1;K1K2K3K4K5;L1L2L3L4L5;M1M2M3M4M5;N1N2N3N4N5];
b=[1;Py(9,14);Py(10,14);Py(11,14);Py(12,14)];
lb = [Pf(1,1);Pf(2,1);Pf(3,1);Pf(4,1);Pf(5,1)]/100;
ub = [Pf(1,2);Pf(2,2);Pf(3,2);Pf(4,2);Pf(5,2)]/100;
[x,fval,exitflag,output,lambda] = linprog(f,[],[],A,b,lb,ub);
k1_fp=x(1)*100;
k2_fp=x(2)*100;
k3_fp=x(3)*100;
k4_fp=x(4)*100;
k5_fp=x(5)*100;
3.3.2 Matlab求解结果
以5矿点配矿为例,控制指标为4个,分别为KH=1.2,SM=4.0,IM=1.8,CaO=49时,利用标准的求解线性方程组算法,求得配矿方案见表4。
表4 各矿点标准配矿方案 %

矿点k1k2k3k4k5百分比48.718.34.90.927.2
当控制指标为3个,分别为KH=1.2,SM=4.0,IM=1.8时,利用线性规划算法,求得成本最小的配矿方案见表5。
表5 各矿点最小成本配矿方案 %

矿点k1k2k3k4k5百分比61.302.06.230.5
经计算,第1种方案的配矿成本为17.4元/t,而第2种最小成本的配矿成本为16.4元/t,每吨节约成本1元,节约成本达到6%,且满足了水泥企业的主要控制指标三率值(KH,SM,IM)要求,达到了降低生产成本的目标。一条5 000 t/d的水泥生产线,每天需要石灰石原料约6 000 t,每天节约原料成本约6 000元,按每年生产天数300 d计算,每年仅原材料就能节省成本约180万元。
4 结 论
(1)中子活化水泥在线分析仪自动配矿系统适用于多个石灰石矿点配矿情况。
(2)利用线性规划算法可以实现最小成本的多矿点自动配矿。
(3)水泥企业使用中子活化水泥在线分析仪自动配矿系统后,可减小预均化堆场规模,甚至可以取消预均化堆场;合理使用原料,降低成本;减少石灰石原料成分波动,提高低品位石灰石利用率;延长矿山使用寿命,提高产品合格率。
[1] 刘永超,张 伟,龚亚林,等.中子活化元素在线分析仪在氧化铝生产中的节能分析[J].世界有色金属,2014(6):49-51.
[2] 宋青锋,张 伟,龚亚林,等.利用瞬发γ中子活化分析技术对铜镍矿石进行在线检测的应用研究[J].世界有色金属,2014(2):72-73.
[3] 宋青锋,龚亚林,张 伟,等.利用PGNAA系统对铝土矿石进行在线检测的可行性研究[J].中国矿业,2015(10):172-173.
[4] 陶俊涛,卢元利,李剑锋,等.中子活化元素在线分析仪的结构与应用[J].煤质技术,2016(1):11-13.
[5] Rockwell Automation Technologies,Inc.Bulk Material Blending Control:US 20100082157A1[P].2010-04-01.
[6] 袁亚湘,孙文瑜.最优化理论与算法[M].北京:科学出版社,1997.
