基于QPSO-ELM的某型涡轴发动机起动过程模型辨识
2018-11-30伍恒李本威张赟杨欣毅
伍恒,李本威,张赟,杨欣毅
海军航空大学 航空基础学院,烟台 264001
航空发动机是一个高度非线性的时变系统,建立准确的航空发动机模型可用于发动机的健康监测与状态评估、性能分析与故障诊断以及控制规律设计等多方面研究。目前建立航空发动机模型的方法主要有两种:一种是分析部件气动热力特性的解析法,另一种是把发动机作为一个整体,对输入输出发动机的参数之间的函数关系进行分析的数据辨识法。解析法需要充足的发动机部件特性,但发动机起动阶段的转子部件特性往往不可获得,而且建模过程比较复杂,需要进行大量的假设、近似处理和反复的迭代运算。近年来,基于数据驱动的模型辨识方法得到越来越多的研究。传统的辨识方法主要有最小二乘法以及子空间状态辨识法等,但它们都是假定发动机是线性时不变系统,因此精度较低。而且发动机起动过程是非线性大偏差的,不存在稳态工作点,目前还无法确定模型或传递函数的结构。以人工神经网络(Artificial Neural Networks, ANN)、支持向量机(Support Vector Machine, SVM)和极限学习机(Extreme Learning Machine, ELM)为代表的数据挖掘机器学习算法展现出了良好的非线性逼近能力。
针对建立航空发动机起动过程辨识模型,Asgari等[1]利用外部输入非线性自回归(Nonlinear Auto Regressive models with eXogenous inputs, NARX)神经网络建立了某型单轴燃气涡轮起动阶段模型,并对模型进行了仿真分析;Pogorelov等[2]利用动态神经网络对一个双轴燃气轮机差分形式的非线性动态模型进行辨识,并应用于起动控制模式;陈超和王剑影[3]使用ANN对发动机起动过程进行辨识与仿真分析,但以上采用的ANN方法常常存在局部极小值、过学习等问题;李应红[4]和王冠超[5]等分别提出使用SVM以及优化改进的SVM来辨识发动机起动过程,取得了不错的效果。ELM[6-8]是单隐含层神经网络,仅需设置输入权重和隐含层结点数,就能产生唯一的最优解,使得其学习效率大幅提升,而且相关研究表明其非线性拟合能力要优于一些传统的ANN和SVM算法[9-11],但仍需进行参数的优化选取。
量子粒子群优化(Quantum-behaved Particle Swarm Optimization, QPSO)算法中粒子搜寻的位置由概率密度函数确定,取消速度参数,不仅简单,而且算法稳定性好,具有较强的全局搜索和寻优能力[12-14]。文献[15-17]在典型的回归和分类问题上进行试验,证明了基于QPSO选取ELM特征参数算法的有效性。
鉴于上述分析,本文提出一种基于QPSO-ELM的某型涡轴发动机起动模型数据驱动辨识方法。首先构建基于状态空间法描述的某型涡轴发动机起动过程分段模型,然后结合发动机起动试验数据,采用QPSO-ELM算法对该起动模型进行辨识和验证,最后对比不同方法的回归辨识效果,表明本文提出的一种基于QPSO-ELM的某型涡轴发动机起动过程模型辨识方法的可行性和优越性,为进行不同大气条件下的发动机起动性能递推估算以及进一步研究该型发动机起动控制规律优化并对发动机进行监控和健康状态的评估奠定基础。
1 基于QPSO的ELM算法原理
1.1 ELM概述
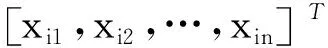
Hα=T
(1)

(2)
式中:H+为隐含层输出矩阵H的Moore-Penrose广义逆矩阵。
1.2 QPSO算法
粒子群优化(Particle Swarm Optimization, PSO)算法是基于群体进化的算法,认为群体中个体之间的信息共享能提供进化的优势,群体间个体的合作与竞争能实现优化问题的求解[18-20]。Sun等[21]提出的QPSO算法是在PSO算法的基础上引入量子力学原理,在量子空间中,通过波函数来描述粒子的状态,求解薛定谔方程得到粒子在某一点出现的概率密度函数。粒子移动的搜索方程可表示为
(3)
(4)
(5)
(6)

1.3 基于QPSO的ELM特征参数优化流程
利用QPSO算法优选ELM的特征参数不仅包括输入权重和隐含层偏置,也包括隐含层神经网络的结构或者说隐含层神经元的个数。具体的优化流程如下:
步骤1初始化。首先随机生成粒子种群,种群数量一般取30~50即可。种群当中的每一个粒子Li由一组输入权重、隐含层偏置和s变量组成,即
(7)

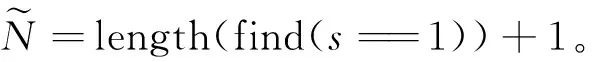
(8)

步骤2适应度函数值的计算。粒子的适应度函数值计算采用预测输出与目标输出的均方根误差来实现,QPSO寻优的目标即为最小化适应度函数。
(9)
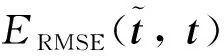
步骤3更新粒子的个体历史最好位置pbesti和种群历史最好位置gbest,重新根据式(4)和式(5)计算每一个粒子的局部吸引点和平均最好位置,再根据式(3)更新每一个粒子新的位置。
步骤4重复步骤1~步骤3直到达到最大迭代次数。这样即可针对实际问题,得到ELM优选的特征参数,再利用优选特征参数的ELM进行分类或回归辨识的应用。
文献[15-17]详细描述了利用几个经典函数和数据集验证QPSO-ELM方法的分类和回归辨识效果,以及该方法与其他算法性能的对比分析,不再赘述。结果表明QPSO-ELM方法的回归辨识效果更好。
2 某型涡轴发动机起动过程模型辨识方法
2.1 某型涡轴发动机起动过程模型建立
航空发动机模型具有时变非线性特点,某型涡轴发动机是由燃气发生器和与减速器相连的自由涡轮组成,通过减速器的输出轴使发动机功率输出。对于一个动力学系统或过程,通常有两种类型的数学描述,即输入输出描述和状态空间描述。状态空间描述可以作为系统或过程的一种完全描述,建立发动机起动状态空间模型,需找到能完全表征起动过程时间域行为的最小内部状态变量组。在某型涡轴发动机的起动过程中,起动机、发动机、点火系统、供油系统以及负载系统等相互配合工作,协同完成不同大气条件下的发动机起动。发动机起动过程模型结构如图1所示。
其中,数学模型的核心是发动机的气动热力特性,模型的输入量为大气条件、起动机特性、燃烧室供油特性(在正常起动的情况下,点火特性可以与供油特性一起考虑)以及负载特性;模型的输出量为发动机起动过程状态和性能。因此,用状态空间法描述的起动模型的一般形式为
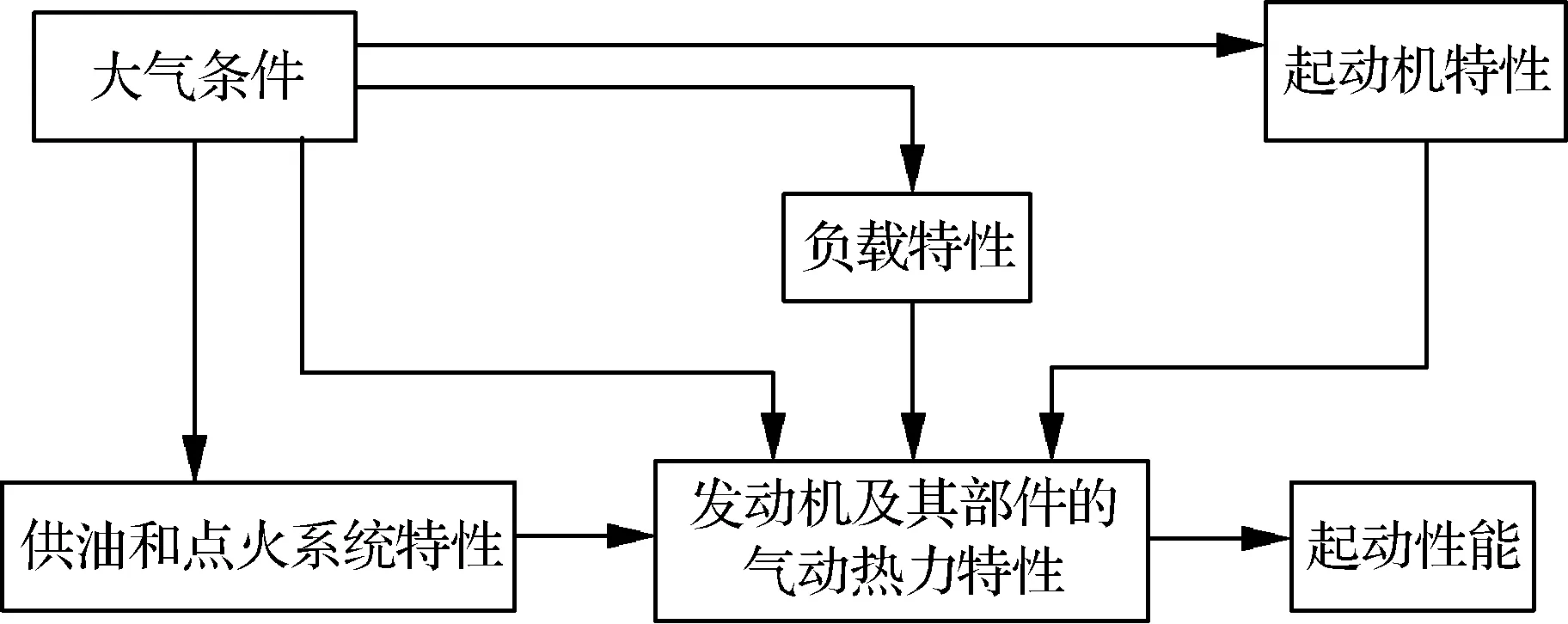
图1 发动机起动过程模型结构Fig.1 Structure of model for engine starting process

(10)
式中:T0、p0分别为大气温度和压力;Ns为起动机的输出功率;Nl为负载阻力矩;Wf为燃烧室燃油消耗量;k为样本集中采样数据点对应的时刻;x为状态向量;y为输出向量。由于发动机起动过程的负载阻力在常温环境变化不大的条件下较小,可以不予考虑。当考虑发动机转子惯性和燃烧室的能量存储以及热损失时,分别取燃气发生器转子转速ng、发动机输出轴转速nr和燃气涡轮后温度T4作为状态变量。对于状态空间模型,取输出向量与状态向量元素相同,即可得到离散形式的发动机起动非线性动态数学模型。
某型涡轴发动机的起动过程主要可以分为3个阶段,如图2所示(注:实际转速上升为非线性),图中t为时间。不同阶段模型的输入输出量不一样,因此,为了提高准确度,本文建立起动过程分段非线性模型。
第1阶段是起动开始后1.25 s内,由起动机发出功率单独带动燃气涡轮工作阶段。发动机转速在设定的时间内达到(0.08~0.12)·33 400 r/min,并成功触发起动点火燃油系统开始工作点火。由于第1个阶段只有起动机带转并无供油点火,燃气涡轮后温度接近大气温度,可得发动机非线性起动模型为
ng(k+1)=f1(ng(k),T0,p0,Ns(k))
(11)
第2阶段是供油点火燃烧,由起动机和燃气发生器共同发出功率带动发动机加速工作阶段。起动燃油调节装置按燃油调节规律供油,持续稳定燃烧,起动机和燃气发生器共同带动发动机在设定的时间内加速到脱开起动机的转速14 000 r/min。发动机非线性起动模型为

图2 发动机起动过程不同阶段示意图Fig.2 Diagram of different stages of engine starting process
(ng(k+1),nr(k+1),T4(k+1))=f2(ng(k),nr(k),T4(k),T0,p0,Ns(k),Wf(k))
(12)
第3阶段是当燃气发生器转速达到14 000 r/min的自立转速时,起动机断开,由燃气发生器单独产生功率带动发动机加速工作到地面慢车状态,即完成起动,整个起动过程不能超过60 s。发动机非线性起动模型为
(ng(k+1),nr(k+1),T4(k+1))=f3(ng(k),
nr(k),T4(k),T0,p0,Wf(k))
(13)
2.2 基于QPSO-ELM的起动模型辨识方法
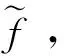
ELM在进行函数逼近时,首先利用QPSO算法对其输入权重、隐含层偏置和隐含层神经元个数等特征参数进行寻优,寻优的目标即为最小化适应度函数,也即最小化预测输出与目标输出的均方根误差值。如图3所示为ELM的网络结构图。
(14)
其矩阵表示形式如式(1)所示,H、α、T的具体表达式为
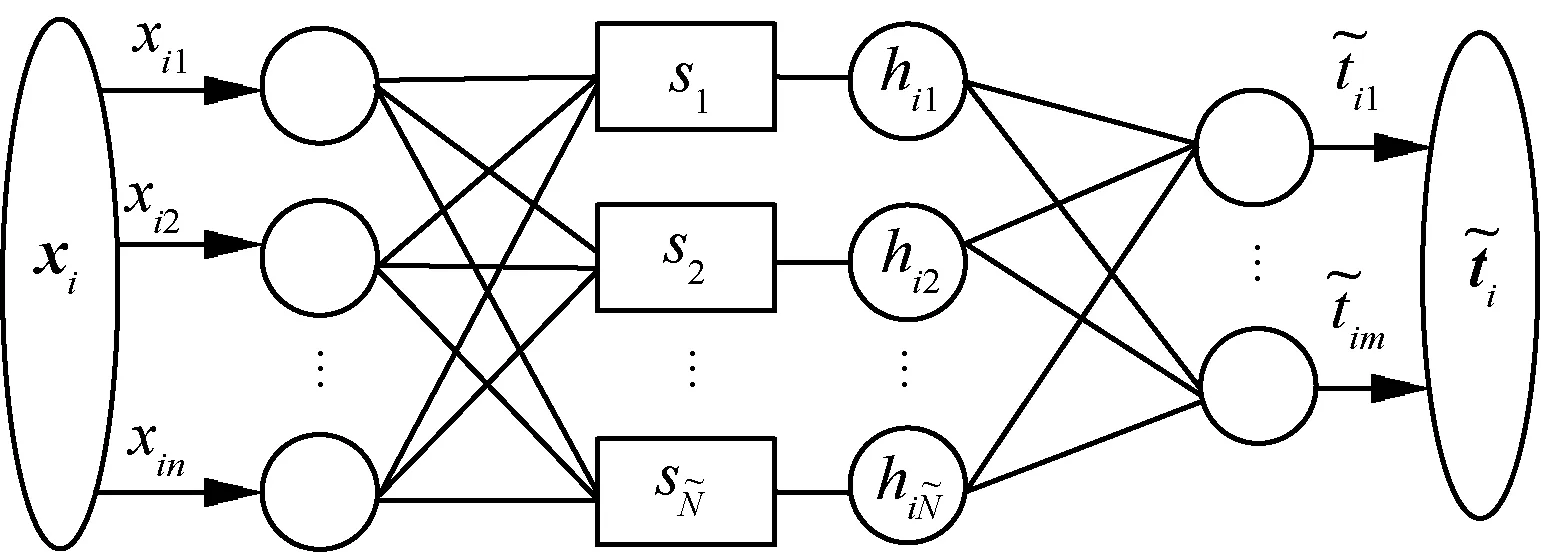
图3 ELM的网络结构Fig.3 Network structure of ELM
最后,ELM的输出为

(15)
综上,基于QPSO-ELM的某型涡轴发动机起动模型辨识的具体流程如图4所示。
步骤1根据某型涡轴发动机起动过程原理,建立包含输入输出量函数关系的分段非线性起动模型。
步骤2选取发动机起动试验数据,建立模型辨识的训练和验证样本集,并进行样本集的平滑、滤波和归一化处理。

图4 起动模型辨识的具体流程Fig.4 Specific process of starting model identification
步骤3设置QPSO算法的种群粒子数量和最大迭代次数等基本参数,利用QPSO算法对ELM的特征参数寻优。
步骤4结合模型辨识的训练样本集,利用优选特征参数的ELM对建立的某型涡轴发动机分段非线性起动模型进行回归辨识。
步骤5利用验证样本集对建立的发动机起动过程辨识模型进行验证。
步骤1~步骤5构成了基于QPSO-ELM的某型涡轴发动机起动模型的辨识方法。
3 辨识结果分析
3.1 模型辨识样本数据的选取与处理
为研究某型涡轴发动机的起动特性,工厂在2016年针对该型涡轴发动机进行了1 000 h试车试验。选取4组录取的被试发动机起动过程试验数据作为训练和验证样本集,这4组数据分别在9.2、18.3、26.8、34.6 ℃下测得。根据该型涡轴发动机起动试验采集的数据种类,结合建立的发动机分段非线性起动模型,确定样本参数为:大气温度T0、大气压力p0、燃烧室燃油消耗量Wf、起动机发出的功率Ns(由测量的起动机电压和电流,结合起动机效率计算得到)、燃气发生器转子转速ng、发动机输出轴转速nr以及燃气涡轮后温度T4。
将每组发动机起动试验数据按照起动过程的3个阶段分为3段数据集,每个阶段模型的具体输入输出量根据模型结构方程式(11)~式(13)对应选取。第1阶段每50 ms选取一个数据,4组数据总共100个数据点作为起动过程第1阶段的样本集。第2、3阶段分别均匀选取50个数据点,每个阶段4组数据各200个数据点分别作为第2、3阶段样本集。其中一组数据选取的起动过程3个阶段的部分样本数据如表1所示。
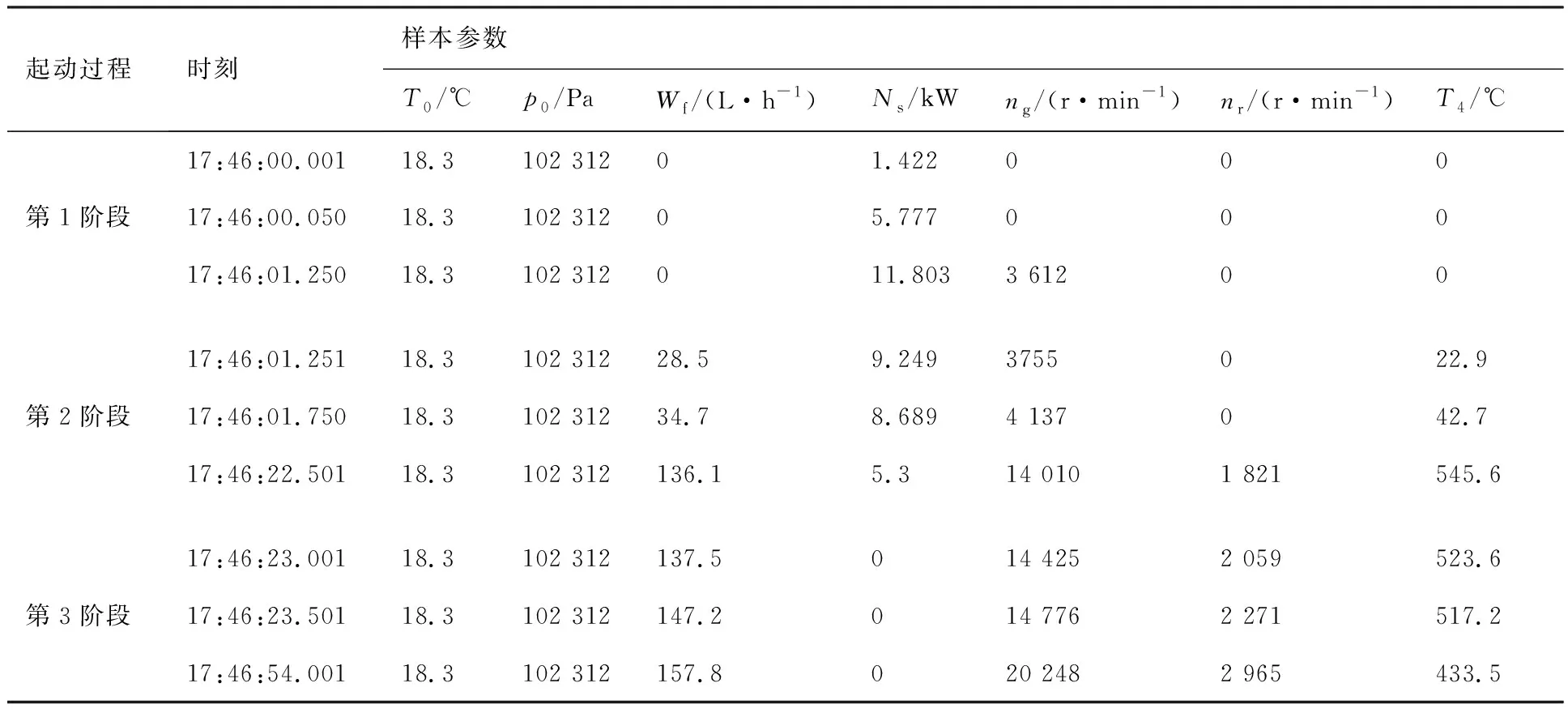
表1 一组发动机起动过程3个阶段部分样本数据Table 1 Partial data in three stages of starting process of a certain engine
对样本数据进行异常数据剔除、平滑与滤波处理,具体计算公式参照文献[22]。由于不同的变量取值范围差异较大,需要以归一化处理后的数据作为训练与验证样本,并在完成训练和验证后对变量进行还原。
为了减少人为数据分组带来的误差,本文采用随机数据分组的方式进行处理,随机选取其中3组数据作为训练样本进行训练,并用另外1组数据作为验证样本,分别对比不同训练与验证样本情况下得到的起动过程辨识模型的辨识精度。
3.2 模型辨识结果
选取样本数据并处理完之后,设置好QPSO算法的基本参数,主要包括:种群粒子数量为30,最大迭代次数为30,即可利用QPSO算法对ELM的特征参数寻优,并结合模型辨识的训练样本集,利用优选特征参数的ELM对建立的某型涡轴发动机分段非线性起动模型进行回归辨识。将验证样本输入到辨识模型中计算对应的输出,并对比模型辨识结果和实测数据来验证建立的发动机起动过程各阶段辨识模型。由于各离散数据点的函数值均为输出参数的一步预测值,通过验证计算可得,各输出参数数据点的预测值与实测值相对偏差较小。此外,各输出参数数据在发动机起动过程中的实际变化是连续的,从而完成起动过程不同阶段连接段辨识数据点的连接。最后将起动过程3个阶段的辨识结果合并即可得到某型涡轴发动机起动过程辨识模型。
其中,以一组环境温度为18.3 ℃条件下测得的数据作为验证样本时,输出参数ng、nr和T4的辨识结果与实测数据的对比如图5所示。
从图5可看出,输出参数ng、nr和T4的辨识结果都良好地逼近了实测数据,验证样本中各输出参数不同数据点的最大相对误差分别为:1.34%、1.63%和2.2%,说明本文提出的基于QPSO-ELM的起动模型辨识方法是可行的。
轮流以选取的4组发动机起动试验数据中的3组数据作为训练样本,另外1组数据作为验证样本,对某型涡轴发动机起动模型进行优化辨识,并用验证样本对辨识得到的模型进行验证,可得不同验证样本各输出参数辨识结果与实测数据的最大相对误差统计分析的盒状图如图6所示。
从图6可看出,不同验证样本验证得到的输出参数ng、nr和T4的辨识结果和实测数据的最大相对误差均未超过3%,最大相对误差均值分别为:1.358%、1.628%和2.195%,表明本文采用的QPSO-ELM辨识得到的某型涡轴发动机起动模型的精度满足实际应用的精度需求。


图5 输出参数的辨识结果与实测数据对比Fig.5 Comparison of output parameters between identification results and test datas
3.3 不同方法辨识效果的对比

图6 不同验证样本各输出参数辨识精度盒状图Fig.6 Box chart of identification accuracy of output parameters in different verification sample datasets
为了更好地说明基于QPSO-ELM辨识某型涡轴发动机起动模型的优越性,利用相同的模型训练与验证样本集,分别对比QPSO-ELM、ELM、SVM以及反向传播(Back Propagation, BP)神经网络4种方法的辨识效果。其中,ELM的隐含层神经元个数设置为回归辨识效果相对最好的值80,输入权重和偏置值由算法随机给定。SVM在进行回归辨识时的参数取值通过合理调整设置为:平衡因子C=100、不敏感度ε=0.008以及径向基核函数参数σ=4.5;BP神经网络采用广泛应用的Levenberg-Marquardt优化算法结构,并选用3层BP网络,其中隐含层结点数选为辨识效果相对最好的值7,MATLAB R2010b中有集成的工具包。表2为不同的辨识方法对某型涡轴发动机起动模型进行辨识,验证得到的输出参数ng、nr和T4的辨识结果与实测数据的最大相对误差以及最大相对误差均值的对比。图7更为直观地对比了不同方法的不同输出参数最大相对误差的均值。表3为4种不同方法的平均训练时间对比。
从表3可看出,ELM的收敛速度明显快于SVM和BP神经网络,这是由于ELM是单隐含层神经网络,网络结构简单,且相比于SVM,只需设计一个ELM即可实现多输入多输出模型的辨识,算法复杂度低,而相比于BP神经网络无需进行反复的正向计算和逆向的误差修正,使得学习效率大幅提升。从表2和图7可看出,ELM的辨识精度高于SVM,而ELM和SVM的辨识精度要显著高于BP神经网络,有效地避免了BP神经网络在训练时容易陷入局部极值的问题。本文采用的QPSO-ELM方法的平均训练时间相对较高,是因为需要对所有粒子进行适应度函数值评估和迭代寻优,其辨识精度要高于其他3种方法。
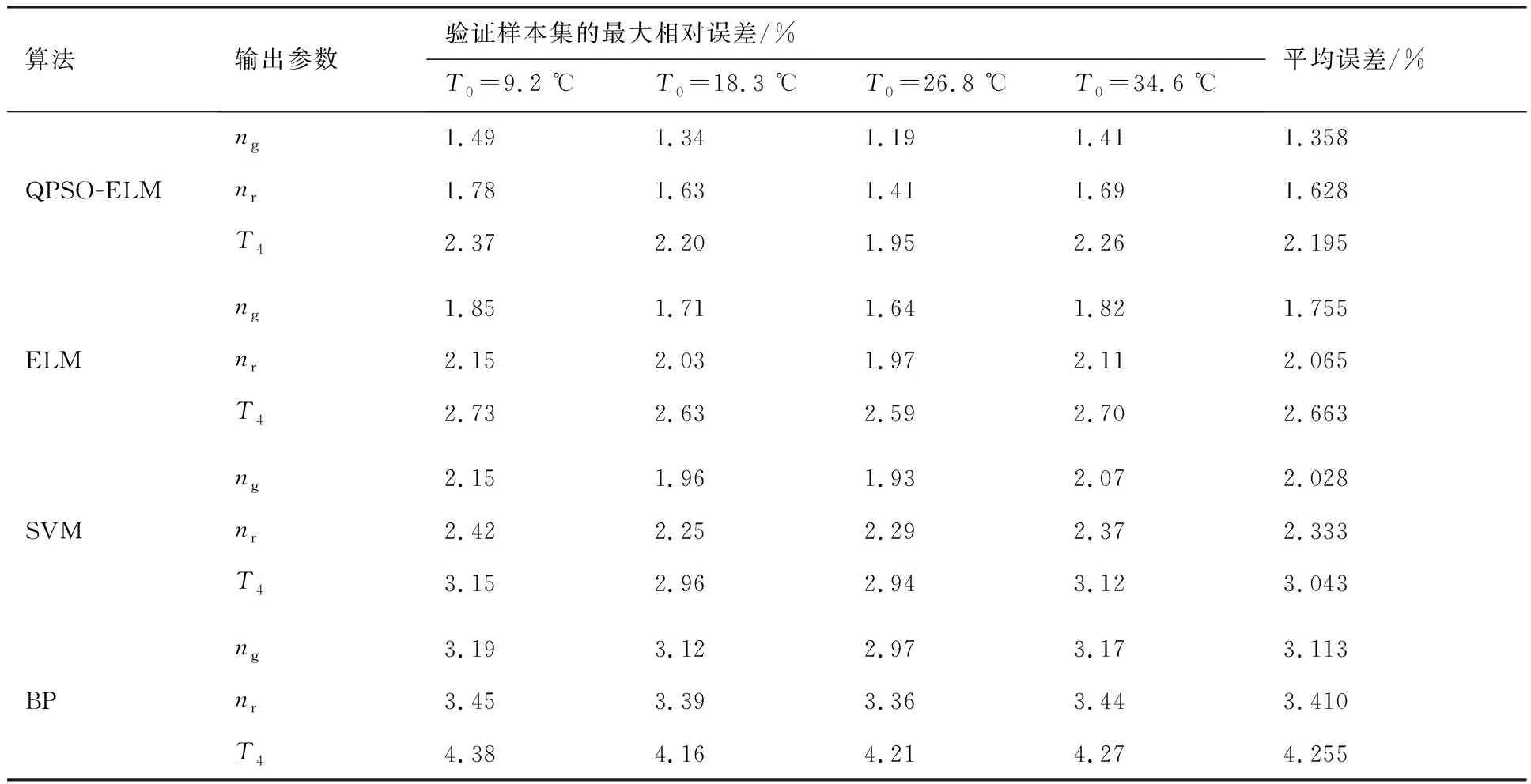
表2 不同方法辨识精度的对比Table 2 Comparison of identification accuracy of different methods
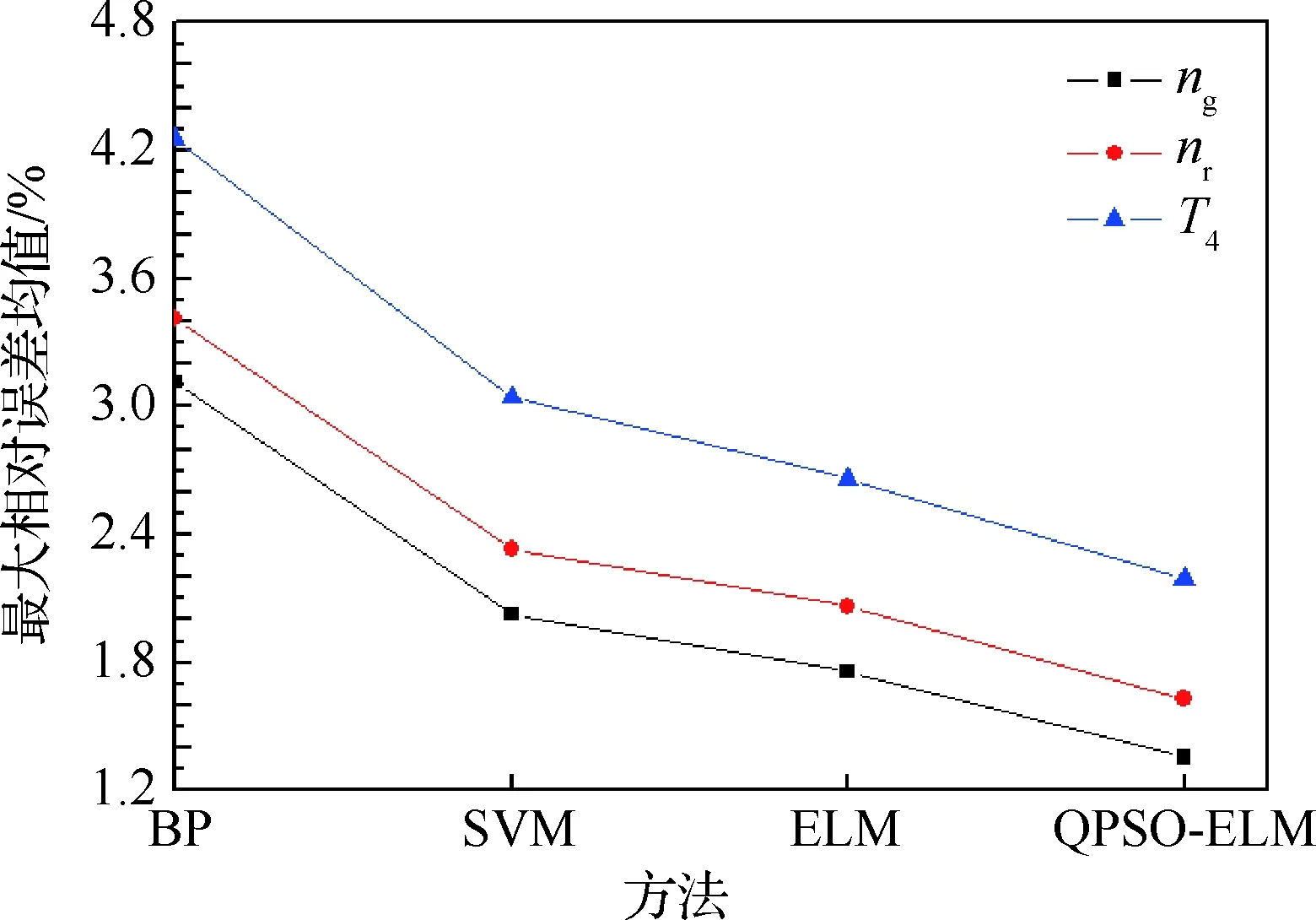
图7 不同方法3个输出参数的平均最大相对辨识误差Fig.7 Mean maximum relative identification error of three output parameters by different methods
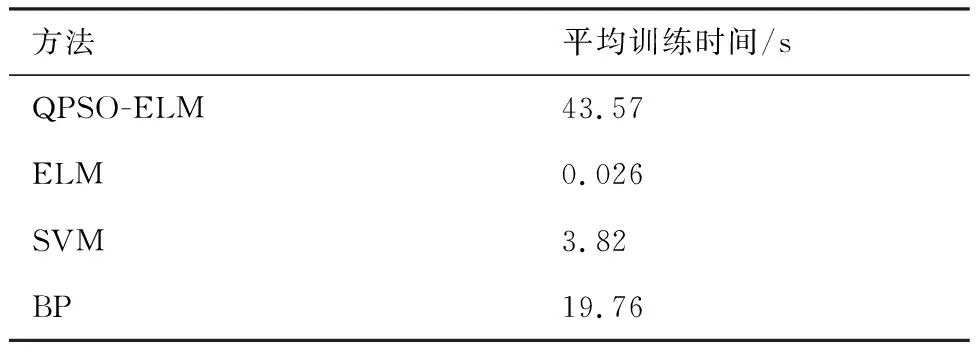
表3 平均训练时间对比Table 3 Comparison of mean training time
4 模型应用范围
基于QPSO-ELM辨识得到的某型涡轴发动机起动过程辨识模型可用于对其他大气条件下的发动机起动性能进行递推估算,模型递推估算结构如图8所示。
若已知某些大气条件下的燃烧室供油特性和起动机特性,再给定起动过程不同阶段输出参数的初始值,即可根据起动过程不同阶段辨识模型逐次递推估算出这些大气条件下发动机的起动性能,从而为发动机的起动状态进行监控。当发动机对起动供油调整螺钉适当调节时,仍可利用递推估算的方法对调整供油特性后的发动机起动性能进行估算,从而为起动性能调整试验提供指导。此外,利用起动过程不同阶段辨识模型还可进一步研究发动机起动控制规律的优化问题。
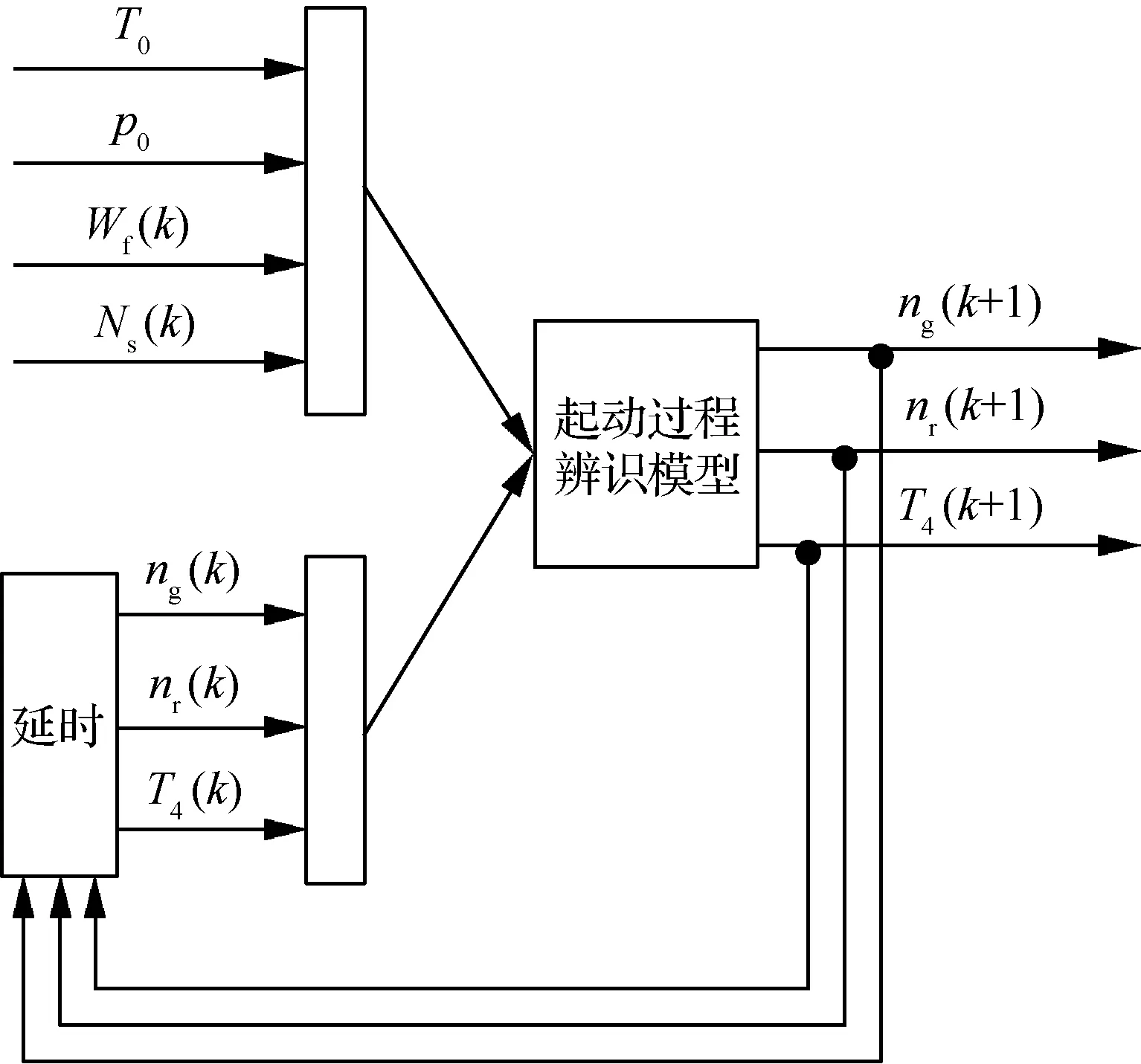
图8 起动性能的模型递推估算Fig.8 Model recursive estimation of starting characteristics
5 结 论
本文提出了一种基于QPSO-ELM的某型涡轴发动机起动模型数据驱动辨识方法,通过构建基于状态空间法描述的某型涡轴发动机起动过程分段模型,结合发动机起动试验数据,采用QPSO-ELM算法对该起动模型进行辨识,可得如下结论:
1) 输出参数燃气发生器转子转速ng、发动机输出轴转速nr和燃气涡轮后温度T4的辨识结果都良好地逼近了实测数据,证明本文提出的基于QPSO-ELM的起动模型数据驱动辨识方法可行。
2) 采用不同验证样本验证得到的输出参数ng、nr和T4的辨识结果和实测数据的最大相对误差均值分别为:1.358%、1.628%和2.195%,表明本文采用的QPSO-ELM辨识得到的某型涡轴发动机起动模型的精度满足实际应用的精度需求。
3) 在相同样本数据条件下,本文采用的QPSO-ELM方法辨识得到的某型涡轴发动机起动模型的精度要优于ELM、SVM和BP神经网络,能较好地解决解析法建立某型涡轴发动机起动过程模型难的问题。
由于发动机的起动范围较宽,针对高原、高空以及高低温等环境进行起动试车试验,获取更多反映不同大气条件下起动模型非线性特性的训练样本,建立该型发动机适用于整个起动包线的辨识模型,是值得进一步研究的。
