基于LSTM深度神经网络的精细化气温预报初探
2018-11-30倪铮梁萍
倪 铮 梁 萍
(中国人民解放军96873部队 陕西 宝鸡 721000)
0 引 言
天气与人类活动密切相关,随着科技发展和生活节奏的加快,准确精细的天气预报在日常生活、工作、国防与军队建设上起到越来越重要的作用。但是,气温要素的预报一直是天气预报中的重点和难点,本文利用LSTM神经网络,初步尝试精细化气温预报的模拟计算。
人工神经网络一直是气象预报的一种重要手段,但是由于BP神经网络的缺陷,其在气象预报业务方面的发展受到了极大制约。而近年来,人工神经网络在时间序列上的重大发展,使其在气象业务上有了重大突破。在时间序列分析中,未来的数据与过去的数据是相关的,但是普通BP神经网络并不能把这种相关性体现出来,而近年来出现的LSTM网络能很好地把这种相关性体现出来。并且在语音识别[8-9]、自动乐曲谱写[10]、自然语言学习[11]等领域已经有了重大应用,在气象领域也有LSTM结合CNN(Convolitional Neural Networks)进行临近降水预报的先例[6],还有研究表明通过LSTM神经网络建立的模型,能有效预报24小时和72小时的逐时次气温、湿度和风[1]。
1 循环神经网络和LSTM
图1是目前RNN运用的一种典型结构[5],RNN和传统的多层感知机的不同就是跟时间有了关系,下一时间的数据会受到上一时间数据的影响。图1的右边就是将左边展开的结果。
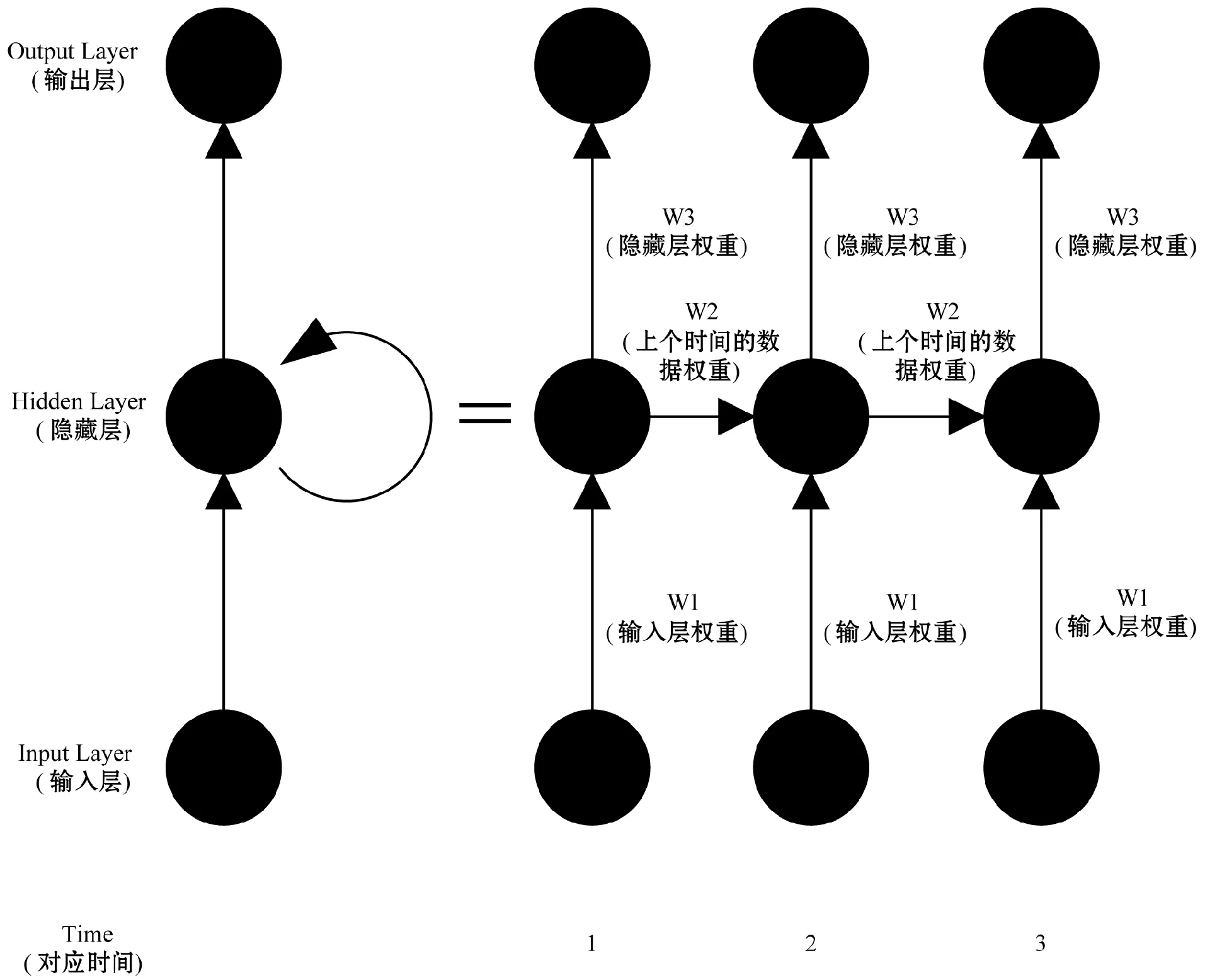
图1 典型的RNN结构
从图中的结构可以看出,一组时间序列(x1,x2,x3,…)的隐藏层和输出层将由如下公式计算得来:
(1)
(2)
与传统BP相比,RNN在隐层计算上多了过去时次数据作为输入,将未来的数据预报与过去数据比较紧密的联系起来,因此,更适用于时间序列预报。
1.1 RNN的梯度消失问题
原生的RNN会遇到一个很大的问题,叫作梯度消失(The vanishing gradient problem for RNNs)。对于传统深度神经网络来说,由于sigmoid函数的性质会导致反向传播过程中梯度消失,导致模型收敛速度过慢,训练时间加长。而对RNN来说,后面的时间节点对前面时间节点感知力下降,导致模型无法记住更久之前的数据,这也是原生RNN从20世纪80年代末提出以来,一直没有较大作用的原因。
但是,近几年,一种改进的RNN较好地解决了这个问题,这就是LSTM(Long-Short Term Memory)。
1.2 LSTM神经网络
LSTM的特点是可以记忆长时间的数据,因为它引进了一个核心元素Cell。Cell中有一堆参数state来记录过去的数据,但是有时候state参数并不是全部有用。比如,Cell中记录了过去1小时的气温,但在输入了当前时刻的气温后,相对于过去1小时的气温来说,当前时刻的气温更有价值。所以,为了表示这种关系,引入了一种遗忘机制Forget Gate。本文所使用的LSTM结构如图2所示。
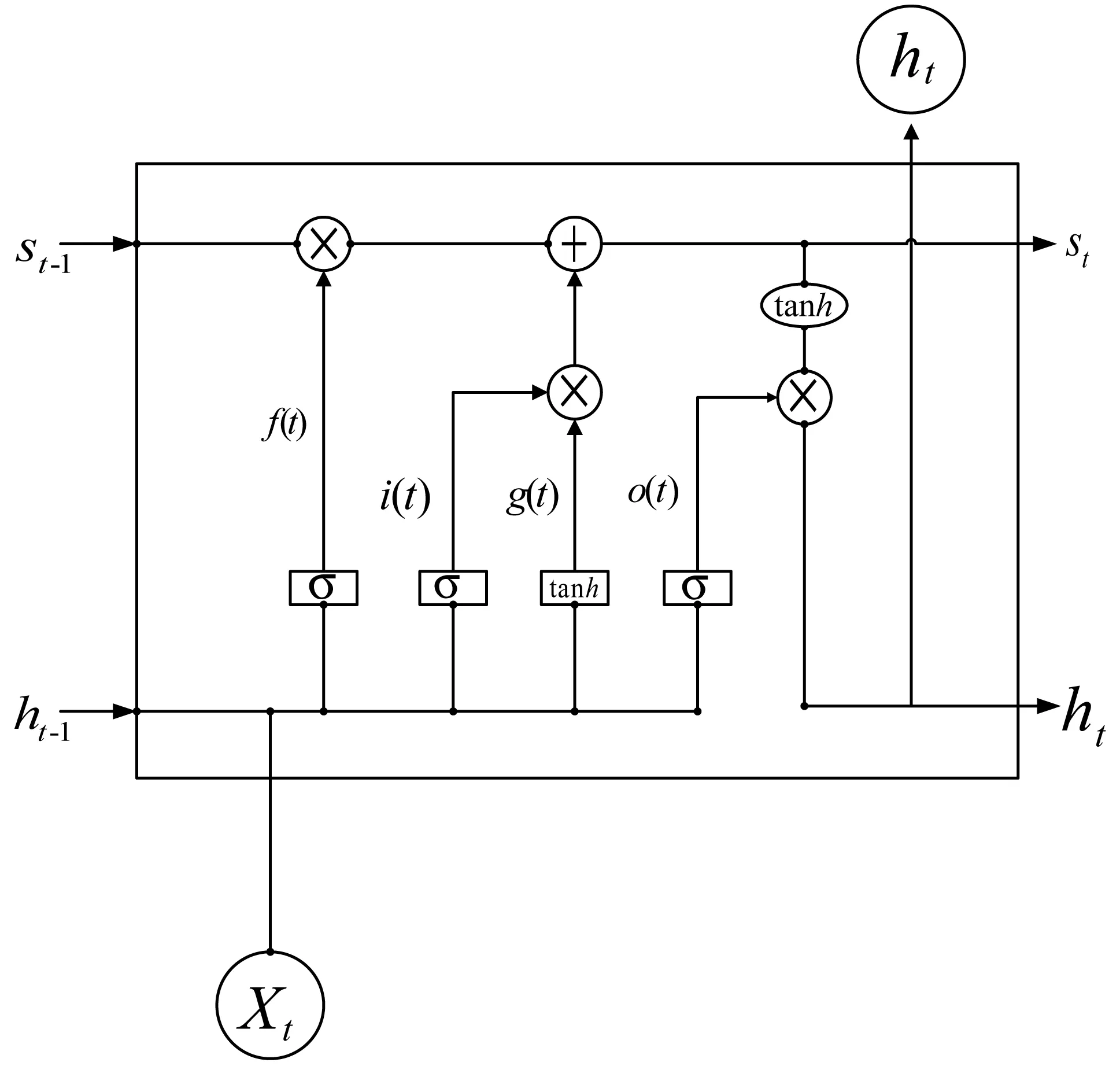
图2 本文所使用的LSTM结构
本文对LSTM网络的实现,主要参考了文献[5,10]对LSTM的公式描述,但是对其结构略有简化。
图2中s所代表的就是Cell的参数state;f(t)为Forget Gate方程;i(t)和g(t)共同构成了Input Gate方程,用来更新Cell状态s;o(t)是Output Gate方程,与s一起输出h。其方程如下:
f(t)=σ(Wf·[ht-1,xt]+bf)
(3)
i(t)=σ(Wi·[ht-1,xt]+bi)
(4)
g(t)=tanh(Wg·[ht-1,xt]+bg)
(5)
o(t)=σ(Wo·[ht-1,xt]+bo)
(6)
st=f(t)×st-1+i(t)×g(t)
(7)
ht=o(t)×tanh(st)
(8)
2 模 型
2.1 模型流程
如图3所示,所构建的模型为有两层LSTM隐层的网络。
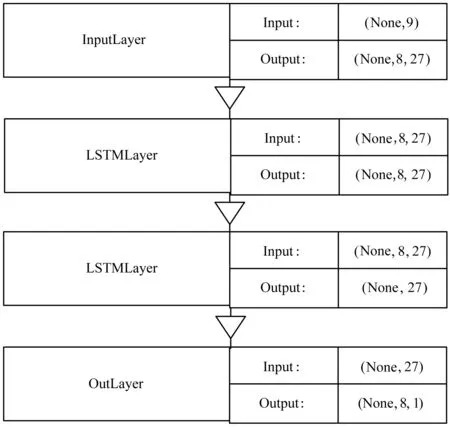
图3 模型流程及各层输入输出的数组形状
InputLayer:是一个全链接层,其输入数据为2维向量,第二维度是数据的特征;其输出也是一个2维向量(None,27),第二维度是隐层网络单元(在实验中并没有对节点单元数量进行控制,但是很多研究表明,寻找一个合适节点数是保证训练速度和训练效果的有效保障)。根据对LSTM的解释,为了能输入LSTMLayer,需要将其变为一个三维向量(None,8,27),增加的一维是时间步长(time step),在这个例子中就是说每8组数据构成一个时间序列。
LSTMLayer:LSTM层的具体结构如上文所述。第一层接受的输入为InputLayer的输出(None,8,27),其输出格式为(None,8,27),第二层接受的输入为第一层LSTM的输出(None,8,27),输出格式也为(None,8,27),但为了能进行输出层的输入,需要将其转为一个2维向量(None,27),去掉的维度是时间步长(time step)。
OutputLayer:是一个全链接层,其输入数据为LSTMLayer的Output,输出为预报值的2维向量。
2.2 要点解决方法
众所周知,人工神经网络的实现有两大难题,一是反向传播梯度下降过慢,二是过拟合,本文通过如下方法来抑制。
(1) 梯度下降问题 本文使用梯度下降优化器来解决这个问题。本文所使用的Adma优化器[4]依靠对梯度的一阶期望和二阶期望对学习率进行动态调整,目的是将一个固定的学习率变为一个动态的学习率。
(2) 过拟合 使用Dropout来防止过拟合。依据Srivastava等[2]对Dropout的解释,它能有效抑制过拟合。其主要思想是将每一个神经网络单元按照一定的概率暂时将其随机丢弃(Drop),因此每一次训练网络都是在训练不同的网络模型,这相当于是在训练多个模型进行组合。
3 数据训练及预报
3.1 数据说明及相关环境
训练数据:气温数据为宝鸡市2017年9月到2018年3月每日逐小时实况观测数据。高度场、涡度场、湿度场和温度场使用空军T511数值预报模式计算出的对应数据。每个时次太阳高度角和方位角数据是通过Python的PyEphem库计算的。其中,T511数值预报模式为每3小时一次预报。
验证数据:将2018年3月宝鸡市逐3小时气温作为验证数据。其特征数据为2018年3月T511数值产品、过去24小时气温、太阳高度角和方位角。输出为逐3小时气温预报,并与实况观测数据进行对比分析。
本实验使用Python作为开发语言,LSTM的构建使用Google的Tensorflow开源架构。
3.2 数据清洗
数据清洗流程如图4所示。
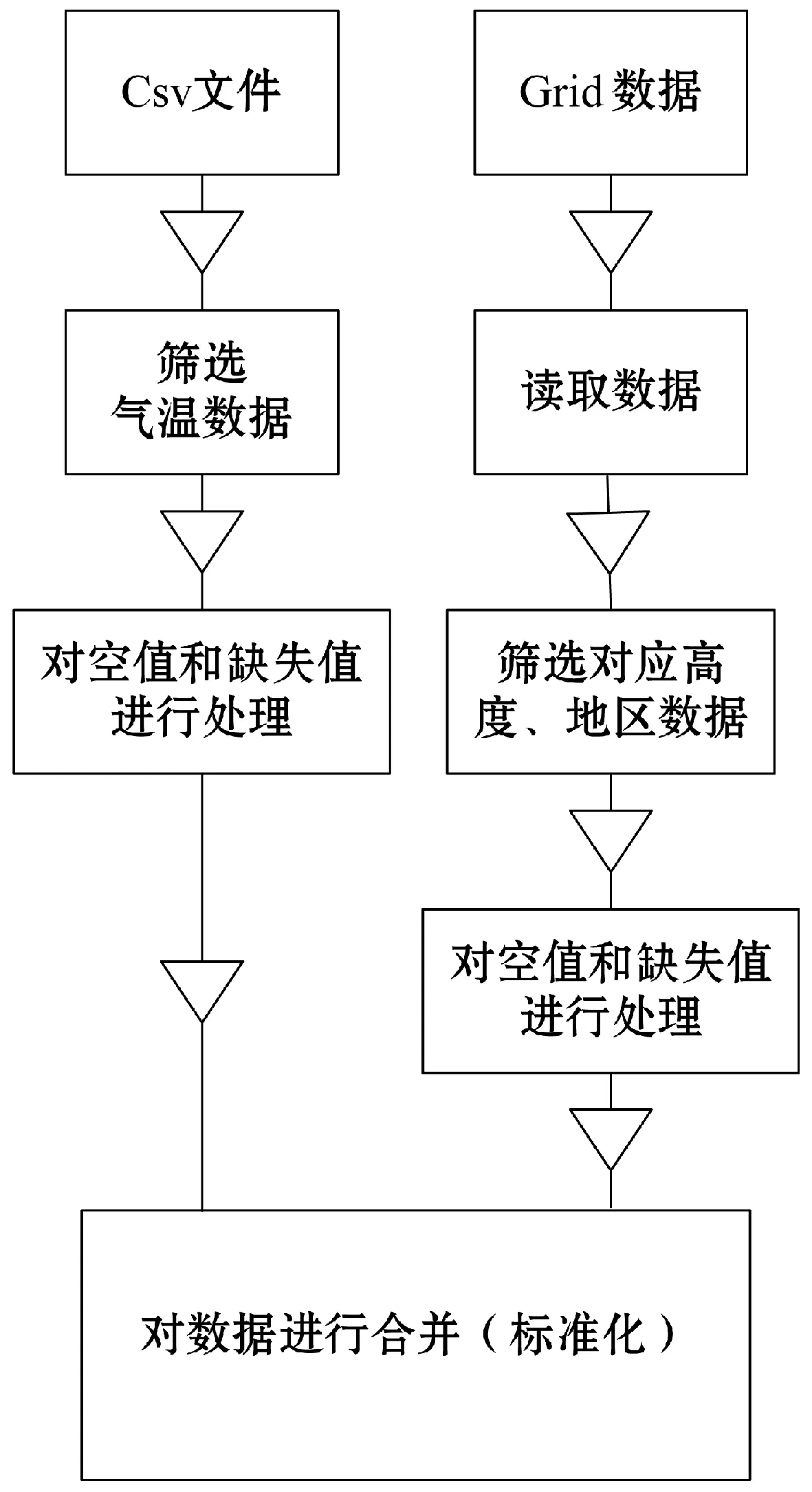
图4 数据清洗流程
对空值和缺失值的处理,并没有一种统一的做法,不同数据只能根据数据特点分别处理。本文中,为了体现数据的连续性将使用上一条数据与下一条数据的均值进行填充,公式如下:
Xt=(Xt-1+Xt+1)/2
(9)
3.3 特征要素选择
在实验中,主要对未来24小时的逐3小时气温进行预报。根据天气学原理, 气温除与历史气温相关外, 还主要与对流层中下部的气温、风、水汽含量等大气物理量有关。结合预报员的经验和气象工作者的长期研究,在数据特征选择中,主要选取了850 hpa温度场、850 hpa湿度场、700 hpa湿度场、850 hpa涡度场、700 hpa涡度场、2 m温度场。另外,为了表现局地的变化,还加上了太阳高度角和方位角。本文基于经验,初步选取了9个特征,并不排除有其他特征量对结果有较大影响,并且这9个特征在作为因变量时,相互之间也会有一定影响,这在一定程度上也会对结果产生一定偏差。
3.4 训练参数
参数初始化:对于输入层,对权重初始化为均值为0,标准差为1的标准正态矩阵;对输出层,初始化为0.1的常数矩阵;对LSTM层,从上面公式可以看出有s和h两个输出需要初始化,为了简单起见,直接初始化为0。
学习率:学习率经过多次实验,确定为0.001。
时间步长:时间步长可以设为一周、一个月甚至一年,随着时间步长的加大,可以学习到的数据细节可能会更多。但由于本文数据量和机器性能的局限,只把步长设为一天。
3.5 实验结果
所采取的预报模型如图5所示。
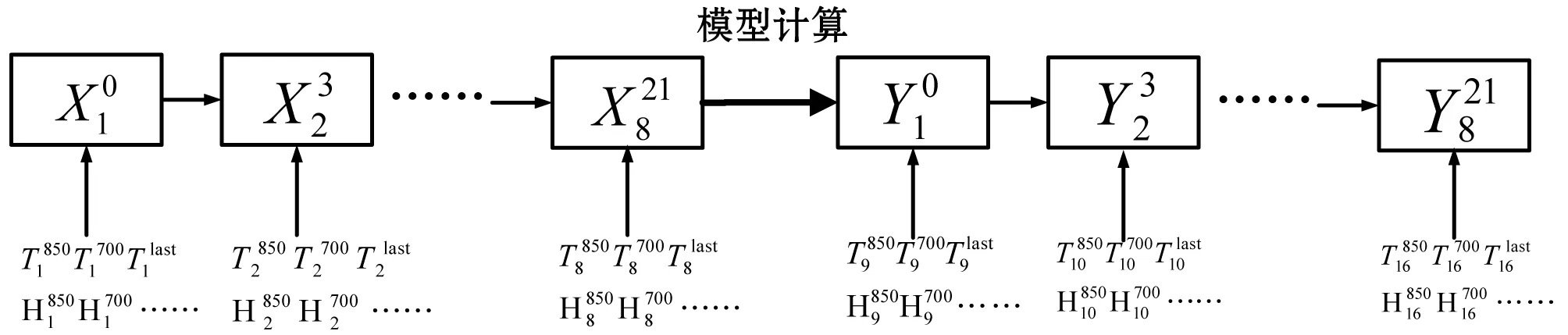
图5 预报模型
根据日常气象业务气温精细化预报的要求,当预报气温与实际气温之差小于等于2.0 ℃时,预报结果即为正确。所以本文所使用的预报准确率定义如下:
(10)
式(10)的含义是预报值与真实值差的绝对值小于等于2.0 ℃的个数与实际个数的比值,可以看到,模型效果越好,acc越接近1。
逐3小时气温化气温预报与实况的具体对比如图6所示,横轴为时间,单位是小时(h),纵轴是气温,单位是摄氏度(℃),实曲线为预报值,虚曲线为实况。结果表明:预报准确率为68.75%,日最低气温预报准确率为84.62%,日最高气温预报准确率为61.54%,预报值能较好地拟合实况。并且,从实况曲线中可以看到有两次天气转折的过程,这两次转折也在模型预报中体现了出来,说明LSTM神经网络结合数值预报产品能对天气转折进行较好描述。同时能较好地拟合实况也说明通过Dropout的方法可以避免过拟合的风险。
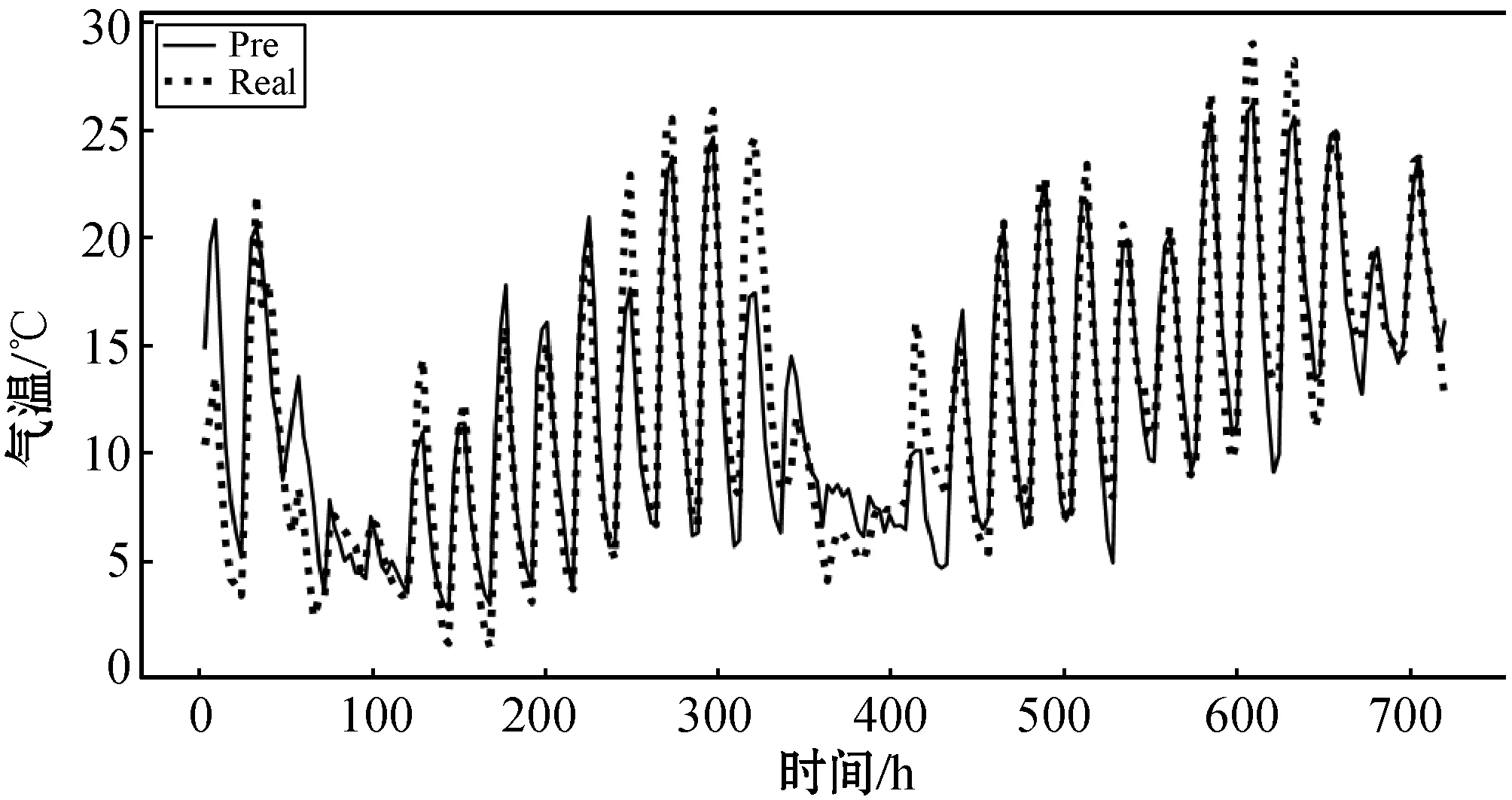
图6 实况与预报数据的对比
所训练模型对宝鸡地区2018年3月份的气温预报结果显示:
(1) 其气温预报预报准确率为68.75%,日最低气温预报准确率84.62%,日最高气温预报准确率61.54%,可以满足平时业务需要。
(2) 能较好地对转折天气的气温进行预报。
(3) 如果运用Optimizer和Dropout方法,能较好地解决神经网络收敛过慢和过拟合的问题。
4 结 语
本文运用了LSTM神经网络,对空军T511数据模式产品进行了试用,初步探索了LSTM网络在平时业务过程中的使用方法,并且发现其对气温预报的指导性较高,可以运用在平时业务过程中。
本文还存在选取的LSTM模型比较简单、训练数据过小,数据特征的选取没有依靠统计学原理等问题。这些问题对计算结果的影响有待进一步研究。
