涡轮叶片气膜孔结构化网格生成

张 祥 刘 勇 赵 璐 李亚清

(南京航空航天大学能源与动力学院航空发动机热环境与热结构工业和信息化部重点实验室 江苏 南京 210016)

0 引 言

涡轮是发动机中动力负荷与热负荷最大的部件，采用有效的冷却措施是发动机安全可靠工作的有效保证，也是降低高温材料成本的措施[1]。随着航空发动机性能发展的需求，涡轮叶片的冷却结构越来越复杂[2]。

工程上通常采用数值模拟技术预测涡轮叶片表面温度分布以计算分析热应力，从而预估其寿命[3]。在计算域的离散方面，结构化网格以其计算资源占用小、收敛速度快、求解精度高、适用于大规模并行计算等优点，在计算流体力学CFD(Computational Fluid Dynamics)领域具有不可替代的地位[4]。然而，由于涡轮叶型复杂的几何结构，其计算域结构化网格生成一直是数值模拟中的难点。在传统的网格生成过程中，通常采用现有商业软件生成非结构化网格或非结构/结构化混合网格，如Gambit、ICEM、HyperMesh等。即使采用全结构化网格，网格生成周期也十分漫长，而且能否生成结构化网格十分依赖工程技术人员经验。

为提高涡轮叶片网格结构化网格生成效率与自动化程度，缩短设计周期，本文在采用分块拼接网格策略[5-6]与遗传算法[7]的基础上，提出了一种针对涡轮叶片表面气膜孔的结构化网格生成方案。首先建立了分块质量评价函数，进而采用遗传算法寻求分区的最优方案，最终生成结构化网格。

1 分块质量评价函数与遗传算法

1.1 分块质量评价函数

目前，对于网格分区的质量评价大多依赖经验，常见的经验分区有针对圆孔特征的“O型分割”、针对三角特征的“Y型分割”(如图1所示)等。

(a) O型分割 (b) Y型分割 图1 常见结构化网格分区方案

分区结果的质量评价函数是分区过程自动化的基础。分块质量的好坏体现在对其生成的网格质量的影响上，而网格的质量体现在对CFD计算结果的影响上。通过理论分析及经验表明，CFD对网格的一般性要求为雅可比矩阵行列式的值大于0,其他指标包括网格扭曲、偏斜、翘曲等。本文在总结和借鉴众多现有商业网格生成软件网格质量评价模块的基础上，提出了拼接多块的质量评价指标。显然，当子分区为立方体时，所生成的网格质量最优，则该分区质量最好。所以，分块质量评价的根本目的就是确定分区与立方体的相似程度。依据评价指标计算是在表面面上进行还是在立方体上进行，将评价指标分为“2D评价指标”与“3D评价指标”。

1.1.1 2D评价指标

2D评价指标将在分区的各个表面上进行，主要计算指标有：翘曲角、偏斜度、扭曲度。

偏斜度(s)表征了该分区表面的尖锐程度，用四边形表面对边中点连线的夹角与直角的偏差来表示，如图2所示。归一化后为：

(1)

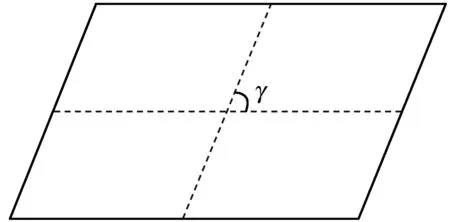
图2 偏斜度示意图

翘曲角(w)定义为：四边形表面对角线分割成的两个三角形的夹角的最大值，如图3所示。归一化后为：

(2)

图3 翘曲角示意图

扭曲度(t)表征了分区表面的扭曲程度，用四边形最大内角与最小内角中与直角偏差较大的角表示，如图4所示。归一化后为：

(3)

图4 扭曲角示意图

1.1.2 3D评价指标

面积比(a)表征了立方体与四面体的相似程度用相对表面面积比的最小值表示。a越小，该分区质量越差。

分区的雅可比矩阵行列式的值(J)反映了该分区与立方体的相似程度。如图5所示，根据文献[8], 假设Xm∈R3为六面体分区中的第m个顶点，Xm=[xm,ym,zm]T,m= 1,2,…,8。Xm,i∈R3(i=1,2,3)为与Xm共边的顶点，em,i=Xm,i-Xm(i=1,2,3)为第m个顶点的边向量的单位向量，则该分区某一顶点的雅可比矩阵Jm=[em,1,em,2,em,3]。

J=min[det(Jm)]m=1,…,8

(4)

图5 雅可比矩阵列向量示意图

式(4)中：J∈[-1,1]，J越大，则表明该分区与立方体相似程度越大。当J≤0，则认为该分区不成立。

1.2 气膜孔自动分区的遗传算法

针对气膜孔网格生成的分区问题，采用遗传算法来对分区结果寻优。得到分区结果后，采用超限插值算法生成结构化网格。根据文献[7], 遗传算法可以表示为：

SGA=(C,E,P0,M,Φ,Γ,Ψ,T)

(5)

式中：C为个体编码方法；E为个体适应度评价函数；P0为初代种群；M为种群大小；Φ为选择算子；Γ为交叉算子；Ψ为变异算子；T为遗传运算终止条件。

遗传算法在众多领域应用广泛，关于遗传算法的原理及流程本文不再赘述。需要指出的是，在染色体的编码与解码上，种群中每一个个体代表一种分区策略，用一个0到1之间的双浮点精度数的一维数组R表示分割点所在的位置，R=[r1,r2,…,rn],rj(j=1,2,…，n)。R代表了该分割点在其所在边上等分线段上的长度比例。以一个长度为32位的十进制整数的一维数组编码串对R进行编码。这样，就可以用一个十进制数组的集合完成对分区策略的编码。

例如：在长度为100的边上，染色体的表现型为R=[0.5,0.5,0.5,0.5],则该边分割形式如图6所示。

图6 染色体表现型示意图

针对自动分区问题，个体适应度函数取分区子块质量的最小值。这样，能够对上述评价指标逐一优化。

E=min[f(Bi)]

(6)

式中:

f(Bi)=min[w(Bi),s(Bi),t(Bi),a(Bi),J(Bi)]

i=1,2,…,nf(Bi)∈[-1,1]

(7)

终止条件设定为：当种群最大适应度与平均适应度之差小于10-5且各个分区的雅可比大于0时，终止计算。

终止条件可以表示为：

T=(Emax-Eavg)≤10-5∩J(Bi)>0

(8)

交叉概率与变异概率分别设置为0.75和0.1。

2 算例验证

通过计算涡轮叶片气膜孔的两种布置方案来验证上述分区方法的可行性。

2.1 平行气膜孔算例

平行气膜孔简化几何模型如图7所示，两直径为10的平行气膜孔布置在200×100×100的平板上，各边上的数字代表了边上的上下两表面对应边上的分割点的数目，两个圆上的分割点数均为4。

图7 两平行气膜孔几何模型

采用上述分区方法，种群个体数目为300，种群最大适应度收敛于0.439，遗传算法收敛曲线如图8所示。得到分区结果如图9所示。根据该结果，采用超限插值算法[9]生成结构化网格，网格尺寸设置为3.0，最终生成的网格结果如图10所示，网格数量为39 520。图11为z=50 mm平面上网格结果。

图8 平行气膜孔算例适应度收敛曲线

图9 平行气膜孔分区结果

图10 平行气膜孔结构化网格

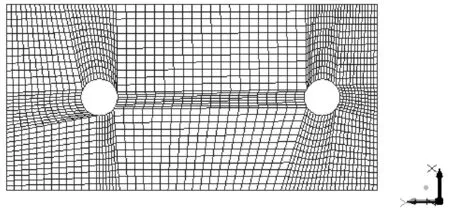
图11 z=50中心截面网格

将该网格结果导入ICEM进行网格质量评价。网格质量如表1所示。该分区结果表明：根据遗传算法寻优得到的分区结果生成的网格满足CFD计算需求。

表1 平行孔算例网格质量

2.2 交错气膜孔算例

交叉气膜孔算例简化几何模型如图12所示。两直径为10的气膜孔交叉布置在200×200×100的平板上，气膜孔法向分别为(1,0,1)、(0,1,1)。

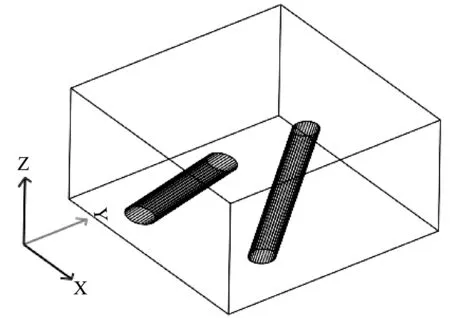
图12 交错气膜孔简化模型

采用上述遗传算法对该模型进行分区，各边分割点分布与平行气膜孔算例相同。种群数量为500，遗传算法进化374代，适应度收敛于0.209。遗传算法收敛曲线如图13所示。得到的分区结果如图14所示。同样采用超限插值法生成结构化网格，网格尺寸为3.0，网格数量为146 664，网格结果如图15所示。

图13 交错气膜孔算例收敛曲线

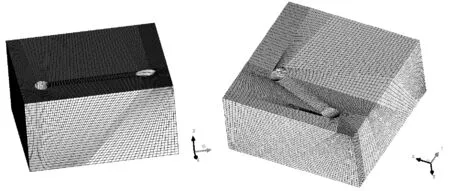
图15 交错气膜孔网格

将该网格结果导入ICEM进行质量评价。网格质量见表2。该网格质量满足CFD计算需求。

表2 交错孔算例网格质量

最后，对涡轮叶片整体生成结构化网格以验证该方法的可行性。整体叶片网格与气膜孔局部放大如图16所示。

图16 涡轮叶片整体网格

3 结 语

本文以涡轮叶片气膜孔为结构化网格生成的研究对象，采用多块拼接网格，结合遗传算法，并采用超限插值算法生成结构化网格。通过对涡轮叶片整体生成结构化网格以验证该方法的可行性。结果表明：本文提出的基于遗传算法的涡轮叶片气膜孔自动分区方法可以得到满足CFD计算需求的结构化网格。本文工作总结如下：

(1) 经检验，本文建立的分区质量评价函数能够反映分区的质量。网格质量与分区质量相关度较高。

(2) 遗传算法能够有效处理结构化网格分区问题。与传统手工划分网格方法相比，极大提高了网格生成的成功率与自动化程度。

(3) 在采用遗传算法分区前，需要预先设定对应面上的分割点数目，尚未解决全自动处理复杂几何结构分区的问题。