基于参数相关性分析的火电设备故障诊断方法
2018-11-29罗婵纯
罗婵纯
(大唐华银攸县能源有限公司, 湖南株洲 412307)
现代化工业技术的迅速发展下,火电设备不断走向大型化、集成化和自动化。火电设备的安全稳定运行,不仅直接关系到火电厂正常的发电生产,也会间接影响到电网的安全稳定运行。因此,火电重要设备一旦发生故障,造成的影响将十分巨大。为避免电力生产事故的发生,加强火电设备故障特征状态的早期识别显得尤为重要。设备在运行过程中,如果某个部件或零件出现了故障,相应的设备参数就会发生某些变化[1]。一个故障的发生,往往不仅仅只关系到某一个参数的变化,不同的故障模式下,相应参数的变化也各不相同,因此通过有效的分析方法实现对故障特殊参数的提取,是设备故障诊断过程中的重要环节。笔者主要运用数据相关性分析方法,对火电厂一次风机监测参数的历史数据进行分析,先对正常运行状态下的数据进行相关性分析。当设备异常或设备发生故障时,参数间相关关系将会发生改变[2]。因此,可根据正常与故障时参数相关性变化情况来发现和定位故障,为设备故障诊断提供依据。
1 相关性分析方法
相关性分析定义为对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。
1.1 Pearson相关系数
Pearson相关系数是研究两变量间相关性时最常用的方法,它需满足以下两个条件[3]:
(1) 必须假设数据是成对地从正态分布中取得的。
(2) 数据至少在逻辑范围内是等距的。
假设有两个变量X、Y,其Pearson相关系数求解公式如下:
(1)
式中:cov表示协方差;σ表示标准差;E表示期望;μX、μY分别表示X、Y的平均值。
1.2 Spearman相关系数
如果两个变量不满足Pearson相关分析的两个条件,可以采用Spearman相关系数来代替。
将变量X、Y分别按从小到大的秩次排序,重复的数据取它们次序的平均值,Spearman相关系数的计算公式如下:
(2)
式中:Ri、Qi分别是X、Y的秩次。
1.3 偏相关系数
在多变量情况下,两变量间的相关性往往容易受到其他变量的影响,为了得到它们之间真正的相关程度,可采用偏相关分析。
分析多个变量集合[X1,X2,…,Xk]中任意两变量之间的偏相关关系时,其计算是一个迭代的求解过程。
(3)
(4)
(5)
式中:r12.34…k为变量X1、X2在消除其他变量X3,…,Xk影响后的偏相关系数;rij为Xi和Xj之间的Pearson相关系数。
2 一次风机参数的相关性分析
一次风机是火电厂重要的辅助设备,主要为锅炉提供一次风,用来输送和干燥煤粉,并供给燃料燃烧初期所需的空气。为确保一次风机的正常稳定运行,机体主要安装了出力、振动、温度等类型的测点,具体分布见图1。
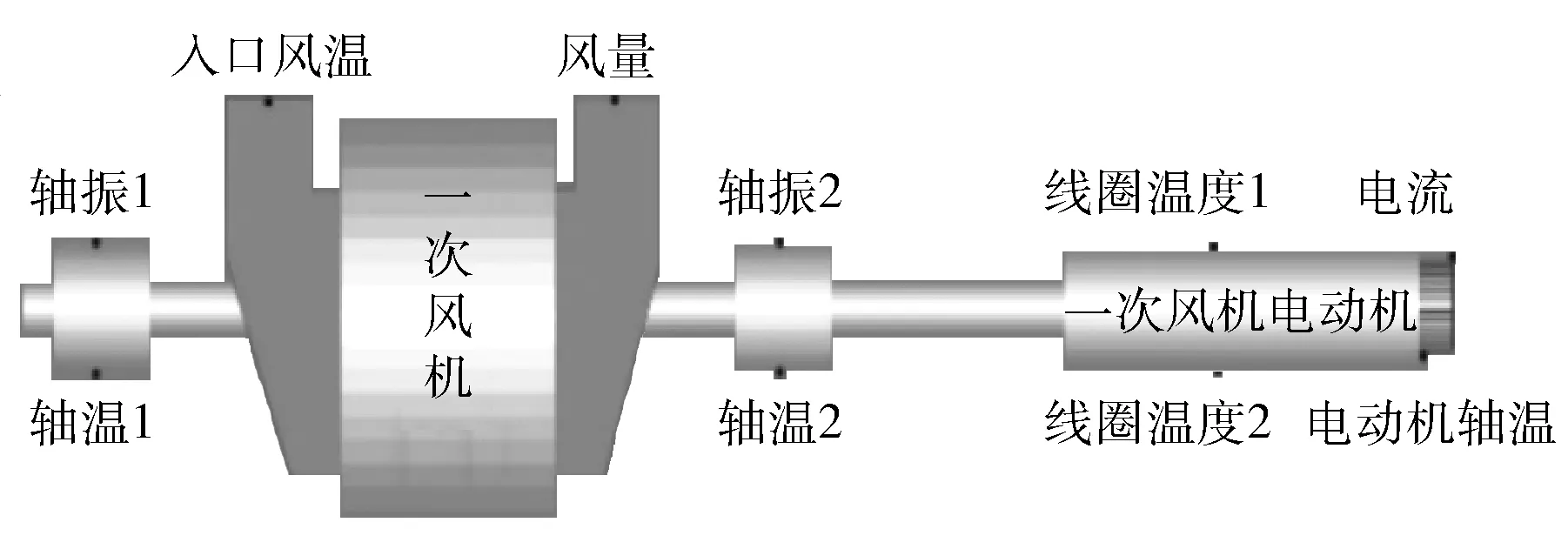
图1 一次风机测点安装分布图
选取一个月的一次风机正常运行历史数据(约1 000条)作为数据分析样本,见表1。
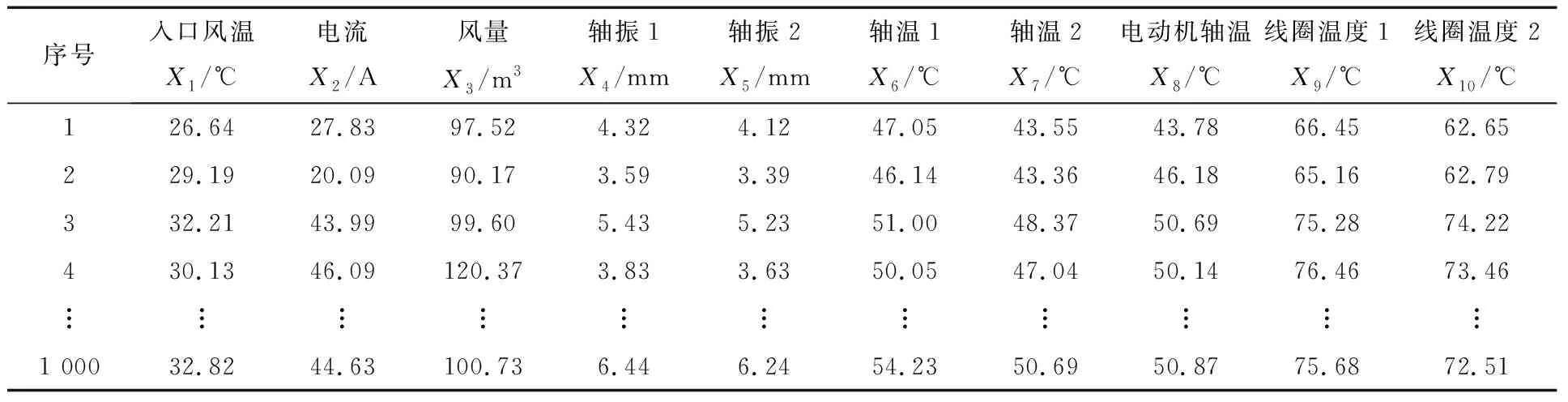
表1 一次风机主要测点
从表1可以发现:测点之间数量级有较大差异,不利于寻找各变量之间的关系。为了消除量纲影响,采用标准化方法对数据进行处理,该方法可以真实反映一个数据距离平均数的相对标准距离[3]。
(6)
i=1,2,…,n,j=1,2,…,m
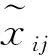
对一次风量任意两个变量间进行Pearson相关分析、Spearman相关分析和偏相关分析,得到相关系数分别见表2、表3和表4。由表2~表4可以看出:任意两个参量间Pearson相关系数和Spearman相关系数比较接近,而偏相关系数普遍较Pearson相关系数和Spearman相关系数要低。
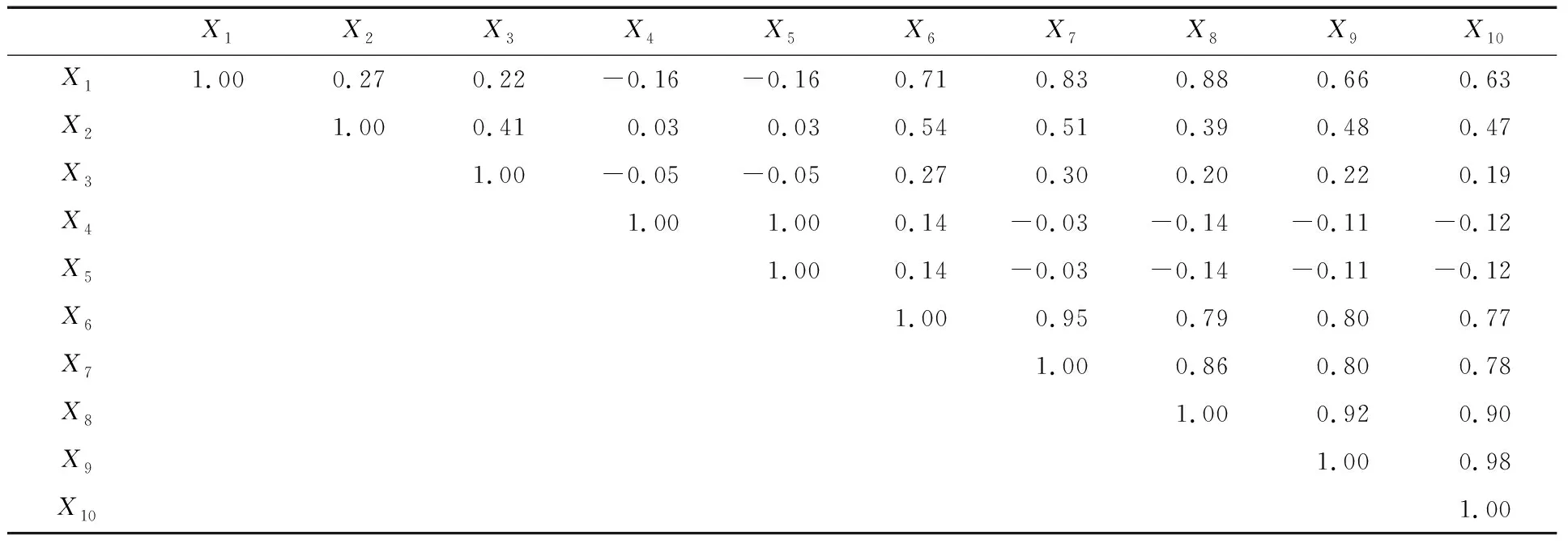
表2 Pearson相关系数
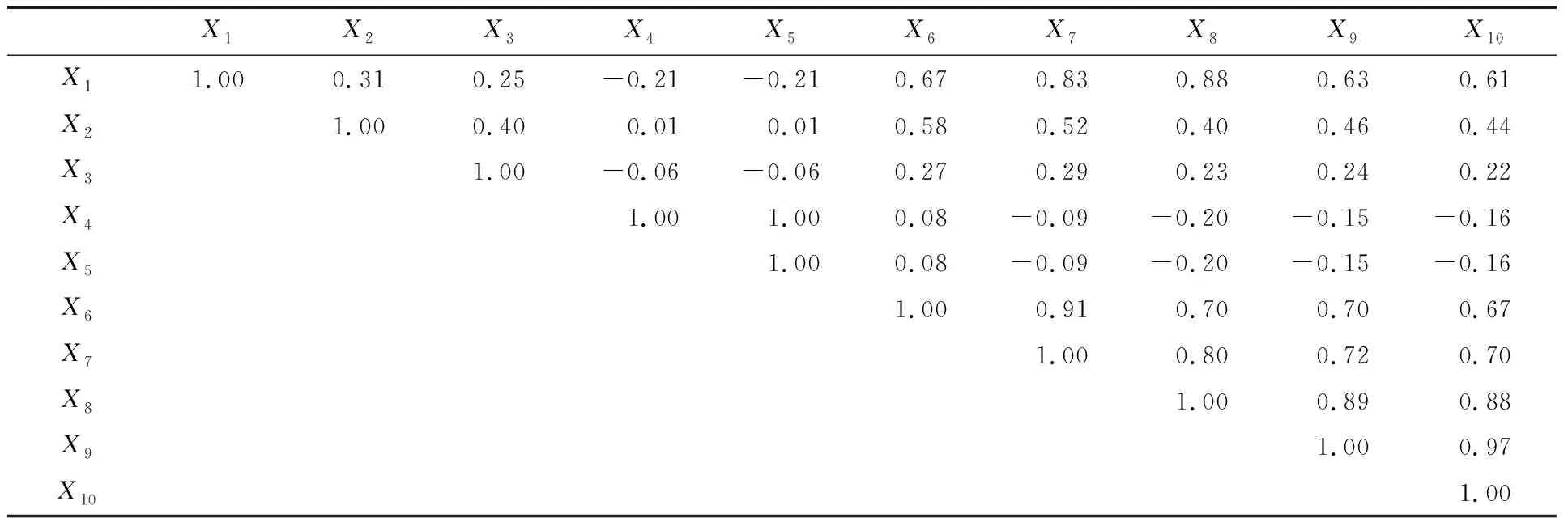
表3 Spearman相关系数
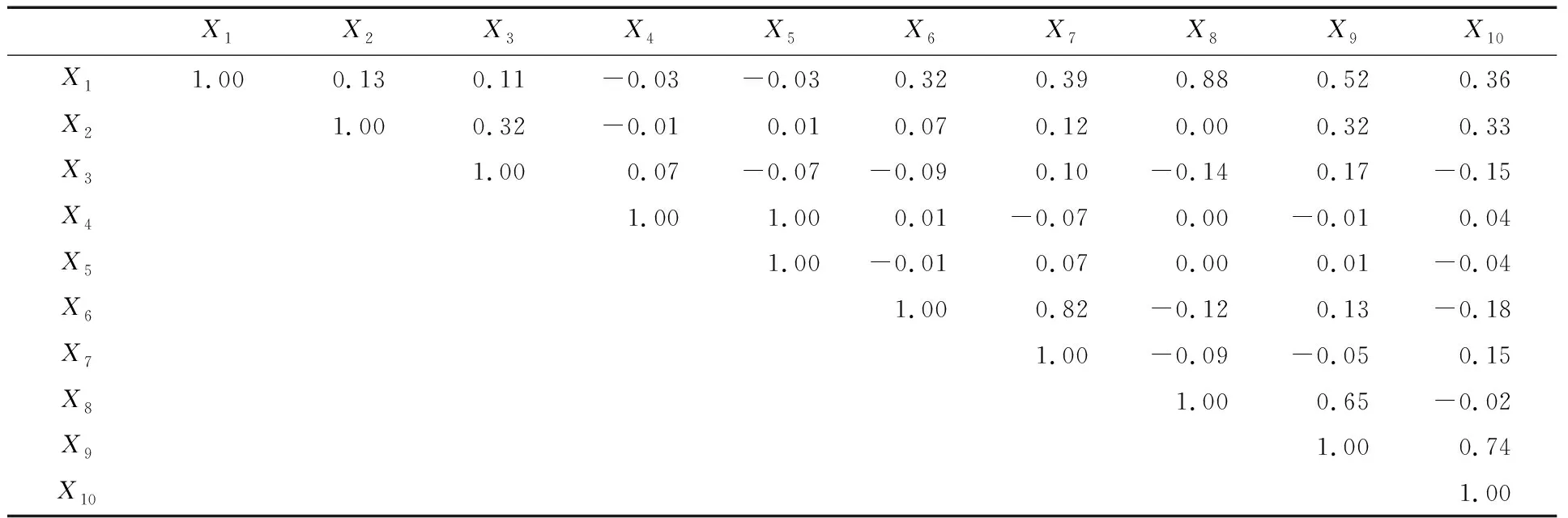
表4 偏相关系数
X4和X5(轴振1、轴振2)的相关系数均为1,说明两者存在很强的正相关性,即在同一刚性转子的振动耦合性强。同时,X6、X7和X8(风机侧轴温与电动机侧轴温)、X9和X10(线圈温度1和线圈温度2)的Pearson相关系数和Spearman相关系数均大于0.7,但偏相关系数却在[-0.15,0.15],这主要是因为偏相关系数排除了其他变量的影响,反映出两两测点的净相关性,更能表示两个变量之间的本质联系。因此,对火电设备参数间进行相关性分析时,偏相关分析更能反映两两变量之间的相关性关系,所以笔者在后续设备故障诊断分析过程中选择偏相关分析方法。
在计算变量间的偏相关系数后,可以对变量间是否存在显著的净相关进行推断[4]:
(1) 提出原假设,即两总体的偏相关系数与零无显著差异。
(2) 选择检验统计量。偏相关分析的检验统计量为t统计量,其数学定义为:
(7)
式中:r为偏相关系数;n为样本数;q为阶数。统计量服从n-q-2个自由度的t分布。当t分布的自由度很大的时候,t分布近似为标准正态分布,这里因为n很大,所以将统计量t视为服从标准正态分布。
(3) 计算检验统计量的观测值或对应的概率p。
(4) 决策。如果检验统计量的概率p小于给定的显著性水平α时,则应拒绝原假设,参数间存在显著相关性(取值1或-1);反之,则不能拒绝原假设。验证结果见表5。
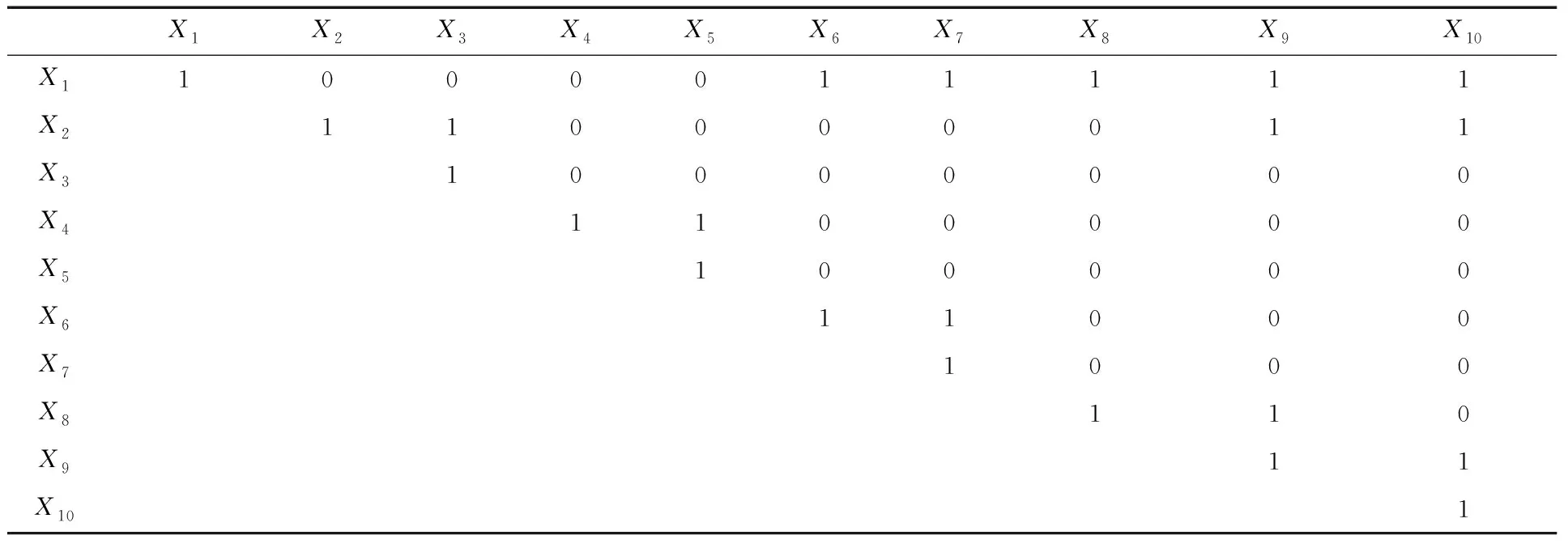
表5 相关性显著性验证
3 一次风机故障特征提取方法
通过表3的相关显著性验证发现了一次风机在正常运行时有如下相关性规律:
(1) 环境参数入口风温与温度类测点存在明显的正相关关系,即入口风温的增加的同时设备各温度测点也在增加。
(2) 电流与风量存在正相关关系。电流增加表示电动机负荷增加,负荷增加必会带来风量的增加。
(3) 同一部位的振动测点与轴温测点无明显的相关关系。
(4) 风机轴温与电动机轴温无明显相关关系。
当设备出现故障或者异常时,其参数间相关关系也会发生变化,可以通过正常运行时各参数之间的相关系数与异常时的相关系数对比发现故障特征参量,定位设备故障。
表6为一次风机异常状态下的相关性验证矩阵,阴影区域表示与正常运行时相关性显著验证矩阵存在不同。
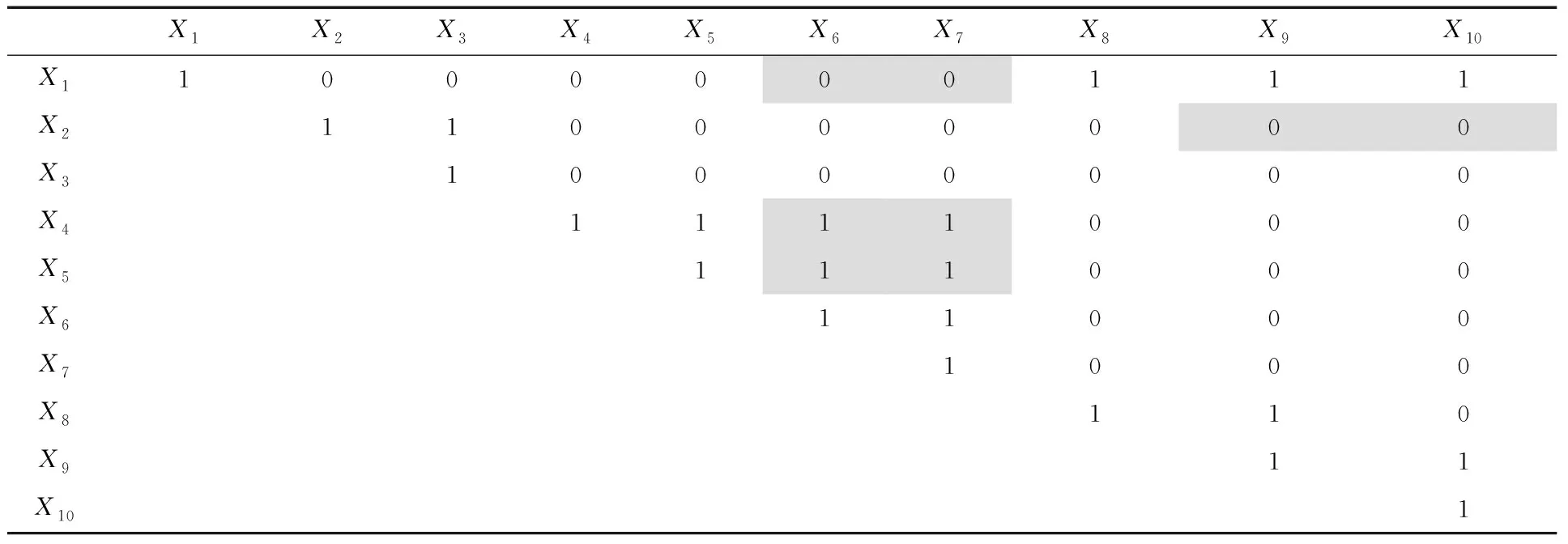
表6 设备异常状态下的相关性显著性验证
通过分析,发现入口风温对风机侧轴温的相关关系发生了变化,由正常时的显著性相关变成了不相关,即表示轴温上升并不受环境入口风温的影响,同时振动测点与轴温测点出现了显著性相关,由此可以定位设备异常可能来自于轴承座及辅助的润滑冷却系统,通过现场检查,发现润滑油品质变差,引起轴承润滑不良,导致振动加大且轴温升高。
表7为一次风机参数间相关性变化时可能存在的设备故障。
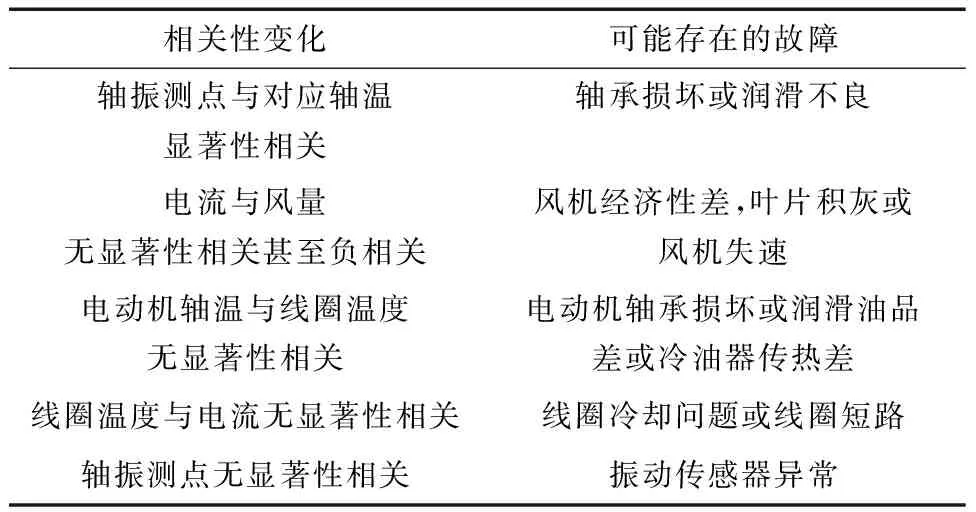
表7 参数相关性变化可能引发的故障列表
在运用相关性分析过程中,可提取设备正常运行数据进行参数间相关的训练学习,通过与计算机实时监测系统相结合,建立设备故障相关关系特征故障库,实时计算参量之间的相关关系,当参数之间的相关关系发生变化时匹配特征故障库,可以快速定位查找故障。
4 结语
(1) 相关分析方法中的偏相关分析相对Pearson相关分析和Spearman相关分析,剔除了其他参量对分析参量的影响,展现两两参量之间的净相关关系,能够更加清晰地用于设备故障分析和诊断。
(2) 通过参量间的显著性假设检验,可以确定参量之间的相关关系。在设备运行过程中,参量间相关关系较正常运行时发生了显著性变化,则反映设备可能存在的故障和异常,从而可以定位设备故障,为设备故障诊断提供依据。
