深井钻柱粘滑振动特性分析

，，，

(中国石油大学(北京)，北京 102249)

钻具在切割岩层时受到摩擦、压强、岩石质地等因素影响，经常会出现钻柱振动现象，造成严重的钻井问题，例如脱扣、跳钻、钻头的提前失效、较低的机械钻速以及BHA的失效等[1]。通常，钻柱振动被分为纵向、横向及扭转振动3种形式。本文研究的钻柱系统为旋转钻井系统，其广泛用于深层油气资源的勘探开发。在深井的钻井过程中，随着井深的增加，岩石硬度增加，塑性增加，地质条件更加错综复杂，并且随着钻柱长度的增加，钻柱的等效转矩刚度降低，传递转矩不足，在钻柱、钻头与井壁、井底的摩擦作用下，钻柱系统极易产生粘滑振动。钻柱粘滑振动被视为一种破坏性极大的扭转振动，将导致钻头及井下钻具的加速失效，严重影响钻井效率和钻井成本[2]。

1980年代，大位移钻井过程中出现的“粘滑”现象引起了钻井研究人员的注意，认为粘滑振动为扭转振动的一种特殊情况。1987年，Dawson等[3]从理论和试验研究了钻柱的“粘滑”现象，并与现场数据进行了对照，指出粘滑振动的滑脱状态是在钻头克服静摩擦阻力后出现的，其最大的转速可达常规转速的数倍；Kyllingstad和Halsey[4]通过建立简单的扭摆模型用以研究钻柱的粘滑振动，指出当钻柱发生粘滑振动时，钻柱的振动频率会低于扭摆的固有频率，同时转盘转速下降，当钻柱处于滑脱阶段时，钻柱底部最大转速至少是转盘转速的两倍以上，并提出通过减小钻压或降低转速可以有效抑制钻柱的粘滑振动； Challamel等[5]基于岩石破碎机理解释粘滑振动的基本原理，研究了钻头与岩石的相互作用对钻头的粘滑振动的影响；Richard等[6-7]通过钻头-岩石界面法则从钻头与岩石之间的摩擦接触和切削过程两部分对两种振动模式进行耦合，指出轴向和扭转振动的耦合是造成粘滑振动的根本原因，并对粘滑振动进行线性稳态分析及极限环分析。国内对于钻柱粘滑振动的研究起步较晚，研究成果也较少。黄根炉和韩志勇[8]将钻柱系统等效成集中质量摆，分析钻柱系统在钻头转矩以及钻柱与井壁的摩擦转矩作用下的稳定性，给出了钻柱产生粘滑振动的原因，分析了钻柱粘滑振动的影响因素并对顶部转矩负反馈减振法进行了讨论；牟海维等[9]通过建立粘滑振动的扭摆模型，得出钻柱粘滑振动的力学规律，分析了钻柱长度对粘滑振动的影响；韩春杰等[10]通过建立大位移井钻柱的等效扭转摆模型，分析了在钻头与地层转矩及钻柱与井壁间摩阻转矩作用下钻柱的动态行为，指出粘滑振动是钻头克服摩阻转矩的结果；祝效华、汤历平等[11]通过建立钻柱集中质量扭摆模型，研究了深部地层钻头的粘滑振动特性和发生振动时钻头的运动规律。

目前，学者在研究钻柱系统粘滑振动特性时大多数采用了速度弱化摩擦模型来考虑钻头与地层间的相互作用。在这种方法中，认为粘滑振动是由钻压与地层的摩擦作用引起的，而速度弱化是由钻头与地层间的固有特性决定的，忽略了钻头的几何特性，也没有考虑钻头切削作用的影响。本文探讨当摩擦因数为常数，引入轴向自由度，考虑钻头的切削作用，系统是否会出现粘滑振动；分析了粘滑振动时系统钻井参数对粘滑振动的影响，为实际工程中抑制钻柱粘滑振动提供理论参考。

1 钻柱系统力学模型

旋转钻井系统主要由井架、钻柱、钻头3部分组成。其中钻柱由BHA和钻杆组成，BHA是由重型钢管组成，以向钻头提供一个较大的钻压，而钻杆是由轻型钢管组成。为了便于对钻柱粘滑振动的研究，将振动模型进行简化，给出如下假设：所研究的钻柱系统位于垂直井中；忽略钻头的横向振动[6]。

钻柱简化的集中参数模型如图1所示，Kt、Ka分别为钻杆的等效扭转刚度、等效轴向刚度，Ct、Ca分别为扭转粘性阻尼、轴向粘性阻尼，I和M分别为BHA的等效惯性矩和等效集中质量。钻柱的顶端施加的轴向恒力H0代表大钩载荷，恒定的角速度Ω0代表上部转盘驱动转速。

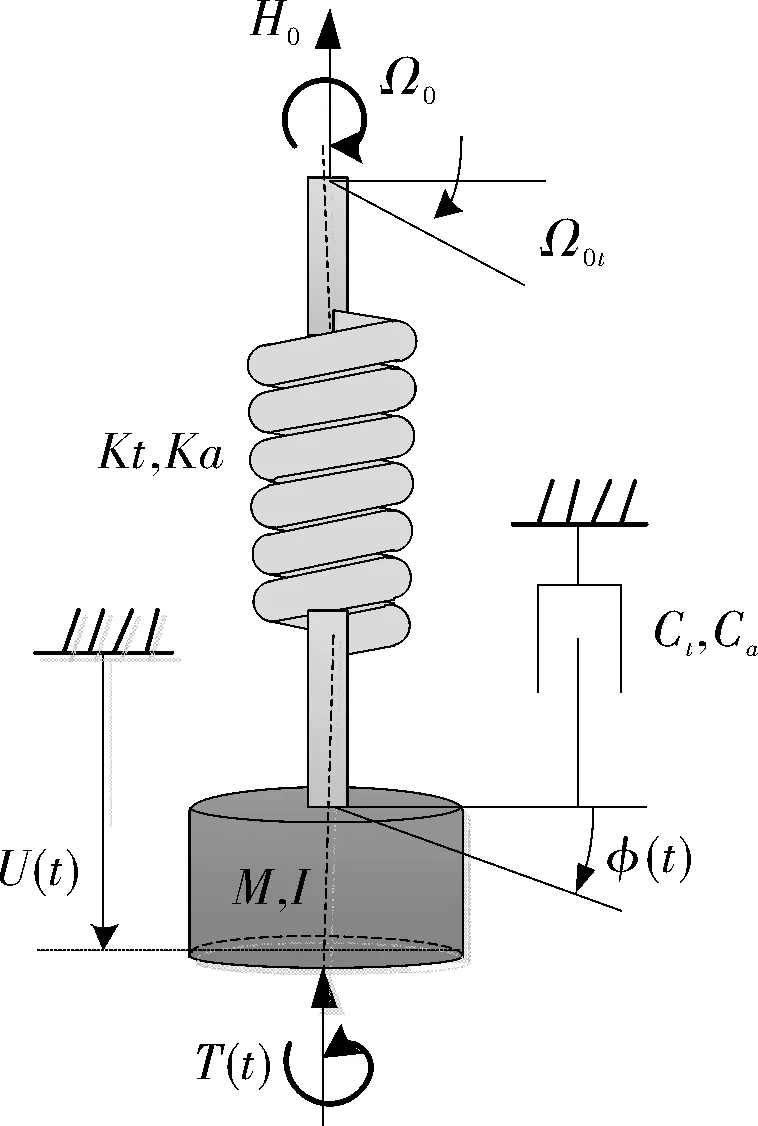
图1 钻柱系统轴向-扭转耦合简化模型

根据拉格朗日原理，推导出钻柱系统轴向-扭转耦合动力学控制方程为

(1)

(2)

式中：W0为正常钻进时钻头的钻压。

1.1 钻头与岩石相互作用法则

为了研究钻柱系统的轴向-扭转耦合振动特性，引入钻头与岩石相互作用法则。首先以持续稳定破岩的单刀翼作为研究对象(如图2)，钻头的切削运动由2个独立过程组成：①发生在切削面的切削过程；②岩石与摩擦底面间的摩擦接触过程。Fc为刀具作用于切削面的切削力的合力，Ff为作用于摩擦底面的摩擦力的合力，分别将其沿水平方向(下标为s)和垂直方向(下标为n)分解，切削力与摩擦力可分别表示为[7]

Fcs=εwd，Fcf=ζFcs，Ffs=μFfn，Ffn=σwl

(3)

式中：ε为岩石的固有比能；ζ为与切削力方向相关的特征量；μ为摩擦因数；σ为摩擦面的最大接触压力；d为刀翼的切削深度；w为钻头切削刀翼宽度；l为摩擦底平面的长度。

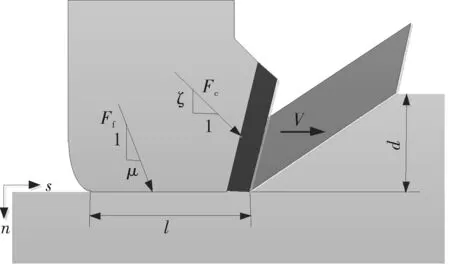
图2 单刀翼受力分析简图

转矩T与钻压W可以被分解为切削与摩擦两个分量，分别为Tc、Tf和Wc、Wf，即

T=Tc+Tf，W=Wc+Wf

(4)

钻头所受转矩和钻压的切削分量分别表示为

(5)

式中：a为钻头半径。

钻头所受转矩和钻压的摩擦分量间的关系可表示为

2Tf=μaγWf

(6)

式中：γ表征为不同结构形状钻头的轴向载荷和切削载荷之间的关系，是钻头空间分布特性的几何参数，其取值一般大于1。

钻头破岩的临界摩擦分量可表示为

(7)

假设钻头不存在横向振动，PDC钻头由n片相同刀翼组成，且每两片刀翼之间的夹角均为2π/n。当钻头钻进时，每个刀翼的切削深度dn相同，dn可以根据钻头的轴向位移U求得[12]。

dn(t)=U(t)-U(t-tn)

(8)

其中，时滞tn是钻头转动2π/n所需的时间，由式(9)确定。

φ(t)-φ(t-tn)=2π/n

(9)

钻头的等效摩擦长度和整个钻头的切削深度可表示为l=nln，d=ndn。

假设在正常钻进条件下，摩擦转矩足够大，可以抑制钻头的反向转动，因此在tk时刻钻头粘滞的条件为：

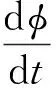
(10)

在粘滞阶段，顶部转盘依旧转动，钻柱因扭转不断积累转矩T=K(φ-Ω0t)，当钻柱所积累的转矩足以克服切削岩石所必要的转矩(Tc+Tf)，此时钻头开始滑动，其滑动时刻tp可由式(11)求得。

(11)

其中，φk=φ(tk)，dk=d(tk)。

2 控制方程求解

2.1 无量纲参数的提出

钻柱系统稳态钻进时有16个控制参数：BHA等效集中质量M和转动惯量I，钻杆的等效扭转刚度Kt、等效轴向刚度Ka，扭转粘性阻尼Ct、轴向粘性阻尼Ca，地层的固有比能ε，与切削力方向相关的特征量ζ，与地层内摩擦角相关的摩擦因数μ，刀翼与岩层接触界面的最大接触压力σ，摩擦底平面的长度l，钻头半径a，钻头的几何参数γ，钻头刀翼数n，稳态钻压W0，稳态转矩T0。为了方便进一步研究粘滑振动的特性，有必要减少物理参数个数，在此引入反映钻柱结构总体响应的时间尺度和体现钻头与地层相互作用的长度尺度。

(12)

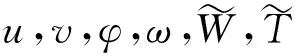
(13)

同样，定义无量纲切削深度

(14)

以上所有变量都是关于无量纲时间τ的函数，τ可定义为：

(15)

设钻头的切削深度为

(16)

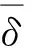
(17)

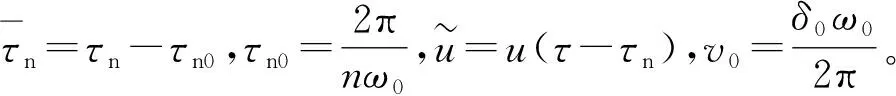
根据式(9)可推导出扰动时滞的代数方程如式(18)。

(18)

2.2 无量钢控制方程

根据钻头与地层相互作用法则，可得到钻柱系统无量纲化动力学控制方程。

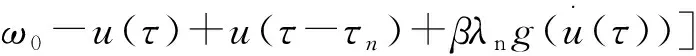
(19)

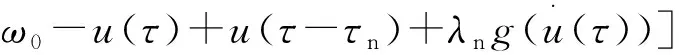
(20)

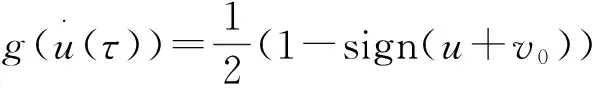
关于钻头几何特征、磨损状态、钻柱结构的集中参数、钻柱系统轴向阻尼比、钻柱轴向与扭转固有频率、扭转阻尼比可分别表示如下：

(21)

3 轴向-扭转耦合系统无量纲参数影响分析

钻井过程中的钻柱系统是一个非常复杂的系统，根据钻柱的工作环境及钻头的运动方程可知，钻头的几何结构、钻柱的结构与钻压、转盘转速、粘性阻尼等因素均对钻柱系统的粘滑振动产生影响。本文将详细分析钻头角速度、钻压、钻柱系统粘性阻尼比、钻头刀翼数对粘滑振动的影响。

钻柱系统无量纲化参数如表1所示。

表1 钻柱系统无量纲参数

3.1 建立仿真模型

利用建立的控制方程，采用Simulink模块对单自由度系统振动模型进行控制仿真，仿真框图如图3所示。采用Variable Time Delay模块实现时滞。控制方程由MATLAB function模块实现，通过MATLAB 编程链接到Simulink当中。采用变步长四阶/五阶龙格库塔积分法，并设相对误差限为1×10-3。

3.2 钻柱系统控制参数对粘滑振动的影响

3.2.1角速度的影响

钻头处于粘滞时刻时，钻头滞后于转盘的角位移不断增加，其增速主要是由转盘转速确定。因此，角速度ω0必然对粘滑振动产生影响。为研究角速度ω0对粘滑振动的影响，表1中其他参数不变，只改变转盘角速度ω0的值，ω0的取值分别为3.0、4.0、4.5、5.0。

不同转盘角速度ω0下钻头角速度时程响应曲线如图4所示。由图4可知，当角速度ω0为3.0、4.0、4.5时，钻柱系统发生了粘滑振动，而角速度ω0为5.0时，钻头角速度始终大于0，没有形成粘滑振动。由此推断，过小的角速度ω0会导致粘滑振动的发生，并且系统存在临界角速度，使得角速度ω0小于该临界值时粘滑振动产生；而角速度ω0大于该临界值时粘滑振动并不产生。在角速度ω0增大到粘滑振动失效之前，随着角速度ω0的增大，钻头粘滞阶段时间减小，但钻头在发生滑脱过程中所能达到的最大角速度在不断增大，且可达到转盘角速度的2～3倍，钻头的振动加剧。因此，可以通过提高转盘转速来抑制粘滑振动，但现场试验数据分析表明，随着转盘转速的增加，机械钻速会出现先增加后降低的趋势，尤其是在遇到可钻性较差的地层时钻速过高，会导致钻齿与井底接触时间变短，从而出现钻速降低，钻井效率降低的现象。在实际钻井过程中不可一味的提高转盘转速来抑制粘滑振动的发生。

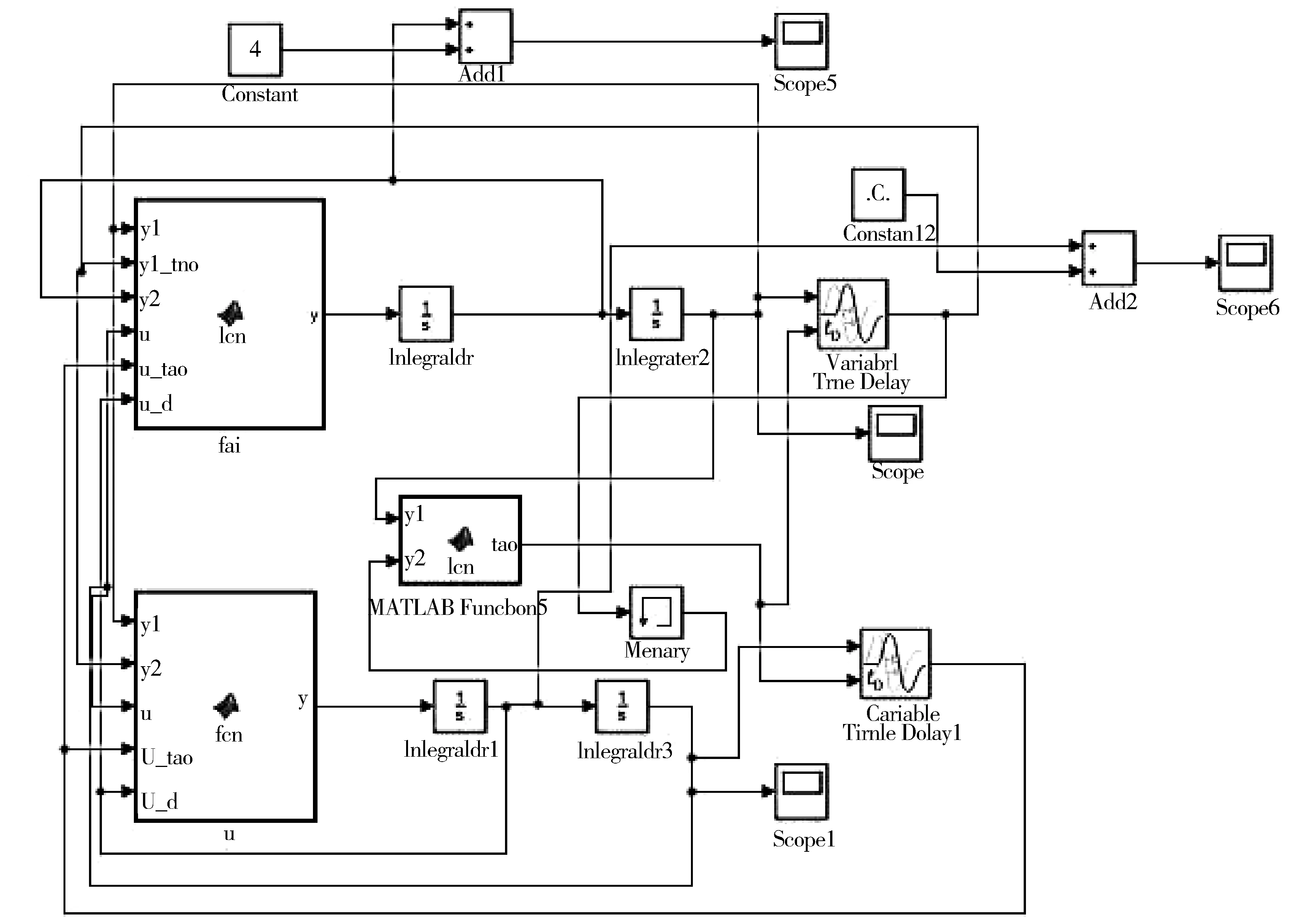
图3 Simulink仿真框图

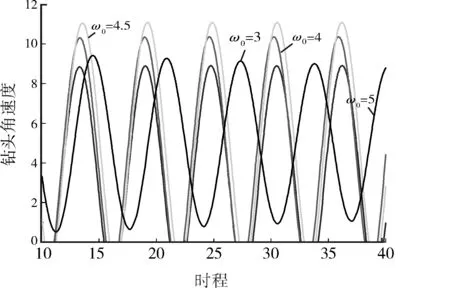
图4 不同角速度ω0下钻头角速度时程响应曲线

3.2.2钻压的影响

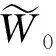
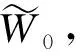
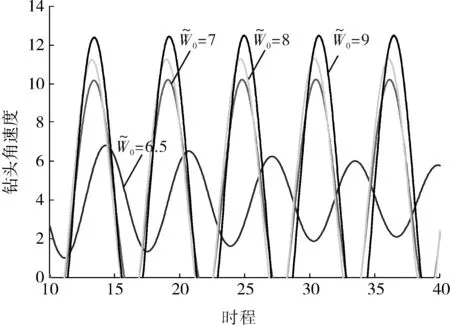
图5 不同钻压下钻头角速度时程响应曲线

3.3 钻柱系统结构参数对粘滑振动的影响

3.3.1粘性阻尼的影响

保持表1中其他参数不变，只改变阻尼比κ，ξ的大小，研究粘性阻尼比对粘滑振动的影响。所选取轴向阻尼比等于扭转阻尼比，即κ=ξ，分别为0、0.02、0.04、0.05。

不同粘性阻尼比下钻头绝对角速度时程响应曲线图6所示。由图6可知，并非所有粘性阻尼比情况下都会产生粘滑振动，当阻尼比为0、0.02、0.04时，钻柱系统发生了粘滑振动，而当阻尼比增大到0.05时，钻头粘滑振动现象消失。由此推断，系统存在临界阻尼比，使得阻尼比小于该临界时，粘滑振动产生；而阻尼比大于该临界值时，并不产生粘滑振动。从图6中还可以看出，当系统粘性阻尼比逐渐增大时，钻柱系统的振幅逐渐减少，钻头处于粘滞阶段的时间也逐渐减少。增大粘性阻尼系数，在一定程度上可以减缓或者抑制钻柱系统粘滑振动的发生。

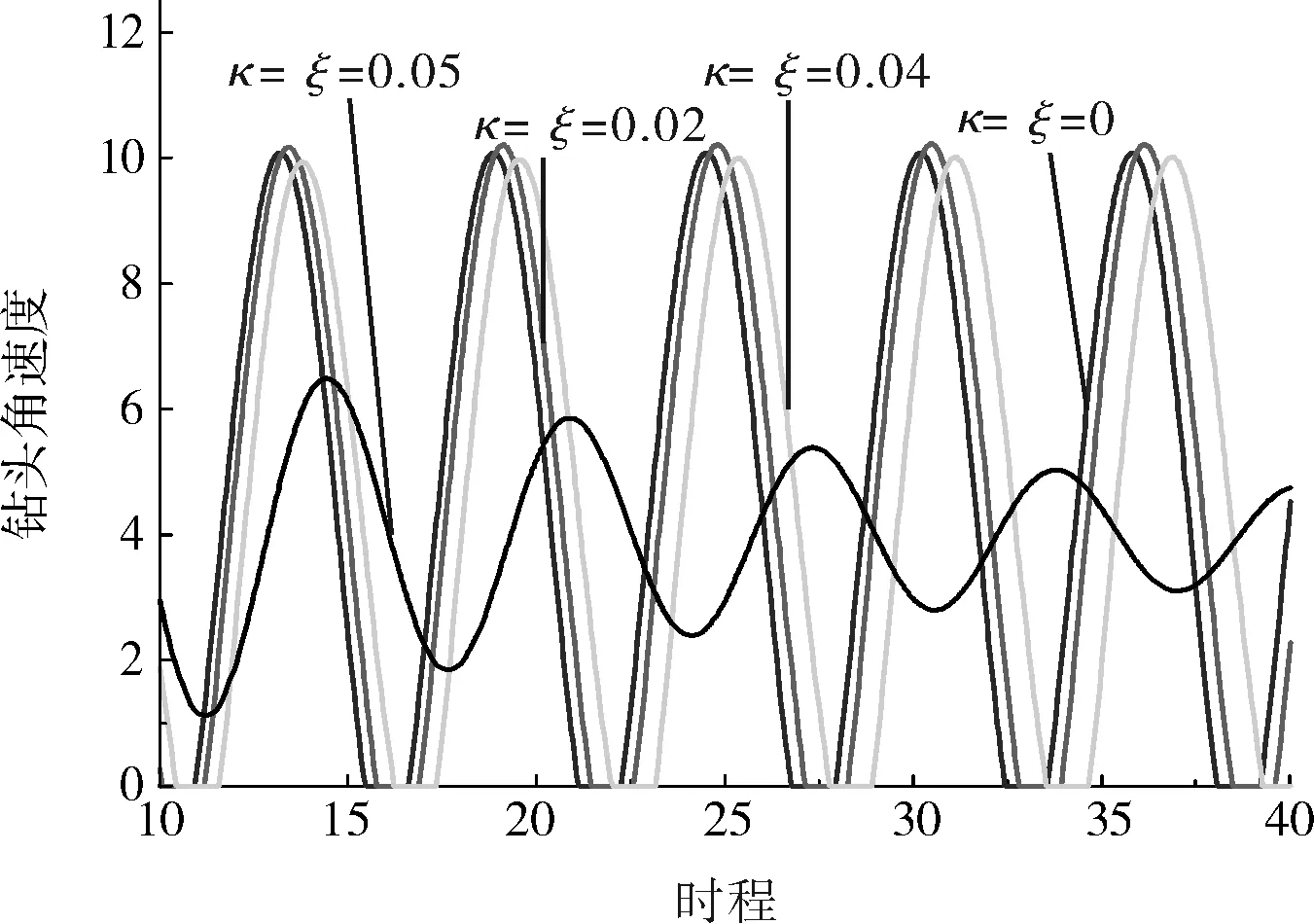
图6 不同粘性阻尼比下钻头角速度时程响应曲线

3.3.2刀翼数的影响

由式(9)可知，钻头的刀翼数n将对时滞tn和钻头切削深度产生影响，刀翼数n较少时，时滞tn较大，钻头的切削深度较少。同样保持表1其他参数不变，改变钻头的刀翼数n，研究钻头刀翼数对粘滑振动的影响，刀翼数n分别取4、6、8。

不同刀翼数下钻头角速度时程响应曲线如图7所示。随着钻头刀翼数的增加，钻头处于粘滞阶段的时间减少，钻柱系统的振幅也随之减少。当刀翼数增大到6时，钻头粘滑振动现象消失。合理选择较大的钻头刀翼数在一定程度上可以减缓或者抑制钻柱系统粘滑振动的发生。

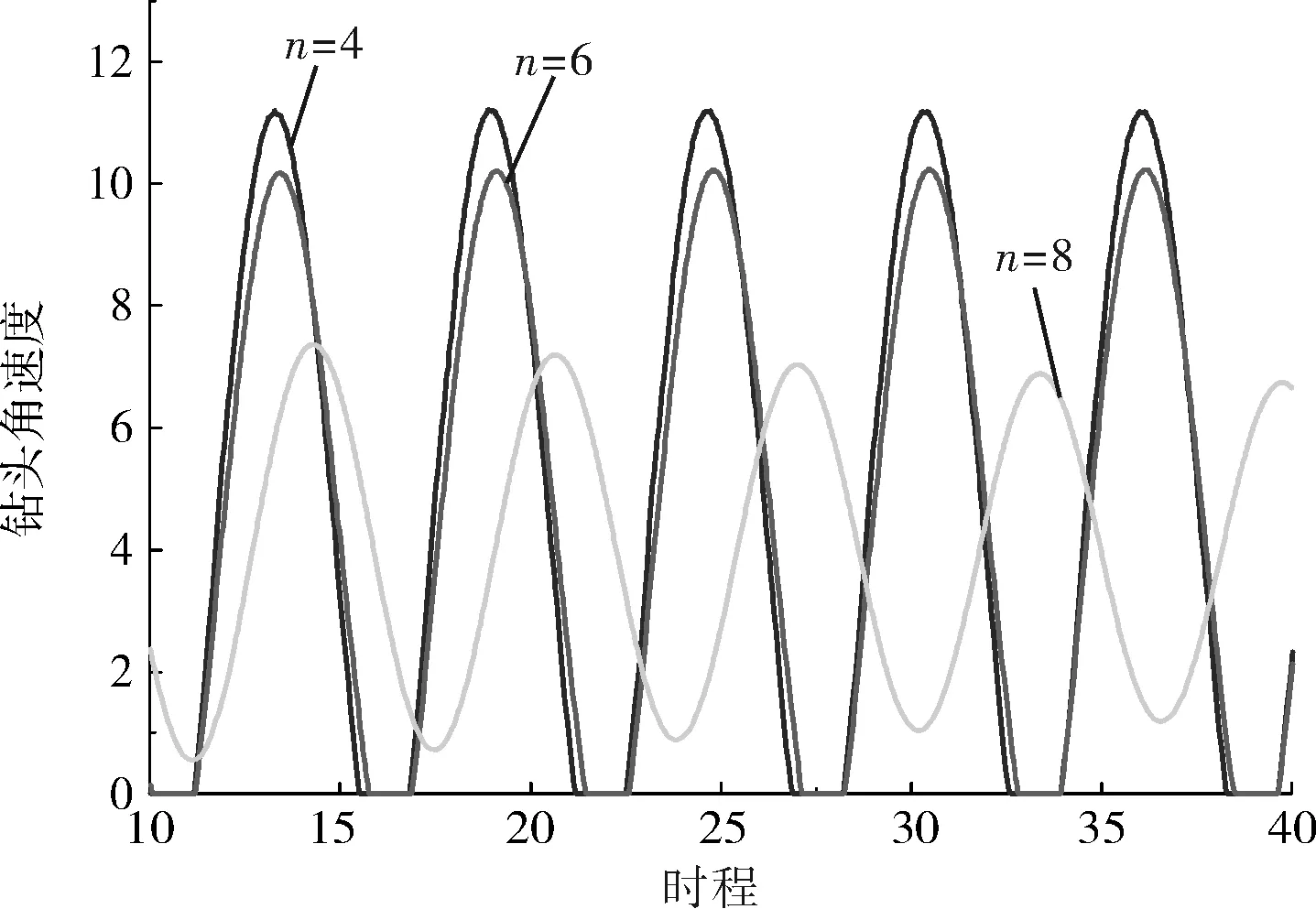
图7 不同刀翼数下钻头角速度时程响应曲线

4 结论

1) 通过对钻柱系统合理的假设和简化后，考虑轴向-扭转两种模式建立旋转钻井系统集中质量模型。采用的钻头与地层间的相互作用模型中，既考虑了摩擦过程，又考虑了切削过程，并通过切削过程将轴向与扭转模式耦合起来，引进了无量纲参数，并得到了无量纲控制方程。

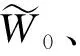
3) 在一定的钻井参数下，钻柱系统在转盘转速较低时会发生粘滑振动，转盘转速越低，粘滑振动越激烈；钻柱系统存在发生粘滑振动的临界值，当转盘转速不断增大到临界值时，钻柱系统粘滑振动消失。

4) 在一定的钻井参数下，钻柱系统在钻压较大时容易发生粘滑振动，钻压越高，粘滑振动越激烈；钻柱系统存在发生粘滑振动的临界钻压，当钻压不断减小至临界值时，粘滑振动不断减弱直至消失。

5) 在一定的钻井参数下，粘性阻尼比对粘滑振动产生影响，阻尼比越小，粘滑振动越激烈。钻柱系统存在发生粘滑振动的临界阻尼比，当阻尼比增大到临界值时，钻柱系统粘滑振动消失。增大粘性阻尼比，有利于减弱或抑制粘滑振动的发生，但是增大粘性阻尼，比会加大钻柱系统的能量耗散。

6) 钻头的刀翼数对粘滑振动产生影响，当系统发生粘滑振动时，增加刀翼数，可能会减弱或抑制粘滑振动现象，减少刀翼数，粘滑振动更加激烈。