基于气象水文耦合的中小河流枯季径流短期预报
2018-11-29王东升
王 东 升
(云南省水文水资源局,昆明 650106)
0 引 言
在水文预报中引入降水预报信息,采用气象水文耦合方法延长预报预见期,可为防汛减灾、水资源调度、水力发电、生态环境保护提供重要依据,赢得更多的应急响应时间,是近年正在形成和发展的水文预报分支,是未来水文预报发展趋势[1-3]。张建云院士提出,需要加强水文气象的学科交叉和结合,开展定量降水预报(QPF)的研究和应用,进一步延长洪水预报的预见期,提高洪水预报的效益和作用[4]。降水量预报的精度成为洪水预报中影响有效预见期长短的关键因素[3],近年,水文集合预报技术、应用水文气象概率预报的发展增加了预报附加值,并能够延长预警提前时间[1],全球/区域数值天气预报模式已经可以给出相对比较准确的定量降水预报,但对于洪水预报定时、定点、定量降水预报的要求,降水预报的时段、雨带位置与量级的微量偏差都可能引起截然不同的洪水效应[3],中小河流由于流域面积小,地形地貌复杂,下垫面对降雨的形成影响较大,汛期局部性、单点性暴雨常引发洪水,数值天气预报模式更难以提供可靠的预报成果。枯季天气系统相对较为单一,受地形地貌影响小,数值天气预报模式预报成果准确程度较高。
开展枯水期径流过程的模拟对水资源配置、生态环境需水量的研究、抗旱救灾等十分重要,但一般情况下,仅利用降雨径流模型模拟出流域的日径流过程,对枯水期的径流过程很少给予关注,也很少对模拟结果的精度进行专门地评价,现有的研究往往将丰水期和枯水期作为一个整体进行考虑,先模拟出流域的整体日径流过程后,再对枯水径流进行分析[5],结合数值天气预报结果开展中小河流短期径流预报研究成果更为稀少。2006年,中国建立了T213全球中期集合预报系统和中尺度区域集合预报系统,预报时效达10~16 d[1],中央气象台对外公布未来7 d数值天气预报结果。本文以数值天气预报1~7 d降水量、推算的蒸发量预报结果及实时水文观测数据为资料,以中小河流枯季径流为分析对象,优选预报因子,基于二次回归正交旋转设计,研究枯季未来3、5、7 d枯季径流预报模型,探索气象水文耦合在中小河流枯季径流预报方法。
1 研究方法
影响径流量的因素中最主要的因素是降雨量、初始流域蓄水量和流域蒸发量[6],水文模型是根据已知的降雨时空分布、初始状态、模型的结构和参数等推求流域出口断面流量过程[7]。南方地区中小河流枯季径流以地下水补给为主,径流量大小主要取决于流域蓄水的多寡,枯季降水将增加流域蓄水,蒸发将消耗流域蓄水。据此,以数值天气预报中短期降水量、推算的蒸发量预报结果及水文观测数据为资料,基于二次回归正交旋转设计,构建短期径流预报模型,数据流程见图1。初始流域蓄水量通过流域前期实测河道径流量、降水量、蒸发量等因子集反映,预见期内降水量依据数值天气预报结果因子集反映,预见期内蒸发主要和天气状况相关,同天气状况下变化不大,可采用数值天气预报结果结合前期同天气状况下蒸发观测数据推算构建蒸发预报因子集。

图1 基于气象水文耦合的二次回归正交旋转设计短期径流预报模型数据流程Fig.1 Data flow design of short-term runoff forecasting model based on quadratic regression orthogonal rotation based on meteorological and hydrological coupling
二次回归正交旋转设计通过统计软件对试验结果进行非线性数学模型拟合,是一种将正交、回归、均有和较高饱和程度融为一体的试验设计方法[8],在正交设计的基础上,利用回归分析,在给出的因素和指标之间找出一个明确的函数表达式,建立因果关系的数学模型,以便定量地描述各因素对指标的作用,并用该数学模型预测[11],该方法在生物学研究中广泛应用[8-11],二次回归正交旋转设计径流预报模型数学表达式见式(1)。
(1)
式中:Qt为预报径流量,t=1,2,…,n;xi为优选的预报因子;m为预报因子个数;bi、bii、bij均为参数项;b0为常量。
模型拟定过程中,Qt使用实测值,xi可从流域前期实测河道径流量、降水量、蒸发量,预见期降水量、蒸发量通过因子分析法、经验法等优选确定,为已知值。因可能有多个xi形成多种组合通过相关性及显著性检验,各xi间可能存在多重线性关系,会给模型带来不合理的解释,致模型的稳定性差,造成预报模型可靠性差、精度低。为了得到一个可靠的预报模型,需要有效地从众多影响Qt的因素中挑选贡献最大的变量,建立最优的预报模型,这样的最优模型包含所有对Qt有显著影响的变量。在此推荐采用逐步回归分析法[14-16]推求式(1)最优预报模型结构、预报因子及参数值,该方法是从一个自变量开始,视自变量对Qt作用的显著程度,从大到小依次逐个引入模型,当引入的自变量由于后面变量的引入而变得不显著时,要将其剔除,引入一个自变量或从模型中剔除一个自变量,为逐步回归的一步,每一步都要进行F检验[11],以确保每次引入新的变量有统计意义。
本文使用DPS数据处理系统逐步回归分析法率定模型。限于篇幅,模型率定计算方法详见参考文献《DPS数据处理系统 第二卷 现代统计及数据挖掘》[11]关于逐步回归分析内容,在此不再复述。
2 实例应用
2.1 流域基本情况及资料
南汀河流域处于云贵高原西部边缘,横断山脉南延段,流域内姑老河水文站(东经99°14′、北纬23°41′)以上流域面积4 185 km2,海拔高差2 984 m,属中山地区典型的亚热带湿润立体气候类型,多年平均降水量1 600 mm,其中汛期(5-10)月份降水量约占全年降水量的90%,多年平均产水量56.8 亿m3,多年平均径流深701 mm。流域枯季径流以地下水补给为主,径流量大小取决于流域蓄水的多寡,同时,枯季降水将增加流域蓄水,蒸发将消耗流域蓄水,区域内水旱灾害频繁,通常是“三年一小旱,五年一大旱”。
本文选取南汀河姑老河水文站作为研究对象,资料包括姑老河水文站及上游6个雨量站1999-2003年、2006-2008年枯季日雨量资料、日蒸发资料及对应的实测日径流资料,均为云南省水文水资源局整编成果,资料来源可靠。1999-2008年10 a内,南汀河流域姑老河水文站以上无对径流产生较大影响的中大型水利水电工程建设,流域内土壤植被等产汇流条件未发生较为明显的变化,2002年以来,姑老河水文站降雨减少较为明显,但径流与降雨变化趋势一致[17],流域产汇流具有较好的一致性,本文选取1999-2003年、2006-2008年作为研究对象,资料可靠。
2.2 预报模型拟定
采用DPS数据处理系统软件提供的逐步回归分析法、收集到的1999-2003年枯季日雨量资料、日蒸发资料及对应的实测日径流资料分析确定最优预报模型结构、预报因子及参数值。姑老河站基于数值天气预报的未来3、5、7 d枯季径流预报模型结构、参数值、预报因子优选结果及模型见式(2)、式(3)、式(4)。

(2)
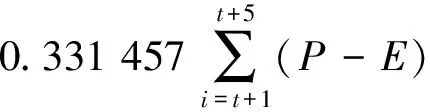
(3)

(4)

2.3 应用结果及分析
采用南汀河姑老河水文站及上游6个雨量站点1999-2003年枯季雨量资料、蒸发资料及相应实测径流资料依据预报模型进行拟合,2006-2008年枯季雨量资料、蒸发资料及相应实测径流资料对预报模型进行检验,结果见图2、图3、图4,由于篇幅限制,本文使用1999年11月-2000年4月、2007年11月-2008年4月未来3、5、7 d平均径流预报模拟结果与实际观测值比较作为示例说明拟合及检验情况。
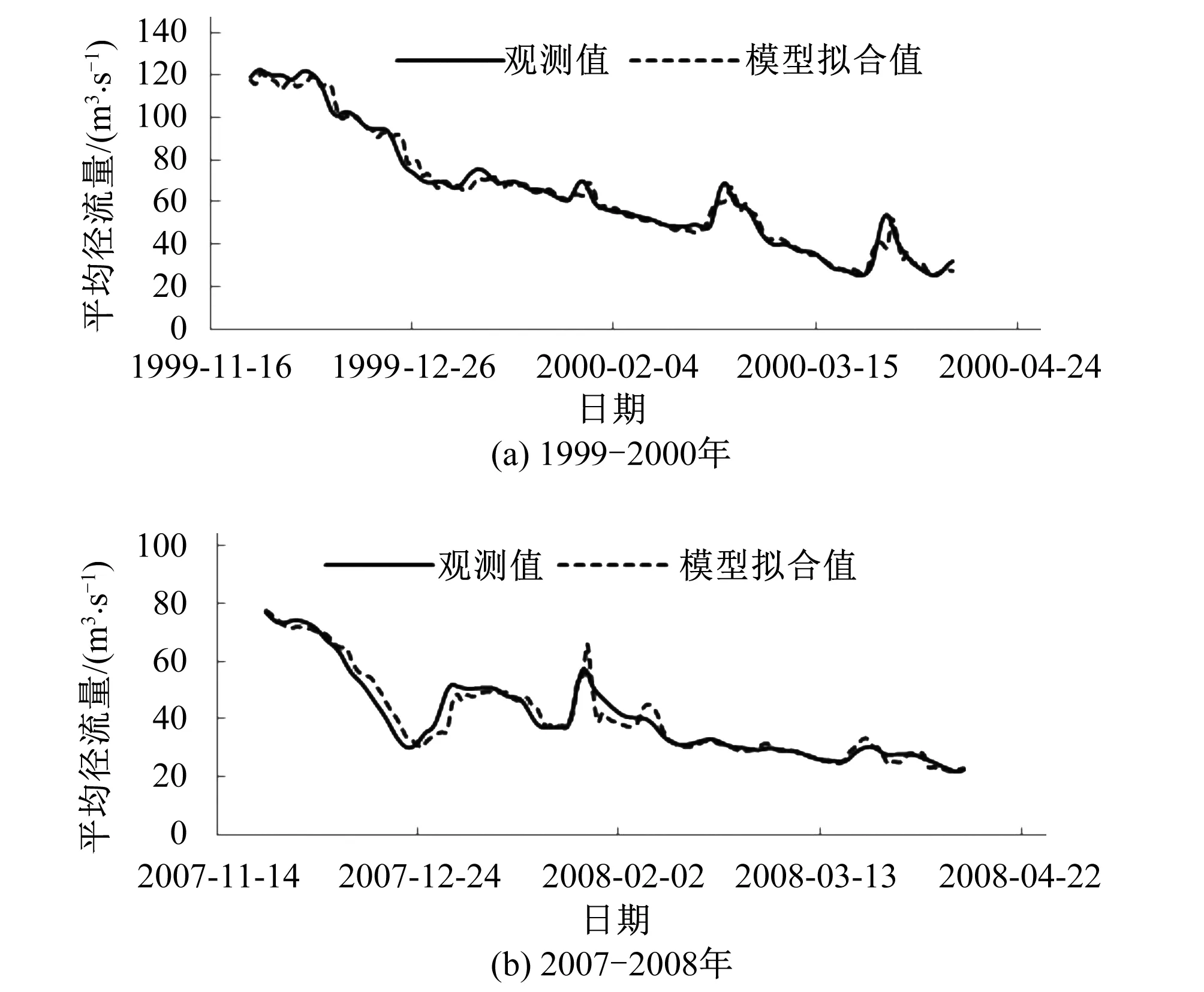
图2 姑老河水文站未来3 d径流模型拟合值与观测值比较Fig.2 Comparison of the fitted values and observations of the runoff model of the Gulaohe Hydrological station in the next 3 days

图3 姑老河水文站未来5 d径流模型拟合值与观测值比较Fig.3 Comparison of the fitted values and observations of the runoff model of the Gulaohe Hydrological station in the next 5 days

图4 姑老河水文站枯季未来7 d径流模型拟合值与观测值比较Fig.4 Comparison of the fitted values and observations of the runoff model of the Gulaohe Hydrological station in the next 7 days
根据《水文情报预报规范(GBT22482-2008)》,使用确定性系数、绝对误差、相对误差、合格率对姑老河站未来3、5、7 d径流预报结果进行分析。一次预报的误差小于许可误差时,为合格预报,径流预报许可误差取径流实测值的20%。
确定性系数:
(5)

绝对误差:
ΔQ=QC(i)-Q0(i)
(6)
相对误差:
δ=ΔQ/Q0(i)×100%
(7)
合格率:
(8)
式中:ΔQ为绝对误差;δ为相对误差;QR为合格率;n为合格预报次数;m为预报总次数。
表1为未来3 d径流模拟预报精度分析结果。由表1知,6个枯季模拟预报时段DC值最大为0.992、最小为0.948、平均为0.974,平均绝对误差最大值为2.59 m3/s、最小为1.32 m3/s、平均为1.96 m3/s,平均相对误差最大为5.6%、最小为2.9%、平均为4.2%。预报合格率最大为99.3%、最小为97.9%、平均为98.8%,达到甲级精度等级。
表2为未来5 d径流模拟预报精度分析结果。由表2知,6个枯季模拟预报时段DC值最大为0.989、最小为0.909、平均为0.960,平均绝对误差最大值为3.10 m3/s、最小为1.49 m3/s、平均为2.36 m3/s,平均相对误差最大为7.4%、最小为3.2%、平均为5.1%。预报合格率最大为100%、最小为92.0%、平均为97.8%,达到甲级精度等级。
表3为未来7 d径流模拟预报精度分析结果。由表3知,6个枯季模拟预报时段DC值最大为0.988、最小为0.865、平均为0.947,平均绝对误差最大值为3.53 m3/s、最小为1.56 m3/s、平均为2.61 m3/s,平均相对误差最大为8.8%、最小为3.3%、平均为5.7%。预报合格率最大为100%、最小为89.7%、平均为97.5%,达到甲级精度等级。
由表1至表3,随着预见期延长,预报精度有所下降,但下降不明显,均满足甲级预报精度要求,可用于对外发布正式预报。

表1 姑老河水文站枯季未来3天径流预报结果分析Tab.1 Analysis of the runoff forecast results of the Gulaohe Hydrological station in the next 3 days
3 结 语
(1)本文以数值天气预报及前期实测河道径流量、降水量、蒸发量为输入,优选预报因子,基于二次回归正交旋转设计,建立了中小河流枯季径流预报模型,探索了基于水文气象耦合中小河流枯季短期径流预报方法,经在南汀河姑老河水文站未来3、5、7 d枯季径流模拟中应用,效果理想,精度较高,虽然随着预见期延长,模型预报精度有所下降,但下降不明显。
(2)本文使用的短期径流预报方法选用的预报因子为预报模型提供了良好的物理基础,同时降低了模型结构的复杂程度及计算量,在取得良好的预报精度同时,预见期由基于实测降雨的15 h左右分别延长至3、5、7 d,可满足枯季水资源科学调度、抗旱救灾、水生态保护决策重点关注的不同预见期短期径流预报的需要,且该方法操作简单,易于实现,具有较好的推广价值。
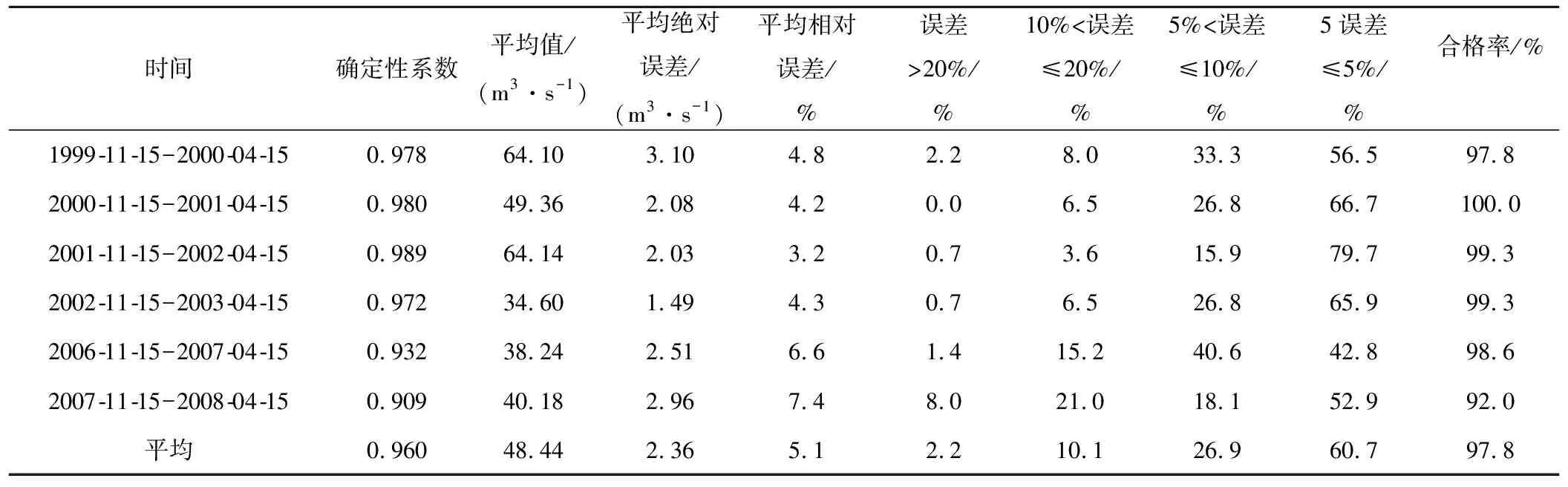
表2 姑老河水文站枯季未来5天径流预报结果分析Tab.2 Analysis of the runoff forecast results of the Gulaohe Hydrological station in the next 5 days
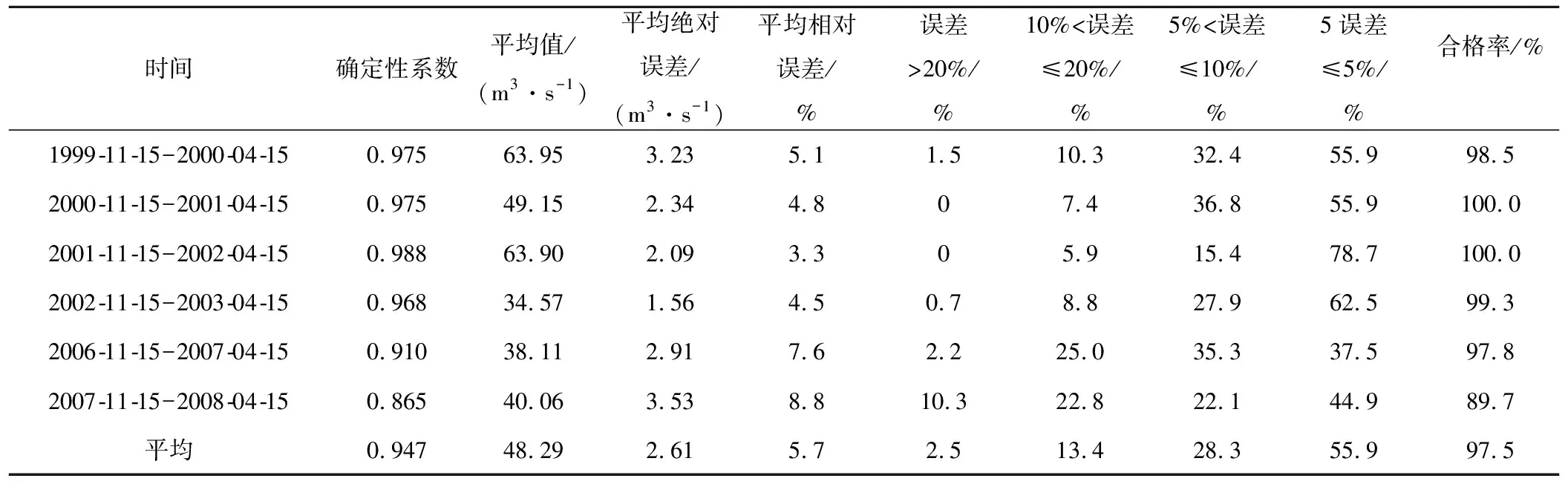
表3 姑老河水文站枯季未来7天径流预报结果分析Tab.3 Analysis of the runoff forecast results of the Gulaohe Hydrological station in the next 7 days
(3)汛期数值天气预报模式预报成果因无法满足中小河流洪水预报对定时、定点、定量降水预报的要求,一直以来主要用于洪水参考性估报,枯季由于洪水灾害较少,关注度较低,需求稍显不足,同样相关研究成果较少。本文考虑到枯季数值天气预报模式预报成果精度相对较高,枯季对短期径流预报的需求大于洪水预报的实际情况,探索了中小河流气象水文耦合短期径流预报的方法,通过南汀河姑老河水文站实例应用显示,气象水文耦合在中小河流枯季径流预报中,可取得良好的预报精度,应用前景较为广阔。
(4)本模型适用于汛期降水集中、占比大,枯季降水稀少、天气系统相对较为单一的季风气候区的枯季径流预报。由于本文使用了一个代表流域作为分析对象,且用于模型建立及检验的资料较少,还有待进一步深化研究。
□
