设备振动传递路径的频响函数计算方法研究
2018-11-28张小磊石学涛姚抒均
王 楷, 郑 凯, 张小磊, 石学涛, 姚抒均
(齐鲁工业大学(山东省科学院) 山东省科学院海洋仪器仪表研究所, 山东 青岛 266000)
引言
随着振动源分离技术的发展,传递路径分析(TPA)法[1]被引入到船舶领域。传递路径分析法可以准确分析系统中各台设备的贡献量,确定主要振源,从而针对主要振源,有的放矢的提出改进设计。但是,由于传递路径分析需要测量大量的频响函数,测试工作量大且测试不便,限制了传递路径分析法的应用范围。近年来,国内外学者为解决这一问题进行了很多探索和研究,其中工况传递路径分析(OPA)法[2]得到了很大重视。工况传递路径分析不需要测量频响函数,仅需要获得系统在工作状态下评估点和激励点的响应即可进行分析。Gert De Sitter和ChristofDevriendt[3]等人提出一种不用拆解系统即可识别传递路径的方法。该方法首先运用在简单离散系统上,通过整理得到关于传递函数的表达式,然后运用H1估计得到传递函数的计算式。但是在实际应用中,结构的传递函数表达式很难获得,且各个激励力不相关的条件难以满足,以至于限制该方法的应用。K.Janssens和A.Ossipov[4-5]等人介绍了一种运用传递率理论的OPA方法。文中指出尽管该方法可以减少测量时间,减轻测量的复杂程度,但是也存在很多限制:首先,输入载荷应是不相关的;其次,结构输入路径之间不应存在互耦合;最后,在测量中可能遗漏重要路径。
1 基本原理
工况传递路径分析法是在传递路径分析法[6]的基础上发展演变而来的,其基本原理基于假设:来自不同路径的所有部分响应构成了总响应。

式中:Xj为评估点j处的总响应,Xij为传递路径ij在评估点j处的响应分量。
响应分量Xij是激励点处的激励力通过频响函数在评估点处引起的响应,其表达式为:

式中:Hij为激励点i到评估点j的频响函数,Fi为作用于激励点i处的激励力。
在传递路径分析法中,频响函数Hij是通过锤击实验[7]获得的,但是在工况传递路径分析法中,频响函数是通过计算得到的。因此,频响函数Hij的计算方法即为工况传递路径分析法的关键技术。
为计算频响函数,本文提出三种方法:多工况法、分段函数法和多工况分段函数法。下面分别予以说明。
1.1 多工况法
利用多工况法计算频响函数,振动系统需要具有足够多的不同工况。对于具有一台或多台设备的振动系统,可以通过改变设备的工作状态或者开关某台设备,以获得不同的工况。假设系统有m个频响函数,k个工况。根据式(1),每个工况列一个方程,其公式如下:

式中:下标m为频响函数编号,下标k为工况编号,下标j为评估点编号。
当工况数目k大于或等于频响函数数目m时,即可求得m个激励点到评估点j的频响函数:

式中:[H]为频响函数矩阵,[X]为评估点响应矩阵,[F]为激励力矩阵,[F]+为[F]的广义逆。
1.2 分段函数法
利用分段函数法[8]计算频响函数,首先假设频响函数在某频段内为一个可以用参数a1,a2,…,an表示的函数:
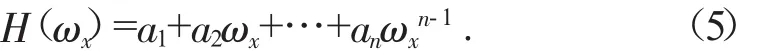
式中:下标n表示参数的编号。
利用在这个频段内多个采样频率点ωx测量得到的响应值Xj(ωx)与激励力的值F(ωx),列出足够多的方程,求解频响函数中的参数 a1,a2,…,an。
假设系统有m个频响函数,每个频响函数在[ω1,ω2]频段内可以表示为含有n个参数的函数H(ωx),则在[ω1,ω2]频段内至少需要 m·n 个采样频率点,才能求得频响函数中的m·n个参数。根据式(1),在每个采样频率点ωx处列一个方程,如式(6)所示:
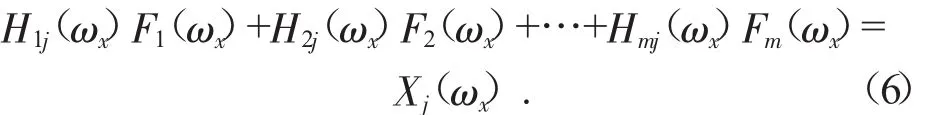
式中:ωx∈(ω1,ω2),下标 m 为频响函数编号,下标 j为评估点编号。
如果在分析频段内,频响函数分为s段,则其表达式为:
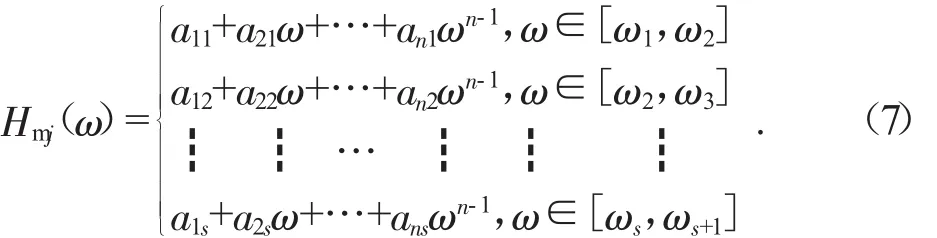
式中:下标m为频响函数编号,下标j为评估点编号,下标s为频响函数分段编号,下标n为频响函数参数编号。
1.3 多工况分段函数法
在工程实际中,振动系统的可变工况数目不多,从而限制了多工况法的运用;对于分段函数法,每个频段内采样频率点的数目不能过多,否则会因各采样频率点间的差异过小而产生奇异矩阵,导致求解错误。鉴于以上两种方法的缺陷和不足,工程实际中两种方法可以结合使用,增加可用方程的数目,以便提高计算精度。
假设振动系统有k个工况,m个频响函数,每个频响函数在[ω1,ω2]频段内可以表示为含有n个参数的函数,则在[ω1,ω2]频段内仅需要 m·n/k 个采样频率点,就能求得频响函数中的m·n个参数。为了提高计算精度,需要增加方程的数目。因此采样频率点个数应大于m·n/k。根据式(1),每个工况列一个方程,则在每个采样频率点ωx处可列一个含有k个方程的方程组,如式(8)所示:

式中:ωx∈(ω1,ω2),下标为 m 频响函数编号,下标 k为工况编号,下标j为评估点编号。
由式(8)计算得到各参数后,即可按照式(7)获得各频响函数的表达式。
2 实验与结果分析
2.1 实验步骤
为了检验通过多工况分段函数法计算得到的频响函数的准确性,在实验室内选用一台海水泵进行实验研究。海水泵附有进口管路和出口管路,其安装如图1所示。海水泵四个机脚通过隔振器与基座相连,进口管路、出口管路通过隔振器与马脚相连。
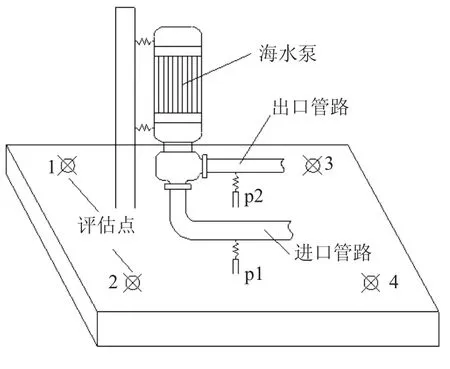
图1 海水泵安装示意图
实验中,每个机脚考虑3个方向激励,布置三向加速度传感器。每个管路马脚只考虑1个方向激励,布置单向加速度传感器。评估点选在距设备与管路激励点距离相当的基座上,共计4个,布置单向加速度传感器。因此,该振动系统中,每个评估点对应14条路径,即14个频响函数。
海水泵与管路安装前,通过锤击实验获得各路径的频响函数,以便与计算得到的频响函数进行对比。实验时,根据互易原理[9],装有力传感器的力锤在靠近评估点的位置激励,加速度传感器安放在激励点处采集响应信号。通常一个位置敲5~10次,最后的结果取平均值。本次锤击实验中,力锤锤头使用的是钢头。一般而言,在中高频段内采用钢头进行锤击可以获得较好的频响函数。因此,本次实验的分析频段选为 300~700 Hz。
海水泵与管路安装后,开启设备。待设备运转稳定后,采集各激励点与评估点的响应信号,作为工况一。停止采集后,调节进出口管路压力,待设备再次稳定后,采集响应信号,作为工况二。
2.2 数据处理及结果分析
本实验中,各激励点处的激励力是基于隔振器阻抗特性[10]计算得到的。由于本实验中的频响函数数目较多,且系统可变工况较少,不能准确计算出全部频响函数。在不失一般性的前提下,本实验仅对管路的频响函数进行计算和验证。因此,将锤击实验中得到的设备机脚对应的频响函数作为已知量,代入式(9)中。将进口管路和出口管路对应的频响函数作为未知量,运用第2节中的三种方法分别进行求解,并与锤击实验得到的频响函数进行比较,其结果如图2所示。
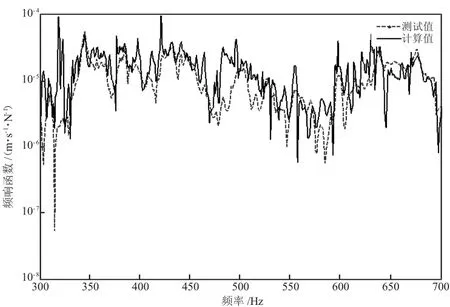
图2 多工况法的计算结果
由图2可知,两曲线在分析频段内趋势一致,但部分频率处,方程组的奇异性严重,计算值曲线的峰值过大,导致总级误差偏大,结果不可取。由图3可知,两曲线在分析频段内量级一致,但趋势吻合较差,结果亦不可取。由图4可知,两曲线在分析频段内趋势和峰值均吻合较好。在个别频率处,计算值曲线的峰值偏大,这是由于在该频率处方程组的奇异性无法消除,导致误差被放大。经计算,多工况分段函数法的计算值与锤击实验的测试值在分析频段内的总级相差1 dB,满足工程要求。这表明:由多工况分段函数法计算得到的频响函数具有较高的准确度,运用该方法计算振动系统的频响函数是切实可行的。
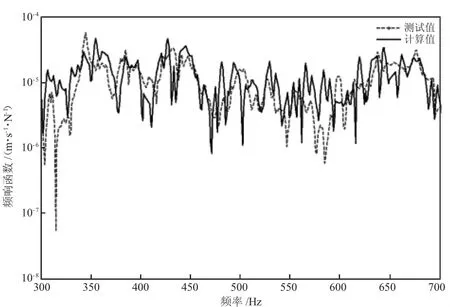
图3 分段函数法的计算结果
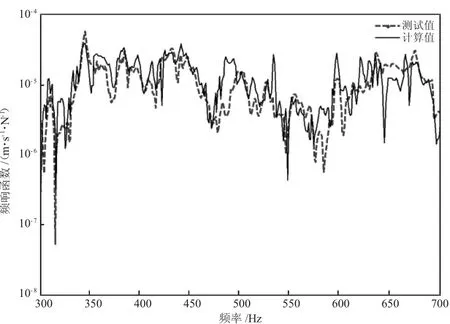
图4 多工况分段函数法的计算结果
3 结论
运用多工况分段函数法计算得到的频响函数与锤击实验得到的频响函数,在分析频段内吻合较好,两者总级仅相差1 dB,满足工程要求。由此可知,多工况分段函数法计算的频响函数具有较高的精度。
在振动系统具有足够多可变工况的情况下,完全可以运用该方法计算所有的频响函数,避免测量频响函数,实现该系统的工况传递路径分析。多工况分段函数法为工况传递路径分析提供了重要技术支撑,为工况传递路径分析的推广应用奠定了理论基础。
