沈阳市PM2.5浓度ARIMA-SVM组合预测研究

宋国君,国潇丹*,杨 啸,刘 帅



沈阳市PM2.5浓度ARIMA-SVM组合预测研究

宋国君1,国潇丹1*,杨 啸1,刘 帅2

(1.中国人民大学环境学院,北京 100872；2.农业农村部管理干部学院,北京 102208)

首先利用回归树分类方法,对采暖期与非采暖期各日进行气象类型划分,识别出易造成重污染天气的气象类型.其次分别在各气象类型内,以污染源排放量为自变量,利用差分自回归滑动平均与支持向量机(ARIMA+SVM)组合方法建立起PM2.5浓度日均值预测模型,并选取2013年01月~2017年06月间,沈阳市区内9个环境监测点PM2.5浓度日均值进行实证分析.结果表明,使用气象分类下的ARIMA+SVM组合模型对PM2.5浓度日均值进行预测,相比于不划分气象类型时的普通机器学习模型,其模型预测值与实测值趋势的吻合度更高,且对峰-谷值的识别能力更强.在采暖期与非采暖期,组合模型均具有平均绝对误差更低、预测正确率更高的优点.

PM2.5浓度；气象类型；ARIMA-SVM组合模型；预测方法

随着我国经济发展进入新常态,空气质量已成为最受关注的民生问题之一.作为影响我国空气质量的首要污染物,PM2.浓度的准确预报对预判重污染天气,制定应急预案启动机制,优化企业限产方案具有重要意义.

美国、澳大利亚等国家早在20世纪就开展了大规模的城市空气质量预报研究[1].我国自2001年起开始发布空气质量预报,预报模型包括机理模型和非机理模型[2].机理模型以实时探空气象内插和污染监测资料构建初始场,并加入地面气象和污染源排放资料,经过复杂的网络嵌套和推演过程,得出未来24~48h的污染物浓度预报值[3],主要包括中国科学院大气物理所开发的“城市空气污染预报(EMH)”、中国气象局气象科学研究院开发的“城市空气污染预报(CAPPS)”和“雾-霾数值预报(CUACE/Haze-fog)”三个模型[4].模型涵盖了污染物由产生到扩散的复杂物理化学过程,但其初始场构建十分困难,预报过程复杂,对于未使用过相应系统和大气物理知识缺乏的普通研究者来说,几乎无法操作和复制.

非机理模型则通过历史数据来判断污染物浓度变化规律,主要包括统计模型和机器学习模型[5].目前已有很多学者选取污染物浓度、温度、湿度、气压、风速、水汽压等影响因子,使用多元线性回归、小波神经网络、支持向量机模型对PM2.5等浓度进行预测[6-10].非机理模型未将污染物的形成过程同气象条件影响下的污染物扩散过程分离开,不符合科学机理,且未将可控的生产行为与不可控的天气现象区别开.另外,以污染物浓度作为预测自变量的方式,认为PM2.5浓度与SO2、NO等污染物具有直接关联,忽略了由工业生产、燃料燃烧、交通运输、扬尘等形成的PM2.5一次来源,未关注造成大气污染的人类行为本质,对污染源管理并无借鉴意义.在进行预报时,除需要输入常规气象要素预测值外,还需要输入其他污染物浓度预测值,对预测精度产生了很大影响[3].

强逆温、高湿度、偏南风、低气压天气对沈阳市空气污染扩散明显不利[11].为避免客观条件制约对主观管理效果的弱化,应将气象因素与污染物来源分开.本文综合机理与非机理模型提出一种全新的城市PM2.5浓度预测方式.首先,使用回归树方法,对沈阳市每个自然日进行气象类型划分,使得类型内部各天的扩散模式近似相同.随后,在每个类型中以污染源日排放量为自变量,使用“差分自回归滑动平均-支持向量机(ARIMA-SVM)”组合模型进行PM2.5浓度预测.ARIMA-SVM组合预测方法既拟合了历史数据的线性关系,又对残差部分进行了非线性建模,避免了普通SVM预测模型对具有明显下降趋势的时间序列进行预测时,结果偏高的问题;模型相比于常规SVM及已有文献中使用距离相关系数等优化后的SVM模型,均方根误差可降低2.42%~33.93%[12-13].本文所提出的优先进行气象分类的思想,不仅可以识别出易引起PM2.5浓度超标的类型,也便于对恶劣扩散天气设计有针对性的应急响应措施.未来可通过修改污染源排放量的方式,判断各点源减排贡献率和成本有效性,为空气质量达标规划的设计提供可靠依据.

1 研究方法

1.1 研究思路

图1 研究思路逻辑框

本文提出了一种全新的城市PM2.5日均浓度预测方法,这种方法首先基于回归树分类法对各日进行气象要素组合分类,使得各类型中气象条件基本相同,将不受控的客观因素与可控的污染源排放分离开,突出空气质量管理绩效;随后在各气象类型内分别进行ARIMA+SVM组合预测,使用历史数据进行机器学习,识别PM2.5浓度与污染源排放量间的关系;在实际预测中,使用气象预报数据判断目标日气象类型,并将该日污染源排放量预测值带入所属类型ARIMA+SVM模型,得出PM2.5浓度预测值.整体研究思路如图1所示.

1.2 回归树气象分类方法

污染物的扩散、稀释、积聚和滞留都受到气象条件的影响[14-15].PM2.5浓度与湿度、风速、风向、气压、气温等具有密切关联[16-17].对于北方采暖城市,冬季采暖期PM2.5浓度明显高于其他季节[19].不同季节PM2.5浓度的气象影响因素也有所不同,夏秋季主要为气压与风速[19],春冬季主要为相对湿度和日照时数[20].降雨对颗粒物具有清洗作用,通过稀释和沉降引起PM2.5浓度降低[10].相对湿度对PM2.5浓度影响显著,当湿度较大时形成雾,引起颗粒物变重下沉,同时阻碍烟气扩散,加重污染[10].风向也是重要的影响因素,城市上风向无大量污染源、风速超过一定数值时有利于污染物扩散[21].出现逆温现象时PM2.5浓度升高,逆温层随着气温升高而消失[22].气压高时污染物随着气流向城市周边地区扩散[23].但温度高时,空气受热膨胀又形成低气压,使气压与PM2.5浓度的关系变得复杂.

使用已知的影响PM2.5浓度的气象要素,对各个自然日进行气象类型划分,可判断空气污染超标发生的气象规律,识别造成沈阳市重污染天气的气象成因,同时使得各类型内部的气象影响基本被剔除,突出了管理手段对PM2.5浓度的影响.已有学者使用聚类分析等方法进行气象分类,而这种非监督分类方式需要人为确定最优分类数量,且不适合将PM2.5浓度作为分类目标[24].本文所使用的回归树分类方法可通过对自然日的不断分类,使得每一类气象内部的PM2.5浓度相似性最大化,同时与其他类型之间的差异性最大化[25].回归树分类法的优点在于:首先,以PM2.5浓度作为气象特征值分割对象,考虑了污染物与气象条件之间的影响关系;其次,可以给出唯一最优的分类数量和结果;另外,其相比于各种深度学习方法,具有更强的可解释性.

回归树分类的步骤包括:(1)树根节点聚合全部样本;(2)遍历每一个气象特征的特征值,每个特征值得到一个划分,通过比较找出使得各叶节点内部纯度最高的最优划分结果;(3)持续寻找气象特征进行划分,直到各节点内样本不纯度降低至预先设定的阈值[26].对于目标变量是连续变量的回归树来说,使用最小平方残差SS来度量树的不纯度,计算公式为:

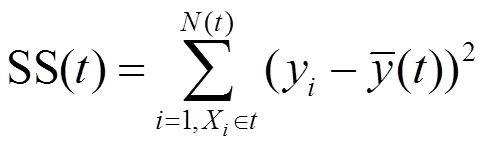
式中:为节点内样本,()为节点内样本总量,X为样本点,y为样本值.

1.3 ARIMA+SVM组合预测方法

据中国空气质量检测平台中数据显示:沈阳市2013~2017年PM2.5浓度时间序列出现明显下降.差分自回归滑动平均(ARIMA)模型基于线性方法进行定阶,可以很好地拟合出时间序列的线性趋势.但另一方面,PM2.5浓度经常出现复杂噪声,导致ARIMA模型无法捕捉这部分非线性规律,导致预测精度不高[27].而支持向量机(SVM)在处理小样本、非线性时具有明显优势,可规避其他机器学习算法中易于出现的局部极小以及过拟合现象,已被广泛应用于空气质量预测领域[6,28].由于沈阳市PM2.5浓度时间序列同时具有明显的线性和非线性特点,本文将使用已在股票价格、发病率、用户数量预测领域具有广泛应用的ARIMA-SVM组合模型对其进行预测[29-31].首先使用ARIMA模型描述历史的线性关系,随后使用SVM模型对ARIMA模型无法捕捉的残差部分进行非线性建模.

图2 ARIMA-SVM组合预测流程图

ARIMA-SVM组合预测流程如图2所示,具体步骤包括:

(1)ARIMA模型预测.ARIMA(p,d,q)模型是针对非平稳时间序列所建立的模型,非平稳经d阶差分后得到平稳序列,建立ARIMA(p,q)模型,模型的一般形式为:

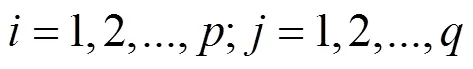
式中:y为平稳时间序列;为白噪声序列.通过绘制自相关图与偏相关图,可确定模型自回归阶数p和移动平均阶数q.定阶后可得到模型拟合参数、.

综上,最终的最优判别函数满足等式(5).

2 预测结果

2.1 数据来源与处理

沈阳地区PM2.5浓度数据来源于中国空气质量监测平台,污染源排放数据来源于沈阳市污染源在线监控系统,气象数据来自于中国气象局中国地面国际交换站气候资料日值数据集(V3.0).本文中全部采用日均数据,时间为2013年01月~2017年06月.

气象数据中:气压、气温、相对湿度、风速、地表气温指标采用数据集中沈阳市地面区站(编号54342)日均值,降水量采用日累计降水量,蒸发量采用小型蒸发量,风向采用16方位制日极大风向,由正北方起顺时针编号.

沈阳市作为典型的北方采暖城市,一年中有5个月的采暖期(11月~次年3月)和7个月的非采暖期(4~10月),大量的供暖锅炉和热电厂仅在采暖期运行.采暖期与非采暖期在气象条件和污染来源方面均有明显不同,为提高模型预测精度,需要在预测之初就将二者分开,分别进行气象分类及后续预测.

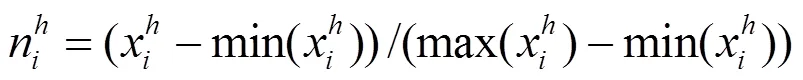
2.2 气象分类结果

由Pearson相关分析结果可知:沈阳市采暖期整体PM2.5浓度与相对湿度呈高度正相关,与日照量、风向、蒸发量呈高度负相关;而蒸发量与高低气温、蒸发量呈高度正相关,与气压、相对湿度呈高度负相关;日照量又与降水量、最低温度、相对湿度呈高度负相关.在非采暖期,沈阳市PM2.5浓度与气压呈高度正相关,与高低气温、蒸发量呈高度负相关,各气象因子之间也存在与采暖期类似的相关关系.将所获取的全部气象要素作为自变量,以沈阳市PM2.5浓度为因变量,使用回归树的方法,对2013年01月~2017年06月全部自然日进行气象类型划分.R软件输出的气象分类结果如图3所示.R软件同时给出回归树模型的标准化均方误差,采暖期为6.130´10-33,非采暖期为4.499´10-34,说明回归树分类结果合理可靠.

在上述气象要素中,地温、平均温度、日照量、蒸发量属于气象预报无法进行或不给出的指标.为了进行后续污染物浓度预测,需要对气象分类结果进行调整.对于采暖期,回归树中后四枝由蒸发量进行区分,由于该指标无法预测,且四枝中所包含样本量占比仅为11%,均为高浓度天气,因此将其合并为一类.类似地,将非采暖期后三枝合并.气象预报中可以给出是否降水的判断,但无法预测降水量,因此将采暖期中第三步降水量³0.45mm以及非采暖期中第四步降水量³0.15mm的判定条件均改为>0mm.原始的降水量判别条件数值不大,调整后仅有8个采暖日(1.15%)和4个非采暖日(0.42%)的气象类别有所调整,调整前后的差异可以忽略.最终得到如表1所示的沈阳市气象分类结果.

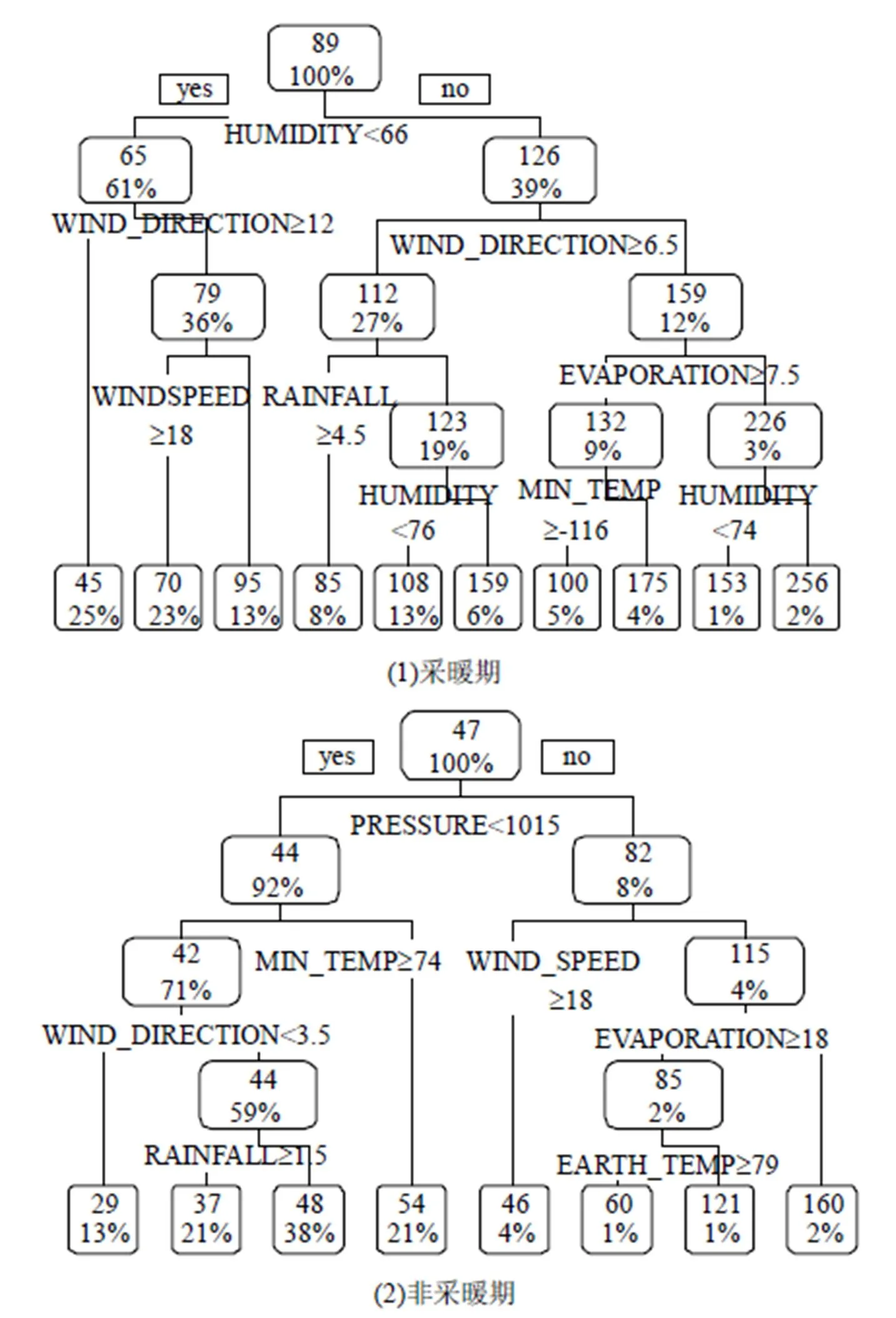
图3 沈阳市气象分类回归树

PRESSURE-气压(0.1hPa)、RAINFALL-降水量(0.1mm)、MAX_ TEMP-最高气温(0.1℃)、MIN_TEMP-最低气温(0.1℃)、WIND_ SPEED-风速(0.1m/s)、WIND_DIRECTION-风向(16风向)、 HUMIDITY-相对湿度(%)、EARTH_TEMP-地温(0.1℃)、 AVERAGE_TEMP-平均温度(0.1℃)、SUNLIGHT- 日照量(0.1h)、EVAPORATION-蒸发量(0.1mm)

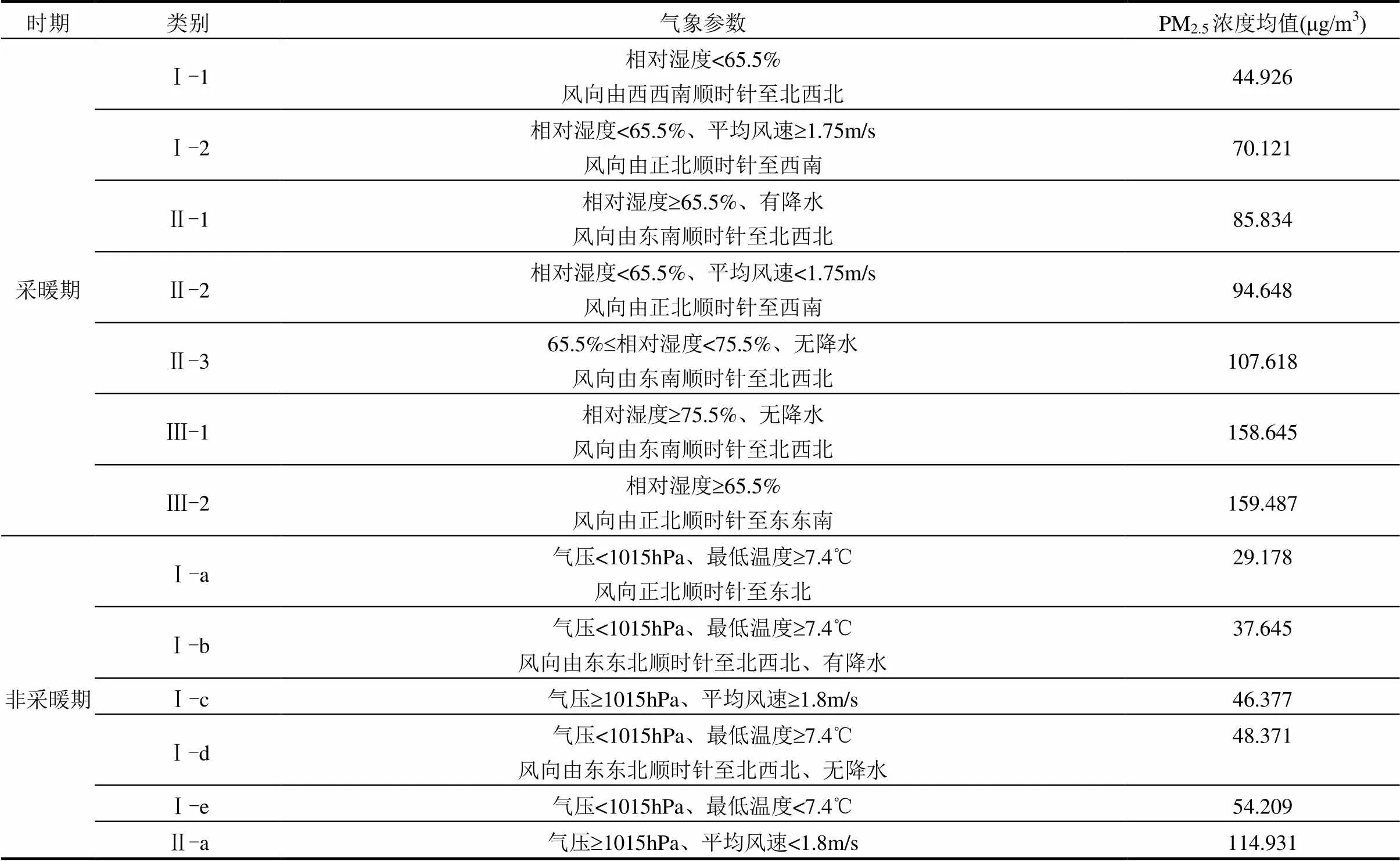
表1 沈阳市自然日气象分类结果

为突出易造成重污染的气象,本文依据国家24h平均浓度二级标准将气象类别分为3类,其中Ⅰ类为PM2.5浓度均值为不超标类型(浓度<75μg/m3),Ⅱ类为超标类型(75μg/m3£浓度<150μg/m3),Ⅲ类为严重超标类型(浓度³150μg/m3).在各类别内部按平均浓度由小到大进一步排序.

2.3 模型预测结果

2013年01月~2017年06月沈阳市共有9个具有连续监测数据的国控大气监测点.如表2所示的描述统计结果可知:各站点PM2.5浓度的极值跨度很大,均值均未超标,变异系数接近1,说明浓度值变异程度高,预测难度大.

使用SPSS19.0软件进行ARIMA时间序列预测,对PM2.5浓度序列中的线性部分进行识别.首先,通过时间序列ADF单位根检验可知,各监测点均拒绝原假设,不存在单位根,属于平稳时间序列.ARIMA (p,d,q)模型转化为不存在季节趋势的ARMA(p,q)模型.随后,通过自相关与偏自相关系数图识别模型参数p和q.以采暖期小河沿为例,如图4所示的ACF图出现明显拖尾性,而PACF图自=1后截尾,无明显模式,说明采暖期小河沿监测点满足平稳的AR(1)模型.类似地可知:采暖期全部监测点满足AR(1)模型,非采暖期全部监测点满足AR(3)模型.

表2 2013年01月~2017年06月沈阳市各监测点PM2.5浓度描述统计结果

注:2015年04月沈阳市对市内国控监测点名称进行更改,括号内为更名前名称.

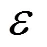
图4 采暖期小河沿监测点自相关系数与偏自相关系数

分别在采暖期和非采暖期,以9个监测点PM2.5浓度的ARIMA预测残差为因变量,以沈阳市全部污染源排放量为自变量,使用MATLAB软件,选取2016年12月(采暖期)及2017年06月(非采暖期)为测试集,其余月份为训练集,进行SVM预测.受数据可得性的限制,本文目前仅以安装在线检测系统的固定源排放量为模型自变量,未来可通过获取无在线监测固定源的环统数据、道路车流量数据、面源排放量数据,进一步提高模型的全面性及预测精度.沈阳市现有161个安装烟气在线监测系统的国控固定源,其中采暖期有132个固定源的数据质量满足需求,非采暖期有101个.以上述固定源排放量带入SVM预测,识别出PM2.5浓度的非线性变化部分,确定浓度与污染源管理水平之间的关系,未来可通过改变自变量输入判断各污染源减排量对PM2.5浓度变化的贡献.

表3 ARIMA回归方程参数

Table 3 ARIMA regression equation parameters

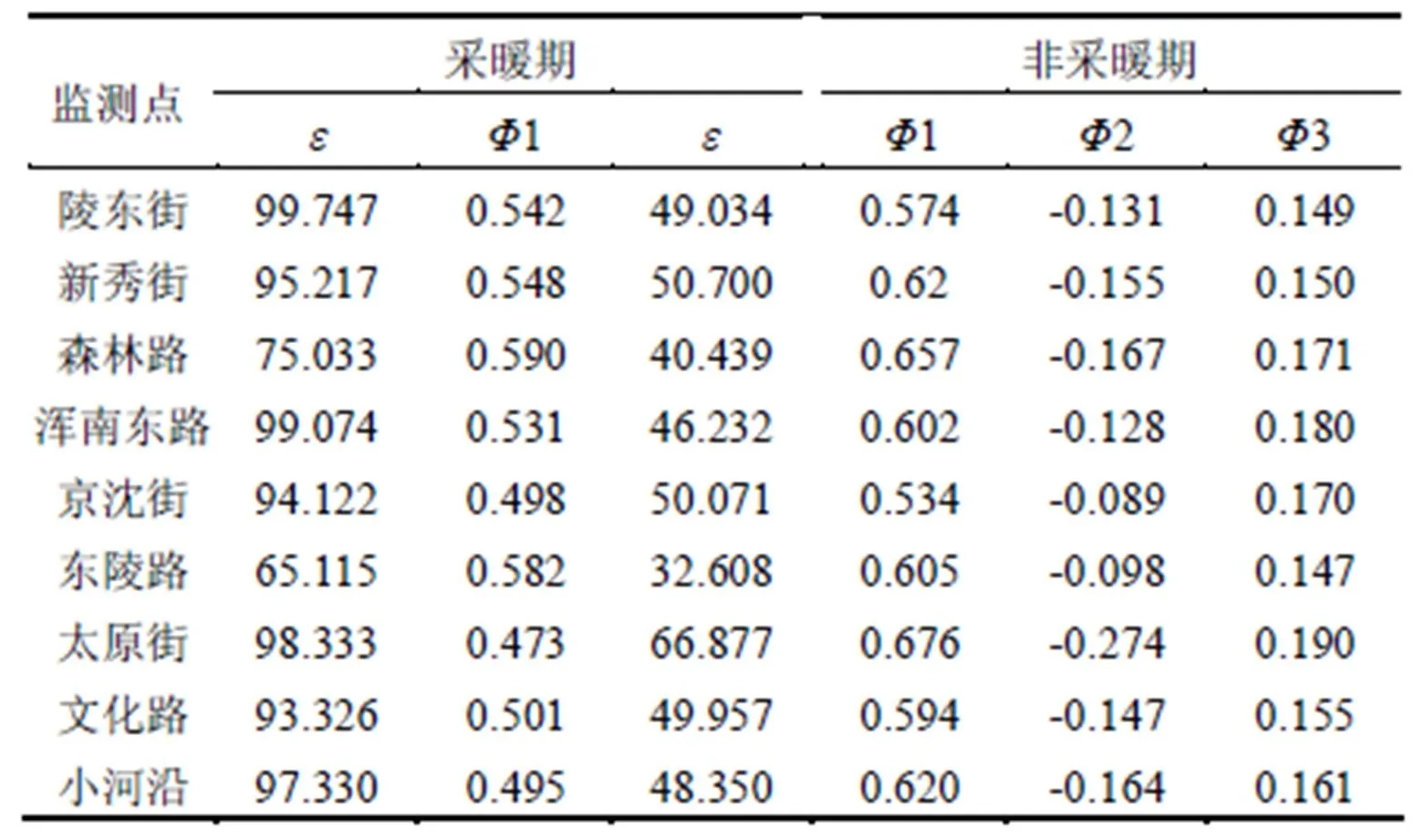
将残差部分的SVM模型预测值与ARIMA模型预测值加总,获得最终的PM2.5浓度预测值.因受篇幅限制,本文仅给出如图5~图6所示的小河沿监测点测试集预测值对比图.

图5 2016年12月小河沿监测点PM2.5浓度预测值对比

Fig.5 Comparison of predicted PM2.5concentration in Xiaoheyan monitoring site in December 2016

由多种方法预测结果对比图可知:(1)不划分气象类型时的预测值平缓,与实际值变化趋势整体吻合,但无法识别由恶劣气象条件导致的短期峰-谷值;(2)聚类气象分类下的预测结果不符合实际值变动趋势,多出现异动;(3)回归树气象分类SVM模型由于未使用时间序列模型拟合下降趋势,导致预测值平均偏高幅度超10μg/m3,部分采暖期单日被高估49μg/m3,非采暖期中58%的优等级测试日被错判为良等级;(4)回归树气象分类ARIMA+ SVM组合预测结果更接近实际值,对峰-谷值的识别能力明显提高,尤其在受关注的重污染天气预测效果更好.

图6 2017年6月小河沿监测点PM2.5浓度预测值对比

3 预测效果评价

为进一步证明使用回归树气象分类下的ARIMA+SVM组合模型预测沈阳市PM2.5浓度的合理性,评价模型预测效果,本文使用均方根误差(RMSE)、平均绝对误差(MAPE)、与实际值相关系数(r)3项指标,对不分气象类型的SVM预测、聚类分析气象分类SVM预测、回归树气象分类SVM预测、回归树气象分类ARIMA+SVM预测4个模型进行精度评价及对比.上述评价指标分别满足等式(8~10).除上述统计学指标外,本文也使用广泛应用于空气质量预报实际工作中的指数分级法判断预报正确率()[3].

由如表4所示的预测精度对比情况可知:采暖期中,回归树气象分类下的ARIMA+SVM组合预测模型的均方根误差均值最低,相关系数达到0.731,说明预测值与实际值显著相关,正确率均值明显高于其他模型;而且组合模型对太原街、文化路等城中心区域监测点的预测效果更好.非采暖期中,组合模型的均方根误差最低,平均绝对误差仅为0.412,预测正确率更高,相关系数略低于不分气象类型预测方法.

沈阳市现有的空气质量数值预报模型,在非采暖期的未修正预报正确率不足5%,使用污染物浓度观测值进行人工修正后正确率可达到约60%[32].本文所构建的ARIMA+SVM组合预测模型,无人工修正过程,采暖期综合正确率为51.20%,预报等级偏差超过一级的日数仅占3.20%;非采暖期综合正确率达到61.20%,不存在预报等级偏差超过一级的情况.综上所述,回归树气象分类下的ARIMA+SVM模型预测效果明显优于其他方法.

目前,本文所构建的组合模型已实现为在线空气质量预测预警系统,并实际应用于本溪、咸阳等城市,均取得了良好的预测效果.但由于受到数据可得性的限制,未能使用小时尺度数据对模型精度做进一步提升,导致在气候及浓度波动显著的自然日中,使用日均值数据得到的预测结果可能偏离实际值,且无法反映1h浓度波动趋势.另外,使用沈阳市地面站气象数据进行全市9个监测点的浓度预测,忽略了监测点间气象要素的差异,可能使预测结果存在一定偏差.未来在获取相应数据后,可对结果进行优化.

表4 模型预测精度对比

4 结论

4.1 构建回归树气象分类下的ARIMA+SVM组合模型,对PM2.5浓度日均值进行预测,预判重污染日期.在预测之前依据影响污染物扩散的气象条件,对各日进行气象分类,将主-客观因素分开,以核定空气质量管理工作的绩效水平,计算污染源减排贡献率.

4.2 对采暖期与非采暖期各自使用回归树方法,利用相对湿度、气压、风速等要素进行组合气象分类,根据PM2.5浓度均值划分等级.

4.3 以沈阳市为例进行实证分析.在采暖期,气象分类下的ARIMA+SVM组合模型的平均绝对误差小于0.6,与实际值相关系数大于0.7,正确率均值大于0.5;在非采暖期,组合模型的平均绝对误差约为0.4,与实际值相关系数约为0.5,正确率均值大于0.6.

[1] Tao J, Zhang L M, Zhang Z S, et al. Control of PM2.5in Guangzhou during the 16th Asian Games period: Implication for hazy weather prevention [J]. Science of the Total Environment, 2015,508:57－66.

[2] 孙宝磊,孙 暠,张朝能,等.基于BP神经网络的大气污染物浓度预测 [J]. 环境科学学报, 2017,37(5):1864-1871.

[3] 薛文博,付 飞,王金南,等.中国PM2.5跨区域传输特征数值模拟研究 [J]. 中国环境科学, 2014,34(6):1361-1368.

[4] 雷孝恩,韩志伟,张美根,等.城市空气污染数值预报模式系统 [M]. 北京:气象出版社, 1998:15-18.

[5] 张艺耀,苗冠鸿,闫剑诗,等.影响PM2.5因素的多元统计分析与预测 [J]. 资源节约与环保, 2013,(11):135－136.

[6] 尹建光,彭 飞,谢连科,等.基于小波分解与自适应多级残差修正的最小二乘支持向量回归预测模型的PM2.5浓度预测研究 [J/OL]. 环境科学学报:1-15[2018-03-13].https://doi.org/10.13671/j.hjkxxb. 2018.0093.

[7] 谢 超,马民涛,于肖肖.多种神经网络在华北西部区域城市空气质量预测中的应用 [J]. 环境工程学报, 2015,9(12):6005-6009.

[8] 黄 思,唐 晓,徐文帅,等.利用多模式集合和多元线性回归改进北京PM10预报 [J]. 环境科学学报, 2015,35(1):56-64.

[9] 陈亚玲,赵智杰.基于小波变换与传统时间序列模型的臭氧浓度多步预测 [J]. 环境科学学报, 2013,33(2):339-345.

[10] 陈 军,高 岩,张烨培,等.PM2.5扩散模型及预测研究 [J]. 数学的实践与认识, 2014,44(15):16-27.

[11] 周 丽,徐祥德,丁国安,等.北京地区气溶胶PM2.5粒子浓度的相关因子及其估算模型 [J]. 气象学报, 2003,61(6):761-768.

[12] 王黎明,吴香华,赵天良,等.基于距离相关系数和支持向量机回归的PM2.5浓度滚动统计预报方案 [J]. 环境科学学报, 2017,37(4):1268- 1276.

[13] 李 龙,马 磊,贺建峰,等.基于特征向量的最小二乘支持向量机PM2.5浓度预测模型 [J]. 计算机应用, 2014,34(8):2212-2216.

[14] 胡玉筱,段显明.基于高斯烟羽和多元线性回归模型的PM2.5扩散和预测研究 [J]. 干旱区资源与环境, 2015,29(6):86-92.

[15] Tai A P K, Mickley L J, Jacob D J. Correlations between fine particulate matter PM2.5and meteorological variables in the United States: Implications for the sensitivity of PM2.5to climate change [J]. Atmospheric Environment, 2010,44:3976-3984.

[16] Pateraki S, Asimakopoulos D N, Flocas H A, et al. The role of meteorology on different sized aerosol fractions PM10, PM2.5PM2.5-10[J]. Science of the Total Environment, 2012,419:124-135.

[17] 罗新兰,刘 源.沈阳地区相对湿度与PM2.5浓度对能见度的影响分析 [J]. 科学技术与工程, 2017,17(13):115-119.

[18] 杨 欣,陈义珍,刘厚凤,等.北京2013年1月连续强霾过程的污染特征及成因分析 [J]. 中国环境科学, 2014,34(2):282-288.

[19] 曾 静,王美娥,张红星.北京市夏秋季大气PM2.5浓度与气象要素的相关性 [J]. 应用生态学报, 2014,25(9):2695-2699.

[20] 王嫣然,张学霞,赵静瑶,等.北京地区不同季节PM2.5和PM10浓度对地面气象因素的响应 [J]. 中国环境监测, 2017,33(2):34-41.

[21] 朱倩茹,刘永红,徐伟嘉,等.广州PM2.5污染特征及影响因素分析,中国环境监测, 2013,29(2):15-21.

[22] 严文莲,周德平,王扬峰,等.沈阳冬夏季可吸入颗粒物浓度及尺度谱分布特征 [J]. 应用气象学报, 2008,19(4):435-443.

[23] 付桂琴,张杏敏,尤凤春,等.气象条件对石家庄PM2.5浓度的影响分析 [J]. 干旱气象, 2016,34(2):349-455.

[24] 曾乃晖,袁艳平,孙亮亮,等.基于聚类分析法的空气源热泵辅助太阳能热水系统气象分类研究 [J]. 太阳能学报, 2017,38(11):3067- 3076.

[25] 姜明辉,王 欢,王雅林.分类树在个人信用评估中的应用 [J]. 商业研究, 2003,(21):86-88.

[26] 傅传喜,马文军,梁建华,等.高血压危险因素logistic回归与分类树分析 [J]. 疾病控制杂志, 2006,10(3):256-259.

[27] 杨 敏,丁 剑,王 炜.基于ARIMA-SVM模型的快速公交停站时间组合预测方法 [J]. 东南大学学报(自然科学版), 2016,46(3):651- 656.

[28] 刘 杰,杨 鹏,吕文生,等.模糊时序与支持向量机建模相结合的PM2.5质量浓度预测 [J]. 北京科技大学学报, 2014,36(12):1694- 1702.

[29] 谢骁旭,袁兆康.基于R的江西省肺结核发病率ARIMA-SVM组合预测模型 [J]. 中国卫生统计, 2015,32(1):160-162.

[30] 王佳敏,张红燕.基于ARIMA-SVM组合模型的移动通信用户数预测 [J]. 计算机时代, 2014,(9):12-15+17.

[31] 程昌品,陈 强,姜永生.基于ARIMA-SVM组合模型的股票价格预测 [J]. 计算机仿真, 2012,29(6):343-346.

[32] 李晓岚,马雁军,王扬锋,等.基于CUACE系统沈阳地区春季空气质量预报的校验及修正 [J]. 气象与环境学报, 2016,32(6):10-18.

ARIMA-SVM combination prediction of PM2.5concentration in Shenyang.

SONG Guo-jun1, GUO Xiao-dan1*, YANG Xiao1, LIU Shuai2

(1.School of Environment, Renmin University of China, Beijing 100872, China；2.Agricultural Management Institute of the Ministry of Agriculture and Rural Affairs, Beijing 102208, China)., 2018,38(11)：4031~4039

Firstly, meteorological types of heating period and non-heating period were classified using the method of regression tree classification, and meteorological types which are likely to cause severe pollution were identified. Secondly, the daily mean value prediction model of PM2.5concentration of different meteorological types was established using the combination of Autoregressive Integrated Moving Average Model and Support Vector Machine (ARIMA+SVM), which takes the emission of pollution sources as independent variables. In this paper daily mean PM2.5concentration of 9environmental monitoring points with continuous data in Shenyang during Jan 2013 to June 2017 was analysed. The results show that, compared with ordinary machine learning model without weather classification, the prediction of daily mean PM2.5concentration using ARIMA+SVM combined model based on meteorological classification has a better agreement with actual value, and its ability to identify the peak and valley values is much stronger. In heating and non-heating period, this combined model has the advantages of lower average error and higher prediction accuracy.

PM2.5concentration；meteorological classification；ARIMA+SVM combination model；prediction method

X513

A

1000-6923(2018)11-4031-09

宋国君(1962-),男,黑龙江东宁人,教授,博士,主要从事环境政策管理研究.发表论文200余篇.

2018-04-04

国家重点研发计划项目(2017YFC0212500)

* 责任作者, 博士研究生, 15811440711@163.com