基于定性趋势分析的空调系统传感器故障检测

，，

(中国西昌卫星发射中心，四川 西昌 615000)

0 引言

空调系统中存在大量的温度、湿度、风速、压力、压差等传感器，这些传感器是空调系统参数检测的首要环节。如果没有传感器对原始参数进行准确可靠的测量，就无法实现信号的转换和信息处理、完成最佳数据的显示和控制[1]。一旦传感器发生故障，轻则引起不必要的能源浪费、降低室内空气品质，重则导致设备损坏，引发安全事故[2-3]。传感器由于工作环境复杂、分布面广、数量大、安装部位特殊等，往往成为空调系统的薄弱环节。由于自然的或人为的因素，传感器随时都可能发生故障。目前，人工检测与定期校准检定仍然是发现传感器故障的主要途径，但此方法拆卸麻烦、工作量大、效率低，不能及时发现故障，因此进行传感器故障检测研究非常必要。

空调系统传感器数量庞大，一般会有多个传感器的信号曲线具有一定的相似性，因此可以利用传感器数据间的相似性进行故障检测，当某一传感器的数据曲线与其他传感器曲线不再相似时，表明该传感器发生了故障。定性趋势分析法能自动分析传感器数据，判断传感器数据间相似性以实时检测传感器故障。

1 故障检测构架及原理

空调系统中有多个传感器的信号曲线具有一定的相似性。把信号曲线相似的传感器分成一组，利用同一组中传感器数据的相似性进行故障检测。故障检测构架如图1所示，采集数据预处理，趋势提取、识别，趋势匹配和故障检测是构架中的四大主要环节[4]。采用趋势提取识别算法，将传感器数据转换成趋势，用模糊趋势匹配算法将传感器趋势两两相匹配。正常情况下，同一组中两两传感器趋势匹配度SIij较大。若某一时段，某一传感器与其他传感器的趋势匹配度明显下降，即SIi*<设定值(如0.5)，则说明传感器i发生故障。

2 定性趋势分析

2.1 趋势语言

定性趋势描述语言为用一阶导数和二阶导数符号表示的七种基元[2]，如图2所示。

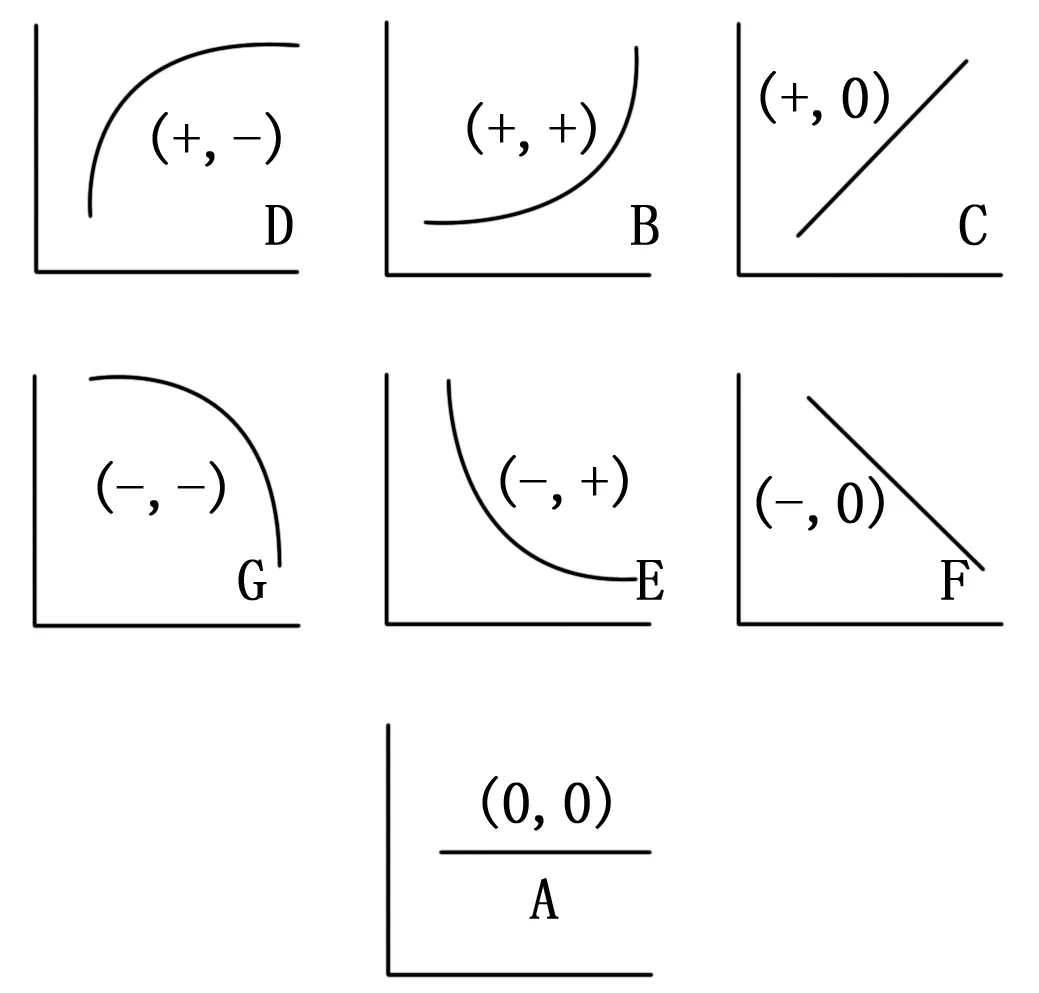
图2 基元

2.2 数据预处理

(3.1)

式中，yi为信号幅值，yi,降噪为信号降噪后的信号幅值，N为总采样点数。因此，首先要对采集的数据进行降噪处理。

故障诊断中，分析的通常是混有白噪声的非平稳信号，传统的降噪方法对此类信号的处理有一定的局限性，常常会将含有故障特征的微弱信号滤除，造成故障漏检。近年来发展起来的小波分析由于具有可进行时频域同时局部分析的特点，能够很好地抑制非平稳信号中的噪声并且保留原始信号的特征，在信号降噪领域得到了越来越广泛的应用。因此，本文采用小波降噪法进行数据的降噪。

2.3 趋势提取

实时趋势演变速率快慢不一。因此，很难确定识别时间窗的宽度——宽度太宽或太窄都会造成趋势的误识别。任意能准确捕捉到趋势实时演变的趋势识别技术，其识别时间窗都不应该是固定的。识别时间窗应该既宽到能观测到监控信号的变化，又小到用一个基元就能很好地描述信号。区间半分法能根据实时趋势的演变速率，自动调节识别时间窗的宽度，本文采用区间半分法自动提取趋势。

Yk=[y(tki)，y(tki+ΔT)，…，y(tki+(mk-1)ΔT]τ

两个连续单峰片段的近似多项式不一定连续，为了确保近似数据的连续性，一旦识别了一个单峰片段，就要用约束多项式拟合方法优化近似多项式(包括阶次和系数)。下面介绍约束多项式拟合数据算法。

对β1,β2,λ,μ求偏导数，并使之为零，得:

至此将传感器数据转换为拟合多项式序列。

y(t)={y1,y2,…,yN}→y(t)≈{Q1(t),Q2(t),…,QM(t)}

区间半分法流程如图3所示。

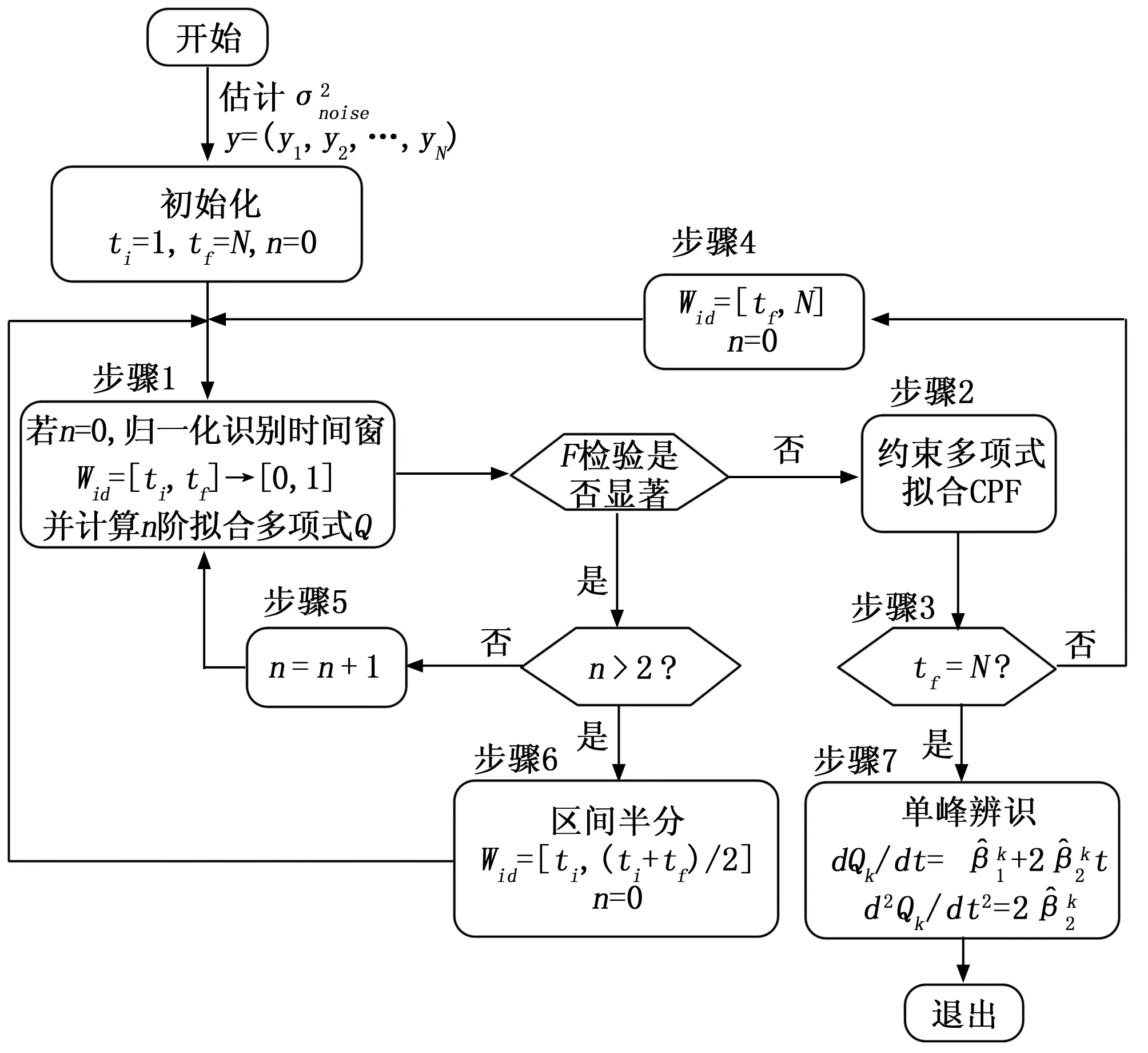
图3 区间半分法流程图

根据多项式的导数符号可识别基元，将多项式序列转换为基元序列[8]：

y(t)≈{Q1(t),Q2(t),…QN(t)}→Tr={P1,P2,…PN}

2.4 趋势匹配

采用上述算法得到基元序列后，可以将相互关联的传感器趋势进行匹配，根据趋势的匹配程度检测传感器是否发生故障。下面介绍趋势匹配算法：1)基元匹配；2)趋势匹配；

2.4.1 基元匹配

基元是趋势的基本组成单位，首先要考虑基元间的相似度。基元具有相似性，如基元A和C、F相似，基元B和C、D相似，因此可以把基元模糊归类[9]。定义基元Pi和Pi*的相似度如表1所示。

2.4.2 趋势匹配

将传感器数据转换成趋势后，即y(t)={y1,y2,…,yN}

表1 基元相似度矩阵

→Tr={P1,P2,…,∧PN},就可以将传感器趋势进行匹配，求出他们之间的匹配程度[10]。可以从两个方面估计趋势的相似度：基元的顺序；基元的持续时间。定义趋势相似度为：

此匹配算法只考虑了基元的顺序，是不严密的。为了更准确的区分趋势，还应考虑基元的持续时间，即匹配区间长度Δtui=tui-tui-1。匹配区间较长的基元相似度比匹配区间较短的基元相似度所占权重要大些，即:

为了使两趋势具有尽可能大的相似度，定义趋势相似度为:

SI=max[SI1，SI2]

2.5 故障检测

分析系统正常工况条件下的传感器趋势，将信号曲线相似的传感器分成一组，得到若干组传感器。将同一组中的传感器趋势进行两两比较分析，得到SIij。由于同一组传感器趋势是相似的，所以传感器的趋势匹配度即SIij较大。若传感器发生故障，则传感器的趋势必然会发生较大的变化 ，传感器的趋势与其他传感器趋势不再相似，与其他传感器的匹配度SIi*也会变小。所以，若某一时段，某一传感器与其他传感器的趋势匹配度明显下降，如SIi*<设定值(如0.5)，则说明传感器发生故障。

传感器发生阶跃偏置故障的时间较短，SIi*变化不明显，但包含阶跃偏置故障点的单峰片段的一阶导数绝对值会偏大，可设一阶导数值的绝对值阈值为d1th，若|d1|>d1th，则传感器发生故障。故障检测流程图如图4所示。

本文利用同一组中传感器两两趋势的匹配度进行故障检测，趋势匹配的计算量会随着同一组中传感器数量的增加而呈几何级数增加，给故障检测带来极大的挑战。因此，传感器分组时应当控制同一组中传感器的个数。

3 空调系统

空调系统为全新风直流式系统，采用定风量变露点自动控制，特点是送风量不变。通过改变送风温湿度来满足室内负荷变化。其暖通部分由新风预处理系统、空调后处理系统、制冷系统3个子系统组成，如图5所示。新风机组和转轮除湿机组共同组成新风预处理系统，新风预处理系统对新风进行初步调节，使之接近最终目标；空调后处理系统，对空调送风进行温度和湿度的精细调节，是送风满足室内负荷要求。空调系统由表冷器、加热器、加湿器、除湿机、新风机、送风机、变频器、新风阀、送风阀、风管等组成。

表2 表冷器2温度传感器正常工况下基元一阶导数值

图4 故障检测流程图

图5 空调系统结构图

分析空调系统各传感器数据，得知表冷器2温度、机组电加热温度、风管电加热温度、送风温度的数据虽不相同，但曲线很相似，如图6所示，因此将其分为一组进行定性趋势分析。

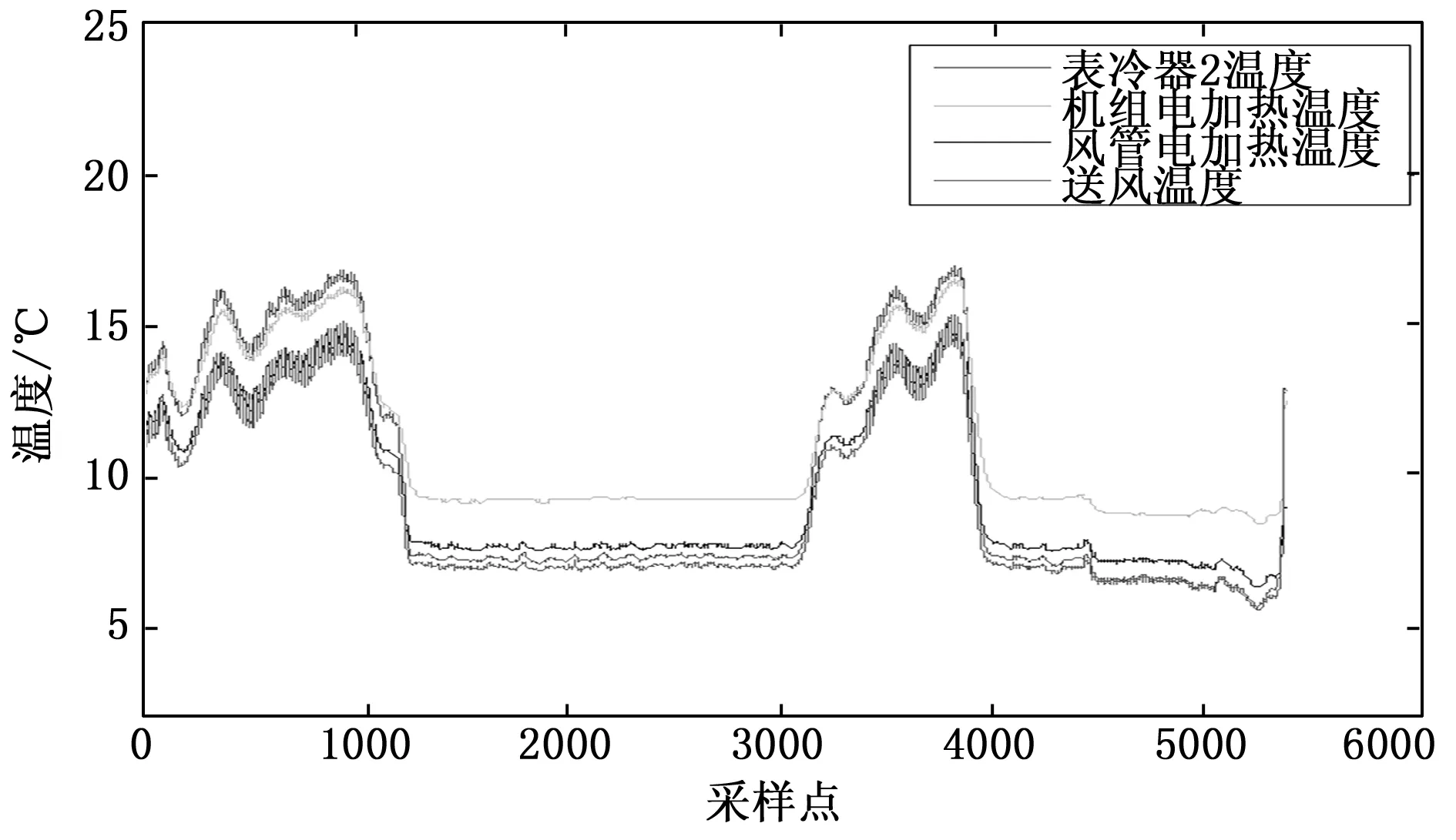
图6 空调系统各传感器数据曲线图

4 仿真研究

传感器故障都可以等效为漂移故障或偏置故障，本文主要对传感器的漂移和偏置故障进行实验[11]。采集空调系统正常工况下某一时段各传感器数据，采样周期为2 s，得到8 000组采样数据。研究表冷器2温度、机组电加热温度、风管电加热温度、送风温度的趋势相似度，设趋势匹配时间长度为20 min，即600组采样数据，按照先进先出的原则每2 min匹配一次，得到两两间的趋势相似度SIij>0.8，表明正常工况下两两间的趋势很相似。

表冷器2温度传感器正常工况下基元的一阶导数值如表2所示。从表中可以看出，表冷器2温度传感器基元一阶导数值分布区间为[-1.1008 1.4611 ]，因此令一阶导数值的绝对值阈值为d1th=2.0。

4.1 漂移故障

当表冷器2温度传感器在采样点3 000点处发生漂移率为-0.004采样点的漂移故障时，趋势匹配图如图7所示。在3 000点附近，表冷器2温度传感器与其他传感器的相似度SId*显著下降，远远小于0.5，而其他传感器趋势无明显变化，表明表冷器2温度传感发生了故障。从4 080点到5 080点趋势匹配度SId*比较大，这是因为其他传感器也表现为下降趋势。

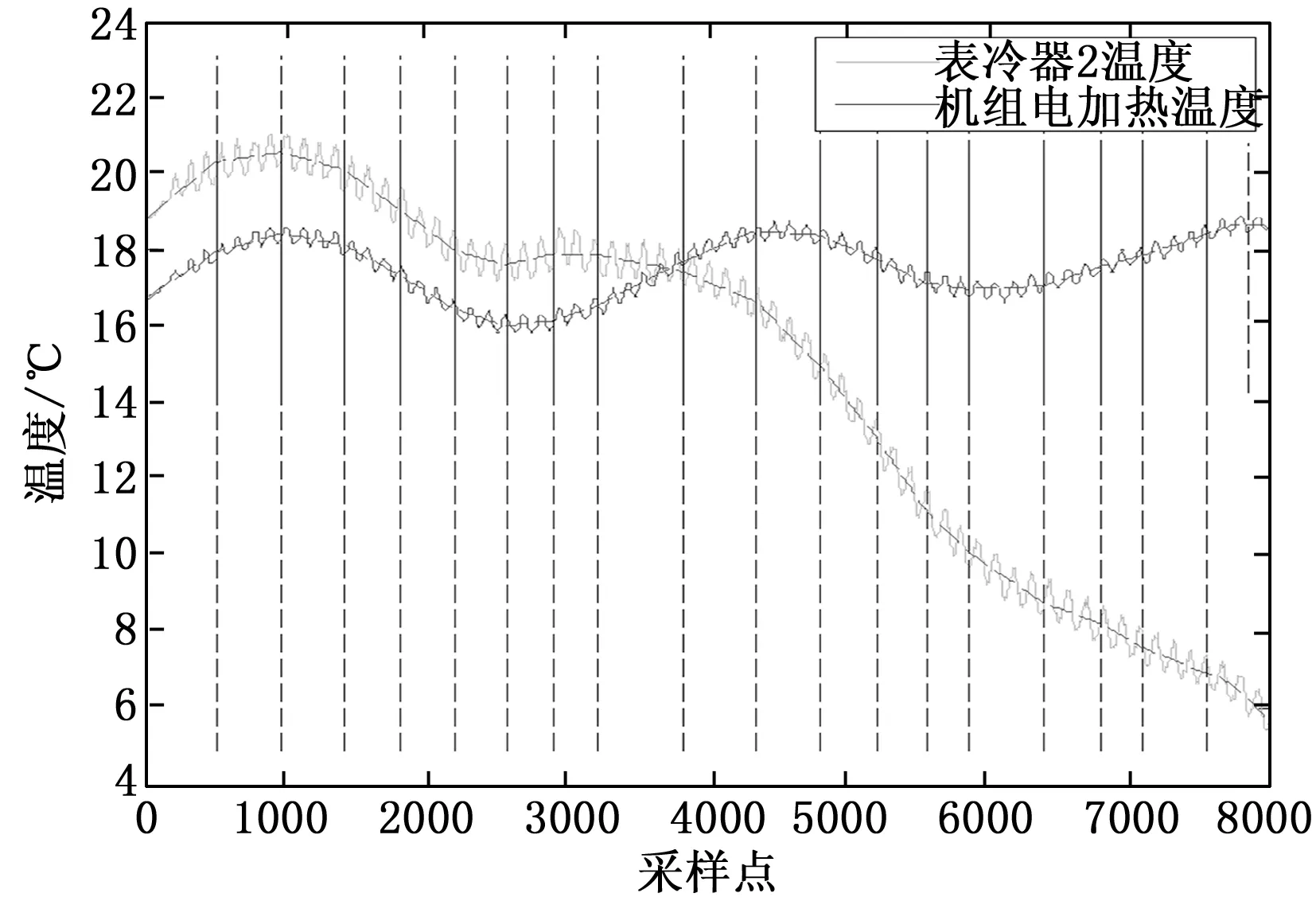
图7 表冷器2温度传感器发生漂移故障趋势匹配图

表3 表冷器2温度传感器发生偏置故障时基元一阶导数值

4.2 偏置故障

当表冷器2温度传感器在采样点3 000点处发生偏置量为4的偏置故障时，趋势匹配图如图8所示。趋势匹配度如表3所示。从表中可以看出，当分别发生偏置量为4、2、-2的偏置故障时，故障发生点处的一阶导数值为d1+4=5.8999、d1+2=3.2359、d1-2=-2.0921，d1th=2.0，|d1+4|>d1th，|d1+2|>d1th，|d1-2|>d1th，都检测出后表冷后温度传感器发生了故障。

图8 表冷器2温度传感器发生偏置故障趋势匹配图

5 结论

本文提出基于定性趋势分析的传感器故障检测方法，该方法针对空调系统中存在多个传感器信号相似的特点，将信号相似的传感器分成一组，利用组间传感器信号的相似性进行故障检测。通过对传感器的两种典型性故障即漂移故障和偏置故障进行仿真实验，结果表明定性趋势分析方法能及时检测故障。