基于双层规划模型的滑行道与停机位再指派联合调度

2018-11-28姜雨徐成蔡梦婷陈丽丽

北京航空航天大学学报 2018年11期

姜雨，徐成，蔡梦婷，陈丽丽

(南京航空航天大学民航学院，南京 210016)

民航需求日益增大，延误航班日益增多。航班延误往往导致停机位预指派计划无法正常实施。同时停机位指派结果的改变将影响滑行调度的起讫点，进一步增加了其复杂度，对停机位和滑行道联合调度提出了更高的要求。

国内外学者已经对停机位与滑行道的联合调度进行了大量研究，研究成果颇为丰富。目前，研究成果主要分为单资源系统调度和多资源系统调度2类。在单资源系统调度方面，国内外学者建立了考虑滑行调度影响的停机位指派模型[1]，部分学者采用车间调度[2]、预测[3-4]等手段得到航空器滑行时间，并以滑行时间作为停机位指派模型的输入变量，建立考虑停机位指派影响的滑行道调度模型[5-6]，或是引入停机位推出时间控制策略建立滑行道调度模型进一步提升滑行道运行效率[7-8]。在多资源系统调度方面，则主要建立分步骤的滑行道与停机位多系统调度模型[9-10]，按照先进行停机位指派再进行滑行道调度的顺序进行场面优化[11]，并在此基础上允许路径选择[12-13]。部分学者尝试在滑行道调度采用固定路径的基础上进行停机位指派最终实现航空器无冲突滑行[14]。此外，部分学者采用仿真软件进行相关研究，如采用CPN Tools仿真航班过站时跑道与停机位的利用情况，探索如何提高场面资源利用率[15]，基于JADF(Java Agent Development Framework)平台开发机场空侧仿真系统，对跑道入侵与滑行冲突进行风险控制[16]等。

纵观国内外研究成果，单资源系统调度对滑行调度或是停机位指派有较大简化，侧重于对单一资源系统深入的研究。现有的多资源系统调度则主要采用先进行停机位指派再进行滑行道调度的分步骤的建模方式，难以体现停机位指派与滑行道调度之间的反馈作用。如何在保障滑行道和停机位指派质量的基础上实现联合调度这一问题亟待研究。

本文以滑行道调度为上层规划，停机位再指派为下层规划，建立滑行道和停机位联合调度双层规划模型。在提高停机位和滑行道运行效率的同时减少航空器整体等待时间和停机位受扰动影响，并设计遗传算法结合MATLAB对所建双层规划模型进行验证。

1 滑行道和停机位再指派双层规划模型建模

本文采用无向图G(V,E)对机场场面网络进行建模，其中V为节点集合，E为边的集合，并以航空器在无向图中的运行过程为研究对象建立停机位和滑行道双层规划模型。

1.1 基于滑行道调度的上层模型

上层模型为滑行道调度模型，滑行道调度基于停机位再指派结果，是场面调度规划的上层模型。地面管制员将离场航空器由停机坪出口点经滑行道滑行引导至跑道入口点排队，将进场航空器由跑道出口点引导至停机坪入口点。具体模型如下：

minZ1=

(1)

s.t．

(2)

(3)

(4)

∀i,j∈FA∪FD，bnij=1

(5)

(dmnitmi-dnmjtmj)(dmnitni-dnmjtnj)≥0

(6)

(dmnitmi-dmnjtmj)(dnmitni-dnmjtnj)≥0

(7)

(8)

(9)

(10)

1.2 基于停机位再指派的下层模型

下层模型为停机位再指派模型。下层模型确定待调度航空器的具体停机位及其所属停机坪，由此确定上层模型航空器滑行道调度中的起点和终点。下层模型目标函数如下：

(11)

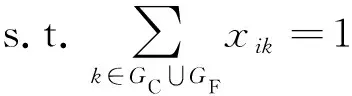
(12)

xikεij=xjkεij∀i∈FA,∀j∈FD

(13)

(14)

Mixik≤Nk

(15)

目标函数式(11)表示最小化远(GC)和近机位(GR)更换扰动vik和wik，以及航空器进入停机坪的等待时间Tβτ最小。η为等待时间的权重，为常数，可由仿真得到；Tβτ来自上层模型求解结果,体现了上层模型向下层的数据传输；Mi为航空器i的机型；yiβτ为判断航空器i是否在τ时段进入停机坪β的布尔变量；xik为判断航空器i是否分配至停机位k的布尔变量。

2 算法实现

遗传算法具有算法参数少、流程简洁、编程易实现、求解效率高、计算量小等特点,在组合优化问题上有独特优势。本文采用遗传算法对模型进行求解，首先采用整数编码的方式，对从机场采集的数据按照时间顺序排序并进行编码。染色体结构如图1所示。

图1 染色体结构Fig.1 Structure of a chromosome

图1为滑行道调度染色体结构，每个染色体由FA+FD个基因组成。基因在染色体的位置代表航空器序号，基因的数值代表该航空器选取的路径编号。如第1个基因位置序号为1，值为R1，代表1号航空器的滑行路径编号为R1。停机位再指派模型中染色体结构与此相同，不再赘述。

本文结合双层规划模型在传统遗传算法基础上引入单点交叉与循环嵌套的迭代方式如下：

因基本交叉可能产生停机位指派与滑行道调度的不可行解,本文采用单点交叉的方式进行交叉操作。即随机选取染色体n1、n2片段n3∈[1,size]，概率p∈(0,1)，如果p

本文采取循环嵌套的迭代方式以契合双层规划模型。即本文算法先进行ig次停机位再指派迭代并在此基础上对滑行道调度模型进行it次迭代，此为1次联立迭代，总计进行iG次联立迭代。其中每次联立迭代初始解均包含上一次联立迭代最优解。

本文设置适宜度为各模型目标函数，其余诸如选择与变异等操作原理均与传统遗传算法相同，此处不再赘述。

3 仿真验证

本文以中国华东某大型机场为例进行仿真实验。本文依据该机场提供的2016年3月11日8:00—12:00的机位预指派计划表，对40个航班对及其对应的80架进离场航空器进行停机位再指派和滑行道调度。

本文将G1～G34共34个停机位归类在C1～C8共8个停机坪中，形成如图2所示的机场场面网络无向图。图中R1、R2为跑道节点，A1～A16为非停机坪区域滑行道节点，B1～B9为停机坪区域的滑行道节点。B1～B3、B4～B6、B9～B7及停机坪区域内的滑行道为停机坪区域滑行道。C1～C5的出入口分别为B1～B5；C6的出入口为B6；C7的入口为B7，出口为B8；C8的入口为B9，出口为B8。根据各停机坪距离跑道出入口的距离设置C1～C6为近机位停机坪，C7和C8为远机位停机坪。

停机位信息及预指派计划如表1和表2所示。

表2中,ETA(Estimated Time of Arrivals)为预计进场时刻，ETD(Estimated Time of Departures)为预计离场时刻。仿真测试中算法参数为：滑行道调度种群数目设为50，停机位再指派问题种群数目为100，突变概率0.02。对上层模型滑行道调度问题迭代100次，下层模型停机位再指派问题迭代150次，联立迭代次数为20次。依据实际运行情况设置:ut=15 m/s，ug=10 m/s，Tent=60 s，Tpush=300 s，uf=50 m，Tmax=250 s。

停机位仿真结果如图3所示，滑行道仿真结果如图4所示，停机位再指派模型前15代进化程度剧烈。随着迭代代数的增加，目标函数逐渐降低，扰动值逐渐升高最终在一个合理的范围。滑行道调度前30代收敛速度较快，80代后趋于稳定，这说明本文所取迭代代数是足够的。

本文采用2种方式进行联立迭代：每次迭代时仅参考前一次迭代结果的反馈和参考历次累积迭代结果的反馈。仿真结果如图5和图6所示。

图2 机场场面网络无向图Fig.2 Undirected graph of airport surface network

停机位号停机坪号机型G1C1DG2C1CG3C1CG4C1DG5C2CG6C2CG7C2CG8C2DG9C3DG10C3CG11C4CG12C4DG13C4CG14C4CG15C5CG16C5CG17C5CG18C5DG19C6CG20C6CG21C6CG22C6CG23C6CG24C7DG25C7DG26C7DG27C7DG28C7CG29C8CG30C8CG31C8CG32C8CG33C8CG34C8C

表2 停机位预指派计划Table 2 Gate pre-assignment plan

图3 停机位再指派迭代趋势Fig.3 Iteration trend of gate re-assignment

图4 滑行道调度趋势Fig.4 Trend of taxiway scheduling

图5 仅考虑前一次迭代结果的仿真结果Fig.5 Simulation results only considering the last iterative result

图6 考虑历次累积迭代结果的仿真结果Fig.6 Simulation results considering all previous cumulative iteration results

图5显示，仅考虑前一次迭代结果的反馈方式不具有稳定性，而考虑历次累积迭代结果的反馈方式具有明显的趋势性(见图6)，可见考虑历次累积反馈方式具有较好的反馈效果。因此本文采取该迭代方式进行仿真。

迭代后期的双层模型求解结果，基于人工停机位再指派的双层模型求解结果和采用理论最短滑行路径的双层模型求解结果的对比如表3所示。

可见，在人工指派将较多的航空器指派至远机位，导致平均滑行时间增长,航空器平均滑行时间高于迭代后期的结果,冲突增加达75%，严重影响场面运行效率。相比于人工指派，双层规划策略停机位扰动值由441降至325，降低了26.3%，平均滑行时间由121.65 s降低至91.86 s，降低了24.49%，优化效果明显。在滑行道调度使用最短路径的情况下，不仅产生49次冲突，还产生滑行路径锁死的情况，远高于其他类型的仿真结果,不能应用于实际调度。

对迭代后期的实验结果进行分析，结果如表4和图7所示，表4中记录不同指派方案受扰动航空器被指派至的停机位序号。

迭代后期的停机位再分配共影响6架航空器，其中30号航空器被指派至远机位34，其余5架航空器再指派与预指派间隔8.625个停机位，处于旅客可接受的范围。更换的停机位与原停机位处于不同的停机坪，减少了停机坪冲突发生的可能性。迭代后期的仿真结果显示滑行道调度过程中，大部分航空器滑行时间在150 s以内。经统计，最短路A1～A11使用频率最高，而远机位停机坪C8仅有1架航空器经过，多数航空器的滑行路径较短。总计27架航空器选取最短路径，占总航空器数的33.75%；有8架航空器选取了迂回的路径，占总航空器数的10%，其他航空器均选取了较短的路径。迂回路径和较短路径的选择有效避免了滑行路径冲突，减少了冲突时间。滑行道冲突情况如表5所示。