一种复合方法抑制叶尖泄漏的试验及模拟研究

2018-11-28胡建军张铎张香兰孔祥东

北京航空航天大学学报 2018年11期

胡建军，张铎，张香兰, 孔祥东

(1. 燕山大学机械工程学院，秦皇岛 066004; 2. 燕山大学建筑工程与力学学院，秦皇岛 066004)

涡轮叶顶间隙的存在使得流体工质在叶片压力面和吸力面压差驱动下产生叶尖泄漏流(Tip Leakage Flow, TLF)，这对整个叶栅通道的流场特性和流动损失均产生了重要影响[1-2]。根据是否需要外界能量输入，叶尖泄漏控制可分成主动控制和被动控制2种。

在叶尖泄漏主动控制技术方面，van Ness[3]和李钢[4]等利用离子体放电控制泄漏流，改善了总压损失和流动阻塞；何育军等[5]提出了一种双闭环主动快速控制系统，研制出一种能主动控制叶顶间隙高度变化的作动装置；牛茂升[6]对采用叶顶主动喷气控制叶栅通道内流场特性进行了研究，比较了不同喷气参数对泄漏流的抑制效果；徐逸钧等[7]搭建了一套可控热变形机匣模型试验证台，研究了变工况下机匣的变形量及其对叶尖泄漏的抑制作用。目前，主动控制虽然已经展示出了很好的控制效果，但由于执行机构复杂、可靠性低、需要额外能量等缺点，还停留在基础研究阶段。

被动控制一般通过对叶尖或机匣进行几何改型来实现，例如在叶尖加装叶冠[8-10]、改变叶尖形状[11-13]或对机闸进行造型[14-16]等。虽然一些被动控制方法已经得到了工程应用，但在变工况时被动泄漏抑制的效果还不是很理想；另外，叶尖几何改型对间隙变化非常敏感[13]，间隙增大后泄漏抑制效果急剧恶化。

被动式气动封严是另外一类有应用前景的叶尖泄漏控制方法。与叶尖几何改型控制方法相比，气动封严方法不受转、静部件剐蹭的机械限制，对转、静之间的间隙也不敏感。1995年，Auxier[17]提出根据叶片表面压力分布特点，自发生成一股气流用于叶尖泄漏控制的想法，其主要原理是利用逆向自发射流(Spontaneous Tip Injection,STI)阻滞泄漏流动，从而达到减小泄漏量的目的。2007年，维也纳科技大学的Hamik和Willinger[18]根据该原理提出一种具体的开孔方案，并对性能潜力进行了分析。2013年起，胡建军等[19-20]通过实验和数值模拟手段分析了三维叶栅模型下自发射流与叶尖泄漏流相互作用特性及其泄漏抑制效果。

为了获得更优的叶尖泄漏抑制效果，本文提出将被动式气动封严与叶尖几何改型相结合用于抑制叶尖泄漏及其损失。然而，叶尖几何改型方案众多，本文选取了自发射流与叶顶凹槽耦合以体现代表性。根据自发射流出口与叶顶凹槽的相对位置不同，构建了3种典型耦合方案，对比了不同耦合方案的泄漏抑制效果。通过分析不同方案的间隙泄漏特性和流场分布，筛选出了耦合特性良好的方案，并探讨了叶顶凹槽耦合自发射流的泄漏抑制机理。

1 试验模型及测量结果分析

试验模型以Durham平面叶栅为原型[21]，如图1(a)所示。由于本文主要考察自发射流与叶顶凹槽耦合对叶尖泄漏的抑制效果，因此沿着叶顶泄漏流动方向从三维模型上剖切出一段，形成一个准二维模型用于初步考察不同耦合方案的泄漏抑制效果，暂不考虑叶栅通道内三维流动的影响。通过在叶片前缘附近截取一段轴向弦长10 mm且带有1个自发射流孔道的部分得到准二维的试验及数值模型，如图1(b)、(c)所示。

图1 叶顶凹槽耦合自发射流的数值模型和试验模型Fig.1 Numerical and experimental model of tip groove coupled with STI

试验模型基于相似原理进行了设计，如图1(b)所示，而数值模型与试验模型保持完全一致，如图1(c)所示。由于待测试验模型内流动不存在自由液面，故不考虑表面张力的作用。重力与压缩性对流场的影响也可忽略，故不考虑韦伯相似、弗劳德相似及马赫相似。而在试验模型中，黏性力、压力和惯性力起主导作用，故本试验模型在满足几何相似条件下，其动力学相似的决定准则数取雷诺数，表达式如下：

(1)

式中：ρ为流体密度，kg/m3；υ为流速，m/s；L为特征长度，m；μ为动力黏滞系数，Pa·s；Re为雷诺数；下标p和m分别代表原型和试验模型。

基于间隙内流动相似，最终确定了试验模型叶顶间隙尺寸相对于原始模型放大10倍，叶顶间隙高度达到10 mm，模型整体外廓尺寸为300 mm×40 mm×30 mm。其中，厚度方向30 mm中，腔内厚度为10 mm，其余为有机玻璃壁厚。试验工质由空气替换为水。

采用粒子图像测速(Particle Image Velocimetry, PIV)技术对试验模型的流场进行测量，除了可以揭示耦合方案的间隙流场特征，还可以用于验证数值模型正确性。搭建了叶顶凹槽耦合自发射流流场测量试验台，如图2所示。试验系统主要由离心式水泵(QDX3-20-0.55)、变频调速器(DELIXI 0.75 kW,0～50 Hz,±0.01 Hz)、示踪粒子水箱(聚苯乙烯球作为示踪粒子，平均直径20 μm)、待测试验块、2D-PIV流场测量系统、NI数据采集系统、连接软管及阀门等组成。

图2 试验系统Fig.2 Experimental system

该2D-PIV流场测量系统详见文献[20]，系统的测量误差约为1%。试验中，通过变频调速器调节水泵转速来改变试验模型的入口流量，根据试验模型内主要测量区域的流速，结合文献[22]的试验方法，可以确定试验中双脉冲的跨帧时间。

本文除了对图1(b)所示试验模型开展了流场测量外，还测量了2种基本型叶尖结构的间隙及其下游流场，分别为纯自发射流模型(见图3(a))和纯叶顶凹槽模型(见图3(b))，用于开展对比研究，以期揭示2种被动抑制方法的耦合机理。

图3(a)为纯自发射流模型及其测量结果。观察可知，叶尖射流出口处确实产生了自发射流，该股射流逆着泄漏流方向流出，通过掺混作用耗散泄漏流动能。同时，在自发射流的挤占作用下，间隙内流线上拱，流道断面收缩，预期可对泄漏流产生一定抑制作用。

图3(b)为纯叶顶凹槽模型及其测量结果。观察可知，凹槽内流体在非对称流体剪切作用下形成凹槽涡(Groove Vortex, GV)，该旋涡在与凹槽内壁面的摩擦过程中会不断损失动能，而损失的动能又只能不断地由新进入的泄漏流进行补充，这就变相地消耗了泄漏流的动能，导致泄漏流减速，预期可以对泄漏流产生一定抑制作用。此外，凹槽涡的存在也导致了间隙流线上拱，挤占了泄漏流通道，预期能对泄漏抑制有所贡献。

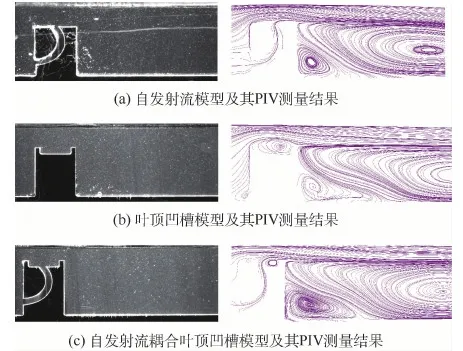
图3 3种叶尖模型及其流场测量结果Fig.3 Three models of turbine tip and their flowfield measurement results

图3(c)为自发射流耦合叶顶凹槽模型及其测量结果。在这种耦合方案下，原本存在于凹槽中的单个大尺度凹槽涡遭到破坏，被自发射流分割为左右2个小旋涡，而且2个旋涡的强度显著不同。其原因在于左旋涡旋向与射流方向相逆，两者抵消，导致旋涡强度较弱；右旋涡旋向与射流方向一致，旋转得到强化，因此强度较强。此外可以料想，自发射流在穿出凹槽的过程中，动能也会部分地被耗散，因此该耦合方案是否能取得比单一控制方法更优的抑制效果，如何耦合才能获得最优的泄漏抑制效果，尚需进一步计算确定。

2 数值模型及其正确性验证

本节以凹槽-中间自发射流模型为例，阐述建模过程和正确性验证方法。采用ICEM CFD 软件进行几何建模和分块结构化网格划分，如图4所示。考虑到流场的对称性，只对试验模型的二分之一进行建模，中截面设定为对称面。为提高计算精度，分别对近壁面、叶顶间隙和自发射流流道网格进行了加密。

以模型总入口质量流量为指标对数值模型进行网格无关性检查，结果如图5所示。结果表明，当网格数量超过90万时，入口质量流量变化明显趋缓，质量流量的变化率已经小于0.3%。考虑到计算精度和计算代价的平衡，最终选取计算网格数为90万。无量纲壁面距离y+为10～40，壁面函数选择non-equilibrium wall function。

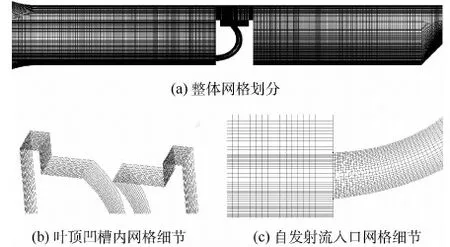
图4 数值模型的网格划分Fig.4 Grid partition of numerical model

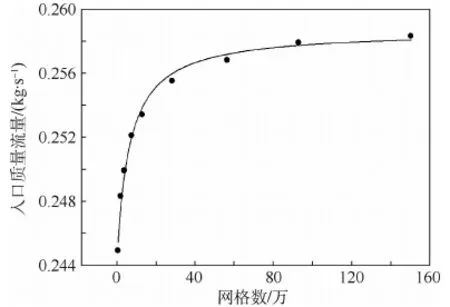
图5 网格独立性检查Fig.5 Grid independence check

采用商业程序ANSYS FLUENT 14.0数值求解雷诺时均Navier-Stokes方程，采用二阶迎风格式离散对流项，中心差分格式离散扩散项，采用基于Simple算法的数值求解方法和分离式求解器。计算中边界条件设定与试验保持一致，工质为水，进出口分别设置为Pressure inlet和Pressure outlet，中截面设置为Symmetry，其他壁面设定为wall。计算过程中，除能量方程残差下降6个数量级外，其他方程残差下降5个数量级视作收敛。

为了确定数值计算的湍流模型，分别采用4种湍流模型(一方程的S-A模型、两方程的k-ε-Standard模型、k-ω-Standard模型和七方程的Reynolds Stress Model模型)对流场进行试算，并与试验结果进行对比，如图6所示。计算结果表明，k-ε-Standard模型最为准确地预测了流场特性，其涡系结构、旋涡位置、速度大小与试验测量结果最为接近。故最终选用k-ε-Standard模型作为数值计算的湍流模型。

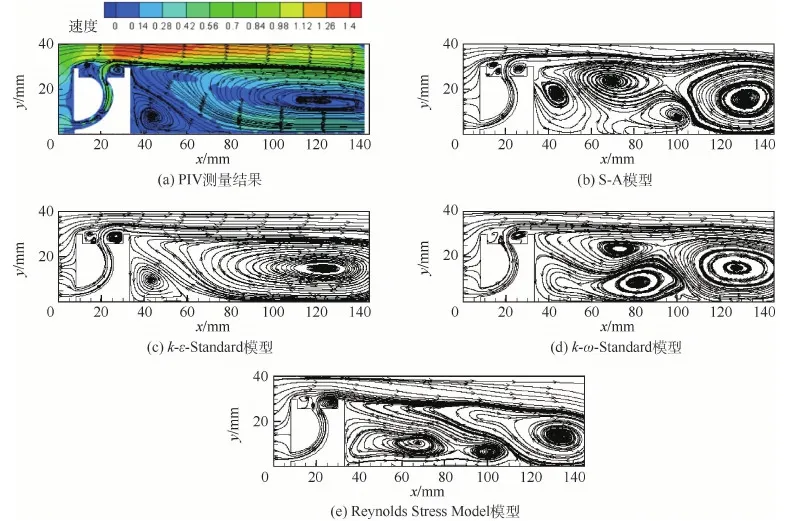
图6 试验结果与数值结果比较Fig.6 Comparison between experimental and numerical results

3 计算结果分析与讨论

PIV测量结果的分析表明，叶顶凹槽与中间射流的耦合较为不利。为了对比不同耦合方案的泄漏抑制效果，筛选出更优的耦合方案，本节运用数值手段对2种单一控制方法和3种耦合方案的流场特性进行研究，以期获得其抑制效果产生差异的原因。

本节构造了3种典型的叶顶凹槽与自发射流耦合模型(见图7)，分别为：自发射流出口在压力面侧(见图7(a))、自发射流出口在凹槽内(见图7(b))及自发射流出口在吸力面侧(见图7(c))。3个模型的叶顶间隙高度固定，均为10 mm。考虑到加工的便利性，自发射流内部通道的断面为4 mm×10 mm矩形。叶顶凹槽的深度均为4 mm，凹槽肋的宽度根据自发射流出口位置的不同略有调整，最薄的出现在凹槽中间射流情形，两侧肋厚均为3 mm。

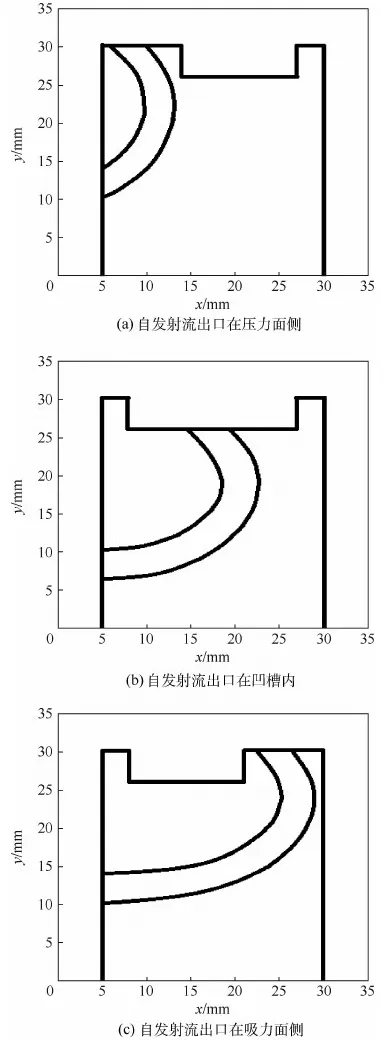
图7 叶顶凹槽与自发射流耦合的3种典型方案Fig.7 Three typical schemes of tip groove coupled with STI

3.1 不同方案泄漏抑制效果对比

以单一被动抑制叶型(纯自发射流与纯叶顶凹槽)为基准，比较了5种方案的泄漏抑制效果，如图8所示。其中横坐标为压比，定义为入口总压/出口静压，纵坐标为叶顶间隙泄漏质量流量，取叶顶间隙出口质量流量，即包含了叶顶间隙进口流量和自发射流流量。

图8的计算结果表明，在所研究的压比范围内，凹槽压力边自发射流与凹槽吸力边自发射流对泄漏流的抑制均好于纯叶顶凹槽模型，2种耦合方案相对于纯叶顶凹槽的抑制效果分别提升了17.51%和24.92%，而凹槽中间自发射流叶型的泄漏抑制效果反而不如纯叶顶凹槽模型。

与纯自发射流模型相比，只有凹槽吸力边自发射流叶型对泄漏流的抑制好于自发射流模型，泄漏量减少了5.61%。其他耦合方案的泄漏抑制效果均较自发射流模型差，表明不良耦合方案的泄漏抑制效果甚至不如单一抑制方法，即需要对耦合方案进行对比筛选。此外，耦合方案的泄漏抑制效果不如自发射流，也可能与本文模型的间隙高度较大有关。文献[13,19]的研究均表明，不同抑制方法对间隙高度变化的敏感度不同，叶顶凹槽对间隙变化较为敏感。本文通过相似计算将叶顶间隙从真实工况的0.5～1 mm放大到10 mm，在这样大的叶顶间隙下，凹槽的抑制效应大大削弱。同时，本文计算表明，自发射流方法的间隙高度敏感度较小。

3.2 单一抑制方法泄漏抑制机理分析

图9为纯自发射流和纯叶顶凹槽模型叶顶间隙内的流场分布。与图3(a)、(b)中的PIV测量结果相比，数值计算能够捕捉一些关键的流场细节，如自发射流模型间隙入口的分离泡(Separation Bubble, SB)、凹槽涡导致的间隙内流线上拱现象等，再次验证了所建数值模型的正确性，而且由于叶尖射流的存在，使得间隙进口分离泡范围有明显扩大。

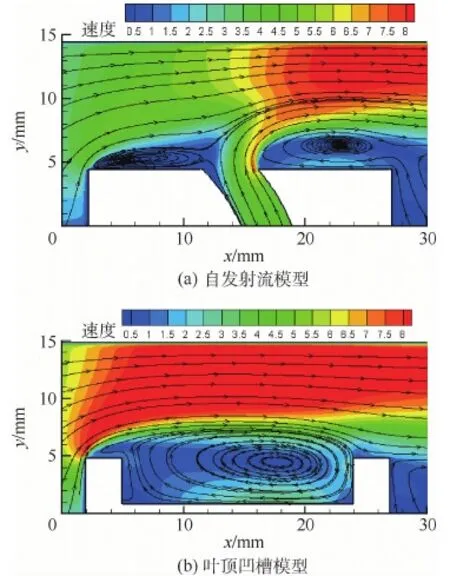
图9 自发射流与叶顶凹槽模型的叶顶间隙流场分布Fig.9 Tip clearance flowfield distribution of STI and tip groove model

PIV受到技术手段的限制(界面反光问题)，无法获得近壁区的流场细节，数值计算结果则提供了有益的补充。观察纯自发射流模型的计算结果可知，在自发射流的上冲作用下，间隙进口的分离泡变得非常显著。同时，由于自发射流本身具备一定的出流动能，泄漏流不能将其完全压制在叶尖表面，因此自发射流下游出现大范围的分离涡(Separation Vortex,SV)。2种效应共同导致泄漏流线被压缩，泄漏通道被挤占，因此产生了一定的泄漏抑制效果。

观察纯叶顶凹槽模型的计算结果可知，凹槽的引入本质是扩大流体动能的耗散，进而达到抑制泄漏流的目的。凹槽内流体在上掠流体(泄漏流)的非对称剪切作用和凹槽壁面的约束作用下必然形成流体旋涡，这带来两方面效应：①流体旋涡通过与壁面的摩擦和内摩擦，不断将流体动能耗散为热能，同时又不断从泄漏主流吸收能量维持这个旋涡，变相削弱了泄漏流动；②涡旋在凹槽内回流的过程中，受到压力边肋条的导向作用，向上冲击，压缩泄漏流线，挤占泄漏通道，表现出“膨胀涡”的特征，也可对泄漏流动产生抑制作用。

3.3 耦合方案的泄漏抑制机理分析

本节从流场分析角度探究3种耦合方案的泄漏抑制机理，揭示3种耦合方案在泄漏抑制效果上存在差别的原因。图10为进行比较的3种耦合方案，即凹槽压力边自发射流、凹槽吸力边自发射流及凹槽中间自发射流，分别命名为方案A、B、C。

观察图10(a)、(b)可知，方案A和方案B分别会产生2次有效的泄漏抑制过程，即自发射流的反吹阻滞和凹槽的旋涡耗散，其区别仅在于先后顺序不同。这2种耦合方案相对于纯叶顶凹槽模型的抑制能力均有所提升。其中，方案B的泄漏抑制效果优于方案A，其原因在于当自发射流出口位于吸力边时，自发射流进出口压差变大(接近压力面和吸力面压差)，因而可以获得高动量的叶尖射流，反吹阻滞效应有所增强，因而抑制效果更好。同时，由于叶顶凹槽的存在，在其下游区制造了一个动力阴影区，即为负压区，该效应进一步放大了自发射流进出口压差，强化了射流作用，加之凹槽涡本身的流体动能耗散作用，因此该耦合方案的泄漏抑制效果最好。

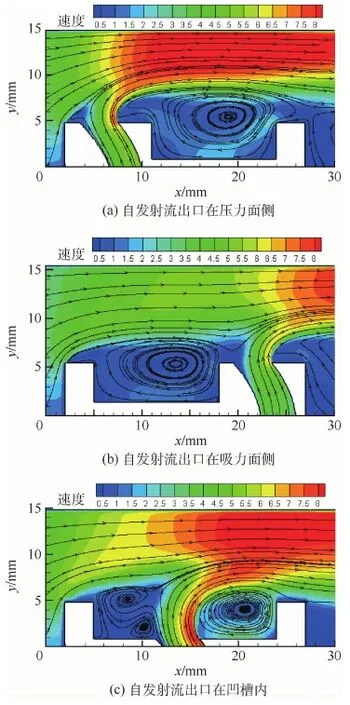
图10 3种耦合方案的间隙流场分布Fig.10 Flowfield of clearance for three coupled schemes

图8的计算结果表明，方案A的泄漏抑制效果不如纯自发射流模型。其原因在于当射流出口位于压力边时，自发射流的驱动力较小，因此无法获得高动量的反吹气流。同时，由于自发射流阻隔了凹槽涡和泄漏主流的直接接触，导致凹槽涡耗散的能量只能从自发射流中汲取，而不能耗散泄漏主流的动能，因此方案A的泄漏抑制效果较差。结果表明，耦合方案要获得好的泄漏抑制效果，需将2种被动抑制方法进行合理匹配。

图8的计算表明，方案C的泄漏抑制效果是最差的，甚至不如单一方法的泄漏抑制效果。观察图10(c)可知，当自发射流出口位于凹槽中部时，自发射流破坏了凹槽内旋涡，将原凹槽内的单个大尺度旋涡分割成若干小尺度旋涡。因为旋向的关系，射流上游形成2个旋向相反、强度较小的旋涡，射流下游形成一个强度较大的旋涡，这与试验测量的结果是一致的，再次验证了数值计算的正确性。自发射流上游的小尺度旋涡对泄漏主流动能耗散作用大为减弱，而下游高强度旋涡又无法直接跟泄漏接触，再者自发射流在破坏凹槽涡的同时，消耗了一部分动能，反吹阻滞效应被削弱。综合以上3方面效应，方案C的泄漏抑制能力被大大削弱。计算表明，相对于纯叶顶凹槽模型，凹槽中间射流叶型的泄漏抑制效果反而降低了4.79%。

3.4 耦合方案的间隙出口流速分布规律

不管是单一抑制方法还是耦合方案的泄漏抑制效果，最终都体现在间隙出口的流量变化上。因此，本节对比研究了5种模型的间隙出口流速分布，取间隙出口截面与流场中心对称面的交线为出口截面线(如图11左上角所示)，将截面线上的数据点绘制曲线，如图11所示。横坐标定义为无量纲距离θ，为数据点距离叶顶的垂直距离与间隙高度之比；纵坐标定义为无量纲流速ω，为数据点流速与间隙平均流速之比，通过图11可反映不同叶型间隙出口速度沿垂直方向变化情况。

观察图11可知，曲线大致可分为2种类型：第1类为凹槽中间自发射流模型和纯叶顶凹槽模型，其速度分布曲线变化特征为沿叶高方向，速度先单调上升，然后增速逐渐放缓，最后在机匣近壁区减速。图8的计算结果表明，这类叶型属于泄漏抑制效果较差的叶型。第2类为自发射流模型、凹槽压力边自发射流叶型和凹槽吸力边自发射流叶型，它们的速度分布特征为沿叶高方向，在近叶顶区域先有一个减速过程，然后才是增速过程、增速趋缓过程及近壁减速过程。图8的计算结果表明，恰好是叶顶附近有减速区的叶型是对泄漏抑制较好的叶型，且减速区延续越长，对泄漏的抑制能力越强，如凹槽吸力边自发射流叶型。以上研究表明，不同方案的泄漏抑制效果确实与不同方案下的叶顶间隙出口速度分布特征相关联。