基于TOPSIS方法的居民区电动汽车有序充电策略

师瑞峰, 梁子航, 马 源

(1. 华北电力大学控制与计算机工程学院, 北京市 102206; 2. 国网北京市电力公司昌平供电公司, 北京市 102200)

0 引言

近年来,中国超大城市电动汽车产业在购车补贴与车辆限行等多重政策激励下取得了飞速发展[1]。以北京市为例,政府通过购车指标控制、出行限号等措施鼓励和引导居民购买、使用电动汽车,致使电动汽车保有量呈现井喷式增长[2]。同时,充电设施建设与电网配套则呈现发展滞后、难以满足需求增长的态势,老旧居民小区由于早先设计的配电变压器总功率限制,大量电动汽车无法同时接入充电,因此,对合理的有序充电策略开展研究是保证小区正常用电、满足充电需求亟待解决的问题。

作为小区物业管理公司或充电桩管理企业,为避免变压器过载,需要精细控制同时运行的充电桩数量。传统先到先充(early come early charge,ECEC)策略可能导致部分早出晚归、通勤距离远的车主由于无法优先补电而影响次日出行;若用户都选择刚刚进入谷时电价阶段开始充电,则可能导致小区负荷激增,进而引发变压器过载。

现有相关研究主要集中在以下3个方面:第1类是基于小区基础负荷的有序充电策略研究,这类研究以居民区基础负荷为约束条件,通过充电负荷平移、网格法、最佳充电初始时间选择等有序充电策略实现削峰填谷的目的[3-5];第2类是电动汽车充电需求侧管理研究,这类研究通过模拟和预测电动汽车出行行为,获取充电需求,再进行有序充电管理,实现电动汽车用户充电经济性最优的充电策略[6-11];第3类是基础负荷与需求侧管理相结合的研究,这类研究在保证小区负荷不超限情况下,借助仿真分析工作实现充电成本与削峰填谷目标的协同优化[12-15]。

综上可以看出,现有有序充电策略研究主要考虑用户充电成本与充电负荷削峰填谷两类因素,在相同计费模式下,单位时间充电费用相等,总充电成本下降意味着充电时间和充电量的减少,避开峰时充电策略在降低成本的同时牺牲了充电时长。理想决策方案应同时优化这两类目标,获取目标折中的满意解。

本文从居民区电动汽车充电管理物业公司角度出发,在分析电动汽车充电需求基础上,构建了电动汽车运行、居民区充电的仿真系统;提出基于理想解法(technique for order preference by similarity to ideal solution,TOPSIS)的有序充电决策模型;以北京市某小区为例开展仿真研究,对仅在谷时充电、谷时—平时充电及不分时段充电等策略下,用户充电费用、平均等待时间、充电完成率、小区总负荷波动等指标进行分析,并与现有网格法所得结果进行对比,验证本文方法的优越性。通过对本文方法决策偏好权重的灵敏度分析,揭示不同决策偏好对充电方案的影响。

1 有序充电模型

1.1 问题描述

假设居民区每辆电动汽车停车位上均配有充电桩,当充电车辆过多时,由于小区配电变压器容量限制,部分电动汽车需要排序等待充电。

本文研究居民区电动汽车等待充电的排队规则,通过综合考虑相关因素,在满足用户充电需求和小区正常供电之间寻求平衡,实现用户充电成本、充电等待时间、充电完成率、小区负荷平均波动等多目标折中优化。本文决策优化模型如式(1)至式(8)所示。

优化目标:

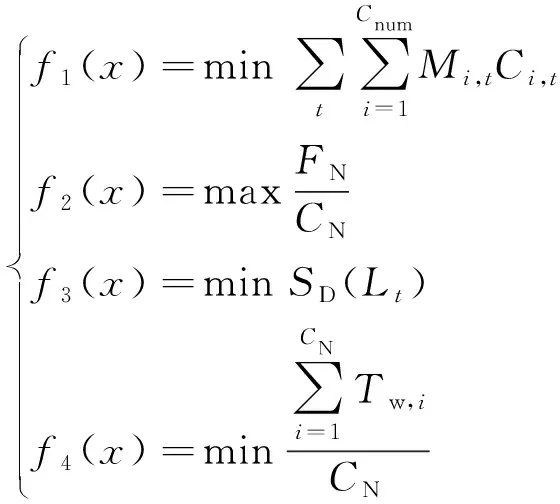
(1)

约束条件:

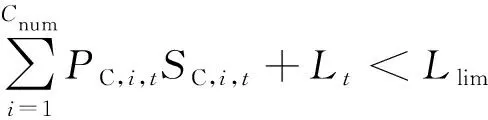
(2)

Ci,t=0,1

(3)

SC,i,t=0,1

(4)

Wi,t=0,1

(5)

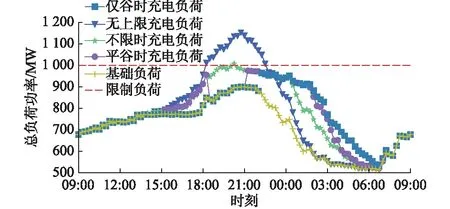
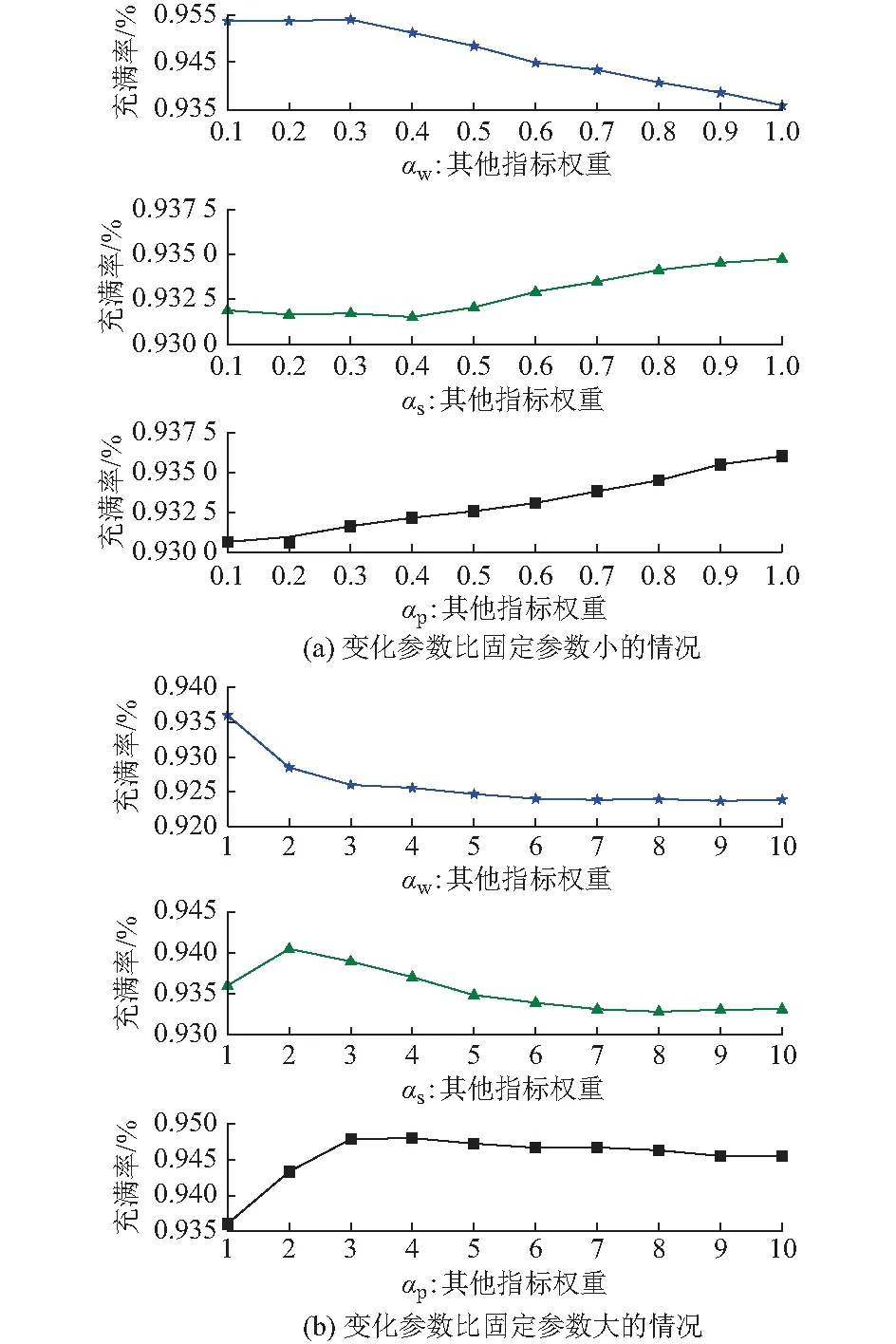
0

(6)

Ci,t=SC,i,t

(7)

Ci,t≤Wi,t

(8)

式中:f1(x)为充电服务费用;Mi,t为电动汽车i在t时刻的充电价格与服务费;Ci,t为t时刻电动汽车i的充电状态,若正在充电为1,否则为0;Cnum为系统内电动汽车总数量;f2(x)为充电需求满足率;FN为系统中充电车辆满意度大于90%的充电统计次数;CN为系统内所有电动汽车发生充电行为的总次数;f3(x)为居民区功率负荷平稳度;SD(Lt)为居民区负荷的标准差[16];Lt为t时刻居民区的功率负荷;f4(x)为用户平均等待时间;Tw,i为电动汽车单次充电时间;PC,i,t为第i个充电桩t时刻的充电功率;SC,i,t为第i个充电桩t时刻的充电状态,正在充电为1,否则为0;Llim为小区功率负荷上限;Wi,t为电动汽车i在t时刻的位置状态,在居民区内为1,外出为0;SOC,i为电动汽车i的剩余电量。式(7)表示电动汽车充电状态与对应充电桩状态一致;式(8)表示电动汽车充电状态受其位置状态约束,只有在回到小区内才有可能表现为充电状态。

第j次充电的满意度RP,j和FN的计算公式为[15]:

(9)

(10)

(11)

式中:Ereal,j为第j次充电的实际充电量;CEV,j为电动汽车第j次充电时的有效电池容量;Qexp,j为期望充电百分比;QSOC,j为充电初始电量百分比;fn,j为第j次充电的满意统计次数。

1.2 电动汽车出行及回程时间分布模型

根据2016年北京市交通发展年报的统计数据,北京市2016年小汽车出行时间分布如图1所示[17]。

图1 北京市小汽车出行时间分布Fig.1 Travel time distribution of vehicles in Beijing

早高峰出行时间集中在08:00前后,晚高峰回程时间集中在17:30—19:30。文献[18]通过正态分布拟合了全美家用汽车的出行时间分布规律。假设北京市小汽车出行时间服从正态分布,正态分布最高点计算方法如式(12)所示。

(12)

因此,由统计图拟合可得出电动汽车出行时间分布模型参数为:μ1=8,σ1=1.33;同理可得电动汽车回程时间分布模型参数为:μ2=18.5,σ2=1.99。结合北京市2016年小汽车年平均出行距离12 566 km[17],得出每天平均行驶34.42 km。考虑到交通拥堵造成的里程数波动,近似选取电动汽车出行距离为:平均距离35 km为中值、半径为15 km的均匀分布,其分布函数如式(13)所示,其中最大出行距离Dmax设为50 km,最小出行距离Dmin设为20 km。

(13)

根据北京市电动汽车普及率较高的北汽和比亚迪品牌车辆性能,设定电动汽车续航里程为200 km,电池电量采用慢充方式从零至充满时间为8 h。

1.3 居民小区模型

假设某老旧小区的变压器总额定功率为1 000 kW,住户数量150户,每户有一辆汽车。假设电动汽车渗透率为40%,则该小区的电动汽车数量为60辆,且每辆电动汽车的停车位都配有充电桩,即60辆电动汽车对应60个充电桩。根据相关研究方法,采用蒙特卡洛方法可模拟得到居民小区常规负荷曲线[3,4,12,19]。

电动汽车信息及行程计划由电动汽车出行分布模型及回程分布模型获得,其中出行及回程概率模型如式(14)、式(15)所示。

出行分布密度函数为:

(14)

回程分布概率密度函数为:

(15)

式中:出行分布参数为μ1=8,σ1=1.33,回程分布参数为μ2=18.5,σ2=1.99。是否外出则随机产生,并假设居民总出行概率为0.8。

2 基于TOPSIS方法的电动汽车有序充电算法

2.1 居民区电动汽车有序充电的TOPSIS方法

TOPSIS方法是一种典型的多目标决策方法,它具有简单、灵活、决策效果合理的特点。通过数据预处理技术对不同决策方案对应的属性进行去量纲、归一化并引入偏好,然后计算每个决策方案距离“理想解”与“负理想解”的相对距离后确定其充电排序的优先次序,实现各个决策属性与偏好结果共同确定最终排序方案的目标[20]。本文将TOPSIS方法引入居民区电动汽车有序排队充电问题,通过充电价格调整急需充电或等待时间较长的车主充电排序,在实现保证小区用电总负荷安全的前提下,尽可能提升电动汽车用户充电需求的整体满意度的目标。

本文电动汽车有序充电决策属性包括:用户充电平均等待时间(最小化)、用户充电成本(最小化)、用户充电完成率(最大化)、小区总负荷变化率(最小化)。通过分析不同决策属性偏好下的排序方案性能,可以获得符合决策偏好的综合满意有序充电方案。

2.2 算法流程

本文设计的电动汽车有序充电算法步骤如下(流程图见附录A图A1)。

步骤1:基础数据初始化。包括居民小区日常用电负荷,电动汽车数量及充电桩数量,电动汽车信息(包括慢充时间、电池容量、续航里程),电动汽车行程计划(包括是否外出、外出时间、归来时间、次日外出时间),仿真步长和仿真时间,以及电价策略等初始参数的设定。

步骤2:判断仿真是否结束,若仿真时间达到终止时间,则跳转步骤6;若还未达到终止时间,则判断当天仿真是否结束,若结束,则仿真时钟置0,仿真日期+1,若当天仿真未结束,则更新充电桩的可用数量信息。充电桩可用数量更新策略:先计算当前时刻满足居民小区总需求负荷外的可用功率,再估算该可用功率下的可工作充电桩数量(可用功率除以单个充电桩的额定功率)。

步骤3:对系统中的每辆车进行状态扫描,首先判断电动汽车所在位置,若不在小区内,则将其充电时间和等待时间置0,更新剩余电量,同时TOPSIS参数置0;若在小区内,则判断其是否需要充电,不需充电的车辆TOPSIS参数置0,需要充电的车辆,则根据其等待或充电状态更新其等待时间或充电时间、充电金额及剩余电量,若充满电则停止充电并将其TOPSIS参数置0。

步骤4:对电动汽车状态参数矩阵进行TOPSIS排序计算,计算当前时刻电动汽车的充电排序。

步骤5:根据排序结果更新电动汽车的充电及排队状态,仿真时钟增加15 min,转至步骤2。

步骤6:仿真结束后,统计电动汽车的时间序列信息,包括充电金额、等待时间、充电完成时间,以及居民小区负荷变化情况,包括平均功率、功率最大差值、功率标准差。输出仿真结果,仿真结束。

3 算例仿真

3.1 算例描述

本文以北京市某居民小区为例,在小区配电变压器总功率上限约束下,计算每一仿真时刻的可用充电桩数量,并选取电动汽车用户等待时间、停留时间及初始剩余电量为决策属性,通过TOPSIS方法计算满足决策偏好的有序充电方案,验证本文方法的有效性。

3.2 仿真实验设计

本文仿真模型对以下3类场景进行分析。

场景1:考虑无充电限制或引导的管理策略,即在电价的峰、平、谷时阶段均可充电。

场景2:考虑避开电价峰时的充电策略,即在电价峰时,所有充电桩均不工作,电动汽车在电价平时和谷时阶段按照有序充电规则排队充电。

场景3:考虑仅利用电价谷时充电策略,即电动汽车仅在电价谷时阶段按照有序充电规则排队充电。

在每种情景下,分别对比ECEC和基于TOPSIS排序两种排序策略所得方案的优劣。

3.3 参数设置

根据国网北京市电力公司有关规定设定公共充电桩的峰谷充电电价(见附录B表B1),所有时段的充电服务费均为0.8元/(kW·h)[21]。仿真时长设置为一个月,仿真步长为15 min;居民区模型的居民区负荷上限设置为1 000 kW;电动汽车数量及充电桩数量均为60;充电桩的额定功率为7 kW;电动汽车出行分布服从N(8,1.33);电动汽车回程分布服从N(18.5,1.99);出行概率为80%;出行距离服从U(20,50);慢充速率为0.125/h。

3.4 仿真结果分析

为分析不同时段充电排序策略对居民区电动汽车充电的影响,分别对不限时段充电、平时谷时充电和仅限谷时充电3种充电策略的TOPSIS方法排序与ECEC排序(共6种情况)进行仿真对比。

首先,考虑理想充电场景,即不设功率限制,用户随到随充;其次,考虑不限时段充电场景,即在不超越小区负荷上限的情况下,电动汽车可随时接入充电;然后,考虑在电价峰时避免充电,在电价平时和谷时根据小区剩余可用负荷分配充电的情形;最后,考虑仅在电价谷时(即当日23:00—次日07:00时段)根据小区剩余可用负荷进行充电的情形。

以某小区30 d居民用电及充电负荷跟踪为例,选取仿真时间内某一日的用电负荷仿真结果,结果对比如图2所示。

图2 不同充电策略的小区负荷对比Fig.2 Load comparison with different charging strategies in residential areas

从图2可以看出,如不对充电行为进行限制,小区傍晚用电高峰会与通勤归来的电动汽车充电高峰时段叠加,极大地增加了小区用电负荷峰值(如图2中无上限充电模式的用电总功率越限约15%),由此可能引发小区居民用电的电能质量下降甚至引发停电事故。图2中不限时段充电、平时和谷时充电、仅在谷时充电3种模式的TOPSIS权重向量设定为[0.25,0.25,0.5]。

从仿真结果可以看出,在不分时段充电情况下,同样会产生居民用电高峰与充电高峰的叠加,其充电费用、充电需求满足率、平均出行电量及标准差与不分时段ECEC结果类似,但最大峰值负荷保持在额定功率上限,不会引发电能质量明显下降或停电事故的情况;将时段策略改为在电价平时及谷时充电,可以将部分在18:00—21:00高峰时段的充电负荷后移至21:00之后的平时、谷时阶段,显著降低充电费用、改善居民用电负荷波动;最后,将电动汽车充电负荷后推至23:00谷时电价阶段后,即仅在电价谷时充电的策略,进一步改善平滑了小区居民负荷的峰值、增强了小区居民供电系统的安全裕度。

上述3种有序充电策略的TOPSIS排序与ECEC排序策略的仿真结果比较如表1所示。

表1 基于TOPSIS排序和ECEC排序结果比较Table 1 Sorting results comparison between charging strategies of TOPSIS method and ECEC

从表1的对比可以看出,相同充电策略下,电动汽车的单位时间充电成本相同,因此,充电金额高意味着电动汽车可获得更多电量;TOPSIS方法与ECEC排序策略获得的充电金额相差不大,但可以获得更高的充电完成率;衡量小区负荷稳定性的负荷标准差越小,代表小区负荷越平稳,TOPSIS方法较ECEC策略获得排序方案的负荷平稳性也有明显改善;此外,两种排序策略获得的充电平均等待时间也近似一致。因此,在相同充电策略下,TOPSIS方法排序结果要优于ECEC的排序结果。值得注意的是,采用谷时充电策略将充电时段后移会导致居民充电的平均等待时间延长(约为3.7 h),但由于夜间居民出行需求非常少,因此这种情况对使用需求的影响可以忽略。如果进一步实现自动值班更换充电桩(车)的系统,则可以完全忽略这种等待时长增加带来的用户体验劣化。

综合考虑各优化目标,仅在谷时充电的TOPSIS排序充电方法在充电成本和小区负荷稳定性两个目标上均取得了最佳效果,充电完成率也达90%以上。为避免充电结果无法满足用户用车需求的情况,可在用户排队进入充电等待系统时通过一定的方式告知用户其充电排序及其后各时段内车辆的预计充电量,以便用户灵活调节行程安排,因此该策略对改善居民区用电负荷特性、增强电动汽车充电服务能力发挥了积极作用。

3.5 仿真结果比较

为进一步验证本文方法的有效性,选取网格法(grid picking method,GPM)进行对比[4]。网格法与本文方法设计思想的差异如下:网格法在保证配电变压器功率不超限前提下,采用网格方式计算变压器的冗余功率(可接入负荷),并采用遗传算法寻求最佳实时可用的充电分配策略;而本文方法考虑仅在谷时、平时和谷时、不限时段3种场景下,采用TOPSIS方法选择同时考虑充电成本、充电需求满意率、小区负荷稳定程度(负荷标准差)多个决策目标时的最佳充电策略。

采用两种方法对同一电动汽车出行数据及居民区用电基础负荷数据进行仿真,在采用仅在谷时充电的时段策略下,对比电动汽车充电满意率及居民区负荷波动两个指标。为了突出对比效果,分别将小区电动汽车数量设置为60辆和80辆,TOPSIS排序方法的权重设置为[0.25,0.25,0.5],假设用户的充电期望都为100%,通过30 d的仿真,对比结果如表2所示。

表2 GPM与TOPSIS排序法对比结果Table 2 Sorting results comparison between GPM and TOPSIS method

从表中可以看出,本文方法在充电完成率指标上优于GPM;而GPM在小区负荷稳定程度指标上略优于本文方法,但这种稳定度的获取代价是GPM确定充电策略时,同一辆车的充电时间可能会被分配到几个分散时段。这种方式尽管对电网侧的负荷控制具备一定优势,但对于车辆电池性能衰减和寿命折损具有非常不利的影响,而电动汽车的电池价格大约占电动汽车售价的一半,电动汽车用户很可能并不会同意选择这种频繁充电的有序充电策略,因此其实际应用的可行性明显劣于本文方法。TOPSIS有序充电方法在保证充电满意率的情况下,对符合充电优先级别的电动汽车进行连续充电,这种有序充电策略对居民区管理者及电动汽车车主都有一定的吸引力,因此可以认为TOPSIS排序方法在居民区电动汽车有序充电中有效且可行。

3.6 TOPSIS权重灵敏度分析

为了进一步考察TOPSIS方法权重设置的合理性,本节通过控制变量法进行分析,将等待时间参数的权重设为aw,停留时间参数的权重设为as,剩余电量参数权重设为ap。

首先,采用仿真效果最好的仅在谷时充电的TOPSIS排序方法。为了使得实验结果更明显,将模型中电动汽车的数量增加到80辆,假设每辆车的预期充电量都为100%,最终电量充到100%记为一次满意,选取充电满意率和居民小区负荷标准差两个指标作为对比值。

接着,设置TOPSIS方法的权重。先测试等待时间参数的权重,令停留时间参数的权重与剩余电量参数的权重相等,即as=ap,aw与as和ap的比值如式(16)和式(17)所示。

(16)

(17)

同理,采用相同的方法对可充电时间和剩余电量参数进行分析,对每个不同权重下的电动汽车充电满意率及居民区总负荷标准差指标进行仿真和对比。取10次不同初始数据集仿真下指标的平均值进行对比,充满率随权重系数变化如图3所示。

图3 权重变化对充满率的影响Fig.3 Impact of weight change on charging satisfaction

由图3可见,等待时间参数权重占比越小,充电满意率越高,当αw大于另外两个参数的权重时,满意率基本稳定;当αs比另外两个参数权重稍大时,满意率出现一个高峰,继续增大αs则会降低满意率;而αp占的比例越大,充电满意率越高,在比例为5倍时达到最大值,符合现实规律。

因此,充电满意率指标与小区负荷标准差指标为两个互斥的指标,本文仿真采用的权重值为[0.25,0.25,0.5],更多考虑的是电动汽车用户充电的满意程度。作为居民区停车场运营管理方,可以根据实际需要调整TOPSIS排序方法的权重,使居民区有序充电更符合预期。

4 结语

老旧居民区由于早先设计时的变压器负荷容限低,难以适应电动汽车迅猛增长的充电需求。本文提出基于TOPSIS方法的居民区电动汽车有序充电策略,在兼顾用户充电成本、充电完成率、充电等待时间的基础上,提高了小区居民用电总负荷平稳性。通过仿真研究对比了各种充电策略下基于TOPSIS方法与ECEC策略、GPM等方法的排序方案。结果表明,本文方法相对纯粹的谷时充电策略或GPM充电方案,可以在相似的经济性前提下有效提高用户充电的满意率、降低小区总负荷峰值,并增加小区负荷平稳性。

由于本文研究仅考虑了3个与充电完成率关系密切的属性作为TOPSIS方法排序的参考依据,未能考察其他可能影响充电排序的因素,在今后研究中应进一步全面考虑各种可能影响决策方案的其他属性,增强方法的实用性,为相关部门解决好居民区电动汽车有序充电难题做好决策支撑。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。