基于高斯-牛顿法的水下导航系统校准算法研究

吴媛媛 张 森 郭锦标

（1.中国人民解放军31003部队 北京 100089）（2.海军工程大学 武汉 430033）

1 引言

随着国家发展战略对海洋的开发和利用的需求不断提升，对水下导航定位系统的要求也越来越高：低成本、使用和布放回收方便、允许任意数量接入的用户等［1～3］。基于单个信标的水下导航系统因其成本低、布放回收方便等优点在海洋的开发和利用中越来越受到关注，因此研究价值也越来越高［4］。

多正交信号水下导航系统［5］通过一个信标同时发射一组正交信号，使得接收端接收到信号就可以解算自身的位置，系统由水下的声学设备和船上的信号处理设备及GPS等组成，如图1所示。

由于在布放信标时，信标的精确位置不得而知，并且信标会出现一定的倾斜，接收端需要获知信标的精确位置和倾斜数据，以此修正解算值。信标的位置信息和倾角信息是导航系统位置解算的必须数据，因此通过校准获得信标的地理坐标和偏角是多正交信号水下导航系统的一项关键技术。

国内最早由唐秋华等［6］提出超短基线定位系统的校准算法，它是将安装校准的三个旋转角度偏差和三个位移偏差等效作参数估计问题，在最小二乘准则下估计各个量的值，并对其进行优化。哈尔滨工程大学的杨国保［7］将声线弯曲、校准航迹作为影响校准稳健性的因素，提出了改进的估计方法和数值解法，提高了校准的稳健性。多正交信号水下导航系统是由海军工程大学水声技术研究所张森团队首次提出，关于该系统的校准算法目前还未有专门文献记载研究。本文借鉴超短基线声学定位系统的校准算法思想［6，8］，提出了最小二乘准则下基于高斯-牛顿法的多正交信号水下导航系统的校准算法。

2 信标的位置估计

信标投掷于水下时概略地记录下投入点的地理坐标，信标源与接收端之间看成是两点之间的直线距离。船绕着信标航行，在每个测量点上通过水听器接收信号，获得时延信息，用声学方法可以测量出信标源与接收端的距离。应用空间测距交会的原理，可以求解出水下信标在大地坐标系下的坐标( )

X,Y,Z。

在得到每个观测点与信标的距离后，应用基于高斯-牛顿法的最小二乘原理［9］计算出信标的坐标位置，具体计算方法如下：

1）应用空间定位的测距交会原理列出观测方程为

其中，X,Y,Z为待求的水下信标在大地坐标系下的坐标，Xi、Yi、Zi(i =0,1,…n)为接收端（水听器）在大地坐标系的坐标（n为船测量的次数），Si为利用声学方法测出的信标与水听器的距离。

2）利用一阶泰勒公式展开原理就可由观测方程列出误差方程

将式（1）在初值处线性化后可以得到下式：

式中，X0,Y0,Z0为水下信标在大地坐标系下的概略坐标值。

3）根据最小二乘原理求解

求未知参数Xˆ的最小二乘估计，就是寻求Xˆ的一个估值，使：

其中P为观测值的权矩阵，一般都认为是等权观测，即P为单位矩阵。为此将式（5）对 Xˆ求一阶导数并令其为零，得到：

将式（4）代入到式（6）得到：

则可以得到：

求得Xˆ后则可以根据：

通过迭代计算得使得改正值达到规定的误差限，即可得到水下信标的精确地理坐标。

3 信标的姿态估计

在得到信标的大地坐标后，根据基阵坐标系与大地坐标系之间的转换关系［10］，可以得到：

其中A为方位角、κ为纵摇角、φ为横摇角。为方便表示，令

利用最小二乘法计算三个偏角的具体方法如下：

（1）对式（11）利用多元函数的泰勒公式展开，并取其一次项［11］，即

式中X0,Y0,Z0为多元函数的初始值，将上式写成误差方程式为

式中，x',y',z'为基阵坐标系在初始的旋转角度A0,κ0,φ0（可以假设为零）求得。

（2）假设需要求解的三个参数 A,κ,φ都是在较小值的情况下，则式（15）在 A,κ,φ均用零为近似值代入，则：

（3）将误差方程式（17）表示成矩阵的形式为

经过N次测量，则可列N个误差方程，写成矩阵形式则可以表示为

根据最小二乘法原理，可求得误差方程式的解为

将已知的参数代入方程式，即可求出初始旋转角度的改正值Δφ,Δκ,ΔA，将其加到初始值上得到新的近似值：

将得到的近似值再次作为初始值，重新建立新的误差方程式，再次求解改正值，直到各个改正值小于规定的限差值为止。

4 校准算法仿真分析

4.1 航迹的仿真

仿真实验假定船的航行轨迹为“⊕”，在圆周和两条相交直径上取均匀的观察点，以船的航行轨迹圆的圆心为坐标原点，海平面深度为0，向下为正，船的测量点的轨迹在水下信标位置周围绕行，如图2所示。

4.2 信标的位置估计

假定实际信标位置的大地坐标为（50，100，500），规定算法的误差限为1m 。研究GPS测量误差和接收端时延误差对估计的影响。

GPS存在测量误差，接收端的时延测量也会产生随机误差，且这些随机误差服从均值为零的高斯分布［12］。从图3（a）可以看出位置估计误差大小与GPS测量误差成正比；接收端的时延误差使得信标与水听器的距离发生偏差。同样位置估计误差大小与距离误差成正比，如图3（b）所示。

4.3 信标的姿态估计

观察算法在不同偏角下的估计结果，并将得到的估计结果解算得到船的地理坐标，GPS测量误差1m，接收端的时延误差1μs，得到在水平方向定位误差的均方值，具体数据如表1所示。

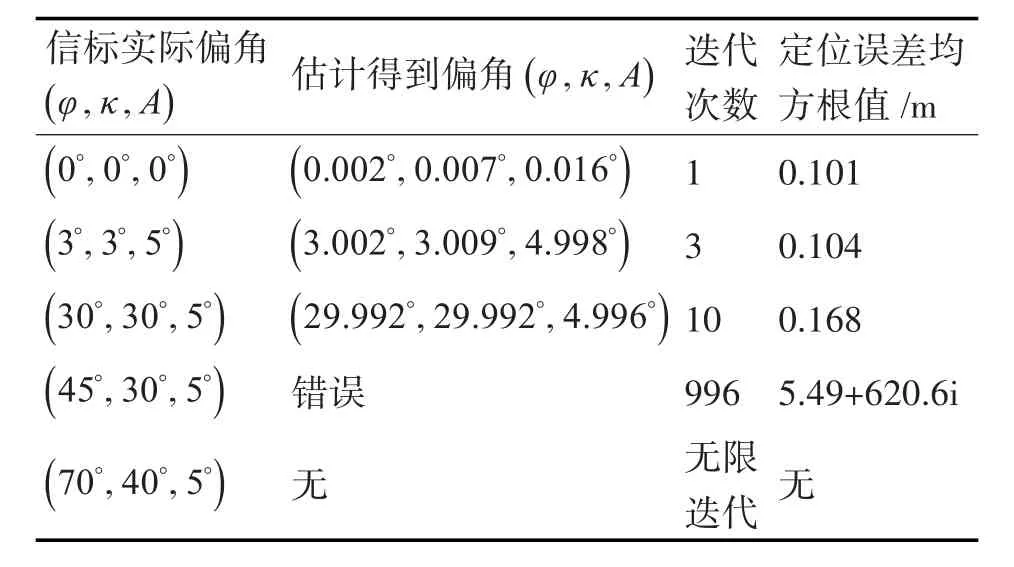
表1 姿态估计结果

5 结语

本文研究了基于高斯-牛顿法的多正交信号水下导航系统的校准算法，通过仿真分析可以得到以下结论：

1）位置估计对初值的依赖不敏感，估计的误差大小与GPS测量误差和时延测量误差大小成正比；

2）小角度的估计具有很强的稳健性，算法所需少次迭代次数，但是当水下信标偏角不是小角度时，此姿态估计算法不再适用。