Quench Dynamics of Neutral Atoms in Out-Equilibrium One-Dimensional Optical Lattices∗

V.Leyton, A.Argu¨elles,and M.Camargo

1Centro de Investigaci´on en Ciencias B´asicas,Universidad Santiago de Cali,Calle 5 No.62-00 Cali,Colombia

2Centro de Investigaciones en Ciencias B´asicas y Aplicadas,Universidad Antonio Nari˜no,Km 18 via Cali-Jamund´ı,760030 Santiago de Cali,Colombia

AbstractA quantum simulator is proposed for nucleation and growth dynamics using an out-of equilibrium optical lattice.We calculate the density of neutral atoms in the lattice and we establish the connection with the Kolmogorov-Mehl-Johnson-Avrami model.Here we show that an Avrami equation can describe most of the evolution in time of the population growth in the lattice,coherence between neutral atoms leads a complex growth rate.

Key words:1D optical lattice,Bose-Hubbard model,out-equilibrium system,nucleation

1 Introduction

Ultracold bosonicand fermionicquantum gases are versatile and robust systems for probing fundamental condensed matter physics problems like quantum phase transitions,[1−3]squeezed states in a Bose-Einstein condensate,[4−5]Tonks-Girardeau gas in a onedimensional lattice,[6−7]vortices and superfluidity,[8−10]as well as finding applications in quantum optics and quantum information processing like state selective production of molecules in optical lattices[11−12]and induced oscillations between an atomic and molecular quantum gas.[13−14]Storing such ultracold quantum gases in arti ficial periodic potentials of light has opened innovative manipulation and control possibilities,[15−16]in many cases creating structures far beyond those currently achievable in typical condensed-matter physics.Ultracold quantum gases in optical lattices can in fact be considered as quantum simulators for the study of real materials,[17]till the simulation of a Dirac field near an event horizon,[18]due to they offer remarkably clean access to a particular hamiltonian and thereby serve as a model system for testing fundamental theoretical concepts.

Storing interacting atoms in optical potentials are a very interesting setup.Despite the presence of interaction between atoms,which lead to nonlinear terms in the Schr¨odinger-like equation(Gross-Pitaevskii equation),[19]the macroscopic wavefunction still describes the quantum many-body system in the weakly interaction regime.If strong interacting regime with respect to the kinetic energy,the system in general can not longer be described as a simple matter wave.An example of the relevance of the interaction strength is the superfluid-to-Mott insulating state transition when the system go from a weakly interacting quantum system to a strongly correlated quantum many-body system system.[1]For weak interactions the system form a Bose-Einstein condensate of matter.The system tends to such state as the kinetic energy the kinetic energy is minimized for single particle wave function spread out throughout the lattice.For a strong interparticle interaction relative to the kinetic energy,the system reaches the strongly correlated state or a Mott insulator state,in which the atoms are localized to single lattice sites.There the system cannot be described by giant coherent matter wave,and no interference pattern can be observed upon releasing the particle from the lattice.

Mott insulators in one dimension have become attainable through the use of a deep two-dimensional optical lattice loaded with a Bose-Einstein condensate(BEC).[20−22]In that setup the condensate splits up into several thousand individual one-dimensional BECs in each of the potential tubes.Subsequently,a third lattice potential applied along the direction of the tubes can drive the transition to the Mott insulating state.Other possible mechanism to drive the system to the Mott insulating state is drive parametrically the tubes,[23]thus the on-site interaction can be tuned and a transition induced,by tuning the external modulation it can even mimic a Tonks-Girerdeau gas dynamics.Experiments where an ultracold quantum gas has been controlled by means of periodic external modulation has been realized,in which the ballistic spreading of a localized Bose-Einstein condensate in the lowest band has been almost suppressed by the application of an time periodic external force in a one-dimensional optical lattice.[24]In those experiments a one-dimensional lattice is created in the tight-binding regime along the x direction together with a tube-like harmonic confinement in transverse directions y and z.In that setup a Bose-Einstein condensate is loaded(like87Rb)in the lowest Bloch band of the lattice,localized in the center of the tube by additional trapping potential(along x).When this trap is removed the condensate expands along the tube,additionally a time periodic external force is applied shaking the lattice back and forth,for more details see Ref.[25]and references therein.

Recently the quench dynamics in Rydberg gases has been studied in the classical and quantum regimes.There the Kolmorov-Johnson-Mehl-Avrami(KJMA)frame work wasused foran analyticalunderstanding ofthe quench dynamics with the coupling with a dissipative environment.[26]Following their approach we consider in this work the quench dynamics of neutral atoms in a onedimensional system.We address to the nucleation problem when the lattice is built from an optical potential driven by an external field.

In the following we shall introduce the time dependent Hamiltonian and the rotating wave approximations.In Sec.2 we shall introduce the out-equilibrium set up use to study KJMA nucleation process in optical lattices.In Sec.3 we describe the quench protocol for the nucleation and growth in the quantum regime.After that,in Sec 4 we analyze the population of the lattice in terms in the KJMA framework and we discuss the difference with the classical setup.We conclude in Sec.5.

2 Modulated One-Dimensional Lattice

We consider a one-dimensional optical lattice along x direction created by a laser beam with the optical potential Vlattice(x)= −V0cos(2πx/a)/2+V0/2,with a as the lattice size and V0as the depth of the potential well.If the standing wave that constructs the optical lattice is generated by a directing a laser beam against a mirror,it is possible to modulate the position of the mirror periodically in time.[24]Thus,the optical potential become Vmod(x,t)=Vlattice(x+Acos(ωt)),with A as the amplitude and ω the frequency of the mirror modulation.For weak driving strengths characterized by A≪a the modulated optical potential around the minimum xn=na reads as

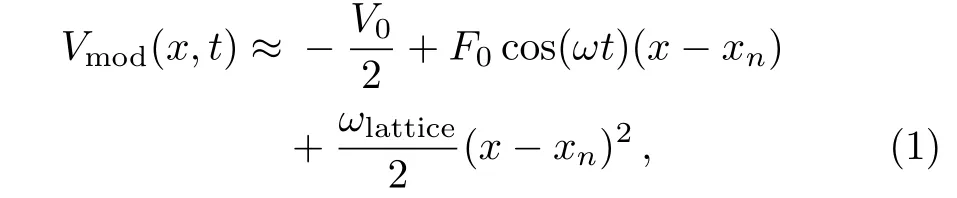
therein F0=2πV0A/a and ωlattice=V0(2π/a)2are the effective driving strength and the onsite proper frequency respectively.The resulting potential corresponds to the simple case of a driven harmonic potential around each minimum xn,it is common in the study of laser-atom interactions in the dipole approximation.

In the lattice frame of reference the system can be modeled by the Hamiltonian

It is convenient,for later purposes,switch to a frame of reference rotating under the angle θ(t) =ωt,by performing the canonical transformation R(t)=exp[−iθ(t)∑ nk].Here,we are interested on the quench dynamics of the lattice around twice its fundamental frequency,for ω ≈ ω0.We further assume a weak modulation regime,where≪ ω0.This allows us to invoke the rotating wave approximation,in which the fast oscillating terms will be negligible around fundamental frequency for weak enough driving.By eliminating all fast oscillating terms from the transform Hamiltonian,one obtains the following time-independent Hamiltonian

There,we have introduced the detuning frequency δω = ω − ω0.In the following we shall introduce the quench protocol and calculate the density of particles in the lattice with the time-dependent-block-decimation method using open source software from Carr Theoretical research group.[27]

3 Quench Dynamics

As an initial preparation we consider an empty lattice,in the regime under the condition U ≫ J where the tunneling process is not favorable and the coming particles will fill the lattice.In order to facilitate the filling process we set the detuning such that it cancels the interaction energy of adjacent filled sites,i.e.δω = −V,thus the Hamiltonian model becomes

In the hardcore regime the onsite interaction term(∝U)does not contribute to the dynamics.Opening a channel for the driving process opens also a channel for dissipation,this out-equilibrium dynamics is modeled by coupling the system to a bath composed by an infinite collection of harmonic oscillators named environment.For a weak system-environment coupling one can invoke the Born-Markov approximation leading to the Lindblad master equation[28]

where the second term models decays and decoherence processes,with a rate γ ≪ ω0.One can rewrite the above master master equation in an alternative way[29]

4 KJMA Framework

The KJMA theory is a standard stochastic of nucleation and growth,the model describes how liquids transform to solid at constant temperature.[30]This model describes the kinetics of crystallization,in general it can be applied to other changes of phase.This model predicts a smooth change of the order parameter that defi nes the phase like a compressed exponential formµ(t)=1− exp[−(Γt)2],the so-called Avrami equation for a 1D system,where Γ is the nucleation rate.Here µ is the fraction of occupied sites.The KJMA frame work allows to quantitatively understanding of the out-equilibrium dynamics introduced the previous section.

In general,we can expect the fraction µ follows[30−31]

where R(t)is the growth rate.For a lattice of L sites the quantum analog of the fractionµis equal to the density of particles,The effective nucleation ratecan be calculated from the density,and therefore the characteristics of the nucleation process.In the weak coupling regime to the environment the structure of the growth rate is not trivial.While the lattice is populated coherent processes becomes relevant until the number of neighbor particles is enough to destroy it.This effect is not observed from the density of particles,see Fig.1(a),but it is more evident from the behavior of the effective nucleation rate,see Fig.1(b).Once the lattice starts to be occupied from incoming particles the densityis well described by the Avrami equation,i.e.at the beginning the effective growth Γefft2,and Γ2R(t)t,see Figs.1(b)and 1(d).There we have delimited the region in the time evolution where the the system can be modeled by the Avrami equation.

Fig.1 (a)Time evolution of the particle density for a lattice of L=200 sites,interaction energy V=1,driving strength f=10−1V,and damping rate γ =5 × 10−2V.The time evolution of the effective nucleation rate is depicted in(b),where we have shadowed the region for Fe ff(t)∝t2,a quadratic fit of the points in that region is shown with a coefficient of determination R2=0.999.In(c)we show a sketch of the modulated optical lattice in one dimension.In(d)we calculate the behavior of the growth function,a linear fit is shown in Fig.1(a)with R2=0.999.The calculated effective nucleation rate Γe ff ≈ (0.03)2t2−0.3t+0.2 in panel(b)is used in panel(a)to plot the Avrami equation.

4.1 Moderated Driving Strength

For a moderated driving strength the effective rate Γeffexhibit a very rich behavior,since the modulation strength is not strong enough to drive the system to a classical regime,but it can induce coherent processes.In the first stage of the population process,see the shadowed regions in Fig.2,the nucleation rate Γ,which is proportional to the line curvature,is larger as stronger is the driving amplitude f.It is depicted in the particle density behavior in Fig.2(a),there the density approaches to its maximum value faster for higher values of the driving strength.The shallow regions in Fig.2 are limited by the linear behavior of the growth rate(see Fig.2(c)),before that region limit we expect the nucleation process is trivial and R∝t.After that region the particle density reaches the maximum value following a non-trivial growing law(R(t) ∝ t),this is very interesting since the driving strength is not strong enough for consider a classical regime(f≪V)but still strong to overcome dissipative effect from the external environment.

Fig.2 (a)Time evolution of the particle density for a lattice of L=200 sites for different values for the modulation strength in units of the interaction energy V=1.The damping rate used is γ =1×10−2V ≪ f.In addition the time evolution of the effective nucleation rate is depicted in(b).In panel(c)we show the behavior of the growth rate function.

5 Conclusions

We have considered the nucleation and growth process of neutral atoms in a one-dimensional out-equilibrium optical lattice.The lattice is driven out-of equilibrium by the an external modulation.The population in the lattice is described by the KJMA model,which explains crystallization processes in liquids and other classical setups.The model describes the population growth until coherence states emerges from the inter-particle interaction.The effective nucleation rate and the growth rate can be calculated from the particle density measurement.This allows to connect classical nucleation and growth with the quantum dynamics in optical lattices.As a perspective of this work could be the connection of the growth rate with the space and time correlation function in the number of particle in the lattice.