Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
2018-11-24TabassumMehmoodandMaraj
R.Tabassum,R.Mehmood,and E.N.Maraj
1Department of Mathematics,Faculty of Basic and Applied Sciences,Air University,Islamabad,Pakistan
2Department of Mathematics,Faculty of Natural Sciences,HITEC University,Taxila Cantt,Pakistan
AbstractThis communication addresses the impact of heat source/sink along with mixed convection on oblique flow of Casson fluid having variable viscosity.Similarity analysis has been utilized to model governing equations,which are simplified to set of nonlinear differential equations.Computational procedure of shooting algorithm along with 4th order Range-Kutta-Fehlberg scheme is opted to attain the velocity and temperature distributions.Impact of imperative parameters on Casson fluid flow,temperature,significant physical quantities such as skin friction,local heat flux and streamlines are displayed via graphs.
Key words:oblique stagnation point flow,variable viscosity,partial slip,mix convection,heat generation/absorption,Runge-Kutta Fehlberg scheme
1 Introduction
Stagnation point flows are the most common fluid flow studied and examined in field of fluid dynamics because of its frequent occurrence in many industrial and manufacturing procedures.The most general case for fluid striking on a solid rigid surface is when fluid strikes the surface at any random angle.Most of the research had been performed for the special case when fluid particles strike the surface orthogonally.In the field of aerodynamics,aeronautics and marine engineering problems oblique stagnation point flows are usually encountered.These flows have gained attention by many researchers and engineers during past few decades due to the above mentioned primary reasons.Stagnation point appears whenever a flow encroaches on a solid surface.For stagnated flows,the velocities approach to zero along with the highest pressure on the surface.[1]The boundary layer flow striking obliquely on a rigid plane has many engineering applications especially in aeronautics.These flows usually arise when a spurt of viscous fluid obliquely strikes on the rigid plane because of surface silhouette or physical constraints on nozzle.[2]In early twenties researchers have made good investigations in this context.Investigation on steady,nonorthogonal stagnation point flow was performed by Reza et al.[3]They reported the existence of boundary layer for the case where the surface stretched with velocity less than free stream fluid velocity.Moreover,upturned boundary layer appeared when a fluid far away from stretched surface flows with velocity less than stretching surface velocity.Li et al.[4]investigated forced convection influence on heat transfer of viscoelastic fluid transport towards an in finite planar surface.They found that viscoelasticity of thefluid contributed in decelerating fluid flow and momentum boundary layer thickness.Rahman et al.[5]explored such flow for nanofluid towards a shrinking surface.They concluded that thicknesses of momentum,thermal and nanoparticles volume fraction decreased with an increase in shrinking parameter,for the upper branch solution and reversed trend was noticed for the lower branch solution.Moreover,flow obliquity toward the surface is increased as strain rate intensifies.Influence of applied magnetic field along with thermal radiation on heat transfer phenomenon was examined by Lv and Zheng.[6]Notable findings included that velocity slip affects the fluid flow significantly.Shahmohamadi[7]employed Casson model for steady free convective boundary layer flow where wall temperature was taken variable on horizontal plate.Another investigation on Casson model was performed by Nadeem et al.[8]They considered hydro magnetic flow towards a nonlinearly shrinking porous planar sheet.Another innovation considering the Casson nanofluid was reported by Nadeem et al.[9]Ellahi et al.[10]derived homotopic analytical series solution of MHD third grade fluid in which the effects of variable viscosity were considered.They depicted that increase in pressure gradient decelerated fluid flow and third grade fluid parameter contributed in reducing temperature and velocity distributions.Elbashbeshy and Bazid[11]used Runge-Kutta numerical integration scheme to examine heat transfer towards an extending surface infl uenced by variable internal heat generation and viscosity having inverse linear relationship with temperature.Umavathi[12]applied a non-Darcy model to numerically investigate the combined effects of fluid thermo physical characteristics and variable viscosity on free convectiveflow.Lin et al.[13−15]considered a Marangoni boundary layer flow of nanoliquid containing copper nanoparticles over a permeable disk with MHD and different nanoparticles shapes effects.No slip condition between base fluid and nanoparticles was assumed.In some other investigations Lin et al.[16−17]studied the influence of film momentum,internal heat source and thermal transport characteristics of thin power law liquids upon a stretched surface placed horizontally with influence of viscous dissipation and variable thermal conductivity.Lin et al.[18]also examined the heat transport characteristics of nanofluid in a rotating circular groove.Two types of thermal conductivity models were considered.Recently Manjunatha et al.[19]carried out a numerical investigation on electrically conducting dusty fluid over an unsteady extending planar surface.In this problem both conductivity and viscosity were taken variable.Influence of slip condition on nanofluid transport towards an elongating sheet was inspected by Noghrehabadi et al.[20]Thermal radiation effects along with partial slip on a boundary layer flow was explored by Mukhopadhyay and Golra.[21]Das[22]incorporated variable internal heat source/sink,thermal buoyancy and partial slip in a convective heat transfer enhancement of nanofluid passing over the porous elongating surface.Gorder and Vajravelu[23]made a comparative analysis of analytical and numerical solution of convectiveflow towards a permeable stretching sheet.Suction and internal heat source/sink consequences were also taken into account.Alsaedi et al.[24]extended it by considering nanofluid with convective boundary condition.Coalesce outcomes of mixed convection and internal heat generation or absorption in lid-driven cavity under the influence of magnetic field was investigated by Kumar et al.[25]Recent contributions in this regard include Refs.[26–29].
In the light of above discussion,this is an attempt to examine influence of partial slip condition and heat generation/absorption on an oblique stagnation point flow in presence of mixed convection and variable viscosity.No such attempt has been reported in literature yet.Our formulation contains nine parameters,namely,slip parameter ω,heat generation constant δ,mix convection parameter λ,variable viscosity parameter α,Casson fluid parameter β,Prandtl number Pr,Biot number Bi,stretching ratio a/c,and obliqueness of flow γ.Influence of above mentioned parameters on velocity and temperature distribution in addition to significant measurements like skin friction,local heat flux and flow patterns are examined through graphs.Present novel finding may be beneficial and useful in academic research,aerodynamics and marine engineering.
2 Problem Development
Here we consider a non-orthogonal steady flow of a viscoelastic fluid towards the planar stretching sheet.Planar surface is place along x-axis.Surface is stretched in such a way that origin remains unaltered as shown in Fig.1.Physical flow problem is considered to be influenced by partial slip condition and mix convection in presence of heat source or sink.Moreover,viscous dissipative effect is ignored in present study.Furthermore,all the fluid physical characteristics are taken to be constant except viscosity.Model equations of the flow can be written as:[9]
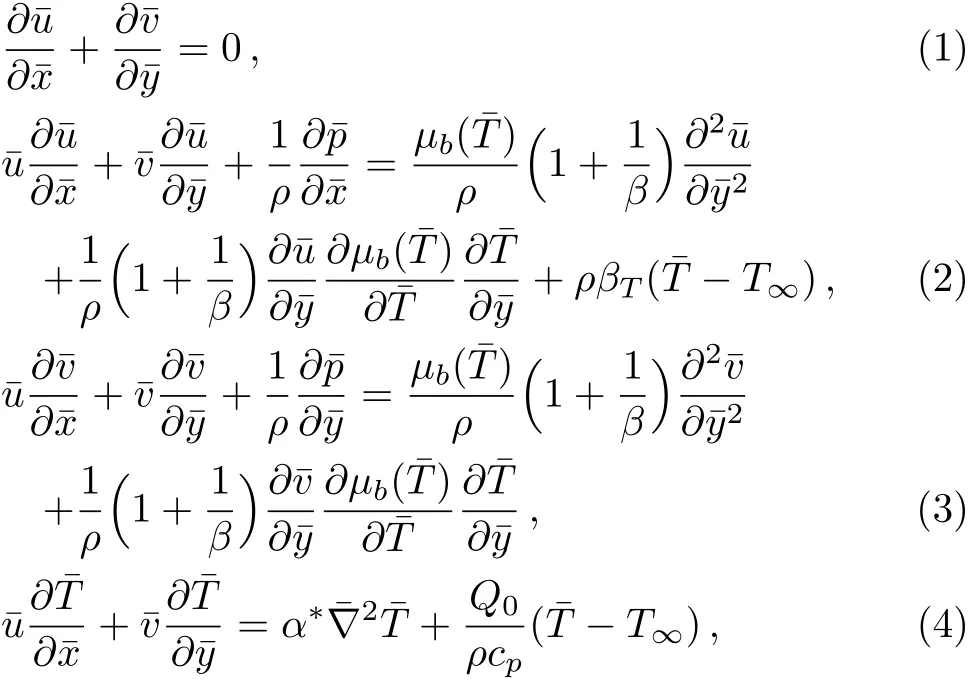

In which a,b,and c are dimensional constants and N is slip constant.

Fig.1 Description of the flow.
Utilizing similarity analysis and employing following relations as defined in Ref.[9]
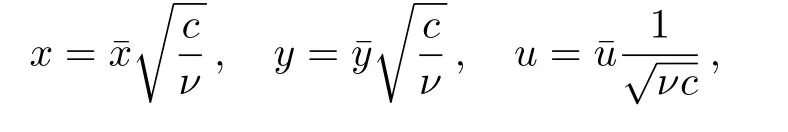
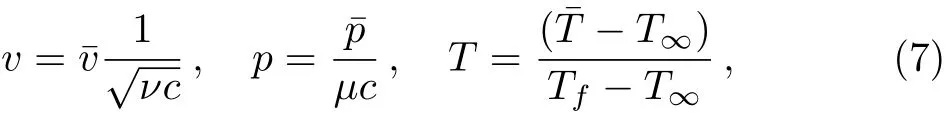
where ν is the effective kinematic viscosity. Invoking Eq.(7)into Eqs.(1)to(6),following non-dimensional form is attained
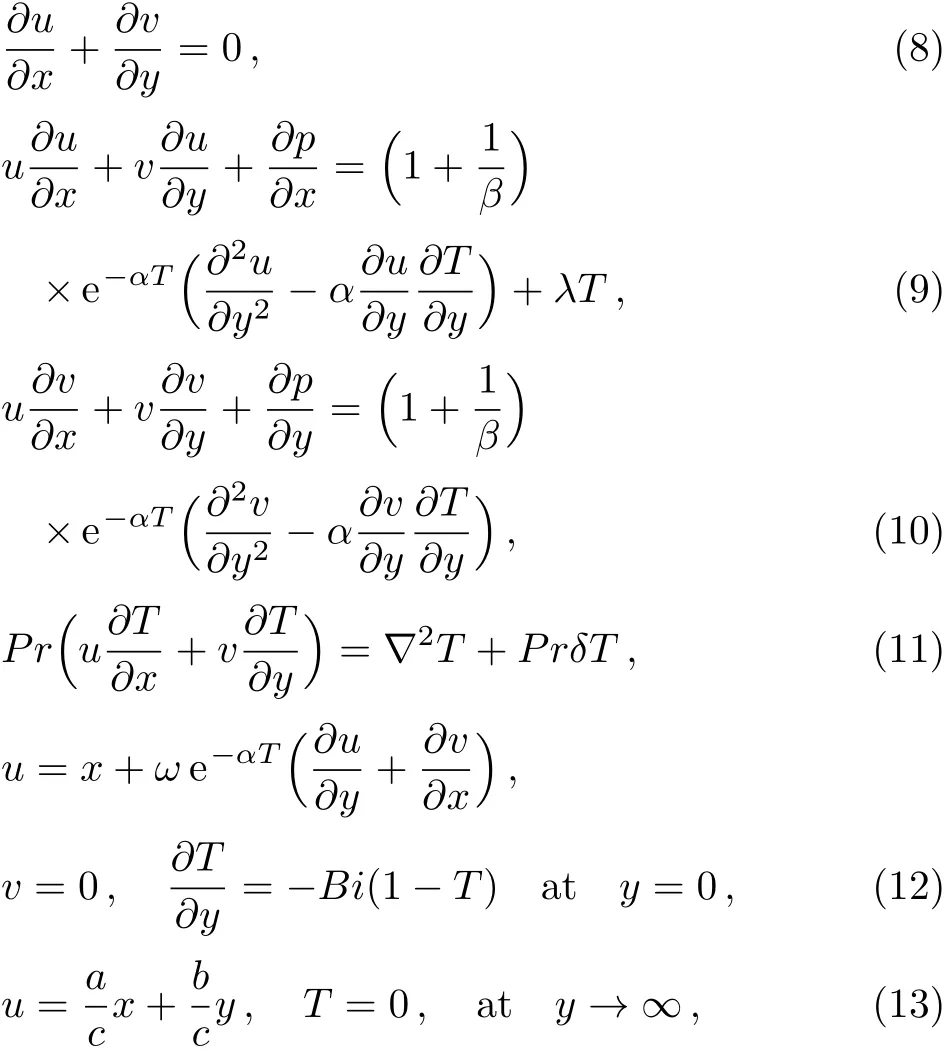
where α =d(Tf− T∞)represents variable viscosity parameter,γ=b/c characterizes obliqueness of the flow,is Biot number,Pr= ν/α is the Prandtl number,is the mix convection parameter,is the slip parameter and δ=Q0/cρcpis the heat source(δ>0)or sink(δ<0)parameter.By invoking well established stream function relations[9]

Incorporating above relations in Eqs.(8)to(11)and elimination of pressure term p by means of the equality pxy=pyxin Eqs.(9)and(10),gives

Following associated boundary conditions are yield:
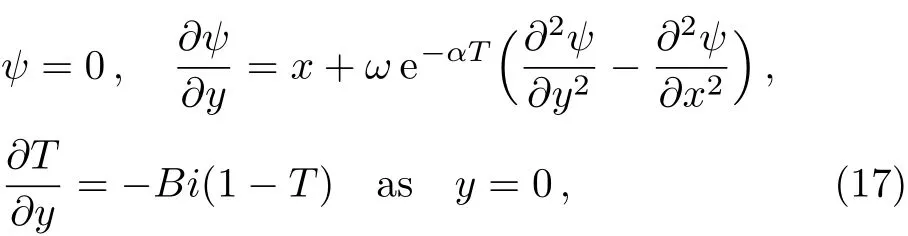
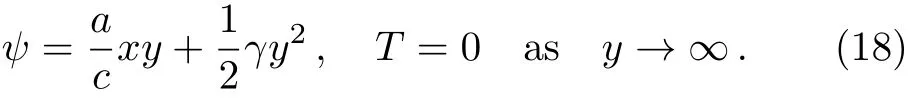
Rewriting the stream function as defined in Ref.[9]
Here f(y)and g(y)represent normal and tangential flow components.Employing Eq.(19)into Eqs.(15)to(18)and integrating once with respect to y,one reaches to following system of non-linear ordinary differential equations:
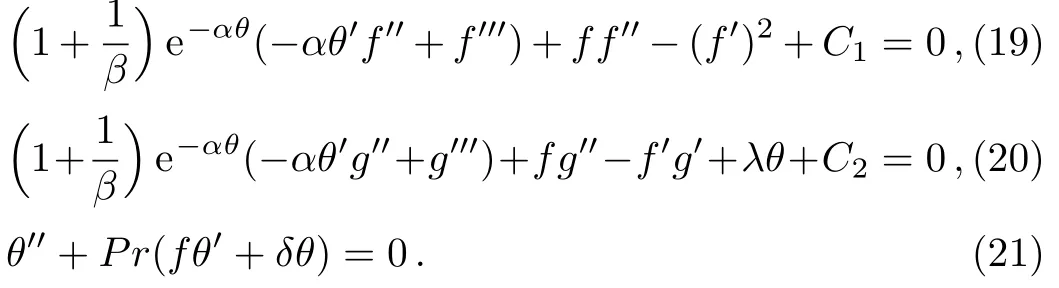
Here the differentiation with respect to y is denoted by primes,C1and C2are integration constants. Consequently,corresponding boundary conditions take the following form:

Constant C1is computed by applying the limit y→∞on Eq.(20)and using boundary condition f′(∞)=a/c.Precisely,we get C1=(a/c)2.From Eq.(20),one can depict that normal flow component is of the form(a/c)y+A as y→ ∞,here A is constant,which is responsible for boundary layer shift.Value of arbitrary constant C2is computed by applying the limit y→∞on Eq.(21)and using the boundary condition g′′(∞)= γ.Precisely,we get C2= −Aγ.Accordingly,Eqs.(20)and(21)take the following form:

Introducing

Using Eq.(26)in Eq.(25)

along with boundary conditions

3 Numerical Solution
The simplified system of Eqs.(22),(24),(27)along with boundary conditions(23)and(28)are tackled numerically by utilizing fourth order Range-Kutta Fehlberg scheme embedded with shooting algorithm.[30]Firstly,higher order boundary value problem is simplified into system of initial value problem by introducing additional conditions in terms of unknown parameters termed as shooting parameters as a substitute of boundary conditions as y→∞.Secondly,this system of initial value problem is solved iteratively and the unknown shooting parameters are determined such that boundary conditions as y→∞are satisfied.Following the above mentioned procedure new variables y1,y2,y3,y4,y5,y6,and y7are introduced as:

By invoking above mentioned substitutions in set of Eqs.(22)–(28)following system is yield:

where,η =1+1/β.
Along with Initial conditions

Here the shooting parameters b1,b2,and b3are initially guessed and afterward determined by means of Newton Raphson’s method for each set of parameter value.The converted initial value problem is numerically dealt by applying integration scheme of fourth order Runge-Kutta-Fehlberg method.Iterative steps are performed till accuracy of ten decimal places is achieved.Computational procedure is performed in computational software MATLAB.
4 Results and Discussion
Present section focuses on examining flow characteristics along with temperature distribution,skin friction and local surface heat flux against significant emerging physical factors.For this purpose Figs.2 to 16 are plotted,which provide graphical illustrations for distinct parameters such as slip parameter ω,heat generation constant δ,variable viscosity parameter α,Prandtl number Pr,Biot number Bi and mix convection parameter λ on normal(f′(y)),tangential(h′(y))velocity components,and temperature θ(y).Streamlines plots for slip parameter ω are also shown to describe the flow pattern in Figs.15–16.

Fig.2 Normal velocity variation for increasing values of ω.

Fig.3 Normal velocity distribution for increasing values of α.

Fig.4 Tangential velocity variation for distinct values of ω.
Figures 2 and 3 reveal the behavior of normal component of velocity.Figure 2 describes the behavior of velocity profile f′(y)for various values of slip parameter ω.Graph shows that f′(y)decreases by increasing slip parameter ω.Figure 3 shows that normal velocity f′(y)decreases with rise in variable viscosity parameter α.Effects of sundry parameters on tangential velocity h′(y)are displayed in Figs.4 to 6.

Fig.5 Tangential velocity distribution for distinct values of λ.

Fig.6 Tangential velocity variation for distinct values of α.

Fig.7 Temperature distribution for increasing values of ω.
From these figures it is witnessed that tangential velocity component accelerates with increase in slip parameter ω,mix convection parameter λ,and variable viscosity parameter α.However,away from the stretching surface this trend altered.Figures 7 to 11 illustrate the influence of slip parameter ω,heat generation constant δ,Biot number Bi,Prandtl number Pr and variable viscosity parameter α on temperature distribution θ(y).It is concluded that Prandtl number Pr contributes in lowering temperature as shown in Fig.10.This happens because Pr being the ratio of viscous to thermal diffusivity leads to lessen fluid temperature.

Fig.8 Temperature variation for increasing values of δ.
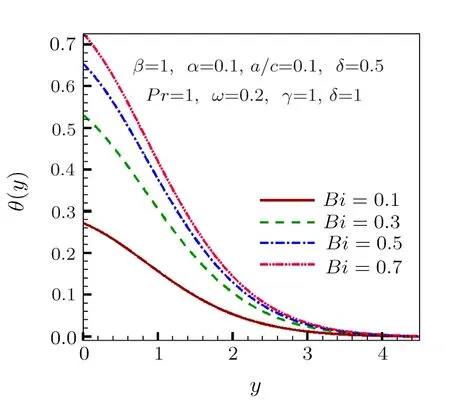
Fig.9 Temperature distribution for increasing values of Bi.
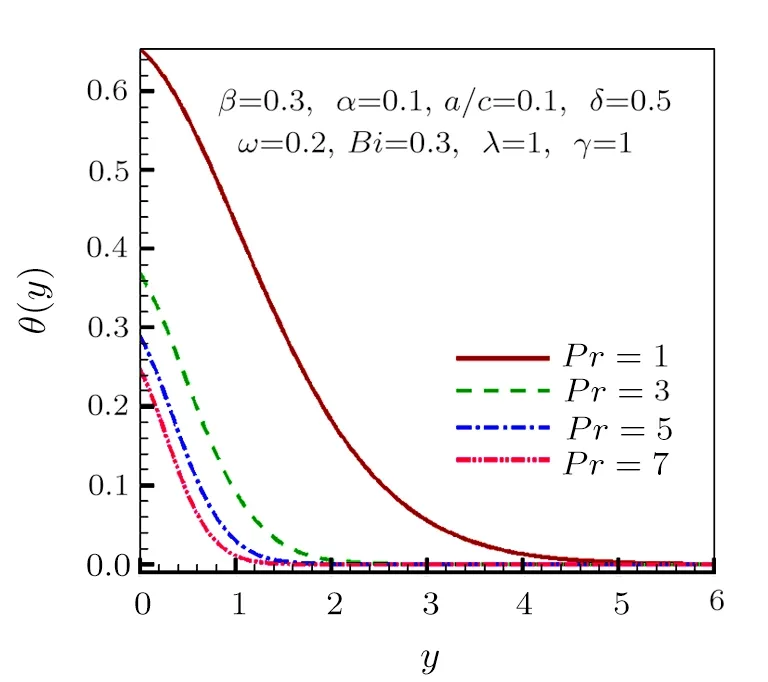
Fig.10 Temperature distribution for increasing values of Pr.
Figures 7,8,9,and 11 illustrate that temperature increases by increasing slip parameter ω,heat generation constant δ,Biot number Bi,and variable viscosity parameter α respectively.Influence of variable viscosity parameter α on normal and tangential skin friction coefficients is shown through Figs.12 and 13.Normal skin friction coefficient f′′(0)decreases with a rise in variable viscosity parameter α as shown in Fig.12,on the other hand,Fig.13 describes that tangential skin friction coefficient h′(0)rises when variable viscosity parameter α increases.

Fig.11 Temperature distribution for increasing values of α.

Fig.13 Variation in tangential skin friction coefficient for distinct values of α.
Figure 14 is sketched to visualize the local heat flux−θ′(0)for distinct values of variable viscosity parameter α.From this figure it is depicted that local heat flux drops with a rise in variable viscosity parameter α.Figures(15)and(16)present streamlines of the flow for different values of slip parameter ω with obliqueness parameter γ =10 and γ = −10.Figure 15 depicts that flow with ω =2 is more tilted towards the left as compared to the flow with ω=0.2 and γ=10.It is observed in Fig.16 that flow pattern is more tilted towards the right with slip parameter ω =2 and γ = −10.

Fig.14 Variation in local heat flux for distinct values of α.

Fig.15 Streamlines for slip parameter ω with obliqueness γ=10.

Fig.16 Streamlines for slip parameter ω with obliqueness γ = −10.
5 Concluding Remarks
Present article examined heat transfer and flow phenomena of a fluid having variable viscosity influenced by mixed convection,partial slip condition and heat generation or absorption.Here fluid was considered to be striking the stretching surface obliquely.Moreover,viscous dissipation effect was ignored and Casson fluid model was incorporated to study viscoelastic fluid rheological characteristics.Governing non-linear ODE’s of physical problem were numerically dealt by means of Range-Kutta Fehlberg scheme along with shooting algorithm.[30]Computational results were extracted out by keeping accuracy up to ten decimals.Influence of effective parameters was discussed through graphs.Core findings of above study are:
(i)Normal velocity profile f′(y)decreases while tangential velocity h′(y)increases with an increases in slip parameter ω.
(ii)Temperature profile θ(y)rises with viscosity variation parameter α,slip parameter ω and heat generation constant δ.
(iii) A decrease is found in normal skin friction coefficient f′′(0)with variable viscosity parameter α,while tangential skin friction coefficients h′(0)enhanced with α.
(iv)Local heat flux −θ′(0)against slip parameter ω dropped with an increase in variable viscosity parameter α.
Present finding may be beneficial and useful in academic research,aerodynamics and marine engineering.
杂志排行
Communications in Theoretical Physics的其它文章
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking∗
- Conditional Lie-B¨acklund Symmetry and New Variable Separation Solutions of the Third Order KdV-Type Equations∗
- Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations∗
- Pair Production in Chromoelectric Field with Back Reaction∗
- Baryogenesis in f(R,T)Gravity∗
