Entanglement Dynamics of Two Atoms in a Double Damping Jaynes-Cummings System∗
2018-11-24ZhiJianLi李志坚JingZhang张静FengXianHuang黄凤仙LiLiCao曹丽丽andZhongWenHan韩忠文
Zhi-Jian Li(李志坚), Jing Zhang(张静),Feng-Xian Huang(黄凤仙),Li-Li Cao(曹丽丽),and Zhong-Wen Han(韩忠文)
1North University of China,Shuozhou 036000,China
2College of Physics and Electronic Engineering,Shanxi University,Taiyuan 030006,China
AbstractThe entanglement between two stationary qubits is a kind of valuable quantum resources in quantum information or quantum network.This paper investigates the time evolution of the entanglement between two atoms,which are initially prepared in the Bell states and each of which interacts with its own cavity field in the identical and non-identical double damping Jaynes-Cummings(J-C)system.It mainly considers the effect of the atomic spontaneous decay Γ and the decay of cavity field κ on the two-qubit entanglement in such system.While causing the decay of entanglement, Γ and κ can also play a positive role in the entanglement evolution,which may imply a way to better control and maintain the entanglement.What is more,the rules governing the transfer of entanglement between two-qubit subsystems in strong coupling regime are finally studied by taking Γ and κ into consideration.
Key words:entanglement,concurrence,detuning,decay
1 Introduction
Entanglement is a nonlocal correlation and also a fundamental feature of quantum mechanics.It plays an important role in quantum information processing,[1]such as quantum teleportation,quantum key distribution,quantum cryptography,and quantum dense coding,etc.And in recent years it has been extensively studied in many different kinds of physical systems,such as trapped ions,[2]cavity quantum electrodynamics(QED)[3]and linear optical systems,[4]etc.Cavity-QED,which focuses on the interaction of atoms and photons within high-finesse microcavities,provides a convenient system for researching the generation,evolution and manipulation of entanglement.
In order to demonstrate the quantum network better,it is necessary to expand the single cavity QED system to double-cavity or multi-cavity systems,through which the spatial separation of atoms(qubits)can be realized and the entanglement between two atoms can be obtained.[5]Yu and Eberly found that two initially entangled qubits which individually interacting with independent environment become disentangled in a finite time,while local decoherence takes an infinite time.[6]Such interesting phenomenon,termed entanglement sudden death(ESD),was extensively concerned[7−16]and also confirmed in experiment.[17−18]Y¨ona¸c et al.studied atom-atom,cavity-cavity and atom-cavity entanglement evolution in double J-C model,[19]and they found that both ESD and entanglement revival are related to the entanglement transfer between atomic variables and photonic variables.According to the Refs.[20–21]derived by Chan et al.,the transfer of entanglement between twoqubit subsystems is governed by two conservation rules,which provide a quantitative understanding of the distribution of entanglement.Real quantum systems inevitably interact with their surroundings,which give rise to the atomic spontaneous decay and the cavity decay.These decays can result in the loss of entanglement[22−27]and can also affect the disentanglement time.[28−30]In fact,it is difficult to have two identical J-C models in experiments.Therefore,it appears of interest to obtain the entanglement dynamics of two independent,damping but not identical qubits in different coupling regimes and to derive the rules governing the transfer of entanglement between two-qubit subsystems.This paper investigates the evolution of entanglement between two initially entangled atoms interacting with two independent vacuum cavityfields.The entanglement dynamics in different coupling regimes and the influence of Γ and κ on it are studied in detail.We mainly consider two cases:the two J-C models both in strong coupling regime and both in weak coupling regime.Moreover,we derive the rules governing the transfer of entanglement between two-qubit subsystems in strong coupling regime.
2 The Single Damping J-C Model
Under the dipole and the rotating-wave approxima-tions,the effective Hamiltonian for damping J-C model can be written as(~=1)[31]

where g is the coupling constant between atom and cavity,a(a†)represents the annihilation(creation)operator of the cavity field. σ+and σ−are the raising and lowering operators of two-level atoms.∆denotes the detuning between the atom and its cavity.Γ is the spontaneous decay rate of the excited atomic state|edue to the photon emission into the continuum of free-space modes excluding the cavity mode.And κ represents the decay rate of the cavity field.
We assume that the initial state for the atom–cavity system is
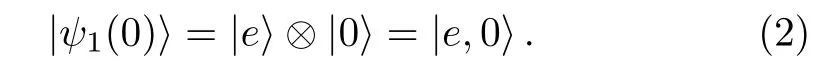
Afterwards,the system will evolve into the state

where x1(t)and x2(t)are the probability amplitudes.Using the Laplace transform techniques,[31]we could obtain the probability amplitudes

For simplicity,from now on we assume exact resonance,∆ =0.Suppose κ = Γ,hence the probability amplitudes in Eq.(4)reduce to

In strong coupling regime g> κ,Γ,the probability amplitudes approximately equal to Eq.(6).For weak coupling regime g< κ,Γ,in the limit of g ≪ κ,Γ(κ − Γ >4g),the probability amplitudes in Eq.(4)reduce to

If the initial state is

it will not evolve with time.So we get

We adopt Wootters’concurrence[32]to evaluate the degree of entanglement.For any two-qubit system,the concurrence can be expressed as

where λi(i=1,2,3,4)are the square root of the eigenvalues of the matrixin decreasing order,with ρ∗denoting the complex conjugation of ρ andrepresenting the Pauli matrixMoreover,the above formula should satisfy the condition 0≤C≤1,where C=0 means no entanglement and C=1 means the maximum entanglement.If a density matrix of a twoqubit mixed state have the“X”form:

where a+b+c+d=1,then the concurrence of this mixed state will be

3 The Double Damping J-C System
As is shown in Fig.1,the double damping J-C system consists of two noninteracting J-C models.In each J-C model,there is a two-level atom S(S=A,B),which couples to a single-mode cavity c(c=a,b)with coupling rate gi(i=1,2).The atoms decay with the rate ΓSand the cavity mode decays with the rate κc.The initial states of the two atoms are assumed to be the Bell states


Fig.1 (Color online)Schematic diagram of the double damping J-C systems.
3.1 Entanglement Dynamics for Initial Bell State
The total initial state of the double atom–cavity system can be written as
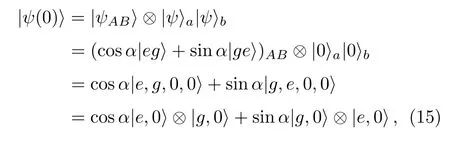

The total density matrix of the system is defined as
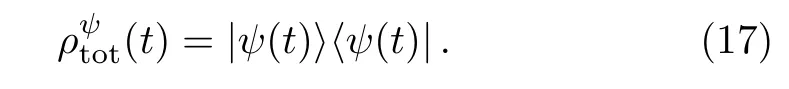
By tracing over the cavity fields,the reduced density matrixof the two atoms can be written as the form of Eq.(11)(see Appendix A).And consequently the concurrence corresponding to the reduced density matrix can be obtained.
3.2 Entanglement Dynamics for Initial Bell State
The total initial state for the double atom-cavity system can be written as

The evolution of the system is given by


The total density matrix of the system is defined as

For this type of total density matrix,we can also get the reduced density matrixfor the two atoms,and consequently obtain the corresponding concurrence(see Appendix B).
4 Discussions and Results
The atom-atom entanglement dynamics is related to the parameters α,g, Γ,and κ. However,different α values do not cause quality difference of entanglement dynamics,[7]so we choose α = π/6 as an example in the following computation.As we know,the coupling strength g affects the oscillation of entanglement,and the difference between the two couplings of each J-C models can affect ESD and entanglement revival.[20]So,in this section,we limit our considerations to the influence of atomic spontaneous decay Γ and cavity decay κ on atomic entanglement in two cases.
4.1 Both in Strong Coupling Regime
To start with,we consider the entanglement dynamics of the atoms in strong coupling regime.According to Eqs.(6)and(A1)–(A7),we can obtain the concurrence CABfor state

where γ is the total decay:

Assuming that the coupling constants are coincident in each J-C model,i.e.,g1=g2=g,the concurrence CABfor statecan be written as
There was one room which she had not noticed particularly; it was empty, except that under each of the windows stood a very comfortable chair; and the first time she had looked out of the window it had seemed to her that a black curtain prevented her from seeing anything outside


Fig.2 (Color online)Evolution of concurrence versus gt and γ/g for state(α = π/6).(a)g1=g2=g.(b)g1=2g2,g=(g1+g2)/2.

Fig.3 (Color online)Evolution of concurrence versus gt for state|ψ(t)(α = π/6).(a)g1=g2=g,(b)g1=2g2,g=(g1+g2)/2.Blue solid line:γ/g=0.6;red dashed line:γ/g=1.
It can be obtained from Eqs.(21)and(23)that the concurrence decays at the rate of γ/4 while oscillating with time;the total decay γ has no influence on the frequency of the oscillations or the entanglement vanishing time.These results are illustrated in Fig.2,in which CABvaries with gt and γ/g.In Eq.(23),according to the zeros of cos2(gt),entanglement periodically vanishes at gt= π2+kπ,(k=0,1,2,...),and similar results can be obtained from Eq.(21).Such behavior is more evident in Fig.3.Obviously,no matter whether the two J-C models are identical or not,the bigger the total decay becomes,the faster the entanglement decays,with Γ and κ being equivalent in their effect on entanglement decay.
Consider now the evolution of concurrence CABfor state|ϕ(t).Likewise,using Eqs.(6)and(A8)–(A14),we can get the concurrence CAB:


Assuming g1=g2=g,the concurrence CABfor state|ϕ(t)can be written as

where

The evolution of concurrence CABversus gt and γ/g is shown in Fig.4,which indicates the total decay can affect ESD and entanglement revival.It can be seen that the concurrence has a similar behavior to that in Fig.2(a)for γg ≥ 1.49.In contrast,for γ/g ≤ 1.49,ESD occurs and revival of entanglement appears after period of time when disentanglement is complete.Similar results can also be obtained from Fig.4(b).

Fig.4 (Color online)Evolution of concurrence versus gt and γ/g for state|ϕ(t)(α = π/6).(a)g1=g2=g.(b)g1=2g2,g=(g1+g2)/2.
Now we focus on the characteristic of the entanglement evolution from Eqs.(25)and(26).For α ≥ π/4,we always obtain Pt>0 whatever γ is,so ESD does not occur.In this case,γ has no effect on the frequency of the oscillations.According to the zeros of cos2(gt),the entanglement vanishes at gt= π/2+kπ,(k=0,1,2,...)with a damping of revival amplitude.For α < π/4,when γ is large,we can always obtain Pt>0,and the behavior of entanglement is similar to the case of α ≥ π/4 or the case of state,as we mentioned above.For α < π/4,when γ is small,we can obtain Pt<0 in the early period,and ESD appears.While as time passes,the concurrence has a similar behavior to the case of α ≥ π/4 as the amplitude of e−(1/4)γtsin2(gt)is becoming smaller and smaller,fi nally leads to Pt>0.Then the entanglement vanishes at gt= π/2+kπ,(k=0,1,2,...).Thus,the evolution of concurrence can be divided into the ESD stage and the non-ESD stage,which is different from the situation without taking Γ and κ into consideration.[6,19]In the ESD stage,we can find ESD and entanglement revival.While in the non-ESD stage,on the basis of the analysis above,the entanglement only disappears at discrete time points.Such behavior is more evident in Fig.5.For α > π/4(the probability amplitude of state|eeis larger than that of state|gg),the ESD does not occur;for α < π/4(the probability amplitude of state|eeis smaller than that of state|gg),the evolution of concurrence can be divided into the ESD stage and the non-ESD stage if γ is large.
Another aspect of interest is how ESD phenomenon is influenced by the value of γ.It can be seen in Fig.4(a)that the disentanglement period decreases with the increase of γ/g in the ESD stage,which can be seen more clearly in Fig.6(a).As is shown in Fig.6(b),proper decay can help to increase the entanglement effectively in the ESD stage.

Fig.5 (Color online)Evolution of concurrence versus gt for state|ϕ(t)with α = π/6,g1=g2=g and γ/g=0.4 The separatrix value between the ESD stage and the non-ESD stage is gt=4.95.

Fig.6 (Color online)Evolution of concurrence for state|ϕ(t)with α = π/6 and g1=g2=g.(a)Concurrence versus gt with γ/g=0.4(blue solid line)and γ/g=1.3(red dashed line).(b)Concurrence versus γ/g with gt=1(blue solid line),gt=2(red dashed line)and gt=4.4(green dotted line).
4.2 Both in Weak Coupling Regime
Unlike the case in strong coupling regime,we have found that the evolutionary behaviors of the concurrence for states|ψ(t)and|ϕ(t)in weak coupling regime are similar.Thus,for convenience,we only show the numerical results of state|ψ(t).To begin with,we study how the atom decay rate Γ affects the evolution of entanglement between two atoms.For the sake of simplicity,we assume the double damping J-C system is formed by two identical J-C models,i.e.,g1=g2=g,ΓA= ΓB= Γ,and κa= κb= κ.Using Eqs.(4)and(A1)–(A7),we can get the concurrence CABfor state|ψ(t).The evolution of the concurrence CABversus gt and Γ/g is plotted in Fig.7(a).
In the following,we study how the cavity decay rate κ affects the evolution of entanglement between two atoms.For simplicity,we also assume g1=g2=g,ΓA= ΓB= Γ,and= κb= κ.The evolution of concurrence CABversus gt and κ/g is shown in Fig.8(a).
Similar to the case in Fig.7,the entanglement decays exponentially with no oscillations or ESD.And κ has a little influence on the decay of entanglement.Surprisingly,the larger the κ/g is,the slower the entanglement decreases to zero,as is clearly shown in Fig.8(b).Comparing Fig.7 and Fig.8,we can see that Γ has a more remarkable influence on the concurrence CABthan κ does.
In the limit of g ≪ κΓ(κ − Γ >4g),using Eqs.(7)and(A1)–(A14),we can get the same simple analytical expressions of the concurrence CABfor both states|ψ(t)and|ϕ(t):

Suppose α is a constant,the entanglement for states|ψ(t)andis only related to Γ and decays with the rate(ΓA+ΓB)/2.
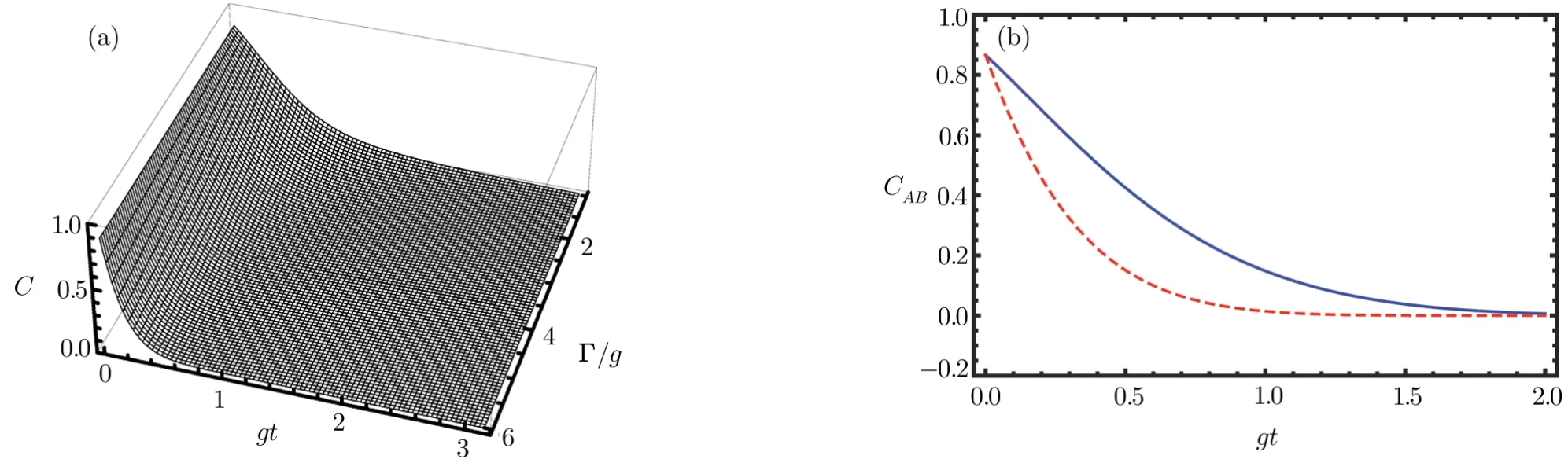
Fig.7 (Color online)Evolution of concurrence for statewith α = π/6,g1=g2=g, ΓA= ΓB= Γ,and κa= κb= κ =3.5g.(a)Concurrence as a function of gt and Γ/g.(b)Concurrence as a function of gt with Γ =g(blue solid line)and Γ=3g(red dashed line).
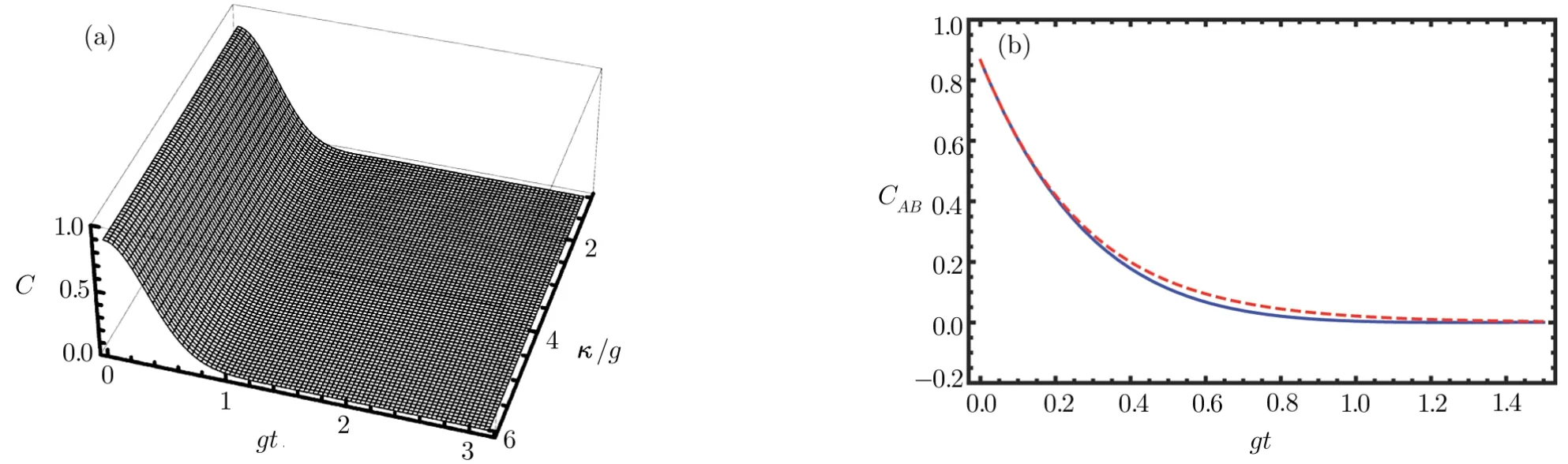
Fig.8 (Color online)Evolution of concurrence for statewith α = π/6,g1=g2=g, κa= κb= κ,and ΓA= ΓB= Γ =3.5g.(a)Concurrence as a function of gt and κ/g.(b)Concurrence as a function of gt with κ =2g(blue solid line)and κ=20g(red dashed line).

Fig.9 (Color online)+++(blue solid line)and e−(γ/2)t(red dashed line)versus gt,for state|ϕ(t)with α = π/6,ΓA= κa=0.4g1,and ΓB= κb=0.3g2.(a)g1=g2=g.(b)g1=2g2,g=(g1+g2)/2.
5 Rules Governing the Transfer of Entanglement
As we have obtained in Subsec.4.1,in strong coupling regime,the entanglement for state|ψ(t)evolves with oscillation;while the entanglement for state|ϕ(t)may evolve with ESD and entanglement revival periods.These behaviors of the entanglement can be understood in terms of the entanglement transfer and the memory effect.[19,23]Decrease or disappearance of the atomic entanglement just means it has been transferred to the cavity field.Due to the memory effect,the photons absorbed by the cavity modes will be coupled back to the atoms in a finite time.According to The transfer of entanglement between two-qubit subsystems is governed by the rules[20−21]

where C12is the global entanglement,and for a double J-C system C12=sin2α.
Adopting the same procedure in Appendix A we can get the concurrence CAb,CaB,and Cab

Then,according to Eq.(21)and Eqs.(30)–(32),we can get


Thus,taking Γ and κ into consideration,no matter whether the two J-C models are identical or not,the global entanglement C12in Eqs.(28)and(29)should be replaced by C12e−(γ/4)t,with γ = ΓA+ ΓB+ κa+ κb.
6 Conclusions
We have investigated the atom-atom entanglement dynamics of the double damping J-C system in vacuum environment.We adopt concurrence to evaluate the entanglement and we find that the entanglement evolution between two atoms shows different behaviors both in strong and weak coupling regime.
In strong coupling regime,the concurrence oscillates with a damping revival amplitude caused by the decay of atoms and cavity field.It can be easily understood that no matter whether the two J-C models are identical or not,the bigger the total decay becomes,the faster the entanglement decays,with Γ and κ being equivalent in their effect on the entanglement decay.For state|ψ(t)there is no ESD whatever the value of Γ and κ are.While for state|ϕ(t)the entanglement may evolve with ESD and entanglement revival periods.Such results can be understood in terms of the entanglement transfer and the memory effect.When the total decay is small,the evolution of entanglement can be divided into the ESD stage and the non-ESD stage.In the non-ESD stage,entanglement only disappears at discrete time points and the total decay only affects its revival amplitude,which is similar to the case of state|ψ(t);while in the ESD stage,ESD and entanglement revival occur and the total decay not only affects the revival amplitude but also affects these two phenomena.Moreover,we find that in certain time span,the disentanglement period decreases with the increases of decay,which may be good for quantum information processing.[33]We also study the rules that govern the transfer of entanglement for states|ψ(t)and|ϕ(t)between two-qubit subsystems when taking Γ and κ into consideration.It is found that,no matter whether the two J-C models are identical or not,the transfer of entanglement between two-qubit subsystems is governed by the two rules(Eqs.(33)and(34)),which help us better understand the entanglement evolution from the perspective of entanglement transfer.
In weak coupling regime,the entanglement decays exponentially with no oscillations and no ESD,which is totally different from the case in strong coupling regime.
In practice,the two J-C models forming the double damping J-C system may not be identical,therefore such a damping and non-identical double J-C system is much closer to reality.In Cavity QED experiments,according to the results derived from this paper,one can choose proper values of Γ and κ to achieve better control of the entanglement between two atoms.Moreover,the method used here is also appropriate for analyzing the double J-C system in other cavity fields such as the coherent state field and the Fock state field,etc.
Appendix A:The Elements of the Reduced Density Matrix ρψ(t)
Based on the procedure described in Subsec.3.1,we can get the reduced density matrix. By tracing over the cavity fields,the density matrixin Eq.(17)can be reduced toin the basis ofIt can be written as the form of Eq.(11).And the elements of the reduced density matrix are:

Then using Eq.(12),we can obtain the concurrence

Appendix B:the Elements of the Reduced Density Matrix ρϕ(t)
Adopting the same procedure in appendix A,the reduced density matrixin the basis ofcan also be written as the form of Eq.(11).The elements of the matrix are:

Then using Eq.(12),we can obtain the concurrence

猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking∗
- Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations∗
- Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
- Pair Production in Chromoelectric Field with Back Reaction∗
- Baryogenesis in f(R,T)Gravity∗
