Kinetic Instability of Anisotropic Drift Wave Accompanied by Field Aligned Currents in Solar Coronal Loop

Hafsa Naim, Ch.Uzma, and G.Murtaza

Salam Chair,Department of Physics,GC University,Lahore 54000,Pakistan

AbstractSolar coronal loops are frequently accompanied by the field-aligned currents,which drive instabilities if the drift velocity u0>vAthe Alfv´en velocity.For our choice of parameters,the critical threshold value of u0/vAis ∼ 3.0 for growth and the corresponding current filling factor∼ 10−3−10−4.Below this value we are no longer in the kinetic regime. The coronal loops also have short-scale density gradients within each loop.The electron resonance in the presence of density gradient causes the drift mode to grow.We study the effect of these two free energy sources,the electron drift and the density gradient,in the presence of temperature anisotropy T⊥α >T∥α.These effects simultaneously exist in the coronae.Using gyrokinetic theory,we investigate the influence of these effects,examine how they interplay with each other and study the consequent growth of the magnetosonic wave.We observe that kinetic instability driven by density gradient can be suppressed by field-aligned currents.The temperature anisotropy with chosen signatures causes further stabilizing effect.The results may prove useful to study the heating mechanism of solar coronal loops,acceleration of particles and confinement of particles in the thermonuclear reactors.

Key words:solar corona,coronal loops,temperature anisotropy,density inhomogeneity,field-aligned currents,gyrokinetic

1 Introduction

Magnetic loops are the basic structural elements of the solar corona,which are actually the closed solar magneticfield lines.Solar coronal heating is still an unresolved puzzle since 1942 when Edl´en,[1]the Swedish physicist,fi rst time predicted the high temperature of the corona in comparison to the lower temperature of the photosphere.The solar corona consists of low-β plasma and is highly structured with a large number of continually developing loops and filaments fabricated by solar magnetic fields as observed by Skylab,SOHO,and TRACE etc.and most of these coronal magnetic loops are current carrying structures.[2−3]

The dynamical structure of the coronal magnetic loops are the result of various processes including foot point motions of the photosphere,oscillations and tangling of loops.[4−6]The loops contribute significantly in the transformation of photospheric energy in to thermal energy in the corona.[7−9]Continuous motions of the foot points in the photosphere give rise to the field-aligned currents in the loops,[10−11]which in turn is the result of fluid motion in the convective zone.High electrical conductivity of the solar plasma causes convective flows to interact with the magnetic field at the foot points of the coronal loops,which results in twisting of field lines.In the coronal loops the magnetic pressure is much greater than the kinetic pressure,so these are the field free zones and the electric currents flow parallel or anti-parallel to the magnetic field lines.Also the field-aligned currents may be due to the flow of charges,which are gathered in the photosphere.[6,12]The field-aligned currents,which are believed to be an important source of coronal heating in closed magnetic regions,cannot be measured directly and can only be estimated from vector magnetograms and radio observations.[9,13−14]In the current carrying coronal loops,the field-aligned drift velocity of the current carrying electrons can be estimated as u0=(4I/πeneD2f)cm·s−1,where I the loop current in CGS units is found to be 3×1020statA,neis the electron density∼ 109cm−3,d is the cross-sectional scale of real current channel,D is the cross-sectional diameter of the loop∼108cm and f=(d/D)2≪1 is the current filling factor ∼ 10−3–10−4.So u0/vAcomes out to be ∼ 1.0–10.0.[3,7]

These fine structures(loops and filaments)play a crucial role in coronal heating.Among several others,the two important coronal heating theories are wave heating theory and the magnetic reconnection(nano-flare heating)theory.[7,15−16]One of the proposed heating mechanisms is through MHD waves.MHD waves are thought to play an important role in coronal plasma heating and solar wind acceleration.We can observe these waves directly in the corona through EUV imaging telescopes on SOHO and TRACE space crafts.Slow magnetosonic waves are inves-tigated by many researchers in the coronal loops.[17−20]The presence of fast magnetosonic waves in the low beta coronal plasma is reported by Thompson et al.[21]Fast magnetosonic wave is an exceptional tool for MHD seismology.

But the present fluid/MHD models are not appropriate because actual heating occurs at much smaller length scales.So a kinetic treatment is needed.We introduce a model based on kinetic theory of obliquely propagating drift magnetosonic wave.The drift mode generally arises due to gradients in density,magnetic field or temperature.While dealing with kinetic drift wave theory,the most important factor for the heating of corona is the existence of density gradients perpendicular to the magnetic field.For the stimulation of drift waves,density gradients become a source of free energy.Drift modes continue to grow both in collisional and collisionless plasma environments in different regions of solar atmosphere and can be explained byfluid model as well as by kinetic model and therefore called universally growing modes.In a collisionless plasma the growth of the mode is the result of electron resonance accompanied by density inhomogeneity,which is exclusively a kinetic effect and cannot be studied by single fluid or MHD model.Similarly different values of electron and ion temperatures Teand Tiin the corona and large temperature anisotropy with T⊥α>T∥αcan only be explained by kinetic theory.So a kinetic drift mode can abide by all the requirements of coronal heating,i.e.,it provides an energy source at extremely high temperatures,is an efficient method of energy transfer to the particles and is applicable everywhere in the corona.[22−23]

We are presenting a different model of coronal loops heating through drift wave accompanied by the fieldaligned currents using gyrokinetic theory.The requisite density gradients are observable in the extended magnetic loops in the entire solar atmosphere.A short scale density variations within each coronal loop discretely is observed in the 3D coronal loops analysis.[24−25]As we are considering low-β plasma,the magnetic field gradient as Ln/LB≈ β/2 can be neglected.[26−27]

With the three free energy sources—field-aligned currents,density inhomogeneity,and temperature anisotropy,we estimate the growth of the drift magnetosonic wave.For clear perception of the problem,we first study their effects on the wave growth and the phase velocity individually,then in pairs and in the end all the three effects together.We observe that the field-aligned currents suppress the kinetic instability generated by the drift in the coronal loops.The stimulation,growth and damping of the kinetic instability is important for understanding the heating of corona and coronal loops and for analyzing the various phenomena,like acceleration of particles,taking place in space,astrophysics and in thermonuclear reactors.

Regarding fusion applications,it is well known that in low-β toroidal devices,the density and temperature gradients are present that can drive the microinstabilities,which pose a serious threat to efficient confinement.[28−30]Further,the field-aligned currents are also present in tokamaks,which constitute another source of free energy.We notice that the simultaneous presence of the two free energy sources(density gradient and field aligned currents)along with temperature anisotropy,produces a stabilizing effect,which can improve the confinement.Gladd and Krall[31]discussed current driven drift waves in reversedfield pinches.

The plan of the paper is as follows:Sec.2 describes the mathematical depiction.Section 3 gives graphical analysis and Sec.4 contains summary and results.

2 Mathematical Depiction

We consider the propagation of drift magnetosonic wave in a low beta anisotropic plasma with field-aligned currents produced by the field-aligned drift of electrons within a loop.Using gyrokinetic variables,the dispersion relation obtained by following the procedure of Naim et al.[16]is given by

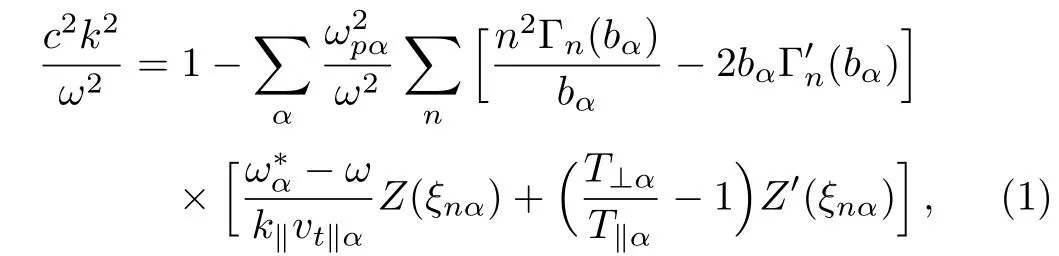
where α is used for species(ions and electrons).=/2ωcαLαis the diamagnetic drift frequency.Γn(bα)=In(bα)e−bαis the modified Bessel function and bα=is its argument.Z(ξnα)is the plasma dispersion function and ξnα(ξni=(ω − nωci)/k∥vt∥iand ξne=(ω − k∥u0− nωce)/k∥vt∥esince we are considering only field-aligned drift of electrons)is the argument of plasma dispersion function.Lnα= −nα0[dnα0(x)/dx]−1is the scale length of density inhomogeneity,which is directed along x-axis,perpendicular to the ambient magnetic field directed along z-axis.

Taking large argument expansion of plasma dispersion function ξnα≫ 1,and small Larmor radii bα≪ 1,assuming ω2≪and after performing some lengthy algebra,[32]we get the ReD(ω,k)and ImD(ω,k)parts of the dispersion relation for anisotropic drift magnetosonic wave with field-aligned currents as

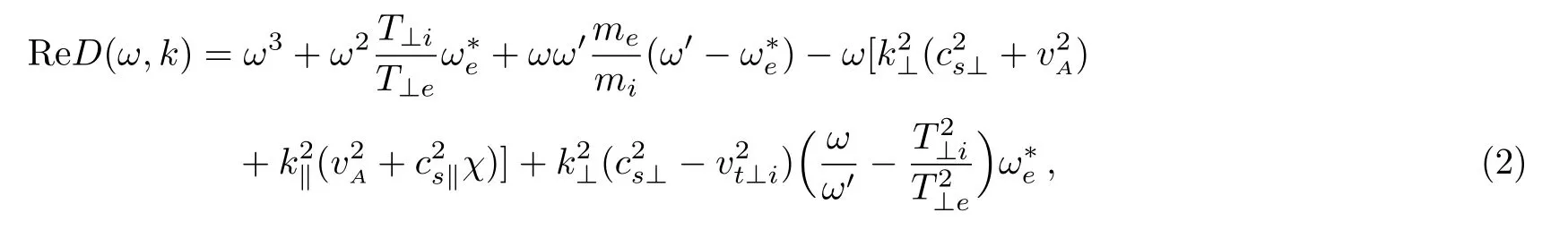
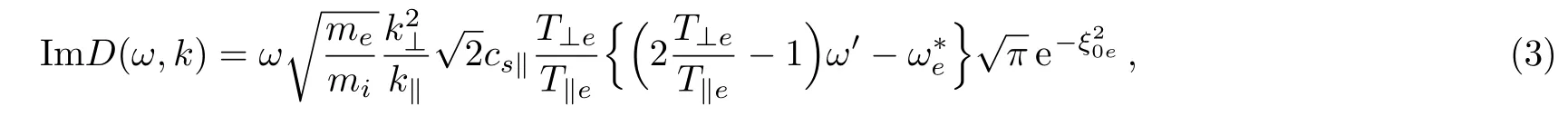
where ω′= ω − k∥u0and u0is the field-aligned drift velocity of electrons,

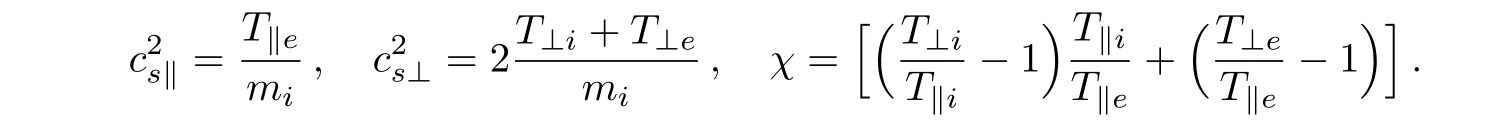
The growth rate of instability is obtained by using the relationas

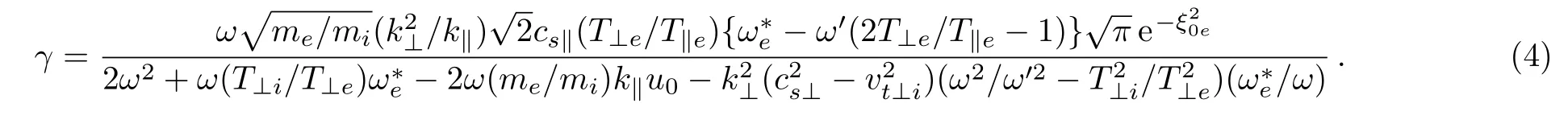
3 Graphical Analysis

We numerically evaluate the above Eqs.(2)and(4)for the following parameters of solar coronal loops,n0=109cm−3,B0=10 G,T⊥i/T∥i=6.75,T⊥e/T∥e=6,=0.002,and η=k⊥vA.The real dispersion relation Eq.(2)is obtained by putting the real part equal to zero,while Eq.(4)gives the growth rate of drift magnetosonic wave with the field-aligned currents in the presence of temperature anisotropy.Equations(2)and(4)are general expressions,which include all the three effectsparallel drift of electrons,density gradient and temperature anisotropy.For better understanding of the interaction of different effects,we first briefly examine them individually.

Considering electron drifting alone assuming density gradient and temperature anisotropy to be absent,the growth rate is given by

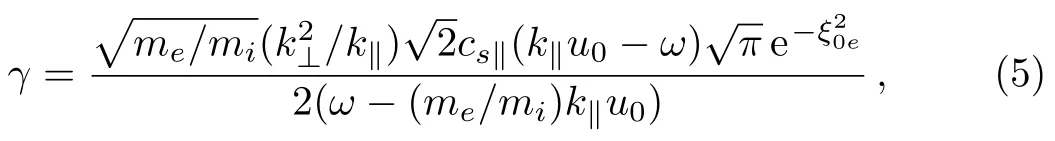
which is graphically represented in Fig.1.

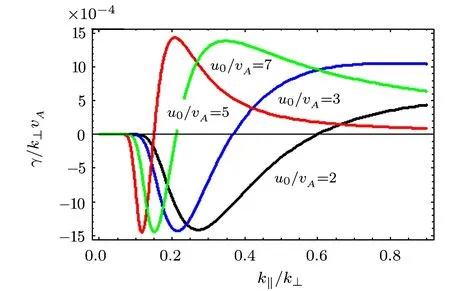
Fig.1 γ/k⊥vAvs.k∥/k⊥,for different values of u0/vA(drift velocity),i.e.,u0/vA=2.0,3.0,5.0 and 7.0.

As is obvious from Fig.1,both damping and growth depend on the value of k∥u0− ω.We also observe that as the drift velocity is increased,the threshold of growth shifts towards lower values of k∥/k⊥.Further,from the real dispersion relation,it is clear that the field-aligned drift of electrons has no considerable effect on the phase velocity of the wave as shown in Fig.2.

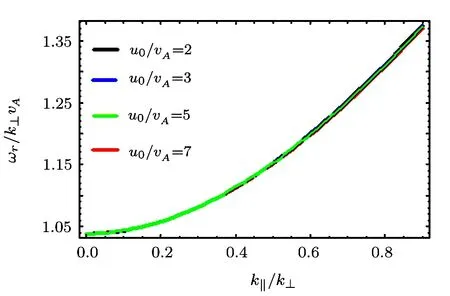
Fig.2 ωr/k⊥vAvs.k∥/k⊥,for different values of u0/vA,i.e.,u0/vA=2.0,3.0,5.0 and 7.0.

Likewise,if we examine the effect of temperature anisotropy alone,the expression for the growth rate becomes

and its graph is obtained in Fig.3.

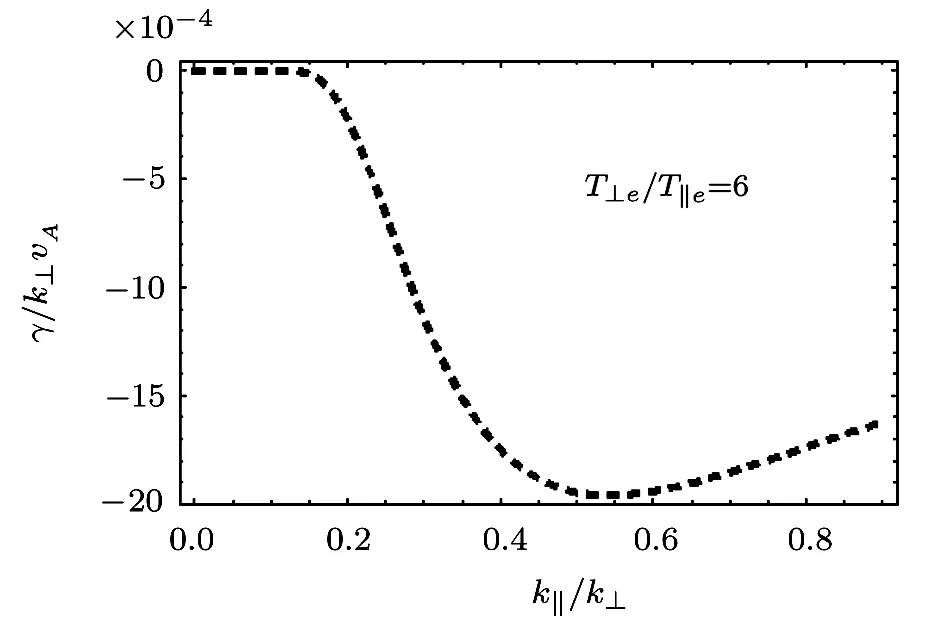
Fig.3 γ/k⊥vAvs.k∥/k⊥,for a fixed value of T⊥e/T∥e=6.0(temperature anisotropy).

We notice that the temperature ratio T⊥e/T∥eis an important factor on which the damping or growth of the wave depends.If T⊥e>T∥e(T∥e>T⊥e)there is damping(growth).The phase velocity of the wave increases with temperature anisotropy as mentioned in our earlier work.[33]

To investigate the independent effect of density gradient,we neglect temperature anisotropy and electron drift velocity,and get the expression for the growth rate as

The plot for the growth is shown in Fig.4.

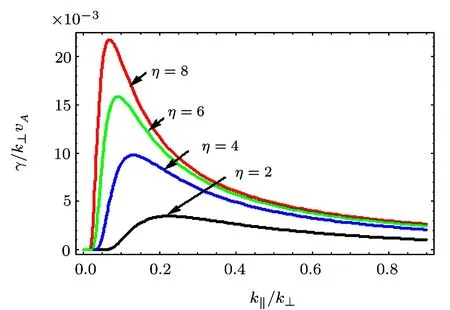
Fig.4 γ/k⊥vAvs.k∥/k⊥,for different values of η (inhomogeneity factor),i.e.,η=2.0,4.0,6.0 and 8.0.

It is obvious that the instability condition for growth is−ω>0.We observe that growth increases with the increase of inhomogeneity factor η.We also realize that the growth of the wave reduces with the increase of parallel propagation component k∥.

The plot of the phase velocity vs.obliqueness k∥/k⊥for different values of η shows that with the increase of density gradient,the phase velocity decreases as shown in Fig.5.

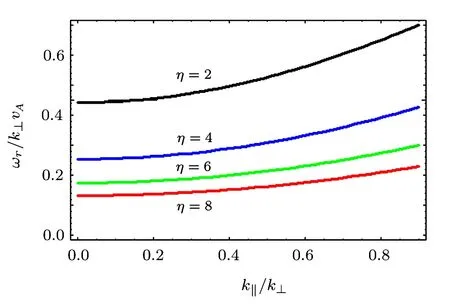
Fig.5 ωr/k⊥vAvs.k∥/k⊥,for different values of η,i.e.,η=2.0,4.0,6.0 and 8.0.

Now to observe the effect of two free energy sources and to investigate their relationship with each other,we neglect density inhomogeneity and obtain the following growth rate

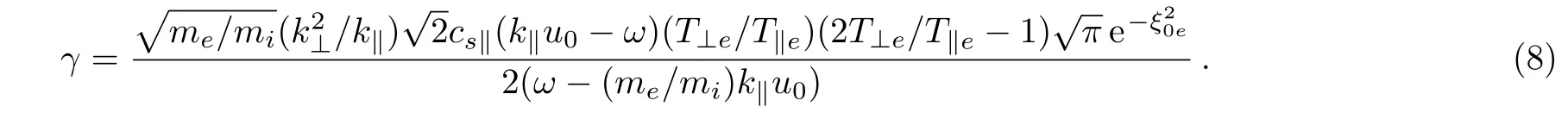
We notice that for growth k∥u0− ω >0(i.e.,the drift velocity u0> ω/k∥the parallel phase velocity)and 2T⊥e/T∥e>1.The temperature anisotropy comes out just as a multiplicative factor and therefore it improves damping or growth of the wave roughly 10 times as is displayed in Fig.6.

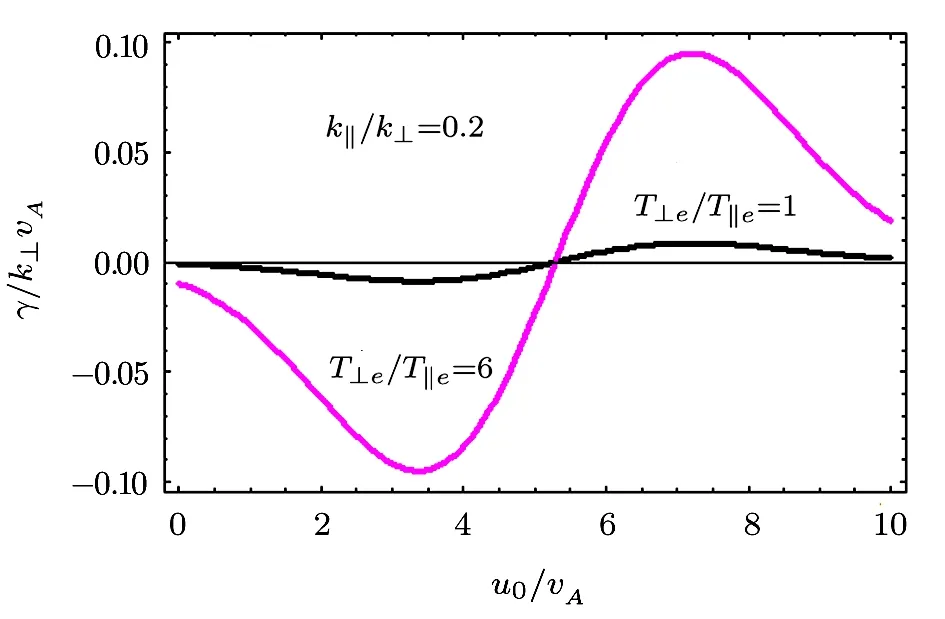
Fig.6 γ/k⊥vA vs.u0/vA,for the isotropic case T⊥e/T∥e=1.0 and the anisotropic case T⊥e/T∥e=6.0.

Regarding phase velocity,we see that it increases with temperature anisotropy as shown in Fig.7.

Fig.7 ωr/k⊥vAvs.u0/vA,for the isotropic case T⊥e/T∥e=1.0 and the anisotropic case T⊥e/T∥e=6.0.

We have seen the effect of temperature anisotropy on drift velocity u0/vA.Now to see the effect of temperature anisotropy on density gradient,we neglect the fieldaligned currents.The growth rate for this case then takes the form

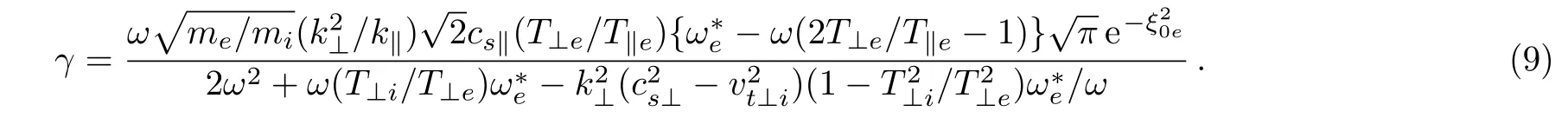
The plot for the growth rate is depicted in Fig.8.

The growth of the drift wave is suppressed by the temperature anisotropy by nearly a factor of 100 as Fig.8 displays.

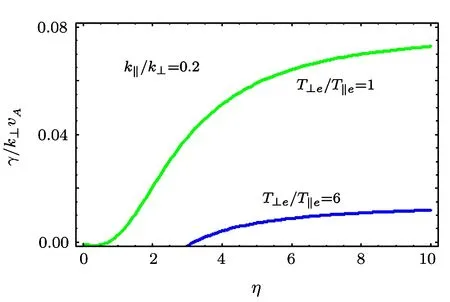
Fig.8 γ/k⊥vAvs.η,for the isotropic case T⊥e/T∥e=1.0 and the anisotropic case T⊥e/T∥e=6.0 for a fixed value of k∥/k⊥ =0.2.

The phase velocity vs.density gradient for isotropic and anisotropic cases is also checked and the behavior is shown in Fig.9.

We see that as η approaches the value near 4,the phase velocity enhances due to the temperature anisotropy.

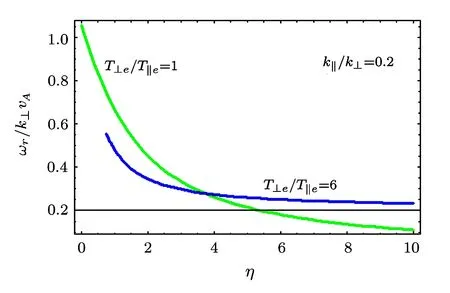
Fig.9 ωr/k⊥vAvs.η,for the isotropic case T⊥e/T∥e=1.0 and the anisotropic case T⊥e/T∥e=6.0 for a fixed value of k∥/k⊥ =0.2.

To see how the density gradient and drift velocity u0/vAinterplay with each other we take Ti=Te.The growth rate then becomes

Figure 10 shows the plots for the growth rate.

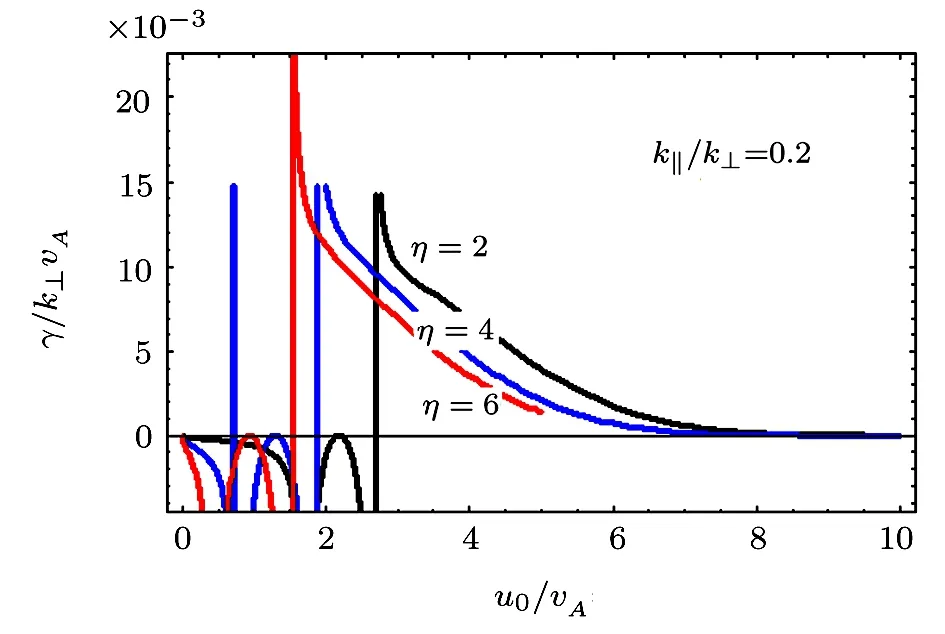
Fig.10 γ/k⊥vAvs.u0/vA,for different values of η,i.e.,η =2.0,4.0,6.0,and for a fixed value of k∥/k⊥ =0.2.

The threshold condition for instability in this case is−ω′>0.For<ω′there is damping of the drift magnetosonic wave in the presence of field-aligned currents and when>ω′growth occurs.We also observe that for the values of η=2.0,4.0,6.0,the growth decreases with the increase of η.In the absence of field-aligned currents,the behavior becomes opposite,i.e.,the growth of drift magnetosonic wave boosts with the enhancement in density gradient.The plots are made for the parameter θ∼ 11.45◦.

So far as real wave frequency is concerned,we find that the phase velocity of the wave decreases for these values of η as depicted in Fig.11.

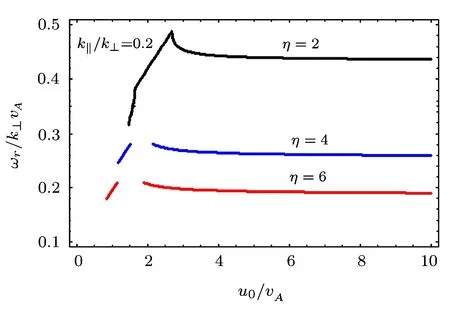
Fig.11 ωr/k⊥vAvs.u0/vA,for different values of η,i.e.,η =2.0,4.0,6.0,and for a fixed value of k∥/k⊥ =0.2.

The combined effect,when all the three free energy sources are present together,is that for a fixed value of k∥/k⊥=0.2 and temperature anisotropy χ =16.5,the growth occurs after a certain threshold value of u0/vA∼3.0 as depicted in Fig.12,which is actually the inverse-Landau damping.Also the growth of the wave reduces with increase of η.Regarding the phase velocity of the wave,it first falls slightly and then becomes constant as seen in Fig.13.We also notice the decrement in the phase velocity with the increase of η.

The kinetic instability of drift magnetosonic wave is driven by the free energy stored in the density gradient in the presence of field-aligned currents.The growth time of the instability τγshould be less than temperature anisotropy relaxation time τAand the diffusion time τDof plasma in the perpendicular direction.[34]The diffusion coefficient for a fixed k can be calculated by using Dk≈ π2γk/k2and the diffusion time τD=L2n/Dkcomes out to be ∼ 1010sec.The growth time of instability τγis very small∼ 10−3sec.It is noticed that even minute density gradient can support kinetic drift instability.

Fig.12 γ/k⊥vAvs.u0/vA,for fixed values of k∥/k⊥ =0.2 and T⊥e/T∥e=6.0 for three different values of η,i.e.,η=2.0,4.0 and 6.0.

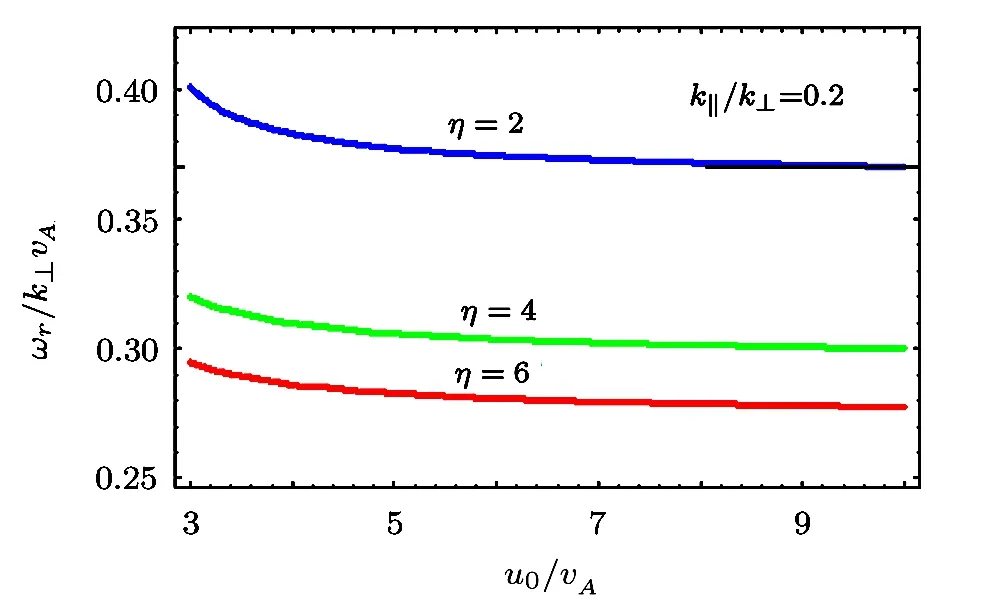
Fig.13 ωr/k⊥vAvs.u0/vA,for fixed values of k∥/k⊥ =0.2 and T⊥e/T∥e=6.0 for three different values of η,i.e.,η=2.0,4.0 and 6.0.

4 Summary and Results

In this work,we have examined the propagation characteristics of obliquely propagating drift magnetosonic mode in an anisotropic,low beta plasma with field-aligned currents in coronal loops.Density gradients are the source of free energy,which are all time present in the coronal regime.Electric currents,constitute another free energy source,may play an important role for solar plasma heating.The solar coronal loops are mostly current carrying loops.These loops are similar to the one found in tokamak plasma regime.[7,10]The currents associated with the coronal loops cannot be measured directly because the surface boundary is not obvious.Zaitsev et al.[35]measured the total current in solar plasma loops using an analog LRC-circuit model.The total current in a loop is found to be I≃ 1012×p−1A1.8×1020statA−4.2×1021statA where p is the period of eigen oscillations(0.7–1.7)sec.We have three free energy sources—parallel drift of electrons,density inhomogeneity,and temperature anisotropy.To facilitate understanding,we have examined their effects one by one,then in pairs and finally all the three effects together.The drift velocity has no prominent influence on the phase velocity but it makes the wave to damp or grow depending on the condition k∥u0−ω <0 or>0.The temperature anisotropy T⊥e>T∥ecauses the magnetosonic wave to damp and increases its phase velocity.While considering density gradient,we find that it reduces the phase velocity of the wave and increases the growth rate of the wave depending on the condition−ω>0.We then investigate these effects in pairs.Regarding field-aligned currents and temperature anisotropy,we observe that as currents cause growth above the point k∥u0−ω and damping below that,the anisotropy just enhances these effects almost 10 times.In the same way,when we consider density gradient and temperature anisotropy,we find that the former shows growth for−ω>0 and the latter suppresses it.When density gradient and drift velocity are considered,we observe the damping of the wave for values−ω′<0 and growth above that.We observe that the growth decreases as η increases.However behavior pattern is different in the absence of field-aligned currents,where the growth increases and the phase velocity decreases with the enhancement of η.

The overall effect of all the three free energy sources is shown in Figs.12–13.The instability driven by density inhomogeneity is suppressed by the field-aligned currents and is due to resonance interaction between the drifting electrons and the drift wave.The condition for the instability is u0>vA.For our parameters,the critical value of u0/vAis∼3.0 below this value we no longer remain in the kinetic regime.For this condition the current filling factor f must be less than 10−3,which is fulfilled in our case.Here we note that with the increase of u0/vAthe phase velocity of the wave initially falls and then saturates.The inhomogeneity reduces the phase velocity as shown in Fig.13.

We conclude that the instability generated by drift can be suppressed by the field-aligned currents in the presence of temperature anisotropy,which enhances that effect.The results may prove useful to study solar coronal heating and to improve the plasma confinement in nuclear reactors.