勾股定理中常见错误例析

管金红

（作者单位：江苏省淮安外国语学校）

本文归纳几种同学们应用勾股定理时常见的错误，并分析出错的原因，望同学们有则改之，无则加勉.

一、注意分清直角边和斜边

【例1】在Rt△ABC中，a=8cm，b=10cm，∠B=90°，求第三边长c.

【错解】由勾股定理，得

c2=a2+b2=82+102=164，

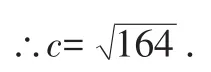
【分析】本题解法中错在没有看清楚所给的条件，思维定式.

【正解】∵∠B=90°，∴b2=a2+c2，

∴c2=b2-a2=102-82=36，即c=6，

∴第三边长为6cm.

二、概念不明确，混淆勾股定理及逆定理

【例2】下列各组数据中的三个数，可作为三边长构成直角三角形的是（ ）.

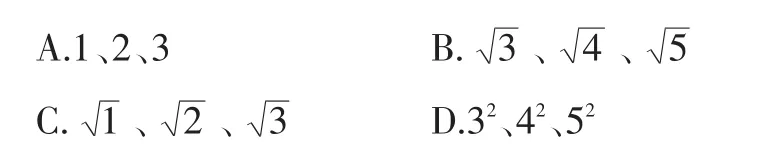
【错解】D.

【分析】对概念的理解流于表面.判断直角三角形时，应将所给数据进行平方看是否满足a2+b2=c2的形式.

【例3】如图1，在B港有甲、乙两艘渔船.若甲船沿北偏东60°方向以每小时8海里的速度前进，乙船沿南偏东某个角度以每小时15海里的速度前进，2小时后，甲船到M岛，乙船到P岛，两岛相距34海里.你知道乙船是沿哪个方向航行的吗？

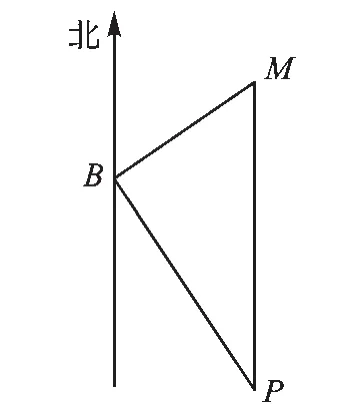
图1

【错解】甲船航行BM=8×2=16（海里），

乙船航行BP=15×2=30（海里），

且MP=34（海里），

∴△MBP为直角三角形，∴∠MBP=90°.

∴乙船是沿着南偏东30°方向航行的.

【分析】虽然最终判断的结果是对的，但解题过程中存在问题.勾股定理的使用前提是直角三角形，而本题需对三角形做出判断，同学们在解题时可千万不能漏步骤.

【正解】甲船航行BM=8×2=16（海里），

乙船航行BP=15×2=30（海里）.

∵162+302=1156，342=1156，

∴BM2+BP2=MP2，∴△MBP为直角三角形，∴∠MBP=90°.

∴乙船是沿着南偏东30°方向航行的.