基于双光束光源的保偏光纤定轴方法研究
2018-11-23贾世甄朱益清姚晓天
贾世甄,朱益清*,姚晓天
(1.江南大学 理学院 光电信息科学与工程系,无锡 214122;2.天津大学 精密仪器与光电子工程学院 光电信息工程系,天津 300072)
引 言
熊猫型保偏光纤在相干通信和光纤传感领域有广泛应用[1-4],其特点是纤芯两侧的两个对称圆形应力区产生残余热应力挤压纤芯产生双折射,形成两个相互正交的偏振轴,进而对沿偏振轴传输的线偏振光有良好的偏振保持能力[5]。在相干通信中,利用其稳定和控制光的偏振态以提高信噪比;在光纤传感中,用其保持相干光偏振态的一致性以提高传感精度。因此,保偏光纤相关应用研究[6-12]和偏振轴的精确定位是相关领域的重要研究课题之一。
国内外学者提出了多种偏振轴定位方案。其中爱立信公司的透镜效应侧视法[13-14](polarization observation by the lens effect tracing,POL)是以侧视成像为基础,具有较高的定轴精度和稳定性,已在光纤熔接机上得到了工程化应用。科研人员为进一步提高定轴精度,多在POL法基础上加以改进,通过改变成像面位置找到山字型[15-16]、五指型[17-18]等特定光强分布,增加特征点的选取数量,使一定角度范围内的定轴精度有所提高,但这对成像面位置的调整要求较高,实用性差,故国内外科研人员仍在研究新的定轴方法[19-20]。
本文中以光纤侧视成像为基本原理,改变以往通过调整成像面位置来增加特征点的思路,采用两对称光束照射光纤来增加特征点,通过仿真和实验证明了本方法不仅有效提高了定轴灵敏度,而且保持了POL法可适用成像面范围广、定轴稳定性高的特点,具有良好的实用前景。
1 侧视成像定轴原理及仿真模拟
1.1 光纤侧视成像定轴原理
当平行光照射在保偏光纤侧面时,由于光纤具有类似柱面透镜的作用,在光纤右侧较大范围成像面上可得特定光强分布,随着光纤旋转,该光强分布也会随之发生变化,选择适当的特征值建立其与偏振轴方位角的关系,通过分析可得以0°为旋转起始位置的标准分布曲线,以任意角度起始的特征值曲线与标准曲线互相关,得到的最大值就是起始角度。
建立光强特征值与偏振轴方位角的标准曲线,两者对应关系可表示为T(θ+θ0),其中,θ表示旋转角,θ0表示起始方位角。将T(θ+θ0)展开成傅里叶级数形式:
cos(nθ)+bn(θ0)sin(nθ)]
(1)
式中,an(θ0)和bn(θ0)为傅里叶系数,an(θ0),bn(θ0)分别为:
cos(nθ)dθ,(n=0,1,2,…)
(2)
sin(nθ)dθ,(n=0,1,2,…)
(3)
由保偏光纤几何对称性得T(θ)为偶函数:
T(θ)=T(-θ)
(4)
且有:
(5)
从而有:
an(0)=0;an(θ0)=0,(n=1,3,5,…)
(6)
bn(0)=0;bn(θ0)=0,(n=1,3,5,…)
(7)
于是可得保偏光纤的初始方位角:
θ0=-arctan{[b2(θ0)/a2(θ0)]/2},(a2≥2a4)
(8)
θ0=-arctan{[b4(θ0)/a4(θ0)]/2},(a2<2a4)
(9)
得到初始方位角θ0后,步进电机带动光纤旋转至偏振轴位置,可得标准光强分布:

(10)
将任意角度起始的光强分布与标准分布进行互相关,并将标准分布按一定步长改变,当相关系数达到最大时,所对应角度即为偏转角度。
1.2 TracePro仿真
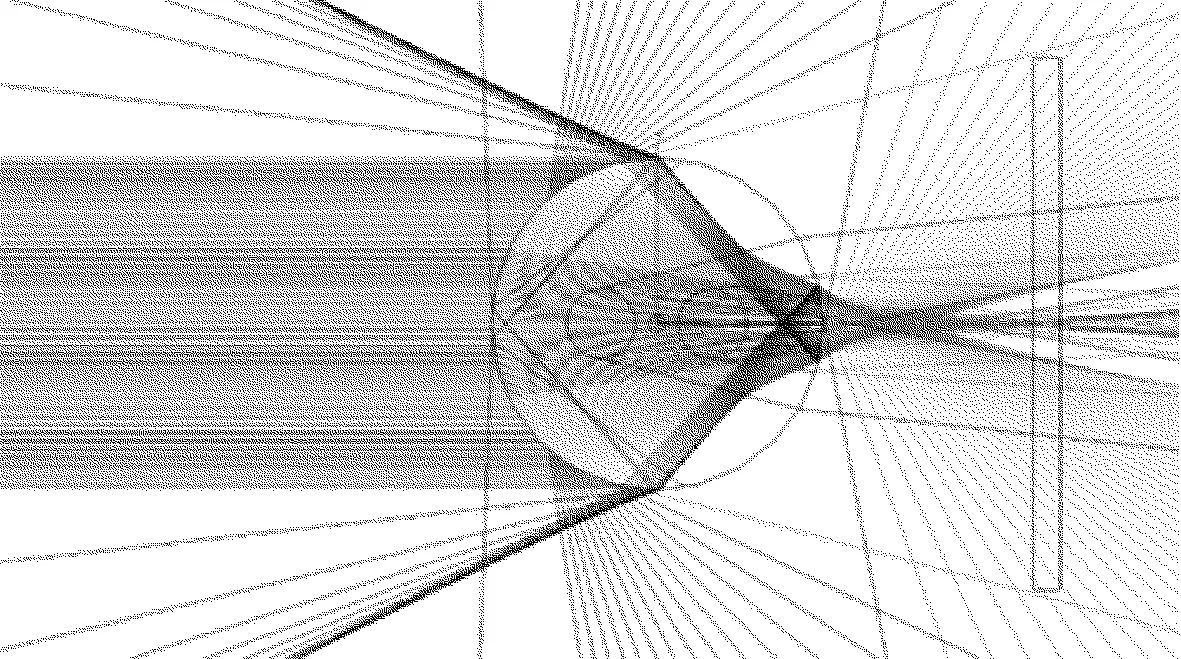
Fig.1 Simulation of side-view imaging of single beam

Fig.2 Side-view imaging simulation of double beam

Fig.3 Light intensity distribution of single beam simulation
图1和图2为在TracePro中建立的熊猫型保偏光纤光线追迹模型。图1为单光束光源侧视成像仿真,单束光从光纤左侧水平照向光纤。图2为双光束光源侧视成像仿真,两束光呈一定夹角照向光纤。由于保偏光纤内部材料的光学特性不同,因此,在光纤右侧的成像面上可形成一定的光强分布图像。如图3所示,单光束照射光纤时,成像面上所成光强分布呈独峰型。如图4所示,双光束照射光纤时,成像面上所成光强分布呈双峰型,旋转光纤使偏振轴的方位角发生改变时,成像面上得到的光强分布也会发生相应变化。

Fig.4 Light intensity distribution of double beam simulation
2 仿真结果分析
2.1 单光束光源侧视成像仿真
以单光束平行光为光源时,选择光强分布的中心峰值为特征值,建立其与偏转角度的对应关系,若光纤偏振轴的起始位置为0°,可得如图5所示的标准特征值曲线。

Fig.5 Standard eigenvalue curve of single beam simulation

Fig.6 Correlation coefficient curve of single beam simulation
将光纤起始位置逆向旋至10°,并以此为起始位置旋转光纤并记录特征值,将得到的特征值曲线与标准曲线做互相关,可以得到如图6所示的相关系数曲线。-10°位置所对应的相关系数为1,即说明光纤偏振轴的起始角度为-10°。
2.2 双光束光源侧视成像仿真
以双光束平行光为光源时,选择光强分布的两最高峰峰值之和为特征值,建立其与偏转角度的对应关系,若光纤偏振轴的起始位置为0°,可得如图7所示的标准特征值曲线。

Fig.7 Standard eigenvalue curve of double beam simulation
将光纤起始位置逆向旋至10°,并以此为起始位置旋转光纤并记录特征值,将得到的特征值曲线与标准曲线做互相关,可以得到如图8所示的相关系数曲线。-10°位置所对应的相关系数为1,即说明光纤偏振轴的起始角度为-10°。

Fig.8 Correlation coefficient curve of double beam simulation
2.3 单光束与双光束光源侧视成像仿真结果对比
由第2.1节和第2.2节中的分析可知,单光束和双光束为光源进行侧视成像时,均可利用互相关分析对光纤偏振轴的起始位置进行定位,但其定位灵敏度与互相关曲线中最高峰的锐度有关[18],最高峰越尖锐说明特征值对偏转角变化越敏感,即定轴灵敏度越高。如图9所示,将单光束和双光束所对应的相关系数曲线绘制在同一坐标系中,可见,两者最高峰所对应的横坐标均为-10°,但双光束仿真相关系数曲线最高峰锐度明显优于单光束仿真相关系数曲线最高峰,由此可见,双光束为光源时定轴灵敏度优于单光束为光源。

Fig.9 Correlation coefficient comparison of single beam and double beam
3 实验论证
为验证双光束保偏光纤定轴法的可行性,利用电动旋转夹具、发光二极管(light emitting diode,LED)、电子显微镜和计算机等搭建实验平台,LED光源与反射镜搭配可形成有一定夹角的双光束光源,光纤夹具在步进电机的带动下能实现固定角度旋转,电子显微镜与计算机构成图像采集系统,通过调节显微镜的物镜可实现成像面的微调,计算机可进行图像处理和数据分析。

Fig.10 Side-view imaging with different imaging surfaces

Fig.11 Side-view imaging comparison of single beam and double beama—single beam b—double beam
在单光束光源照射下,调整显微镜改变成像面位置并采集光纤的侧视成像,如图10所示。不同成像面对应的光纤侧视成像有明显区别,个别成像面可出现五点法、五指法等所需的光强分布。但在较大范围成像面上,中心有明显亮纹的图像,如图11a所示。将单光束光源变为双光束光源,可得如图11b所示的侧视成像,可见有两条明显的亮纹。利用MATLAB对采集到的图像进行光强分析,可得单光束光源侧视成像光强分布,如图12a呈独峰型,双光束光源侧视成像光强分布,如图12b呈双峰型,这与第1.2节中的仿真结果相同,证明利用特殊光强分布增加特征点对成像面位置调整要求较高,而通过增加光源光束增加特征点对成像面调整要求相对宽松,保留了POL法适用范围广的优点。

Fig.12 Intensity distribution of single beam and double beam side-view imaging
a—single beam b—double beam
电动旋转夹具在步进电机带动下旋转,每次旋转后采集侧视成像并记录特征值,如第2.1节中所述,采用单光束光源时,选择光强分布的最高峰值为特征值,如第2.2节中所述,采用双光束光源时,选择光强分布的两最高峰峰值之和为特征值,分别进行互相关运算,如第2.3节中所述,对两互相关曲线进行对比,改变光纤旋转起始角,进行多次实验对比,以互相关曲线中互相关系数由1下降至0所需旋转度数作为互相关曲线锐度的参考量,将统计结果记录在表1中。
Table 1 The rotation angle when cross-correlation coefficient decreased from 1 to 0

experiment numbersingle beam experimentdouble beam experiment128.5°25.1°228.4°25.0°328.5°24.9°428.4°25.1°528.4°25.2°
通过对表1中的数据计算可知,在5次实验中,双光束对应的互相关系数曲线锐度分别优于单光束11.93%,11.97%,12.63%,11.62%,11.27%,即采用双光束光源侧视成像时定轴灵敏度平均优于单光束光源侧视成像11.88%,证明了利用双光束光源来增加特征点数量可以提高定轴灵敏度。
4 结 论
本文中对单光束光源侧视成像和双光束光源侧视成像两种情况分别进行建模仿真,通过对相关性曲线进行对比,证明使用双光束光源有利于提高定轴灵敏度,并通过实验证明了利用双光束产生双峰光强分布具有可行性,进而提出了基于双光束的保偏光纤定轴法。本方法是通过增加光源光束的方式增加特征点的数量,改变了以往通过选择不同成像面,寻找某特定光强分布,增加特征点数量的思路,不仅提高了定轴精度,而且还保留了POL方法成像面易调节、稳定性高的优点。今后可以探究两光束所成夹角和定轴灵敏度间的关系,也可探寻双光束定轴法的最优成像面范围,以进一步提高定轴效果。
