基于全因子实验的激光打孔参量与吸阻关系分析
2018-11-23孙华强李庆坚
孙华强,郇 浩,齐 萌,李庆坚
(山东中烟工业有限责任公司 济南卷烟厂,济南 250104)
引 言
通风率和吸阻是卷烟的重要物理指标之一,它们对卷烟烟气指标有重要影响。通风稀释技术是控制这两个指标最常用的方法,同时也是目前采用的最有效的卷烟减焦降害技术手段之一。传统的通风稀释是通过选用不同透气度指标的接装纸和成型纸来实现的[1-4]。近年来随着激光技术的发展,产生了经过预打孔的接装纸,这降低了控制接装纸透气度的难度[5],但是对有效控制卷烟通风率和吸阻作用效果不明显,直至卷烟在线激光打孔的出现。与预打孔相比,在线激光打孔具有投资少、见效快、可靠性高等特点。目前国内有关卷烟打孔的研究主要集中在激光打孔对单独辅材的研究上,对卷烟在线激光打孔的相关研究较少,对卷烟吸阻的相关研究更少[6-7]。
通过在德国HAUNI公司的LASER 300S型激光打孔设备上设置不同组合的激光打孔参量来分析这些参量对吸阻的影响,以期望通过建立模型,为卷烟在线激光打孔技术在减焦降害生产中的应用提供统计学依据,弥补卷烟在线激光打孔对吸阻相关研究的空白,并为现场吸阻指标的调整提供参考。
1 激光打孔设备的主要参量
在激光打孔参量设置界面,可以看到可更改的参量主要有:烟支直径、孔数、脉冲宽度、功率、布孔偏量、行数、以及通风度控制系列参量。其中烟支直径为参考设定值,孔数和行数在工艺指标值有明确的限定,通风度控制系列参量厂家建议不要改动。因此可以改动的参量有3个:脉冲宽度、功率和布孔偏量。通过查阅设备的使用说明可以明确三者的单位和功能分别为:(1)脉冲宽度(μs)。设定一个激光脉冲的持续时间[8],由于烟支在脉冲期间持续转动,因此脉冲宽度越长,孔长也越长,透气度越大,标准值为50μs;(2)功率(%)。设定激光功率的平均值(本文中无功率测量元件,无确定实际功率值,仅以%为单位来设定界面),使得激光打孔的孔形构成清晰,过高或过低的功率设定都应避免;如果孔被烧灼的边缘偏大,则功率太高;如果孔小或根本没有被烧灼,则功率太低[9],标准值为80%;(3)布孔偏量(%)。为使激光的功率和脉冲长度与生产速度相匹配,以保持透气度和布孔的稳定,影响布孔控制时的振幅,使孔均匀地分布于烟支周边,标准值为10%。
2 因子试验的方案和试验过程
2.1 材料、仪器和分析工具
对细支卷烟(泰山心悦)激光打孔参量和综合测量台(CERULEANQTM系列)采集的吸阻数据进行试验分析,得出彼此之间的相互关系。试验中运用的方法是六西格玛的试验设计方法;使用的工具是MINITAB 16,参见参考文献[10]和参考文献[11]。
2.2 试验水平设定
考虑可能影响吸阻的3个因子,确认哪些因子影响是显著的,进而确定出最佳的参量组合。这3个因子及准备安排的试验水平如下(水平的设定参考标准值和现有值):脉冲宽度(μs),低水平为50μs,高水平为100μs; 功率(%),低水平为70%,高水平为90%; 布孔偏量(%),低水平为5%,高水平为15%。
2.3 试验过程
由于要考虑各因子及其交互作用,因此决定采用全因子试验的方法,并在中心点处进行3次试验,一共11次试验,确定完方案和试验水平后运用MINITAB 16生成试验计划表,按照生成运行序,在综合测量台上逐批测量每种参量组合的样品,保留满足重量、圆周和长度指标的前30组数据得到烟支吸阻的均值填入试验计划结果表[12-14]。表1中列出了标准序、运行序、中心点和区组的数值。
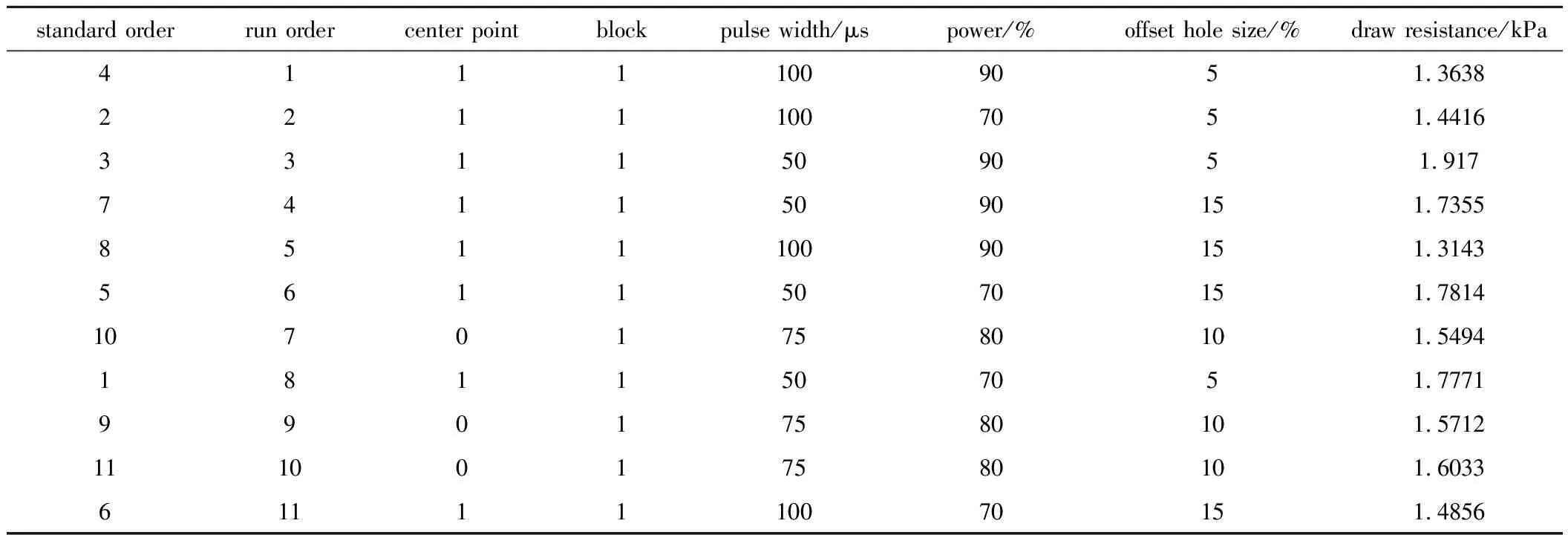
Table 1 Table of experiment parameters
通过得到的吸阻数据可以看出,吸阻的均值为1.5946kPa,中位数为1.5712kPa,标准差为0.1902kPa,极差为0.6027kPa。但无法直观看出3个参量对吸阻的影响规律,必须通过运用工具进行分析。
3 试验分析
3.1 拟合因子试验
借助MINITAB 16就表1中的数据进行分析,首先进行的是拟合选定模型[15],由于考虑3阶及3阶以上的交互作用意义不大,通常可以不考虑,因此只考虑全部因子的主效应和2阶交互效应。由于MINITAB的计算全部是自动进行的[16],其得到的结果见表2。表中,R2为确定系数,Ra2为R2的调整值,Rp2为R2的预测值,S为回归标准误差,Sp2为预测误差平方,P值用于确定检验中原假设的适当性,*表示交互作用。表中的物理量除自带单位的,其它均为归一化单位。
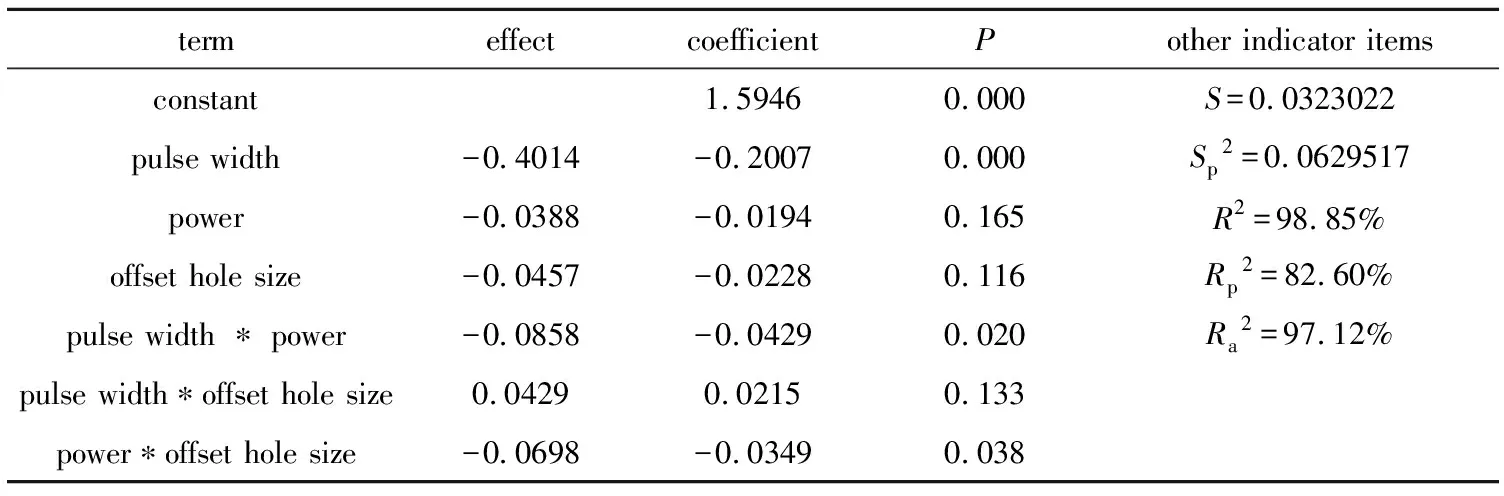
Table 2 Main effect data and the 2nd order interaction effect data in full factorial experiments

Table 3 Variance of draw resistance
表3为吸阻的方差分析。表中,Ss2为连续平方和,Sa2为调整平方和,Ma为调整均方值,F是一个统计量。通过表2中的系数项可以得到吸阻对于3个参量的二次回归方程。下面结合表2和表3对得到的回归模型进行初步分析,以判断模型是否有效,有没有必要进一步优化改进。
3.2 初步分析因子试验设计
3.2.1 分析回归的显著性 (1)模型的整体效果:对应“主效应”和“2因子交互作用”的项目中有两项的P<0.05[17],即可判断本模型总的说来是有效的;(2)模型有无失拟现象:失拟项的P=0.352>0.05,表明无法拒绝原假设,即可以判定本模型没有失拟现象;(3)结果中的弯曲项:弯曲项的P=0.258>0.05,表明无法拒绝原假设,即可以判定本模型没有弯曲现象[18]。
3.2.2 评估回归总效果 (1)对于确定系数:R2=98.85%,Ra2=97.12%,这两个量都接近于1,且两者之间差距不大,表明模型较好;(2)对于S值分析:比较两个模型优劣最关键的指标是看哪个模型能使之最小,此量暂存,等修改模型后再来看此值是否有所降低,以判断模型是否有所改进;(3)对于预测结果的整体估计:R2=98.85%,Rp2=82.60%,二者差距较大,这说明使用现在的模型,会有较多与模型差距较大的点,模型可以进一步改进[19]。
3.2.3 分析各项效应的显著性 计算结果显示,只有“脉冲宽度”的P<0.05,但是“脉冲宽度”和“功率”的交互作用、“功率”和“布孔偏量”的交互作用的P均小于0.05,因此3个主效应都需要考虑。图1为标准化效应的正态图。表示各因子对吸阻的影响,直观地展示了主效应和2因子交互作用显著性。图中α值表示假设检验中的显著性水平。
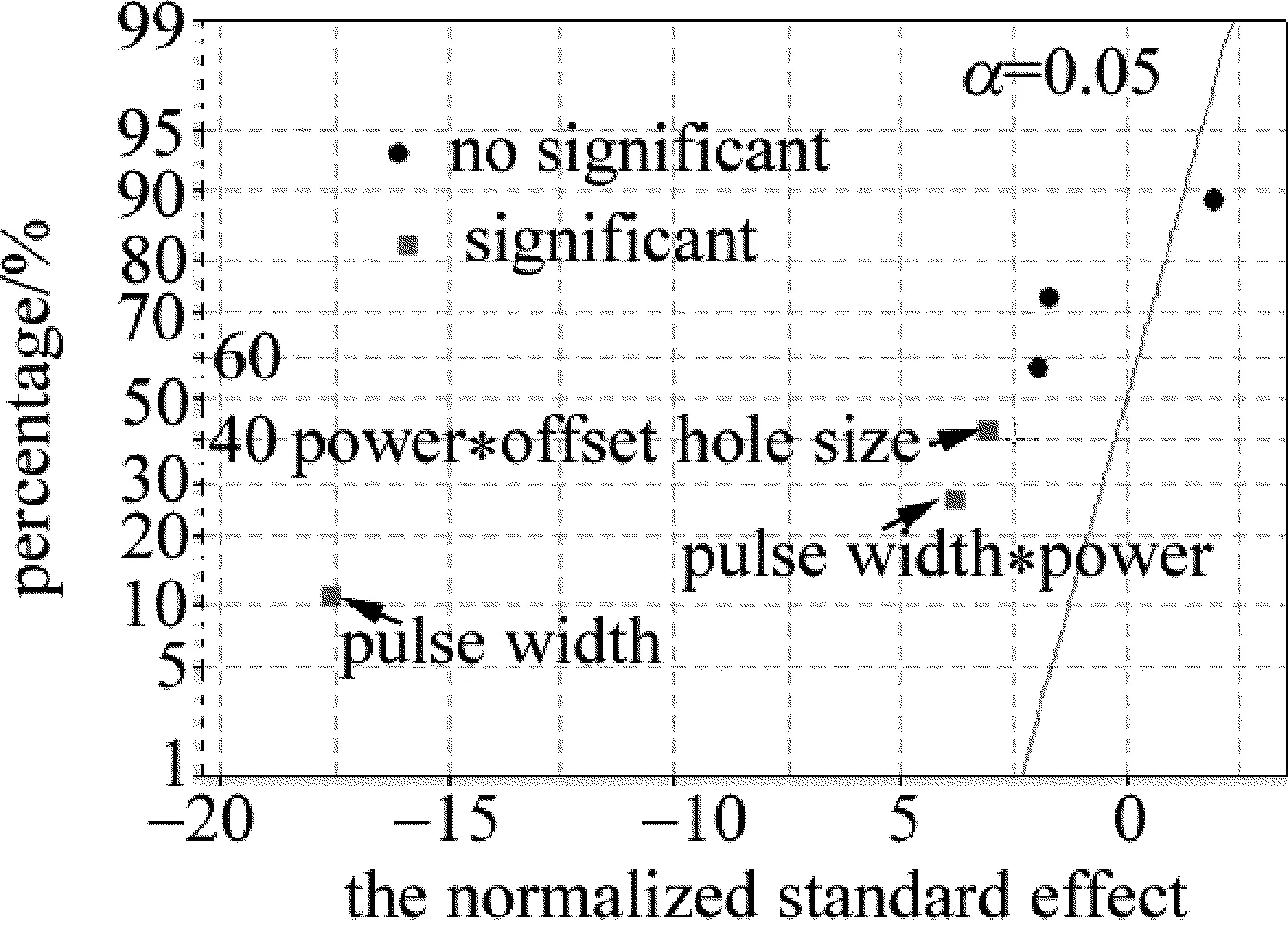
Fig.1 The significance of mecin effect and two-factor interaction effect
3.3 模型优化分析
删减不显著项模型分析,将显著项保留,同时保留与显著项相关的主效应:功率、布孔偏量。重新计算后输出的结果见表4。表5为重新计算后的吸阻的方差分析。

Table 4 Main effect data and the 2nd order interaction effect data after deleting unremarkable items

continue

Table 5 Variance analysis of draw resistance after deleting unremarkable items
通过查看删减后结果的总体效果,如主效应脉冲宽度的P<0.05,表明应拒绝原假设,即可以判定得出本模型总的说来是有效的结论;对应失拟项的P=0.236>0.05,表明无法拒绝原假设,即可以判定:本模型尽管删去了好多项,但并没有造成失拟现象。可以通过表6看出删减后的模型是否比原模型有所改进。

Table 6 Comparison of data before and after the change of model
可以看出,由于模型项数减少了1项,R2通常会有微小的降低(本试验中由98.85%降低到97.83%),但调整的Ra2是否有所提高才是观察问题的关键,本试验中Ra2由97.12%下降到95.66%,可以发现删除不显著的主因子及交互作用项后,回归的效果比原来差了。而S的值从0.0323022提高为0.0396455,Sp2从0.0629517提高为0.0676125,更加强有力地证明删除不显著项后,回归的效果变差了。
3.4 模型选定与分析
通过比较,选定未删减的模型作为获取的最满意模型。将表2中的系数项带入方程式,得到计算机根据实验结果输出的回归方程如下:f(x,y,z)=1.5946-0.2007x-0.0194y-0.0228z-0.0429xy+ 0.0215xz-0.0349yz。其中,f(x,y,z)为吸阻;x为脉冲宽度;y为功率;z为布孔偏量。
通过输出的回归方程系数大致可以看出:3个因子与变量吸阻之间均为负相关关系。这与日常的经验相吻合,即脉冲宽度越大孔会变长进而造成吸阻变小;功率越大孔会越大进而造成吸阻变小。同时因子脉冲宽度的系数相对于其它因子系数要大,即在3个因子同时变化一个单位的情况下,脉冲宽度对吸阻的变化贡献最大,其贡献度约是功率和布孔偏量的10倍。
借助MINITAB 16输出图表功能可以进一步分析。
图2为吸阻的主效应图。从主效应图可以看出,因子脉冲宽度较另外两个因子对吸阻的影响更为显著,还可以看出是吸阻变大,应该让3个主效应因子尽可能小。
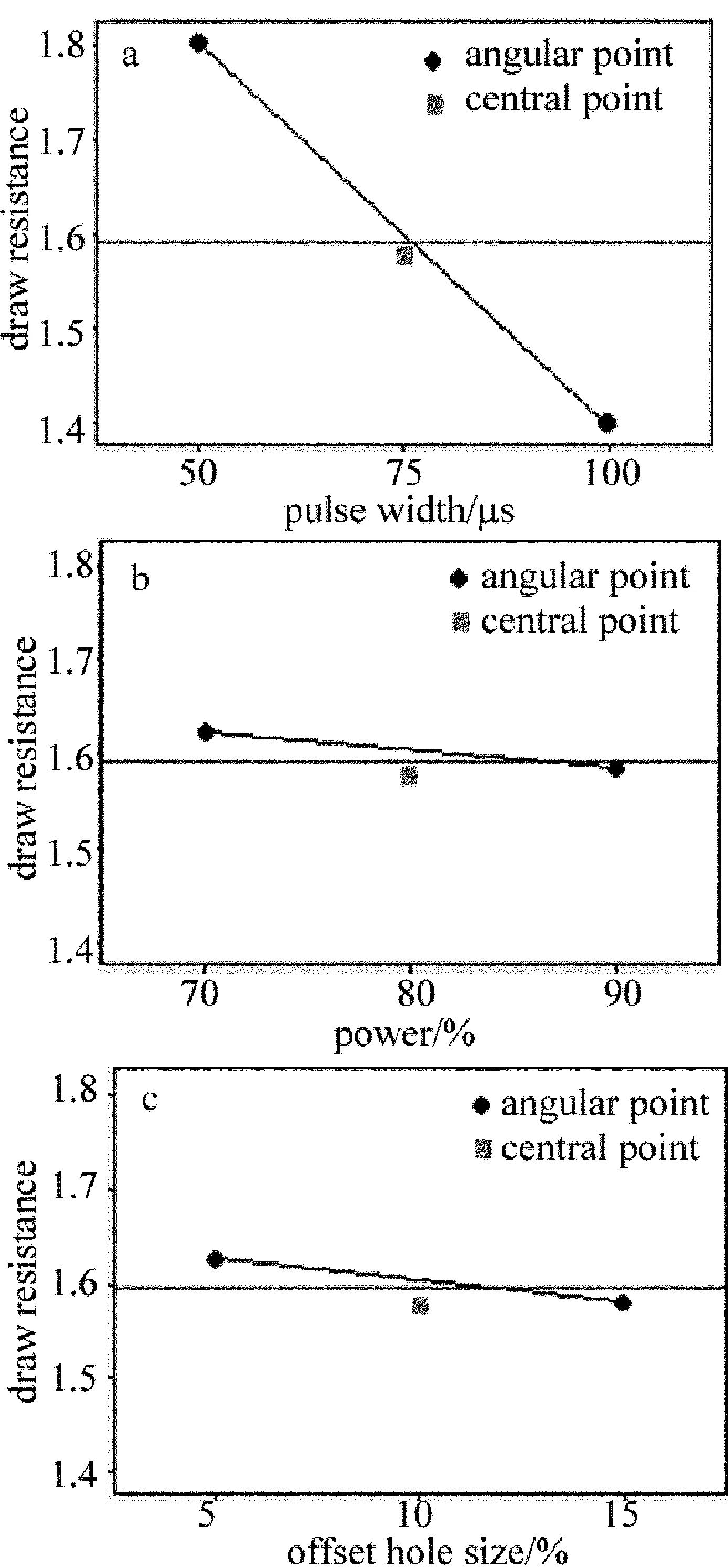
Fig.2 Main effect of three factors on draw resistance
图3为吸阻交互效应图。可以看出,功率因子与布孔偏量因子的交互作用对于吸阻的影响相对于其它因子之间的交互效应要显著得多。
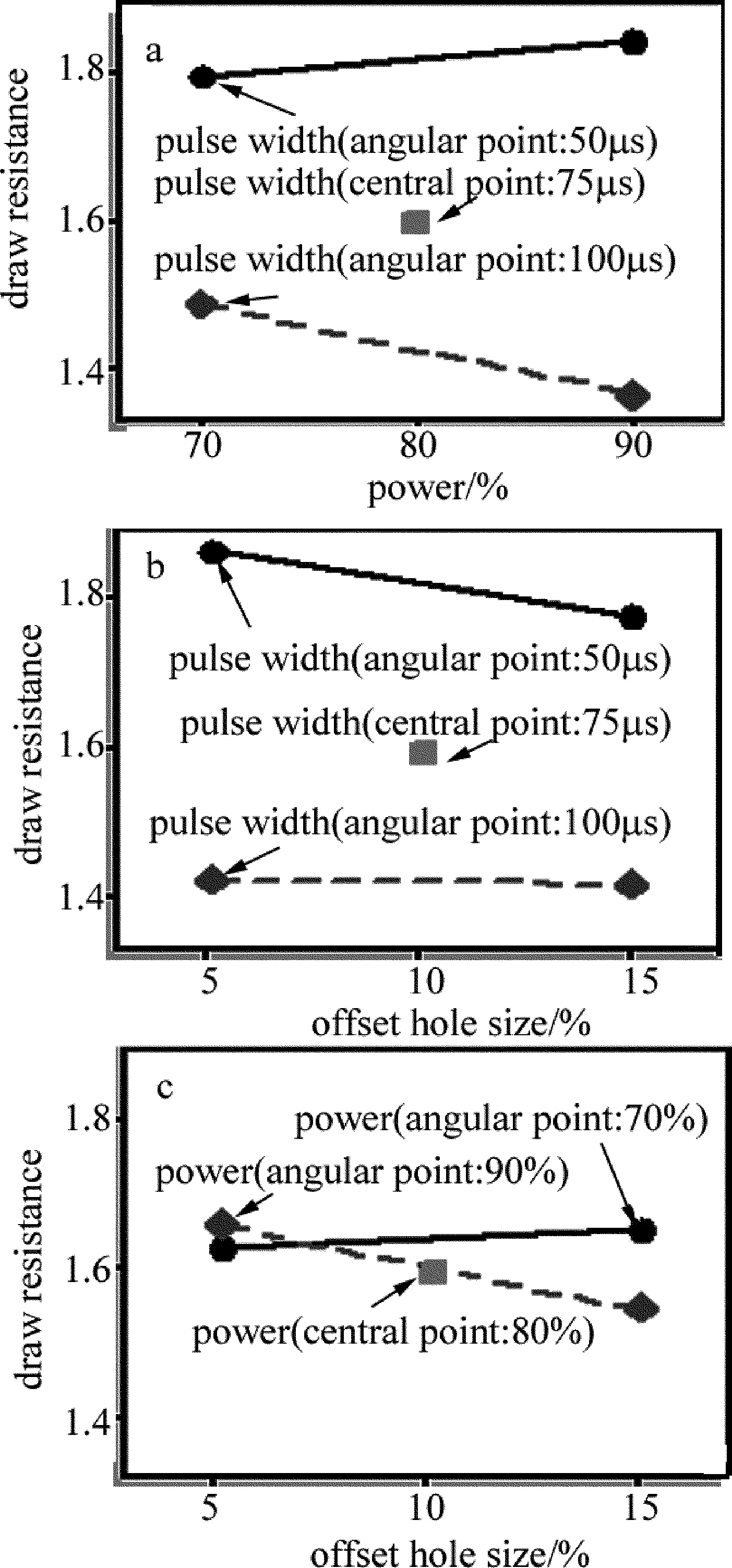
Fig.3 Interaction effect on draw resistance
图4为吸阻的等值线图。可以看出,脉冲宽度因子及与之的交互作用对于响应变量吸阻的影响很显著,为使吸阻变大,应该让脉冲宽度尽可能小。通过等值线图可以直观地看出两个不同的主要因子的设定下,吸阻所在的大致范围以及吸阻随各主要因子的变化趋势[20]。这可以指导进行快速设定。
根据工艺标准要求,不同品牌卷烟的吸阻需维持(1.35±0.2)kPa,从响应优化曲线可以看出[21],当脉冲宽度取93.8426μs、功率取90%、布孔偏量取15%时,吸阻会达到期望值1.35kPa。运行序3的3个因子设置最接近上面的最优设置,只有脉冲宽度不一样取的是100μs,试验中所得数据是1.3143kPa。按照之前的主效应图可以判断出,当脉冲宽度从100μs变小为93.8426μs的过程中,吸阻会变大,因此预测的最优解与实际试验结果很接近。如果与试验结果相差较远,可以考虑在本次获得的最佳点附近继续做试验。根据经验,最优点就在附近,可选择响应曲面方法,其结果要更精细一些。
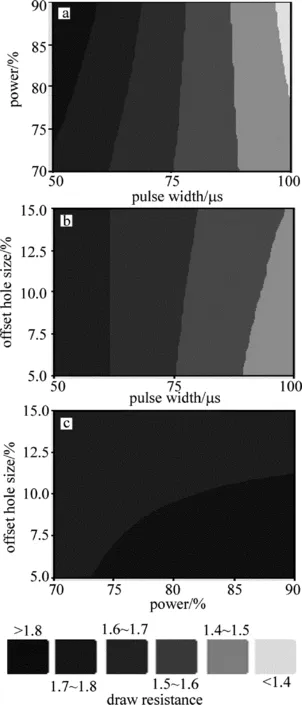
Fig.4 Contour map of interaction effect on draw resistance
4 结 论
通过试验得到的方程可知,脉冲宽度相对功率和布孔偏量对吸阻的影响更为显著。还可以看出,为使吸阻变小,应该让3个主效应因子尽可能大。这与日常的经验即脉冲宽度越大孔变长、功率越大孔越大进而吸阻变小相吻合。同时,功率因子与布孔偏量因子的交互作用对于吸阻的影响相对于其它因子之间的交互效应要显著得多。根据方程所反映的规律,结合现场数据进行分析并及时指导设备调整,可以确保产品质量合格的目的。
以上试验结论是基于同一批次产品共采集的500多组数据得来,试验过程中未考虑烟丝指标、滤嘴棒指标、原辅材料等指标,因此试验数据不能保证适应于所有批次的产品。但该研究可以反映出各项参量对吸阻指标影响显著性的大小,以及3个激光打孔参量影响吸阻指标的趋势。通过后期重复试验,验证了现场调整的结果符合试验的结论。这种方法得来的关系方程和吸阻变化规律在其它研究中没有先例。试验充分利用现场大量的数据结合统计学方法和MINITAB软件将原有的经验更加科学直观地呈现出来,试验方法具有普遍性,可以推广至类似的数据分析使用。
