小波变换和菲涅耳变换的多彩色图像加密
2018-11-23曾健清
曾健清,王 君,陈 叶,刘 琦
(四川大学 电子信息学院,成都 610065)
引 言
随着互联网和多媒体的迅猛发展,信息安全领域面临着越来越多的挑战。光学信息安全技术由于其并行性、快速和高加密维度等特点,正在信息安全领域发挥着越来越重要的作用。在该领域众多的加密系统中,REFREGIER与JAVIDI提出的双随机相位编码系统[1]是最引人注目的,该加密技术采用4f系统来实现:把两块随机相位掩模分别放入系统的输入平面和傅里叶频谱面,对原始图像的空间信息和频谱信息做随机编码,这样可以将输入的图像编码成复平稳的白噪声[1-6]。该系统衍生出来的基于菲涅耳域的双随机相位编码加密系统,该加密系统最大的特点是有两个可变换参量,菲涅耳变换相比于其它变换具有更高的安全性,并且不需要光学透镜,与此同时,两块相位板、衍射的距离和波长都可以成为密钥,增加密钥的容量,可控性强[7-8]。
目前,随着互联网技术的迅速发展,数字图像信息量与有线网络的传输能力相互制约,因此,图像的压缩与加密成为了实际应用的研究热点。为了解决图像加密后的传输效率,人们对加密系统的容量要求变得越来越高[9-12]。于是一些图像加密与压缩的光学加密算法相继出现。比如,LIN等人提出了一种基于混沌的图像压缩加密算法[13]。XU等人提出了离散余弦变换与脱氧核糖核酸运算相结合的图像压缩加密算法[14]。虽然这些算法都可以对图像进行压缩与加密,且具有较好的加密效果,但是加密的安全性需要进一步提高。然而这些加密方法将多图像压缩成复合图像时,易产生串扰,导致解密时,图像失真较大,解密质量不佳等特点。
为了解决图像加密后,数据量大且传输速率慢的问题,本文中先利用光学小波变换[15]对多幅彩色图像进行压缩然后利用菲涅耳变换来加密图像信息。本文中的加密算法不仅具有传输速度快、占用空间小的优点,同时还能使图像加密效果得到显著提高,保证了图像加密后安全性高。仿真结果表明,相比于其它图像压缩加密算法,该算法在面对统计分析、噪声攻击、以及裁剪攻击等手段时,具有很好的鲁棒性。
1 理论分析
本加密方法结合了离散小波变换和菲涅耳变换。为了阐述该加密方法,图1是本方法的加密过程和解密过程的系统图。图中,DWT是离散小波变换(dis-crete wavelat transform),FT表示菲涅耳变换(Fresnel transform),IFT表示菲涅耳逆变换(inverse Fresnel transform)。
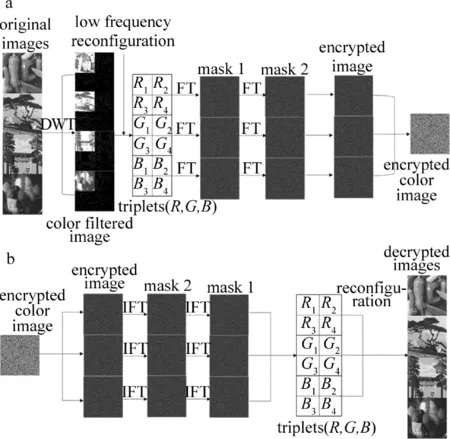
Fig.1 Schematic diagram of the proposed encryption schemea—encryption process b—decryption process
1.1 图像压缩
对于2维信号f(x,y),若母小波函数为h*(x,y),则f(x,y)的小波变换可描述为:
Wf(u1,u2,v1,v2)=DWT[f(x,y)]=

(1)
在频率域表示为:
Wf(u1,u2,v1,v2)=DWT[F(η,ζ)]=
exp[j2π(v1η,v2ζ)]dηdζ
(2)
式中,(u1,u2)是伸缩因子,(v1,v2)是移位因子;F(η,ζ)是2维信号的频谱,H*(u1η,u2ζ)是小波谱,exp[j2π(v1η,v2ζ)]是相位因子。
图像压缩方案如图2所示。采用光学系统通过Dammann光栅上光学多通道系统的多参考匹配滤波器实现2维小波变换。将4副原彩色图像Om(x,y)(m=1,2,3和4)先后通过空间光调制器输入系统并与Dammann光栅相乘,经过透镜后,能在透镜1的后焦平面上实现被复制频谱F(u,v)的2维阵列,然后经过第2个透镜的傅里叶变换作用,在输出面板上实现每个子小波的2维小波变换。由于每幅图像必须由相应的子小波处理,因此需要在第1个透镜的后焦平面上引入一个频谱阵列的多参考匹配滤波器(常见的小波函数的傅里叶变换均为正实值,而多参考匹配滤波器能由计算全息产生,并加载在空间光调制器上),该滤波器每个频谱对应一个不同子小波的傅里叶变换,每个频谱的位置与被复制的图像进行相应的位置匹配。
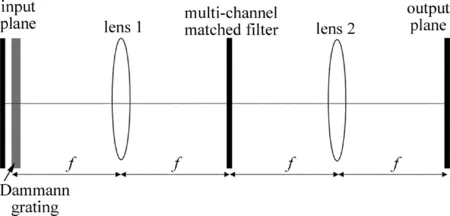
Fig.2 Optical graph of 2-D wavelet transform
因为输出面板是输入面板的一副图像,所有变换相互叠加起来,并行显示小波分解,所以用不同的参考光来对不同的子小波进行编码,从而在输出面板上得到空分复用[16-17]。4个原始彩色图像可分别由光学系统分解,其公式如下:
(3)
式中,O1,O2,O3,O4是4个原始彩色图像,(x,y)表示图像的像素坐标,km(m=1,2,3,4)是离散小波变换谱。最后在CCD上依次获取通过光学小波变换的图像并传输到计算机中。计算机通过使用低通滤波器来提取km的低频部分从而滤掉高频部分以获得4个滤波图像tmi(m=1,2,3,4;i表示R,G,B)。为了减少传输通道和加密数据量,4个滤波图像的每个颜色分量在计算机中重新组合成三元组fi(x,y)(i=R,G和B)如图1所示,表示为:
fi(x,y)=
{t1i(x,y),t2i(x,y),t3i(x,y),t4i(x,y)}
(4)
1.2 图像加密系统
为了进一步提高明文的安全性,使用了一个菲涅耳衍射加密系统,如图3所示。U代表要编码的三元组图像fi(x,y)(i=R,G和B),M1和M2代表两相位掩模,它们在[0,2π]中是随机分布的,在统计上是独立的。产生波长为λ的准直平面波来照射系统,三元组图像fR(x,y),fG(x,y)和fB(x,y)依次经过菲涅耳衍射加密系统。经光学衍射加密系统编码后,由CCD相机记录衍射强度图案。

Fig.3 Optical setup for the proposed optical security system
在图3所示结构中,入射到随机相位板M2的光波前可表示为:
∬fi(x,y)M1(x,y)×
[exp[jπ(x-η)2+(y-ζ)2]/(λd1)]dxdy
(5)
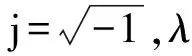
fi(η,ζ)=FT[fi(x,y)M1(x,y);d1]
(6)
因此,输出平面CCD所获取的强度图像可以表示为:
Ci(μ,ν)=|FT{FT[fi(x,y)M1(x,y);d1]×

(7)
式中,| |表示取模运算,(μ,ν)表示CCD平面的坐标,M2(η,ζ)是随机矩阵,图像Ci(i=R,G和B)是三元组图像fi(x,y)(i=R,G和B)对应的子密文,d1和d2分别表示M1到M2以及M2到CCD平面的衍射距离。彩色图像I(μ,ν)是组合图像Ci(i=R,G和B)最终的密文。
1.3 图像解密
解密是加密过程的逆过程,如图1b所示。首先,在计算机中将密文I(μ,ν)中提取Ci(i=R,G,B)后,将Ci(i=R,G,B)传播回菲涅耳衍射加密系统的输入面,计算公式如下:
fi(η,ζ)=IFT[IFT[Ci(μ,ν),
-d2]M2(η,ζ)*,-d1]
(8)
式中,*表示共轭。重建的图像fi(η,ζ)(i=R,G和B)是彩色密文的解密图像的三元组。然后,原始彩色图像Om(m=1,2,3,4)可以通过重构从fi(η,ζ)(i=R,G和B)的R,G和B分量来解密出原始图像。
2 计算机仿真实验以及评估
为了检查作者所提出的方案的性能,使用MATLAB进行了几个数值模拟。在本节中,从统计特性,密钥空间和一些攻击方面来分析加密方案的安全性,并分析评估解密图像的质量。
2.1 加密方案的有效性分析

Fig.4 Image encryption
a~d—the original color images of peppers, trees, lake and fruits respectively e~g—the encryption ofR,G,Bh—the encrypted color-image
图4a~图4d中是4副彩色原始图像,分别为“peppers”,“tree”,“lake”,“fruits”,其大小为256×256像素。计算机模拟中,光波波长λ=632.8nm,衍射距离为d1=d2=50mm。图4e~图4g分别为图像fi(x,y)(i=R,G和B)对应的加密图像,其像素大小为128×128。图4h是将3幅R,G,B分量在计算机中合成为一副彩色密文I(μ,ν),其大小为256×256像素。从密文I(μ,ν)可以看出,原多幅彩色图像的信息加密成了单幅彩色密文,极大地减少了数据量。Cxy值通常被广泛用作评估图像质量的客观测量,其值在0和1之间。它们的值越接近1,恢复图像的质量越好。
(9)
式中,xl和yl是图像中两个相邻像素的值,并且L是图像像素点的总数。图5a~图5d所示是对应的解密图像,其大小为128×128像素,相对于应的Cxy值分别为0.9913,0.9936,0.9970和0.9950。从表1可以看出,与参考文献[18]中的解密图像质量对比,本文中提出的加密算法提高了解密图像的质量。

Table 1 Cxy values of the decrypted images

Fig.5 The decryption of images
2.2 统计分析
通过计算图像加密前后的灰度直方图和加密图像与原始图像之间的相关性,可以分析加密算法抵抗统计攻击的能力。
图6a~图6d上面的小图分别是原图“peppers”,“trees”,“lake”和“fruits”的灰度直方图,图6e上面的小图是当4个图像被加密成一副密文的直方图。显然,加密图像的直方图与原始图像的直方图显著不同。同时也说明加密前后图像的统计信息是完全不同的,即原始图像信息不能通过统计法从加密图像中获得。
图6a~图6d下面的小图分别是原图“peppers”,“trees”,“lake”和“fruits”的相关性图,图6e下面的小图表示加密后的彩色密文图像的自相关性图。可以发现,原始图像的相邻像素高度相关,而加密图像的相邻像素之间的相关性非常小。这两个测试表明,未经授权的用户不可能通过统计分析方法获得原始图像的有效信息。因此,该方案能有效抵抗统计分析的攻击。
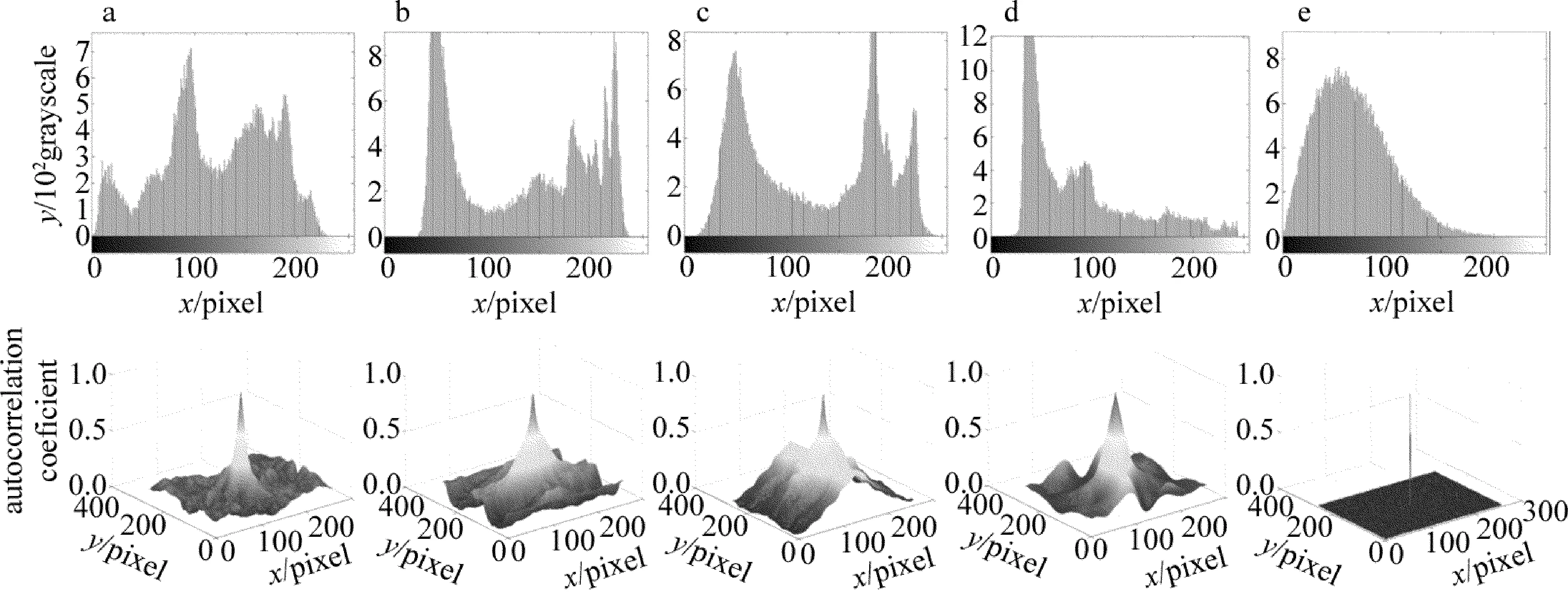
Fig.6 Gray-level histograms and auto-correlation pictures before and after encryptiona—peppers b—trees c—lake d—fruits e—the color encrypted image
2.3 安全分析
一些攻击,如已知明文攻击,选择明文攻击和选择密文攻击,常被用来评估加密系统的安全性。本文中提出的用小波变换和菲涅耳变换相结合的方案在抵抗噪声和遮挡攻击方面起着重要的作用。
在菲涅耳衍射系统中,波长λ和衍射距离d1和d2被认为是解密的密钥。为了评估这些密钥的性能,本文中给出解密的彩色图像相对于波长λ和衍射距离d(d1,d2)的偏差Δλ(20nm)和Δd(20mm)的均方差曲线E,如图7a~图7h所示。图8b~图8i分别是从图8a中相应的具有不正确波长(λ+Δλ)和衍射距离(d1+Δd)的解密图像。从图7中可以看出E值在正确的密钥周围急剧变化,从解密的图中看不到原始彩色图像的任何信息,这意味着本文中提出的加密系统有着高度安全性。公式如下:
(10)
式中,Y(x,y)和X(x,y)表示位置(x,y)处的恢复图像和原始图像的像素值,M和N分别表示图像的高度和宽度。
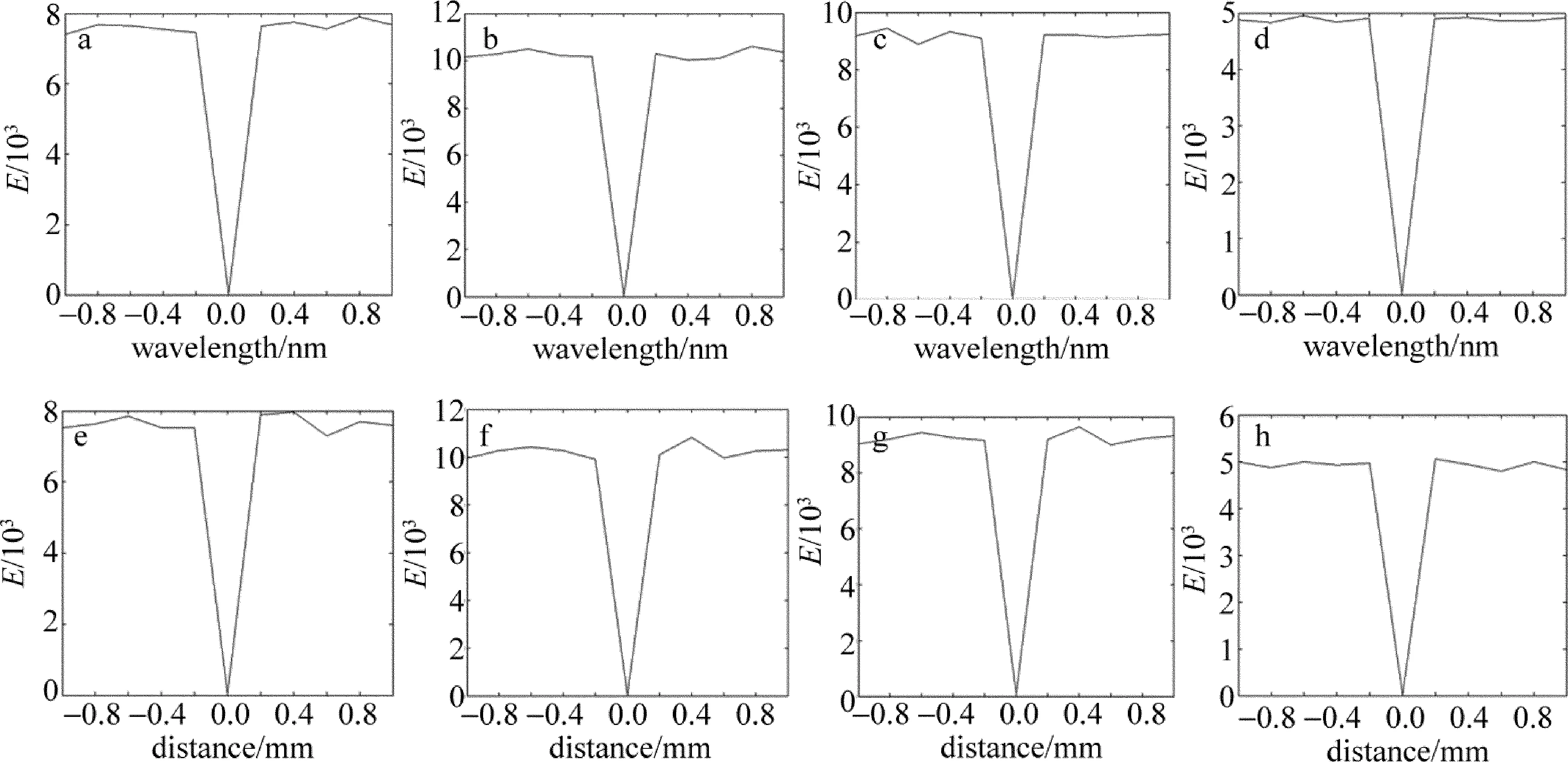
Fig.7 E curves of the decrypted color imagesa~d—for λ+Δλ(Δλ=20nm) e~h—for d1+Δd(Δd=20mm)

Fig.8 Results of incorrect phase mask key
a—the encrypted color cipher textI(μ,ν) be—withλ+Δλ(Δλ=20nm) fi—withd1+Δd(Δd=20mm)
2.3.1 抗噪性能分析 在图像存储和传输中,密文图像不可避免地受到噪声污染以及数据的丢失。因此,需要通过考虑加密图像中的椒盐噪声来测试所提出的抗噪声攻击的能力。按照参量k调整不同强度的椒盐噪声,如下所示:
I′=I(1+kG)
(11)
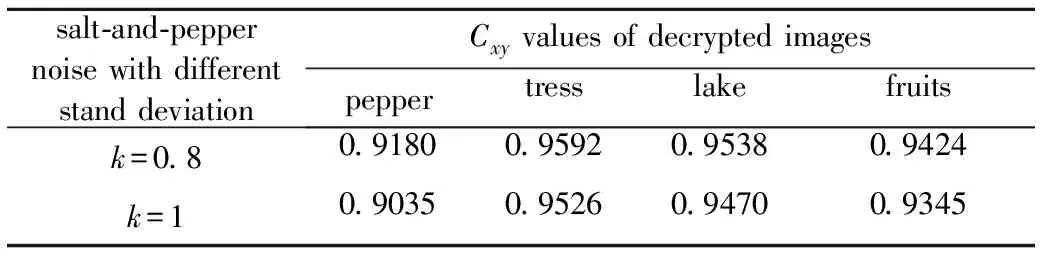
Table 2 Cxy values of the decrypted images after noise

Fig.9 The restored images after adding the salt-and-pepper noisea~d—k=0.8 e~h—k=1
式中,I′表示受噪声影响的加密图像,k是表示噪声强度的系数,G是椒盐噪声。恢复的图像如图9a~图9h所示。Cxy值如表2所示。从解密图像中几乎可以完全看到原始彩色图像的信息。可以得出结论,本文中的方法有很好的抗噪声攻击的能力。
2.3.2 抗裁剪性能分析 本加密方案的鲁棒性是通过遮挡攻击来分析的。图10a和图10f分别是加密数据被遮挡25%和50%的图,其解密图像分别如图10b~图10j。表3为解密图像的Cxy值。可以看出,本文中提出的加密系统对于遮挡攻击具有一定的鲁棒性。

Table 3 Cxy values of the corresponding decrypted images after occlusion

Fig.10 Robustness against occlusion attack
a—50% occlusion of the encrypted data b~e—the corresponding recovered images from Fig.10a f—25% occlusion of the encrypted data g~j—the corresponding recovered images from Fig.10f
3 结 论
设计了一种基于小波变换和菲涅耳变换的多彩色图像加密算法,能有效的解决多彩色图像加密后数据量大,传输速度慢的问题。本文中提出的方法不仅可以增加加密图像的容量,而且可以减少加密通道,大大降低加密系统的复杂度。该算法具有灵活性高、密钥敏感性强,且能有效抵抗分析攻击和统计分析等特点。
