GH4037镍基高温合金激光打孔相变过程数值模拟
2018-11-23王琪琪任乃飞任旭东
王琪琪,任乃飞,任旭东
(江苏大学 机械工程学院,镇江 212013)
引 言
激光打孔过程既存在熔化又存在气化蒸发,是一个复杂的多态多物理场耦合过程。国内外研究人员围绕激光参量对激光打孔质量的影响规律与激光打孔工艺参量优化已经开展了大量的实验研究[1-9],如WANG[1]等人基于单因素法的激光打孔实验,分析了激光器电压、脉冲宽度、重复频率、聚焦条件、辅助气体等对不锈钢激光打孔的影响规律。FU[2]等人利用光纤激光打孔实验分析了激光功率、占空比、切割速率、重复频率等参量对光纤激光打孔质量的影响。QIAN[3]等人基于正交实验方法进行的激光打孔实验,得出了SUS304不锈钢激光打孔的最优实验参量组合。
但是,采用传统的实验手段难以解释和分析激光打孔的机理以及激光打孔过程中材料的相变过程。采用模拟仿真的方法有利于研究激光打孔的物理机制和瞬态过程,并为实际的激光打孔加工提供理论指导。
早期针对激光打孔过程的模拟仿真主要基于解析法[10-11],如SWIFT-HOOK等人引入高斯分布的激光热源建立了激光热作用物理模型,分析了激光移动速率对熔池大小及形状的影响[10],但未考虑相变潜热的影响。WU等人以无限大均匀介质中热扩散方程的解为理论工具,给出了激光打孔过程的近似数学表达式,模拟了激光打孔的孔洞形成过程[11]。但利用解析法求解时,无法处理材料热物理参量随温度变化的实际情况[12]。
目前,针对激光打孔过程的数值模拟主要基于热传导理论[13-17],即通过求解热传导方程得到激光打孔过程的温度场。ZHANG等人建立了1维稳态热传导模型,研究了长脉冲激光打孔的效能比,计算了不同激光能量密度下的打孔深度[13]。CHU等人基于有限元法建立了2维激光打孔模型,考虑了激光束空间分布和材料相变潜热对孔的影响,计算了激光打孔过程温度场和孔型演化过程[14]。BEGIC-HAJDAREVIC等人基于有限体积法计算了激光打孔过程中温度的分布和孔的几何形状[15]。SONG等人利用ANSYS软件中的单元生死技术对激光打孔过程的温度场进行模拟仿真,得到了小孔的孔深、孔径的时间特性以及随激光能量的变化曲线[16],但该模型忽略了打孔过程中产生的熔化现象,只考虑材料的气化。
基于热传导理论的模型大多忽略了重力、反冲压力和粘滞力等对激光打孔的影响,且仅考虑材料的固-液相变过程,忽略了材料的液-气相变过程,因此仅能模拟激光打孔过程中的温度分布情况。另外,激光打孔过程中材料发生相变会导致材料的热物理属性发生阶跃跳变,需要对随温度变化的材料参量进行平滑处理。材料的熔化和气化蒸发过程还涉及到粘滞力和反冲压力的作用,以及相变潜热和热对流的影响,因此基于热传导理论建立准确的激光打孔模型较为困难。
本文中以航空涡轮发动机叶片常用的GH4037镍基高温合金为研究对象,基于流体传热和流体力学理论建立了控制方程组,模型中考虑了重力、反冲压力和粘滞力的作用,也考虑了材料的固/液相变和气/液相变过程,提高了激光打孔模型的准确性。通过计算得到了激光打孔相变过程中不同时刻的温度场分布、熔池流动速率以及气化蒸发速率,为进一步开展激光打孔的研究奠定了理论基础。
1 数学模型
1.1 有限元模型
本文中有限元模型的建立、参量设置、边界条件设置、求解以及后处理等均基于COMSOL MULTIPHY-SICS多物理场仿真软件。为便于计算,有限元模型采用2维模型,分为上下两个矩形域。上矩形域为空气,长4mm,高4mm;下矩形域为GH4037镍基高温合金,长4mm,高1mm。考虑到模型精确性,同时减少计算量,在空气以及材料表面以下0.5mm左右的深度构造较细的网格,其它区域构建较粗的网格,网格类型采用三角形网格。几何模型的网格划分效果如图1所示。
1.2 控制方程
假设激光打孔过程中主要受到重力、粘滞力和反冲压力的作用,熔化和气化材料的传热过程主要受到热传导和热对流的作用。根据质量守恒、动量守恒和能量守恒原则,给出气、液、固三相统一的控制方程如下:
▽(ρu)=0
(1)

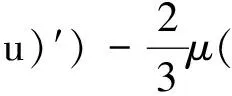
(2)

(3)
式中,ρ为密度,u为速度矢量,p为压强,μ为动态粘度,g为重力加速度,T为绝对温度,cp为比定压热容,κ为热导率,S(x,t)为热源项。
激光热源采用高斯面热源模型,热源项的数学表达式如下:
(4)
式中,激光功率P=2000W,反射率R=0.74,光斑半径r=0.25mm。
1.3 初始条件和边界条件
(1)初始值速率u=0m/s,压力p=1×105Pa,T为环境温度,则有T=300K。
(2)温度边界条件设置为绝热,边界方程为:
-κ·▽T=0
(5)
(3)速度边界条件设置为无滑移边界,边界方程为:
u=0
(6)
1.4 空气与GH4037镍基高温合金物理参量
空气的热物理属性[18]如表1所示。

Table 1 Physical properties of air
随温度变化的空气密度ρ可由以下表达式计算:
ρ=p·M/(α·T)
(7)
式中,空气摩尔质量M=0.0289kg/mol,通用气体常数α=8.314J/(mol·K)。
GH4037镍基高温合金的热物理属性[19]如表2所示。

Table 2 Physical properties of GH4037 Nickel-based superalloy
采用等效热熔法处理材料熔化和气化过程的相变潜热的影响,等效热熔法的表达式如下[20]:

(8)

(9)

(10)
式中,H((T-Tm),ΔT)和H((T-Tv),ΔT)均为Hea-viside平滑函数,分别用于处理材料在固-液相变和液-气相变过程中的相变潜热;δm和δv为高斯函数,高斯函数的中心分别为材料的熔点和沸点;ΔT为相转变温度范围,本文中取ΔT=50K。
在材料发生固-液相变和液-气相变过程中,材料的密度ρ也会发生两次阶跃性跳变,容易导致求解过程出现奇异。本文中也采用Heaviside平滑函数对其进行处理,改善了模型的收敛性。经平滑处理后的GH4037镍基高温合金的密度ρ如图2所示。

Fig.2 Density of GH4037 Nickel-based superalloy after smoothing
2 模拟结果与分析
2.1 温度场模拟结果
图3为激光作用0.80ms,1.20ms,1.60ms和1.70ms左右的温度场模拟结果。图3中的横纵坐标分别代表几何区域的长和高,单位为mm,色柱表示温度,单位为K。如图3a、图3b所示,在激光加热早期阶段,激光束主要用于加热基体,激光束下方的材料达到融化温度后,开始形成小的熔池,此时激光能量以菲涅尔吸收的方式被材料表面吸收,其余能量被反射,传热过程以热传导方式为主。随着加热时间增加,热传导现象加剧,熔池的深度随之增加。如图3c所示,激光加热1.60ms左右,材料表面发生气化现象,在小孔内外压力差的作用下,气化材料沿垂直方向向上喷出,并与周围空气形成了热对流。如图3d所示,激光加热1.70ms左右,材料气化蒸发现象更加明显,气化后的材料进一步上升,并向周围扩散,形成了类似“蘑菇云”的形状。

Fig.3 Simulation results of temperature fielda—t=0.80ms b—t=1.20ms c—t=1.60ms d—t=1.70ms
2.2 速度场模拟结果
图4a、图4b分别为熔池表面和熔池内部不同位置(x,y)的水平流动速率。从图4a可以看出,熔池中心区域的水平流动速率较快,两端的水平流动速率较慢,水平流动速率最高为1.7m/s。从图4b可以看出,熔池表面的水平速率较高,越往下水平速率越低。

Fig.4 Horizontal flow velocity of molten poola—surface b—inside
结合图4a、图4b可以看出,在激光加热早期阶段,熔池表面和内部的水平流动速率都较低,随着激光作用时间增加,熔池表面和内部的水平流动速率开始增加,但增速均较为缓慢。在激光加热1.70ms左右,熔池表面和内部的水平流动速率都迅速上升。
图5为熔池表面的垂直流动速率。从中可以看出,在激光加热0.50ms左右,熔池开始出现垂直流动。随着时间的增加,熔池的垂直流动速率不断增加,在激光加热1.70ms左右,熔池的垂直速率也迅速上升。从图5中还能看出,靠近熔池中心区域的垂直流动速率较快,熔池两端的垂直流动速率较慢,垂直流动速率最高为1.1m/s。

Fig.5 Vertical flow velocity at the surface of molten pool
图6为材料表面不同位置的压力随时间变化的曲线。从图6可以看出,在激光加热初始阶段,此时的压力与大气压力相同,然后随着激光加热时间增加,压力开始缓慢的上升,在激光加热1.70ms左右,压力开始迅速上升,中心点压力最大达到1.38×105Pa,而且距离中心区域越近最大压力越大。
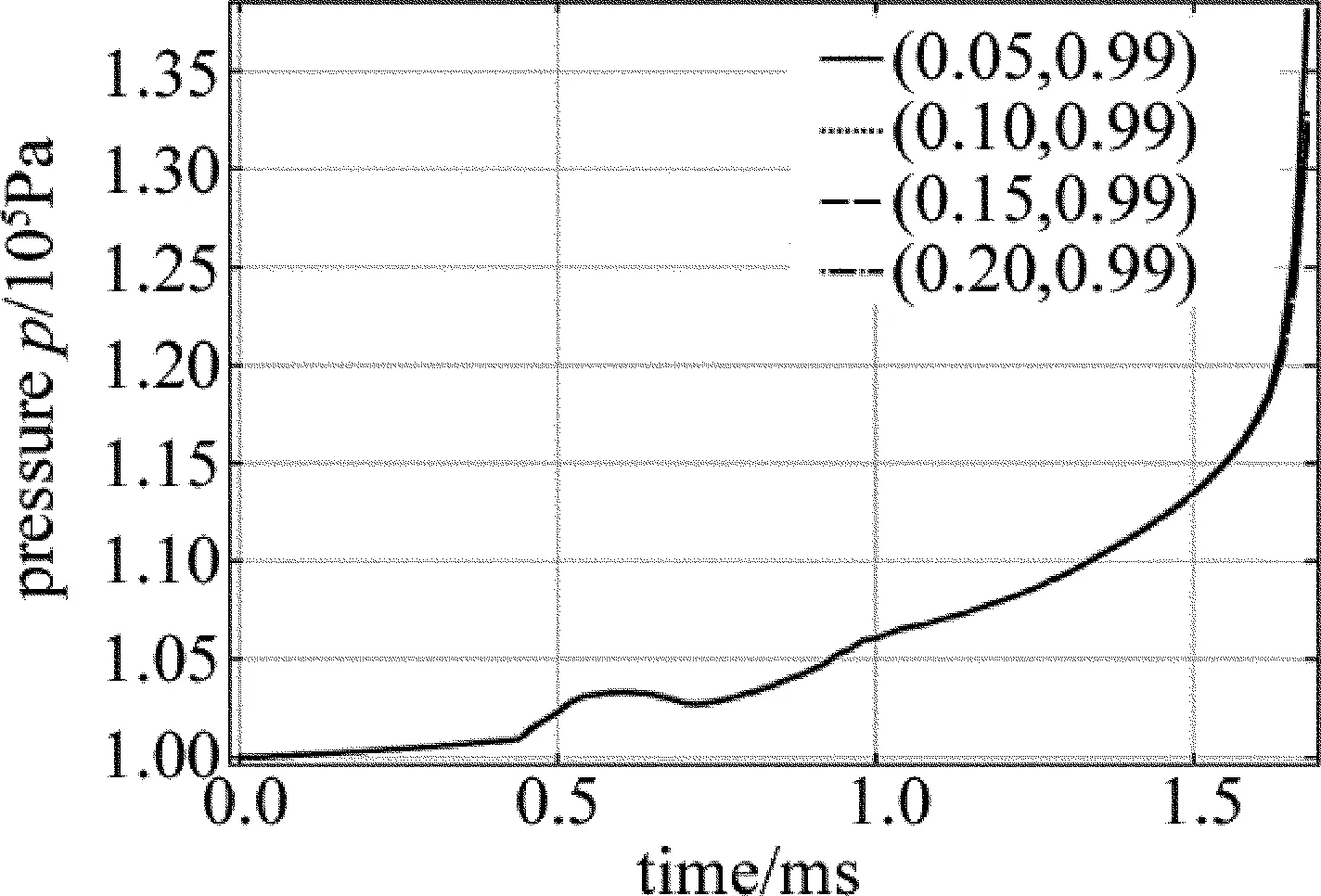
Fig.6 Pressure at the surface of molten pool
对比熔池水平和垂直流动速率与压力的模拟结果可以看出,在激光加热1.70ms左右压力迅速上升,距离中心点越近最大压力越大,此时速率场模拟中的熔池流速也在迅速上升,且越靠近熔池中心区域流动速率较快,表明蒸发气体的反冲压力可以加快熔池的流动。
图7为激光作用1.60ms,1.64ms,1.66ms和1.70ms时的材料气化蒸发速率场模拟结果。图中的横纵坐标分别代表几何区域的长和高,单位为mm,色柱表示速率,单位为m/s。从图上可以看出,在材料发生气化后,材料的最大气化蒸发速率由1.60ms时的35m/s迅速增加到1.70ms时的250m/s。靠近材料表面中心区域的材料蒸发速率最高,向周围扩散的气化蒸发材料在空气的阻力作用下速率逐渐递减。

Fig.7 Simulation results of vertical fielda—t=1.60ms b—t=1.64ms c—t=1.66ms d—t=1.70ms
3 结 论
基于流体力学和流体传热理论建立了GH4037镍基高温合金激光打孔相变模型,计算了激光打孔相变过程的温度场分布、熔池流动速率以及气化蒸发速率,模拟结果较好地展示了材料熔化和气化蒸发的相变过程。
(1)随着激光作用时间增加,材料相继发生熔化和气化现象,熔化材料初期在粘滞力和重力的阻碍作用下流动较为缓慢,然后在气化蒸发材料的反冲压力下,熔池的流动速率迅速增加,气化蒸发材料沿垂直方向从小孔喷射到空气中,并向周围空气中扩散。
(2)在激光功率为2000W、脉宽为1.70ms时,熔池的水平流动最高速率为1.7m/s,垂直流动最高速率为1.1m/s,材料最大气化蒸发速率可以达到250m/s。
