保温混凝土细观模型建立及导热系数分析
2018-11-23王绎景秦渊王文婧李珠
王绎景 ,秦渊 ,王文婧 ,李珠
(1.太原理工大学 土木与建筑工程学院,山西 太原 030024;2.阳光凯迪新能源集团有限公司,湖北 武汉 430223)
0 引言
混凝土作为一种多相非均质材料,在宏观层次对其进行力学与导热分析,无法准确描述混凝土非均质的特点。混凝土计算力学经过几十年的发展,已经从宏观发展到细观,对混凝土理论发展做出了巨大贡献。从细观尺度来看,混凝土是由离散相的粗骨料,连续相的砂浆基质与两者间界面过渡区组成的三相非均质材料,对于这一特点,基于损伤原理的微平面模型[1]、基于物理学的网格模型[2]以及基于混凝土细观结构的随机粒子模型[3]相继被建立,在混凝土细观力学发展过程中发挥出巨大的作用。王宗敏等[4]基于随机粒子模型提出了随机骨料模型,将混凝土粗骨料用随机数的原理进行投放,并对混凝土轴心受压进行数值模拟。张伟平等[5]使用圆形随机骨料模型,对混凝土导热进行了数值模拟,验证其有效性,分析粗骨料随机分布对混凝土导热系数的影响。同年,Zhang L等[6]利用泰森多边形建立起三维沥青混合料随机骨料模型,通过对模型进行稳态导热数值模拟,验证了沥青混凝土数值模拟的有效性。
玻化微珠保温混凝土是在普通承重混凝土中加入一定比例的玻化微珠替代部分细骨料,使混凝土具有了保温的功能[7]。随后,王文婧等[8-9]对保温混凝土的力学与保温性能进行了大量研究。
本文将玻化微珠保温混凝土这种新型材料与细观模型结合起来,通过随机生成与投放粗骨料和保温细骨料,建立保温混凝土细观模型,验证其有效性。对圆形、椭圆形和多边形这3种不同形状粗骨料的混凝土细观模型进行导热分析,研究粗骨料形状对混凝土导热性能的影响。
1 细观模型建立
1.1 理论基础
由于混凝土的界面过渡区中存在大量的微裂缝与微孔隙,使得混凝土粗骨料与砂浆之间存在界面热阻,使其导热系数降低。在本研究中暂不考虑界面热阻,可以将混凝土看作离散相与连续相的两相复合材料,其中离散相为粗骨料与保温骨料,连续相是砂浆基质。为了模拟混凝土真实的投放过程,采用蒙特卡罗随机分布的原理进行投放。对于2种骨料在混凝土中的面积占比,采用真实级配曲线来确定。刘国权等[10]提出三维试件任意一个二维截面上粗骨料的面积占比是三维粗骨料体积占比的无偏估计。因此二维细观模型中粗骨料占比采用真实级配曲线保证了模拟的精度。
1.2 技术路线
技术路线见图1。二维细观模型是模拟混凝土试件二维随机断面,要从混凝土试件中获取有效数据,包括试件尺寸、粗骨料与保温骨料在混凝土中所占体积分数和2种骨料在混凝土中的粒径与级配曲线。随后进行建模操作并进行有限元计算,同时反映混凝土的导热性能。

图1 技术路线
1.3 随机粗骨料生成
粗骨料选用5~20 mm连续级配的石子,粗骨料级配曲线如图2所示。投放比例如表1所示。当程序判断骨料在某个级配时,骨料生成程序开始运行。为防止在程序运行时粒径较大骨料投放失败、并提高投放效率,骨料投放应按照先大后小的规律进行。
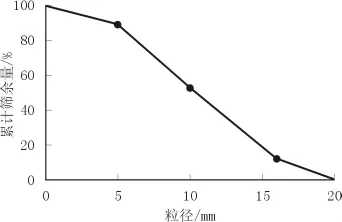
图2 石子级配曲线

表1 粗骨料投放比例
1.3.1 圆形随机骨料生成
圆形骨料示意如图3(a)所示。圆形粗骨料特征参数有3个:分别为 x0、y0、r,其中 x0、y0代表圆心坐标,r为圆的半径。生成方式均用蒙特卡罗方法实现,在程序中具体体现是使用rand(1)函数,生成一个0~1之间的随机数。具体见式(1)~式(3):
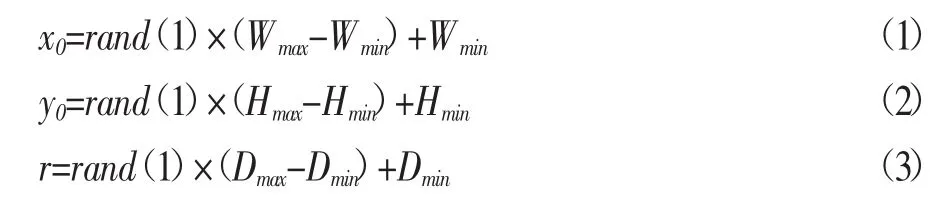
式中:Wmax、Wmin、Hmax和Hmin分别为混凝土试件最大与最小宽与高,Dmax与Dmin为该级配粒径的最大和取小值。

1.3.2 椭圆形随机骨料生成
椭圆形随机骨料示意如3(b)所示。它的特征参数有5个:x0、y0为椭圆形圆心坐标,a、b为椭圆的长轴与短轴,α为椭圆绕x轴与y轴旋转的角度。使用蒙特卡罗随机数生成椭圆形随机骨料。具体见式(4)~式(8):

1.3.3 随机顶点多边形骨料生成
宋晓刚和杨智春[11]提出一种多边形骨料的生成方式,利用这种方式可以快速生成大量随机多边形骨料。多边形骨料生成示意如图3(c)所示。生成时首先要生成半径为R的基圆。在基圆内部随机生成多边形的顶点,基圆圆心为x0、y0,多边形顶点坐标为xi、yi。顶点与圆心连线与x轴的角度αi称为顶点的角度,ri为顶点与圆心的距离,其数值不大于基圆半径。多边形骨料生成随机数目的顶点。角度αi随着顶点的生成不停增长,当αk>2π时,停止顶点的生成。顶点的数量为n=k-1。该程序可以随机生成顶点数目为4~6的多边形骨料。具体见式(9)~式(16):
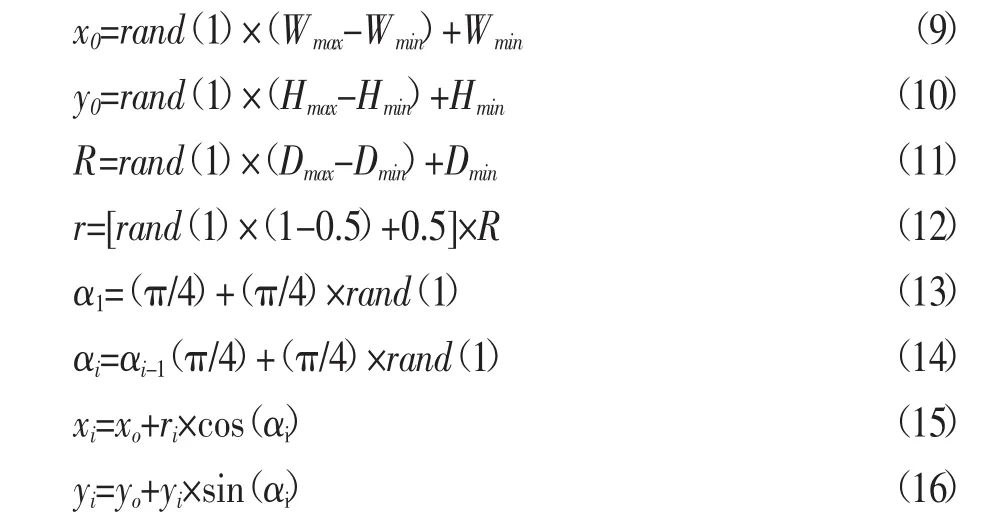
1.4 随机粗骨料干涉判断
1.4.1 圆形骨料干涉判断
对于圆形骨料,由于骨料形状比较标准,在判断时只需将两骨料圆心间距离与两骨料半径之和比较即可,当骨料距离大于半径和时,两骨料判断为相离。即:
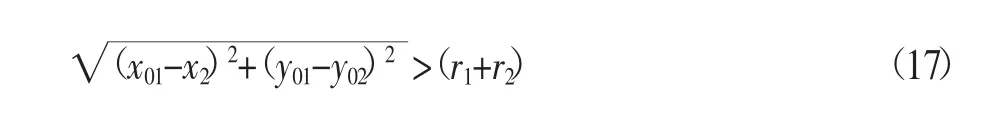
1.4.2 椭圆形骨料干涉判断
刘洋和申立勇[12]给出了在计算机图形学领域2个椭圆位置关系的代数条件。假设椭圆A与椭圆B用二次型的形式表示:A:XtAX<0和 B:XtBX<0。所以 2个椭圆的广义特征多相式为:f(λ)=det(λA+B)。若f(λ)=0存在2个相异正根,则判定2个椭圆分离。对于每一个骨料进行判定,若没有发生干涉,则将数据储存。
1.4.3 多边形随机骨料干涉判断
为提高运算效率,对于多边形随机骨料,采用布尔运算来进行干涉判断。布尔运算是数字符号化的逻辑推演法,包括联合、相交、相减。在程序中,使用相交算法进行运算。将新生成的多边形骨料与既有多边形骨料进行相交,并计算相交面积,当相交面积等于0时两骨料分离,判定为不相交,反之则判定为干涉。在商用软件MATLAB中,polyarea函数可对布尔运算相交面积进行计算。对之前生成的每一个骨料均进行干涉判断,若均无发生干涉则将骨料数据以矩阵形式储存。将粗骨料投放结束之后,生成的二维细观模型如图4所示。
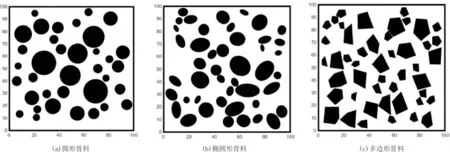
图4 混凝土的细观模型(粗骨料30%)
1.5 随机保温骨料生成与干涉判断
粗骨料投放结束后,按照先大后小的规律进行保温骨料的投放。保温骨料选用0.5~2.0 mm连续级配的玻化微珠,其级配曲线如图5所示。考虑到0.315 mm以下的玻化微珠数量及尺寸过小,建模较为复杂,将玻化微珠级配进行调整。王文婧等[13]通过对再生保温混凝土切片进行图像分析,发现由于搅拌过程中玻化微珠发生一定的破碎,试件中玻化微珠级配发生很大改变。对玻化微珠投放比例进行调整,调整后投放比例见表2。玻化微珠由于其数量巨大,投放困难,为了简化计算并提高投放效率,选用圆形来进行表示。骨料生成方式 与1.3.1一致,详细见式(1)~式(3)。由于粗骨料种类不同,保温骨料与不同形状的粗骨料干涉条件也不同,参考前文1.4节中的内容来进行骨料干涉判断。
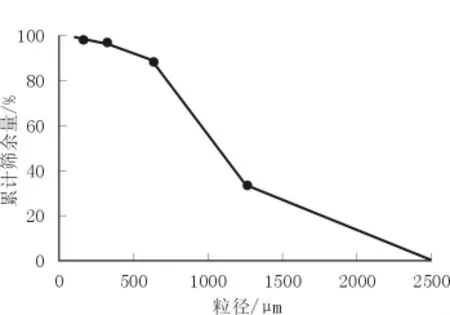
图5 玻化微珠的级配曲线
在进行骨料干涉时,不仅要与生成的粗骨料进行依次判定,还要与已生成保温骨料依次进行干涉判定,当且仅当均无发生碰撞时,保温骨料才可进行投放。当所有骨料投放结束后,保温混凝土二维细观模型如图6所示。

表2 保温骨料投放比例
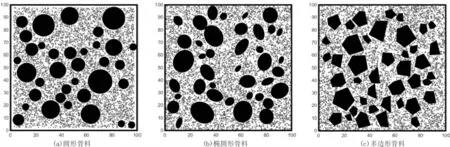
图6 保温混凝土细观模型(粗骨料30%,玻化微珠10%)
2 稳态导热分析
2.1 有限元模型建立
二维细观模型建立后,建立有限元模型并进行稳态导热分析。由于保温骨料数量巨大且尺寸较小,对其利用传统有限元方法建模并划分网格显然会消耗大量资源,且计算机利用率不高。对于此种情况采用背景网格方法对其进行建模与划分网格处理。背景网格法是将混凝土试件范围划分为等面积、排列整齐的有限元单元,将它作为背景网格。将混凝土二维模型投影到背景网格中,通过程序判断不同材料在背景网格中的有限元坐标,并对背景网格单元分别赋予材料属性,即可完成对混凝土细观有限元模型的网格划分。刘婷[14]使用背景网格法对有限元网格自动划分;唐欣薇和张楚汉[15]提出使用状态矩阵法对细观模型进行骨料干涉判断与有限元模型自动剖分。
基于图像数字化处理的方法,本研究提出了一种改进背景网格建立方式。
(1)首先应确定背景网格尺寸。混凝土试件模型中最小的单元为玻化微珠,基于级配限制其最小直径为0.315 mm。为了保证有限元计算的准确性确定有限元单元尺寸为0.1 mm×0.1 mm,由于试件尺寸为100 mm×100 mm,所以单元数量为106。
(2)二维细观模型不同组分材料输出为不同颜色,并对同一种材料颜色进行统一,例如粗骨料为黑色、砂浆层为白色,保温骨料为绿色。将二维细观模型输出为图片,并利用图形处理软件对图形进行处理。将图片分辨率设置为1000×1000,并对其进行色调分离处理,增强边界效果,防止有限元模型不连续。
(3)提取处理后图片颜色信息,采用RGB图像模式,黑色RGB 数值为(0,0,0)、白色为(255,255,255)、绿色为(0,255,0)。生成 1000×1000 矩阵 M(1000,1000),矩阵中每个元素初始化设置为1。当某个位置像素RGB数值之和大于255时,对应矩阵位置上数值M(i,j)=1,定义为砂浆区;当该位置像素RGB数值之和等于 255时,对应矩阵位置上数值 M(i,j)=2,定义为保温骨料区;当该位置像素RGB之和等于0时,对应矩阵位置上数值 M(i,j)=0,定义为粗骨料区。
(4)在有限元程序中生成106个排列整齐的有限元单元后,将矩阵 M(1000,1000)输入程序,并依据 M(i,j)数值对单元依次赋予材料属性,至此有限元模型建立完毕。保温混凝土有限元模型见图7所示。
2.2 稳态导热系数分析
在模拟试验中,模拟混凝土的稳态导热现象。荷载加载如图8所示,上边设为混凝土的热侧,温度设置为35℃。下边设为混凝土的冷测,温度设置为15℃。两侧设定为绝热。稳态导热形成的温度场为稳态温度场,即温度场中各点的温度不随时间的变化而改变。由于是稳态导热现象,流入与流出试件的热量相等。

图7 保温混凝土背景网格有限元模型
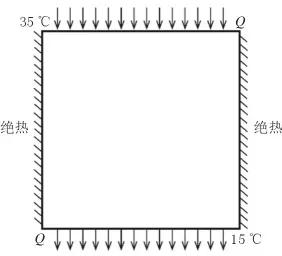
图8 模拟试件荷载示意
傅里叶定律[式(18)]是稳态导热的基础,其含义为在导热现象中,单位时间内通过给定截面的热量,正比例于垂直于该截面方向上的温度变化率于截面面积,而热量传递的方向则与温度升高的方向相反。

在模拟试验中,通过有限元计算可获得通过混凝土试件的总热量Q,并通过计算来获得试件的导热系数。
2.3 有效性分析
粗骨料占比通过配合比计算与数字化图片处理综合分析,确定为30%。
为了获取较为准确的试验数据,对于保温骨料的面积占比采用2种方法计算:
(1)利用王文婧等[13]的研究方法,通过对混凝土切片进行图片数字化处理,获取再生保温混凝土中各组分材料面积占比。分析得粗骨料占混凝土的30%,玻化微珠占混凝土的10%。
(2)通过试验法获取保温骨料面积占比。试配20 L玻化微珠保温混凝土,记录材料用量并准确测试混凝土体积V1,除配合比中玻化微珠用量,控制别的变量保持不变,采用同样材料用量,相同工艺适配混凝土,准确测试混凝土体积V2。按式(19)计算玻化微珠占比γ。

通过试验得,玻化微珠占混凝土的28%。
各组分材料导热系数按表3选用。课题组利用传热试验推算保温混凝土的导热系数为0.412 W/(m·K)。

表3 各组分材料导热系数
当玻化微珠投放量分别为0、10%及28%时,混凝土的导热系数如图9所示。当没有投放玻化微珠时,圆形粗骨料导热系数计算为2.043 W/(m·K);当玻化微珠投放量分别为10%、28%时,混凝土的导热系数分别为1.412、0.423 W/(m·K),分别降低了30.88%与79.3%。结果表明,当玻化微珠投放量为10%时,数值混凝土试件的导热系数与真实混凝土相差较大,误差为223.9%。可能是由于玻化微珠强度不足,混凝土切片在制作过程经过切割、打磨,使得切片表面的玻化微珠破碎,试件表面无法准确表示出玻化微珠真实的数量。采用试验法进行保温骨料体积占比计算时,可以排除玻化微珠在搅拌过程中破碎因素,有效并准确地确定保温骨料的体积占比,数值混凝土导热系数的误差为2.67%。
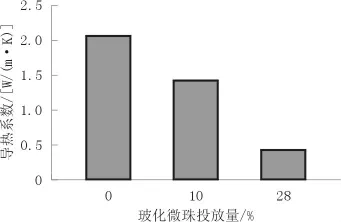
图9 数值混凝土在不同玻化微珠投放量时的导热系数
2.4 粗骨料形状对保温混凝土导热系数的影响
不同形状粗骨料的数值混凝土在玻化微珠不同投放量下的导热系数变化如图10所示。
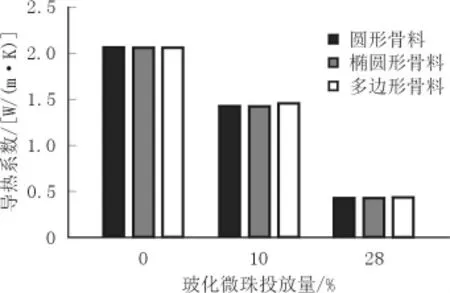
图10 粗骨料形状对保温混凝土导热系数的影响
由图10可见,在数值模拟中,粗骨料形状对混凝土导热系数影响较小,且存在规律:当粗骨料形状为多边形时,其导热系数为三者中最大,椭圆形骨料次之,圆形骨料最小。但由于在保温混凝土中玻化微珠投放成为导热系数降低的主要因素,粗骨料形状对混凝土有效导热系数的影响相对较小。
3 结论与展望
(1)建立的保温混凝土细观模型可较准确地描述混凝土粗骨料与保温骨料数量,级配等参数。并能够模拟混凝土试件制作过程中的随机性与不确定性。
(2)提出的基于数字化图片处理背景网格建立方法能较好地适用于含有大量颗粒非均质的混凝土细观模型,节省有限元建模时间,提高建模效率。
(3)玻化微珠保温混凝土细观模型能够有效地模拟混凝土的导热系数,且误差较小。
(4)在数值模拟中粗骨料形状对混凝土导热系数影响较小。
