基于概率积分法的采动坡体稳定性预测与分析

王猛，孙丽丽，薄怀志

(1.山东省地质矿产勘查开发局第二地质大队，山东 济宁 272000；2.山东省地矿局采煤塌陷地综合治理工程技术研究中心，山东 济宁 272000；3.兖州煤业股份有限公司 兴隆庄煤矿，山东 济宁 272000;4.山东省地质矿产勘查开发局第三水文地质工程地质大队，山东 济宁 272000)

0 引言

地下采煤会对土地结构和地质环境造成严重损害[1]，滑坡是采动损害的主要形式之一，给人们的生命财产和经济建设造成重大损失[2]。因此,采动坡体的稳定性分析评价一直是地下采矿工程中实际关心的问题。

目前，常用的坡体稳定性预测方法有极限平衡法、工程地质类比法、数值分析法、神经网络、模糊数学、可靠度理论等[3-10]。基于极限平衡法的采动坡体稳定性预测方法力学模型简单，已应用于大量的工程实践中，并积累了丰富的实际经验，而且有依据规范的指导，应用最为广泛。但是，该方法需要地表稳态、动态移动变形量作为计算参数，且计算公式较为复杂，人工计算繁琐且容易出错，难以对坡体稳定性变化过程进行详细分析。针对这种情况，该文提出了使用概率积分法结合Knothe时间函数对地表变形值进行稳态、动态预测，然后通过极限平衡理论对坡体稳定性进行预测的方法，并介绍了采动坡体稳定性预测程序的设计和实现方法。最后，通过一个工程实例对采动引起的坡体移动变形及坡体稳定性变化情况进行了预测和分析。

1 概率积分法地表移动变形稳态、动态预测模型

根据地表移动变形预计方法的建立途径，可以将其分为3类：基于实测资料的经验法、理论模拟法和影响函数法[11]。目前，在我国普遍采用的开采沉陷预计方法是概率积分法，概率积分法是影响函数法的一种，经过我国采矿沉陷工作者20多年的研究，该方法已成为国内较为成熟、应用最为广泛的地表移动变形预测方法。

对于水平煤层或缓倾斜煤层，概率积分法地表移动变形稳态预测公式为[12]：

(1)

(2)

W(x,y)·cotθ0

(3)

式中：W(x，y)为地表任意点(坐标为x，y)的下沉值，mm；Ux(x,y),Uy(x,y)分别为地表任意一点沿x,y方向的水平移动值，mm；x,y为地面预计点坐标；Wcm为充分采动条件下地表最大下沉值，mm；Ucm为充分采动条件下地表最大水平移动值，mm；r为主要影响半径，m；u，v为开采单元在x，y方向上的坐标值，m；θ0为开采影响传播角，°；D为开采区域几何范围。地表倾斜、水平变形值可通过分别对下沉、水平移动值求一阶偏导的方法获得，即：

(4)

式中：ix(x,y),iy(x,y)分别为地表点沿x，y方向的倾斜变形值，mm/m；εx,εy分别为地表点沿x，y方向的水平变形值，mm/m。

地表移动变形的动态变化过程可以使用含有时间变量的函数表示，研究表明[13-17]，Knothe时间函数可以准确描述地表移动变形的动态过程。描述地表移动变形动态变化过程的Knothe时间函数可表示为[17]：

φ(t)=1-e-at

(5)

式中:a为与采矿地质条件有关的时间因素影响系数；t为预计时刻与工作面停采时刻之间的时间间隔，a。使用概率积分法对地表任一点(x,y)在t时刻的变形值进行动态预测的公式(6)可表示为：

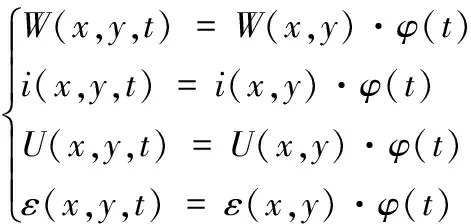
(6)

式中：W(x,y),i(x,y),U(x,y),ε(x,y)分别为使用概率积分法预测的地表稳态下沉、倾斜、水平移动及水平变形值。

2 坡体稳定性预测模型

极限平衡法是根据斜坡上的滑体或滑块的力学平衡原理(即静力平衡原理)分析斜坡各种破坏模式下的受力状态，以及斜坡上的抗滑力与下滑力之间的关系来评价斜坡的稳定性[18]。该方法以摩尔—库仑的抗剪强度理论为基础，将滑坡体划分为若干垂直土(岩)条，通过建立作用在这些垂直土(岩)条上的力的平衡方程式来求解滑坡体安全系数。

基于极限平衡理论的采动坡体稳定性计算示意图(图1)所示，AD为滑坡体主剖面上的滑动面长度L1(m);CD为滑体后壁张开性裂缝深度L2(m);α为坡面倾角；β为滑面倾角；W为ABCD所围成区域的滑动体重量(kN)；H为坡体至地表面的垂高；H0为坡体下方平均开采深度(m)；L为坡体下方开采宽度(m)；M为坡体下方煤层开采厚度(m)；Hi为坡顶至开采煤层底板垂高(m)。

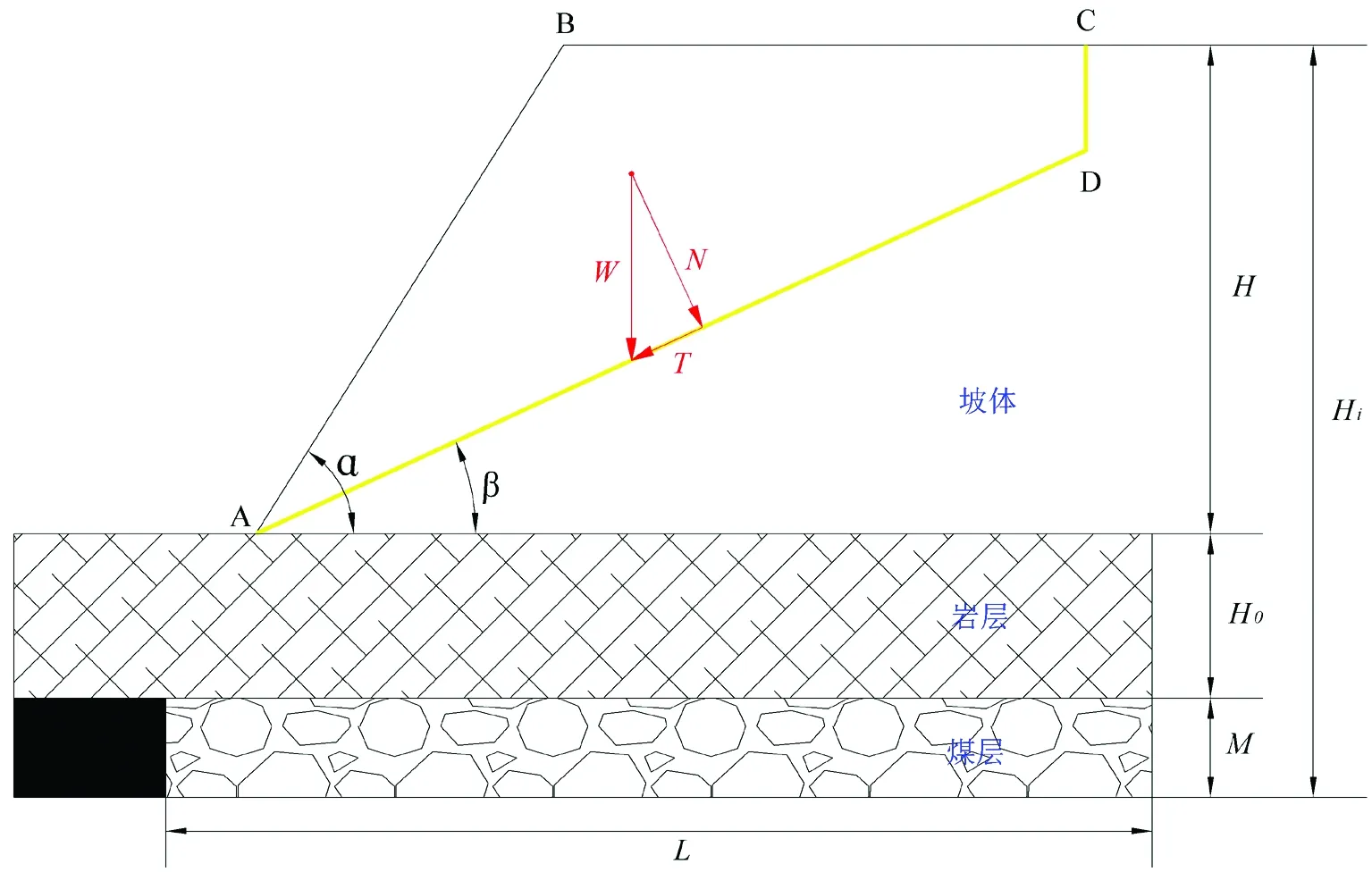
图1 单滑面采动坡体计算示意图

单滑面采动坡体稳定性可以使用安全系数K(坡体稳定性评价系数)来表示，根据极限平衡理论，滑坡体安全系数K可以使用公式(7)进行计算[19]：

式中:S为坡体抗滑力(kN)；T为坡体下滑力(kN)；P为坡体采动程度；F为煤层上覆岩层的岩性系数；ω为地下煤层开采后造成的坡顶边缘下沉值(m)；η,ζ为计算系数；φ为滑面内摩擦角；λ为与坡体岩(土)性泊松比μ有关的坡体侧压力系数；ε,ε′分别为坡顶边缘最终和动态水平变形值(拉伸为正、压缩为负，动态值取正值)；i,i′分别为坡顶边缘最终和动态倾斜变形值(倾斜与坡体同向取正，反向取负)；c为滑动面内聚力(kPa)。

当坡体稳定性评价系数K>1时，地下采煤不会造成坡体失稳；当K≤1时，地下采煤会造成开采区域上方坡体失稳，可能引起滑坡等地质灾害的发生。

3 采动坡体稳定性预测方法及实现

3.1 采动坡体稳定性预测方法

从(7)式可以看出，地下采动对坡体的稳定性影响与开采区域的采矿地质条件紧密相关，不仅取决于开采宽度、开采深度、开采厚度等开采条件，也与煤层上覆岩层及坡体的岩土力学性质有关；另外还与采动过程对地表的动态影响(动态下沉、动态倾斜及动态水平变形)有关。由于采动坡体的稳定性随着采动过程的变化而变化，在对采动坡体进行稳定性评价时，要结合地表移动变形的动态变化过程对其进行分析。

根据式(1)～(4)及(6)的概率积分法稳态、动态预测模型，可以对坡体在采动过程中产生的变形值进行稳态和动态预测，将变形预测值、采动坡体稳定性相关的几何参数值(采宽、采深等)及岩土力学参数值代入式(7)即可实现采动坡体的稳定性预测。使用概率积分法对坡体稳定性预测的流程如图2所示。

图2 基于概率积分法的采动坡体稳定性预测流程图

3.2 采动坡体稳定性预测软件的设计、实现与使用

如图3所示，采动坡体稳定性预测软件整体采用了自上而下、分层设计实现的理念，每个层次都使用模块化的软件设计方法。每个模块都具有高内聚性，模块和模块之间具有低耦合性，这种模块化的设计能够降低程序执行出错率和代码占有空间，提高程序可靠性和代码复用率，同时可以降低软件更新、升级的时间成本[20]。

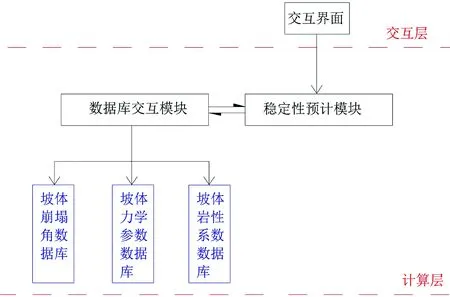
图3 软件结构设计示意图

软件结构的最顶层为交互层，该层是与用户进行交互的界面。为了方便使用，该层采用用户友好型的软件设计原则进行实现。如图4所示，该界面使用C#中的WinForm控件作为主窗体，输入参数按照预测类型、采矿地质条件、坡体地质条件使用groupBox控件分类管理，这种设计逻辑清晰，可以避免由于预计公式参数过多可能导致的输入错误问题。大部分坡体稳定性计算参数与坡体岩(土)性相关，软件将《三下采煤规程》中有关参数使用XML Schema语言构建了相关的数据库，用户可以直接选择坡体岩(土)类别，软件就能够自动选择合适的计算参数。为了使预测结果清晰、直观地展示给用户，软件采用ZedGraph绘图控件对预测结果进行展示[21]；另外还可以根据需要，将详细的结果导出为文本文件格式，从而可以为开采方案的安全性评价提供有效、翔实的科学依据。

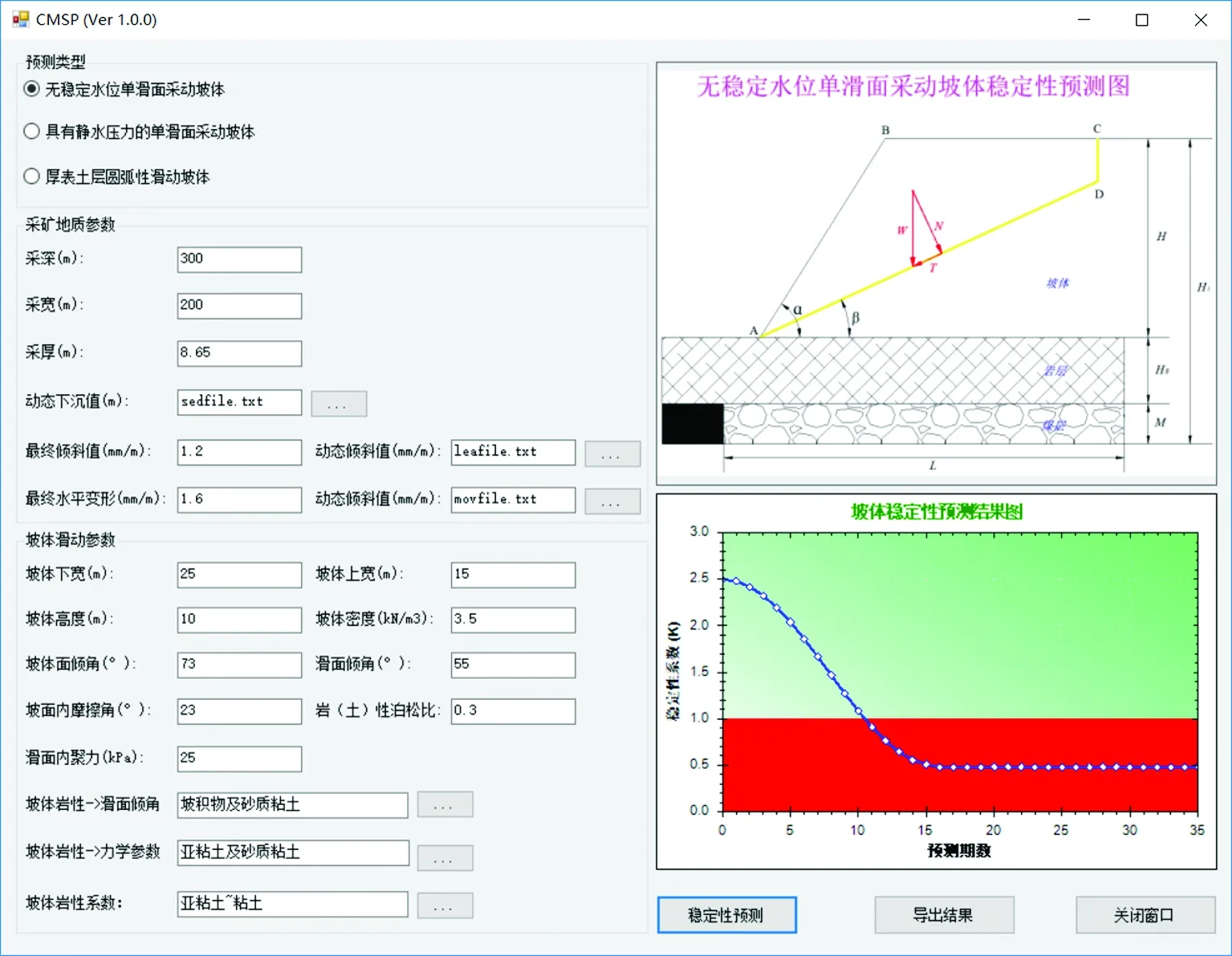
图4 采动坡体稳定性预测软件界面

坡体稳定性预测公式计算参数繁多，但大多数参数与坡体的岩(土)性质有关，通过确定坡体的岩(土)性质，即可确定大多数计算参数。部分坡体力学参数的取值如表1所示，使用XML Schema储存坡体力学参数的数据结构设计及实现如图5所示，坡体岩(土)性质作为结构的第二层子元素，力学参数作为第三层子元素，力学参数的最大、最小取值作为同级的第四层子元素；坡体力学参数的取值限定为双精度浮点型。岩(土)性质不同的坡体(如坡积物及亚粘土、亚粘土和砂质粘土)可以通过设置第二层子元素的属性来进行区别；同样，同一岩(土)性质坡体的不同力学参数通过第三次子元素的属性来进行区别。从图5可以看出，XML Schema可以结构清晰、层次鲜明地实现坡体稳定性预测计算参数的储存，结合C#提供的XML操作类可以非常简单地对相关参数进行查询、增加、删除和编辑[22]。

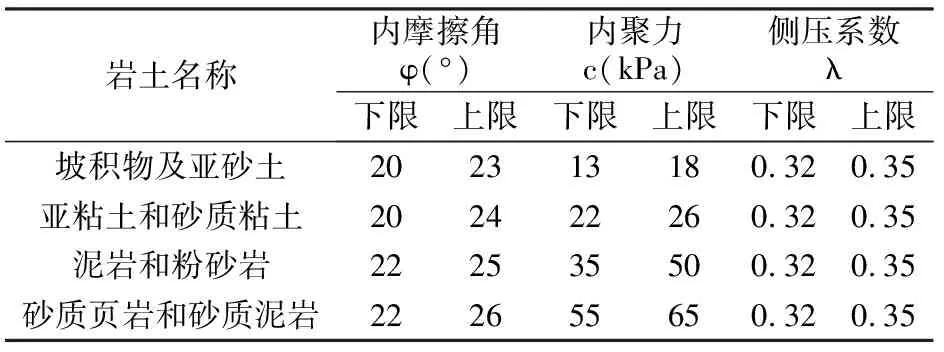
表1 坡体稳定性计算力学参数取值

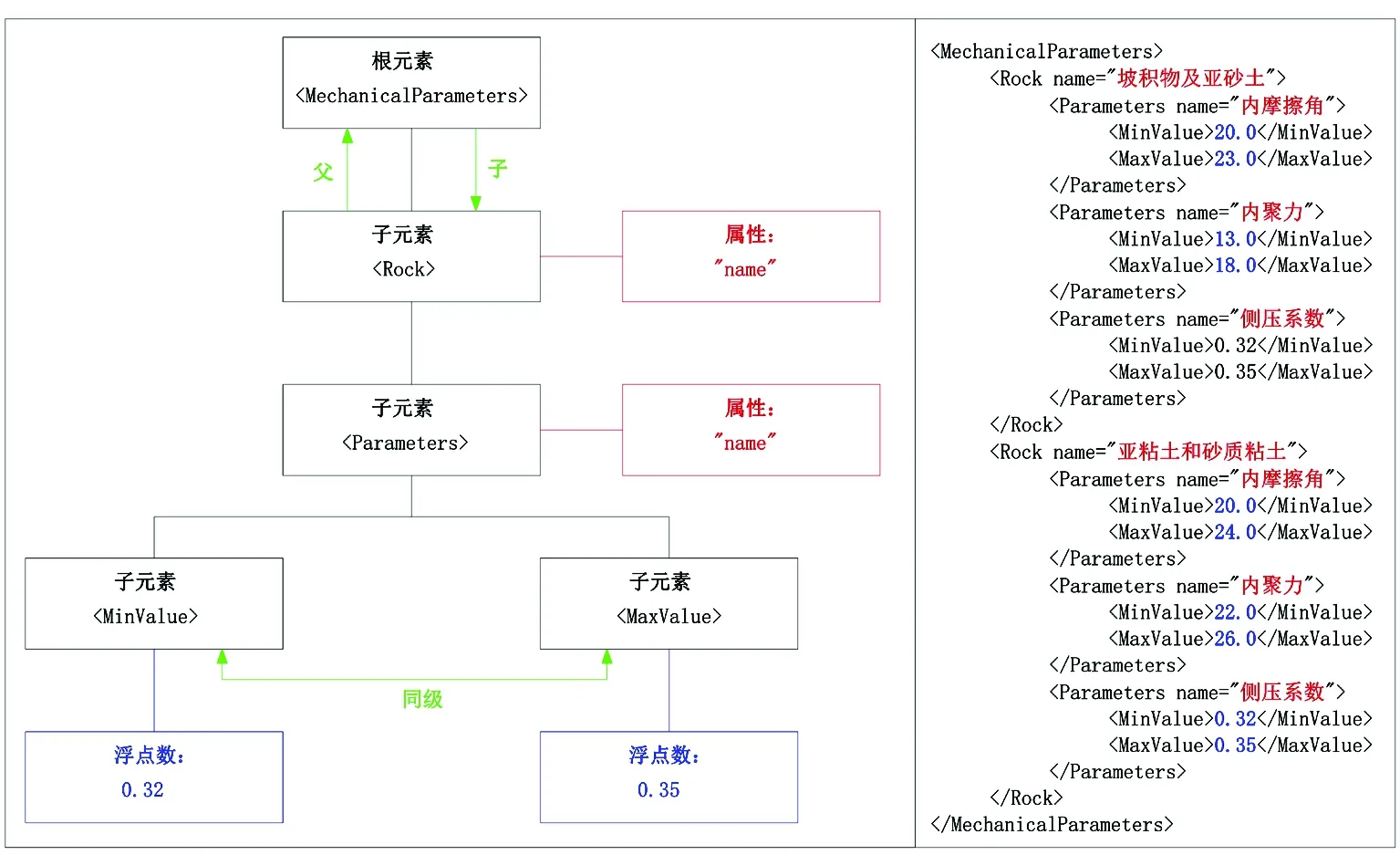
图5 坡体力学参数的XML Schema结构设计与实现

采动坡体稳定性预测软件的使用流程如下：

(1)使用概率积分法分别预测坡顶边缘的稳态及动态下沉、倾斜及水平移动值，并将预测的坡体变形值输入到预测软件中。

(2)输入工作面采宽、采长、采厚等坡体稳定性预测几何参数。

(3)选择坡体岩(土)性质，确定坡体岩性系数、坡体崩塌角等坡体稳定性预测力学参数。

(4)进行坡体稳定性预测，输出预测结果。

4 工程实例及分析

某矿1316工作面为该矿一采区北部首采工作面，工作面设计宽度170m，推进长度542m，平均采深-310m，煤层倾角3°，开采煤厚8550mm，推进速度2.5m/d；工作面回采工艺为综采放顶煤一次采全高，顶板管理方法为全部跨落法。如图6所示，工作面切眼位于河流下方，距离切眼推进方向160m处为一梯形护河河堤，河堤底宽25m，上宽20m，高度12m；河堤岩(土)性为亚粘土和砂质粘土。

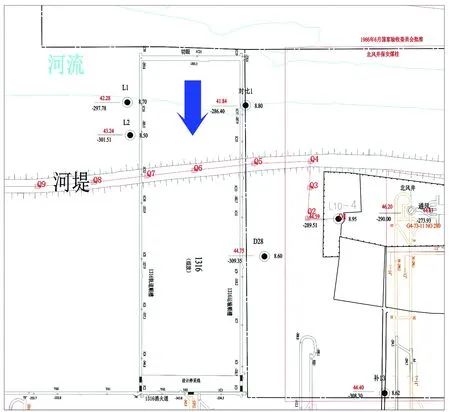
图6 工作面位置及测线布设图

为了评估该工作面采动对河堤的影响，需要在采动前对河堤稳定性进行预测；同时，该矿沿河堤方向布设了一条地表移动变形观测线(图6)，并在工作面回采期间对测线进行了17次移动变形监测。多年来，该矿已在多个采区、多个工作面布设了地表移动变形观测站，并通过实测的方法积累了丰富的岩移观测资料。通过对这些资料和相关的采矿地质条件进行回归分析确定该工作面概率积分法预测参数及Knothe时间函数系数(表2)。从工作面回采开始，每推进20m对河堤顶端移动变形值进行一次动态预测，每期动态移动变形值及最终变形值如图7所示。

可以看出，随着工作面的推进，河堤下沉值逐渐增大，最终下沉值为5959mm，由于采动滞后影响的原因[11]，下沉速度在工作面推进至河堤前方约30m处达到最大。

随着工作面由河堤后方(切眼方向)向河堤前方(停采线方向)推进，河提向采空区方向发生倾斜，当工作面推进至河堤前方约80m处时，倾斜达到最大负变形值。此后，由于河堤前方逐渐形成更大的采空区，河堤开始发生反方向倾斜(倾向停采线方向)，当河堤变形稳定后，河堤最终会发生0.4mm/m的倾斜，倾斜方向为切眼方向。

当工作面推进位置位于河堤后方(切眼方向)时，河堤水平变形值随工作面推进逐渐增加，即河提受采动影响发生拉伸；在工作面推进至河堤前方(停采线方向)约30m处时，拉伸达到最大值11.4mm/m，此后，随着河堤前方采空区的形成，河堤拉伸量逐渐减少；当工作面推进至河堤前方95m处时，河堤开始发生压缩；压缩变形随工作面的推进逐渐增大，当工作面推进至河堤150m处时，河堤达到8.2mm/m的最大压缩变形；随着工作面的继续推进，河堤压缩变形逐渐减小，当河堤变形稳定后，河堤最终会发生0.2mm/m的拉伸变形。

表2 概率积分法预测参数

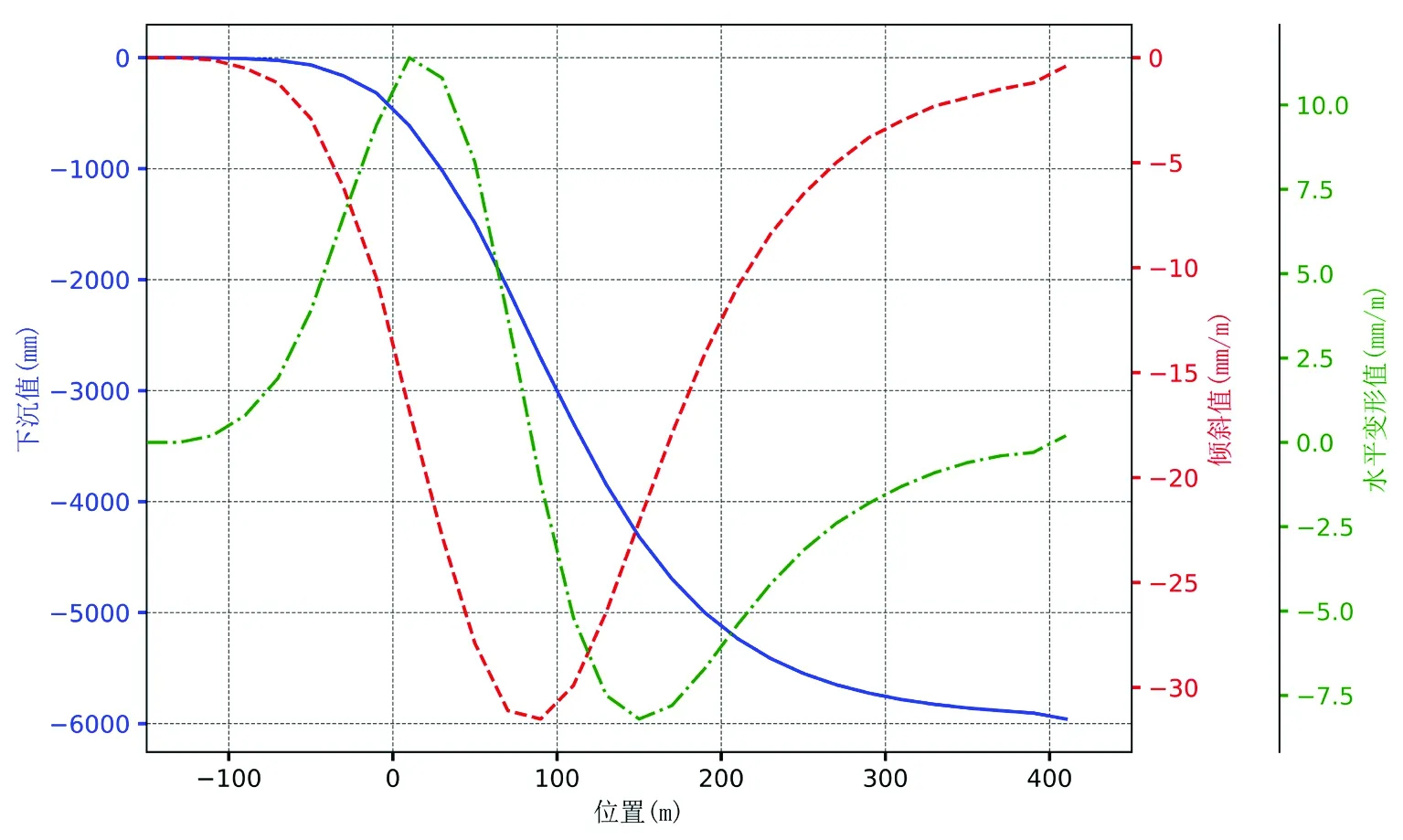
图7 河堤动态移动变形图

分别将概率积分法预测的、实测的河堤稳态、动态移动变形值及其他坡体稳定性预测参数输入坡体稳定性预测软件；将实测河提变形值计算的坡体稳定性评价系数作为真值，获得基于概率积分法的坡体稳定性评价系数误差散点图(图8)，预测值的平均误差、标准差和均方根误差如表3所示。总体来说，随着工作面的推进坡体稳定性预测误差逐渐增加，这是由于随着地表沉陷量的增大，概率积分法变形预测误差增加，进而导致坡体稳定性预测误差增大。当工作面推进至河堤前方390m时，坡体稳定性系数预测误差达到最大值-0.049，为实测稳定性评价系数的4.8%，说明使用概率积分法预测的坡体稳定性评价系数结果与实测值符合较好。另外，从预测结果可以看出，基于概率积分法的坡体稳定性预测结果普遍小于基于实测值的预测结果，这是由于为保证预测结果有一定的冗余性，概率积分法预测参数取值偏于保守造成的。

图8 基于概率积分法的坡体稳定性评价系数K预测误差散点图

平均误差标准差均方根误差-0.0100.0170.020

使用概率积分法预测的坡体稳定性评价系数K随工作面回采变化情况如图9所示，从图9可以看出，随着工作面的推进，河堤稳定性系数逐渐减小，其变化趋势与河堤顶端下沉变化趋势基本一致，这是由于随着下沉值的增大，计算系数增大，从而导致坡体抗滑力减小、下滑力增大；另外，相对于倾斜和水平变形来说，下沉值的数量级更大。当工作面推进至河堤前方约80m处时，河堤倾斜达到最大31.5mm/m，同时水平变形也相对较大，倾斜和水平变形的影响相对明显，从而造成河堤稳定性系数在此时发生较小的波动起伏，但河堤稳定性系数总体与河堤下沉变化基本保持一致的趋势没有发生改变。可以看出，采动坡体稳定性系数主要取决于采动引起的坡体下沉量的大小。

当工作面推进至河堤前方约160m处时，河堤顶端下沉值达到4.5m，河堤稳定性系数接近于1，随着下沉值的继续增大，河堤稳定性系数小于1并持续减小。预测结果表明，若不对河堤进行加固，极有可能发生滑坡。另外，当河堤处于开始拉伸阶段时，仍能保持一定时间的稳定。相对于在工作面开采之前对河提进行加固，在此阶段对河堤进行注浆加固，不仅可以减小钻孔作业的难度，同时由于拉伸会导致坡体节理张开，更有利于浆体向坡体弱节理面渗透，从而提高加固的质量。

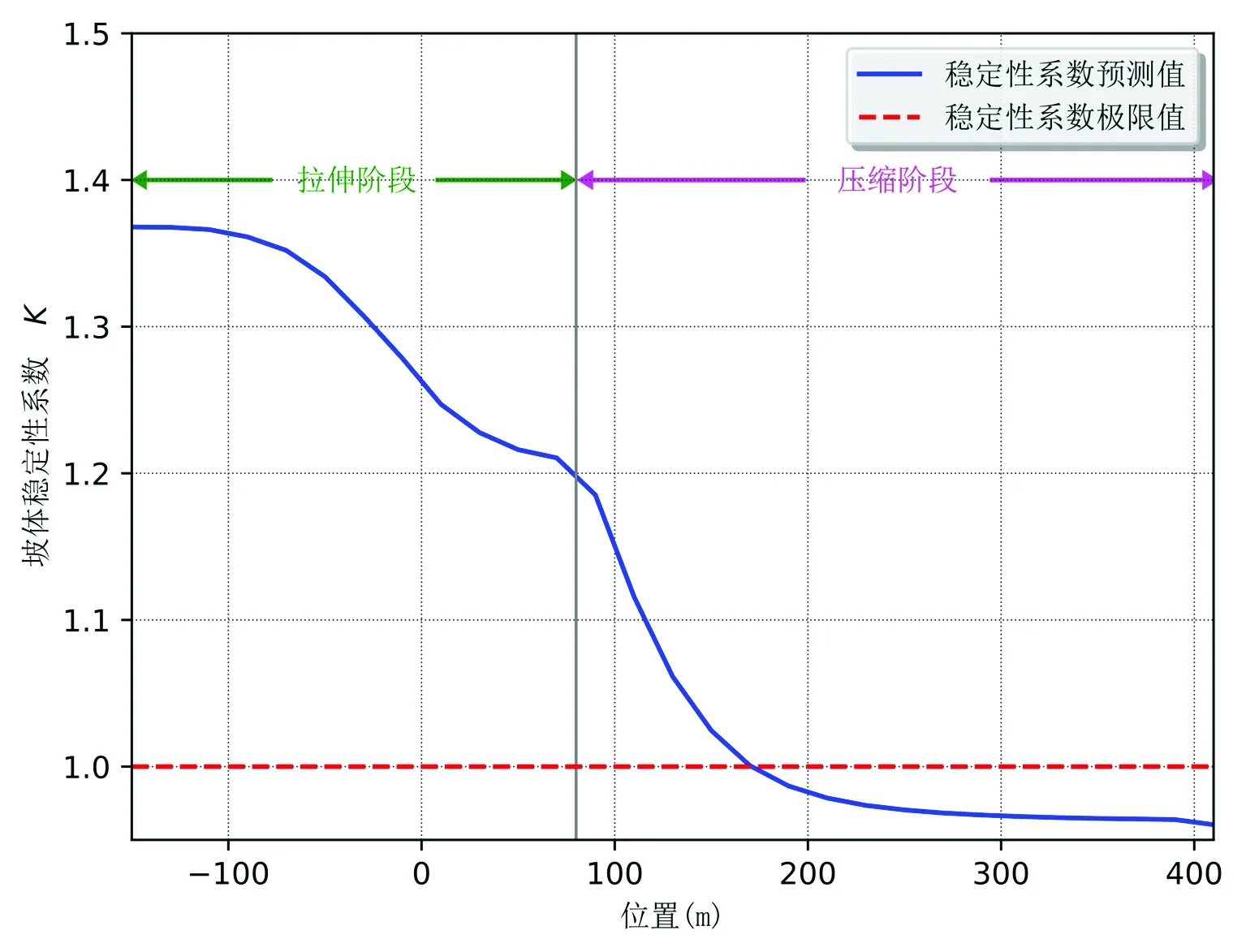
图9 采动引起的河堤稳定性动态变化图

5 结论

该文提出了使用概率积分法结合Knothe时间函数对采动坡体稳定性进行预测分析的方法，并使用C#语言编制了坡体稳定性预测程序，解决了采动坡体稳定性预测中人工计算繁琐、且容易出错的问题，能够满足采动坡体稳定性预测工作的需要，具有一定的实用推广价值。该文结合一个工程实例通过实测数据验证了提出方法的可行性；另外，通过对工程实例中的坡体稳定性预测和分析表明：

(1)采动引起的坡体下沉是影响坡体稳定性的主要因素；

(2)如果坡体在拉伸阶段仍能维持一定的稳定性，在该阶段进行注浆加固能获得更好的加固效果。

最后需要说明的是，坡体的移动变形值对坡体采动稳定性预测有较大影响，就文中提出的方法来说，移动变形预测值的准确性主要取决于概率积分法预测参数的准确性和可靠性。当项目区无相关的岩移观测资料时，应尽量参考类似采矿地质条件下通过岩移观测获得的概率积分法预测参数；并布设地表监测站，通过实测数据及时对预测参数进行调整，以提高预测精度。