施工升降机振动测试分析及应用研究

许 辉，刘丁丁，刘海华，田苗苗，朱 磊

（中联重科股份有限公司，湖南 长沙 410000）

1 测试平台的搭建

1.1 系统硬件的组成

施工升降机振动测试平台的系统硬件由各类NI采集模块（如9234、9237）、机箱（如9188）各类传感器（如加速度传感器）、数据存储设备和图形编程软件Labview组成，其系统框图如图1所示。

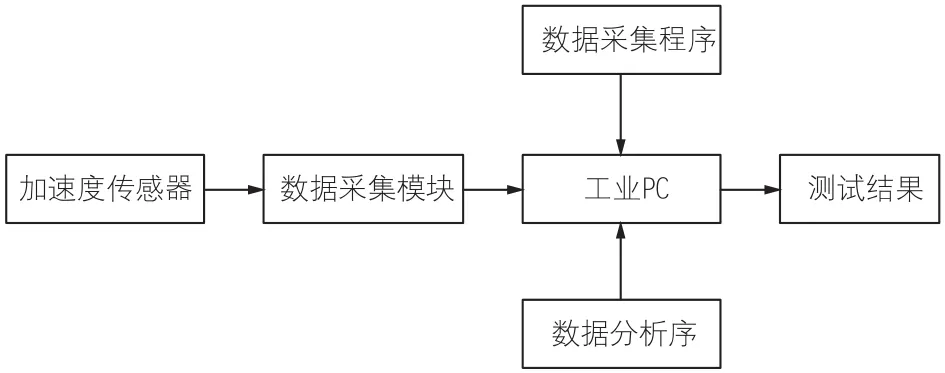
图1 施工升降机振动测试平台系统框图

1.2 数据分析的理论基础及程序编制

由于计算机及精密电子仪器、虚拟仪器的快速发展，特别是多通道、高分辨率的快速傅立叶变换（FFT）分析技术的应用，使得试验数据的频谱分析变得快速、准确和有效，所谓快速傅立叶变换（FFT）并不是一种新变换，而是离散傅立叶变换的一种新算法，对于一般周期函数x（t）可表达为

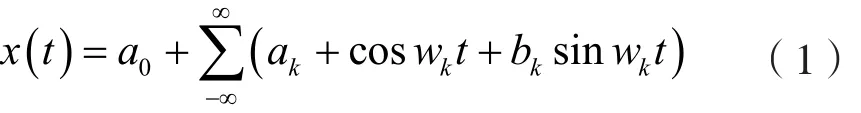
运用广义函数概念，可以认为X（t）的傅立叶变换由下式给出

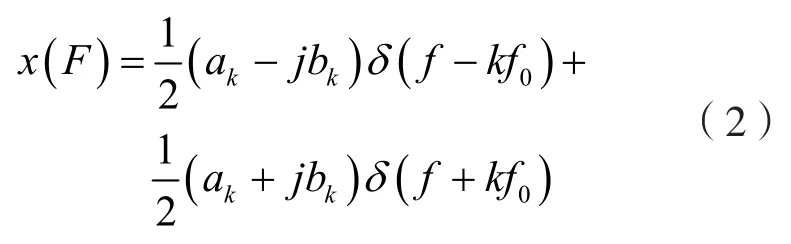
此处令

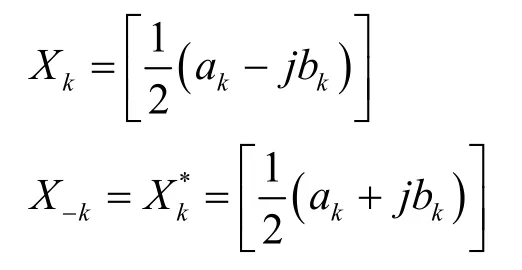
运用符号Xk，则其傅立叶变换对为

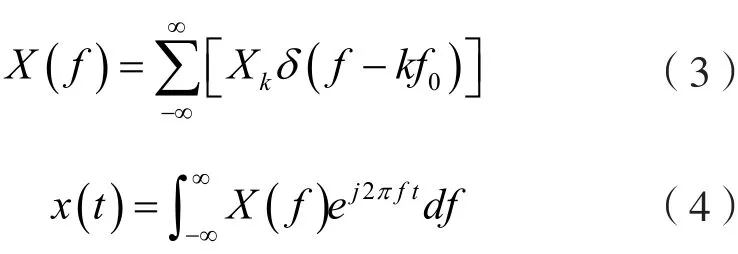
若将周期函数的1个周期T分为N等分，则式（3）中的Xk是离散序列Xr（r=0，1，2，…，N-1）的离散傅立叶变换，并可得以下离散变换对，即

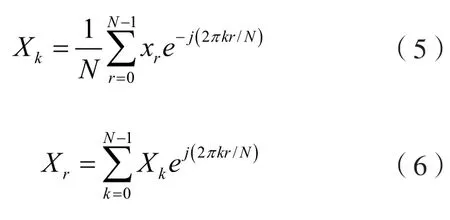
Labview是专为测量、数据分析并提交结果而设计的，其功能众多的图形用户界面又易于编程，广泛应用与仿真、结果显示、通用编程等方面，本文研究中的数据采集及数据频谱分析程序分别如图2和图3所示。

1.3 试验的具体方法

本文研究测试了施工升降机驱动系统及吊笼的振动加速度值，传感器安装布置情况如下：

（1）驱动系统左立柱上端，测量驱动架加速度值，如图4所示；

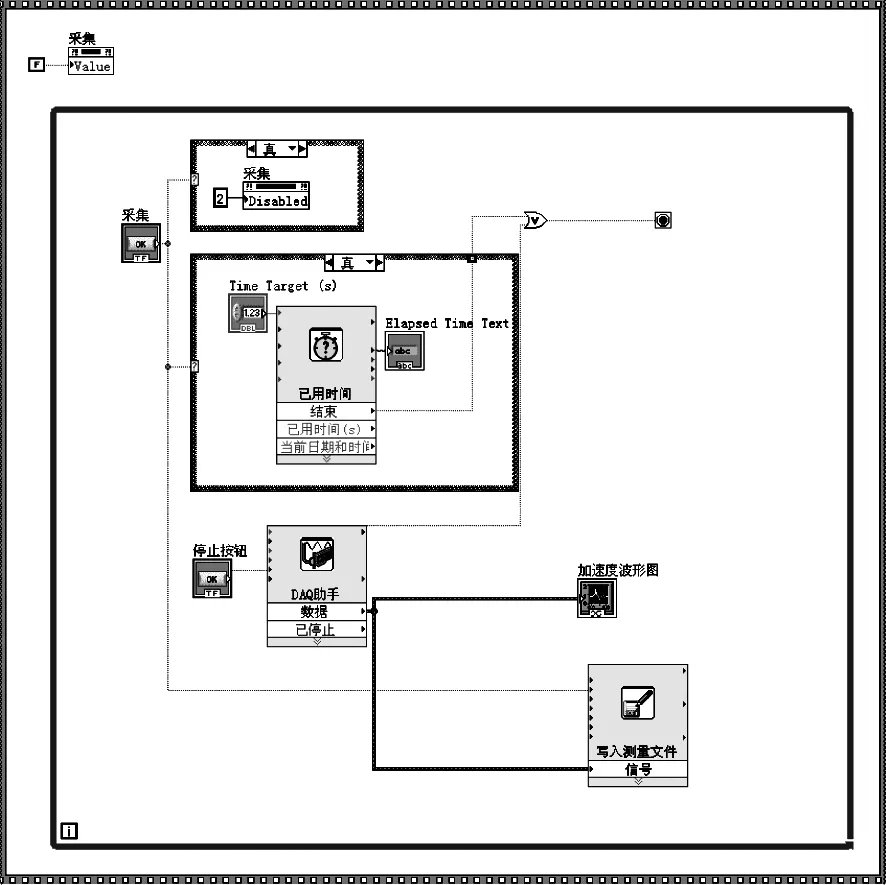
图2 数据采集程序

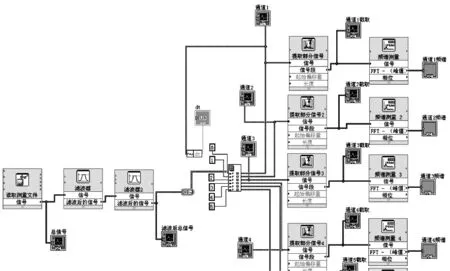
图3 数据频谱分析程序

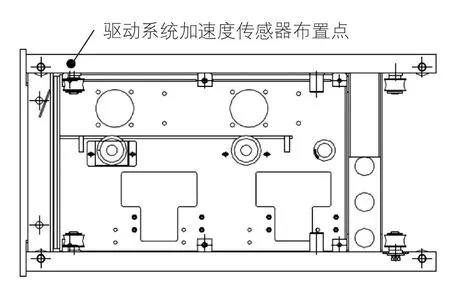
图4 驱动系统测点布置

（2）吊笼笼底左侧横梁，靠近司机室一端，测量笼底结构加速度值，如图5所示。

载荷放置按GB26557-2011中要求的单位面积载荷p＜4.0kN/m2，载荷均布于笼底板80%面积上，且处于最不利的位置，加额定载荷及1.25倍额定载荷，采用2个1t及1个0.5t的特制砝码，模拟2t或2.5t的试验载荷，载荷布置如图6中A1区域所示。

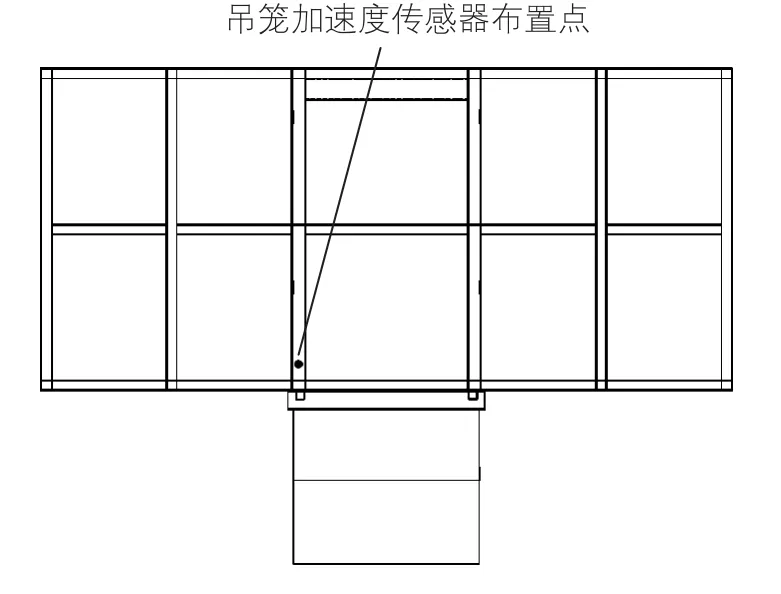
图5 吊笼测点布置

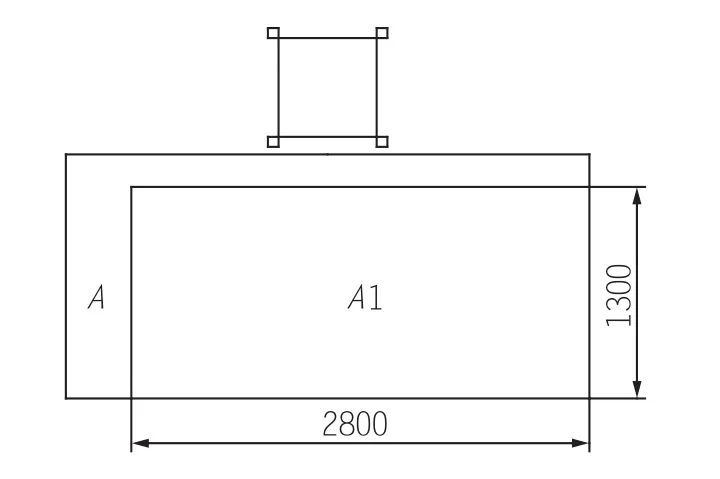
图6 载荷布置区域

按空载、额载两种状态，测量驱动架、吊笼测点处上行和下行的振动加速度，记录并存储数据。

2 振动测试分析

本文以SC200/200E二传动施工升降机为研究对象，按空载、满载及上行、下行工况进行试验，并记录和分析相关试验数据。

2.1 驱动架振动频谱分析

通过对测试数据进行频谱分析，经FFT后得到驱动架振动频谱图。

由图7可知，驱动架空载上行和下行时，振源的基频频率分别22.8Hz和23.6Hz，上行时振动能量主要集中在基频处，下行时振动能量主要集中在3阶倍频处，即70.8Hz。

由频谱分析可知振源基频为驱动系统齿轮与齿条的啮合频率，通过齿轮齿数（z=15）及减速机减速比（i=16）可计算出空载上行和下行时电机的转频分别为24.32Hz和25.17Hz，即电机转速为1459.2r/min和1510.2r/min，电机下行转速比上行快，处于发电状态。

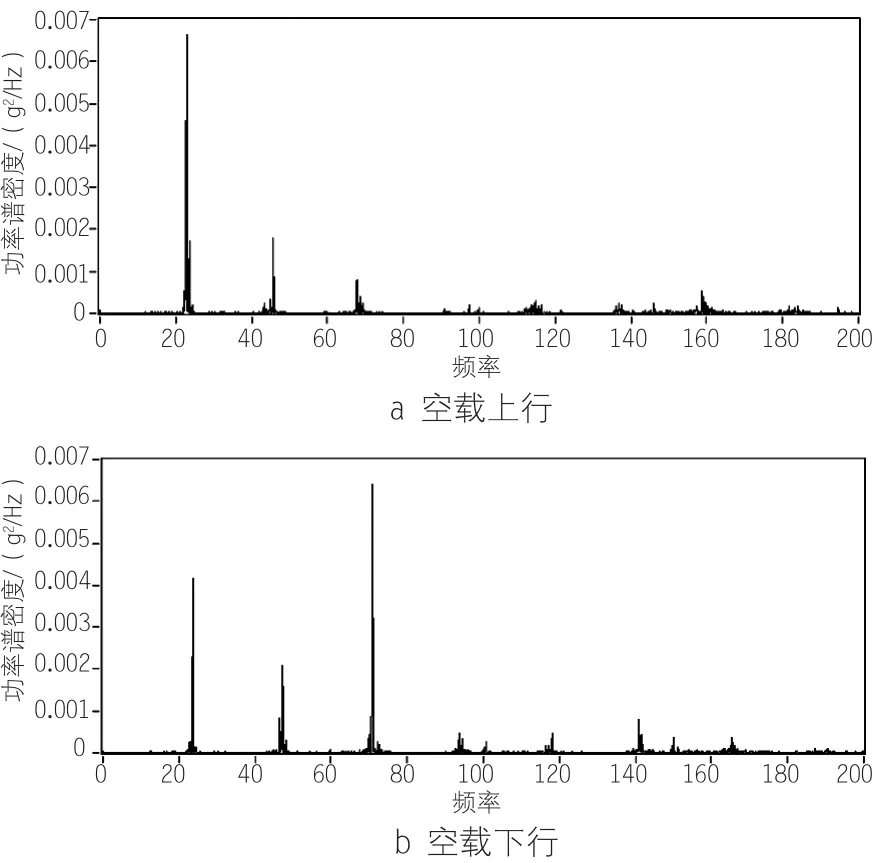
图7 驱动架空载振动频谱图

由图8可知，驱动架满载上行和下行时，振源的基频频率分别22.3Hz和23.8Hz，上行时振动能量主要集中在基频处，下行时振动能量主要集中在3阶倍频处，即71.4Hz。满载运行时，其振动频谱较空载运行时复杂，倍频成份更多，这是由于驱动架离振源更近，振动来不及衰减。上行和下行的频率差异特性与图7相似，即下行时电机运行更快处于发电状态，且满载上行比空载上行稍慢，满载下行比空载下行稍快。

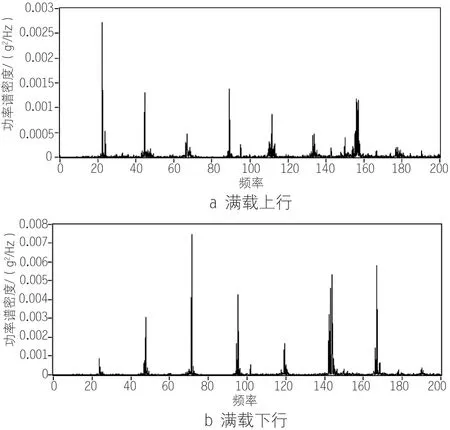
图8 驱动架满载振动频谱图

空载和满载时振动量值相差不大。

2.2 吊笼振动频谱分析

通过对测试数据进行频谱分析，经FFT后得到吊笼振动频谱图。

由图9可知，吊笼空载上行和下行时，振源的基频频率分别22.8Hz和23.6Hz，且上下和下行的振动能量都主要集中在基频处，振动频谱中倍频成分较少，这是由于吊笼距振源（驱动系统齿轮齿条啮合处）较远，其他频率成分振动能量衰减较快。上行和下行时的电机运行特性与前述分析一致。

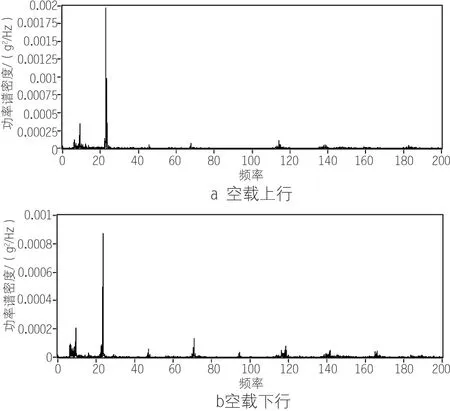
图9 吊笼空载振动频谱图

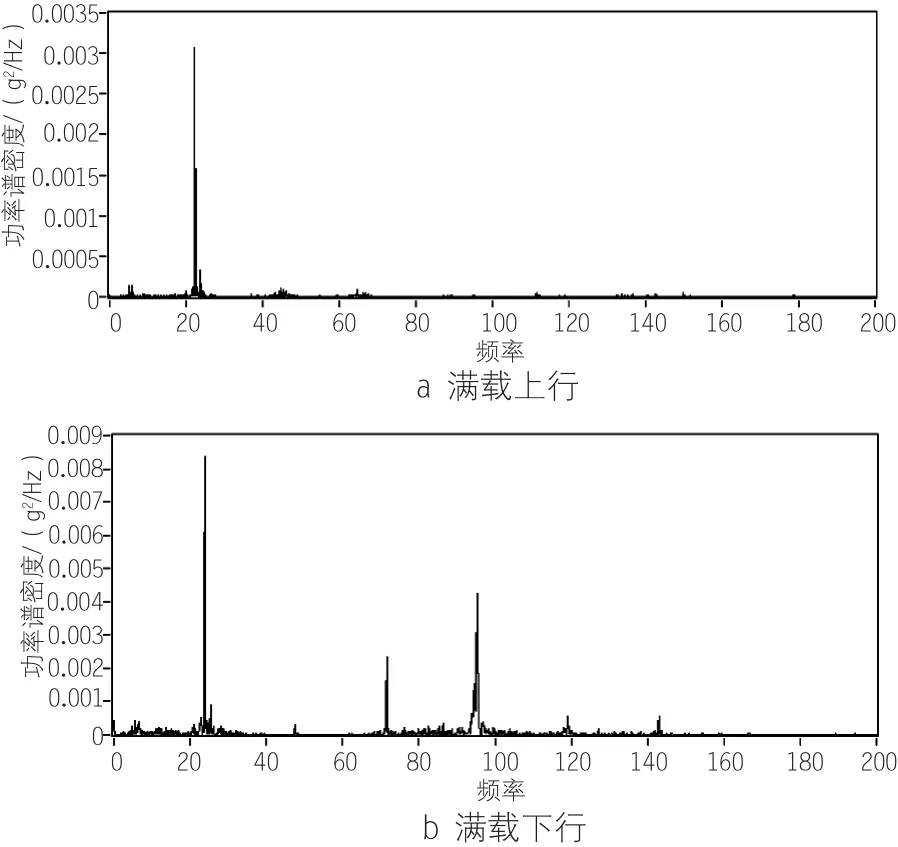
图10 吊笼满载振动频谱图

由图10可知，吊笼满载上行和下行时，振源的基频频率分别22.3Hz和23.8Hz，且上下和下行的振动能量都主要集中在基频处。上行和下行时的电机运行特性与前述分析一致。空载和满载时振动量值相差不大。

3 模态的有限元计算

3.1 驱动系统模态计算

以前述测试的驱动系统为例，该驱动系统由驱动架、驱动单元、背轮和滚轮等构成，由于计算需要，将滚轮、背轮等去除，电机和减速机外形简化，赋予相应的质量特性，在保证计算结果的前提下节省计算资源。运用通用的有限元计算软件Abaqus，导入驱动系统三维模型，并设置好材料特性及边界条件，计算得到系统固有模态，本文只计算前6阶固有模态。

由图11和表1可知，驱动系统前6阶固有模态与振源频率值22.3Hz、22.8Hz、23.6Hz、23.8Hz不重合，不会发生共振。

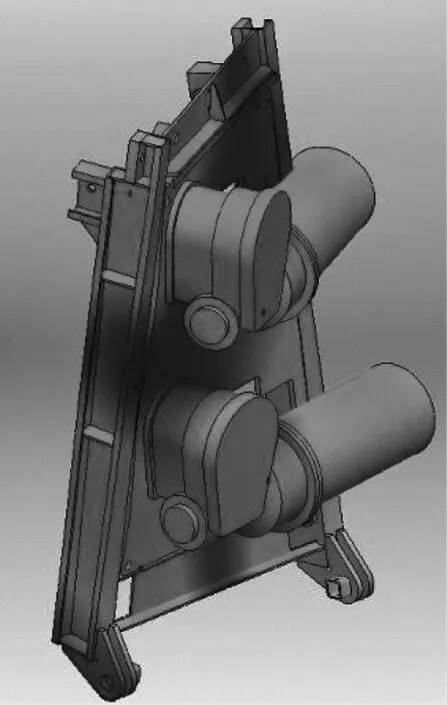
图11 驱动系统固有振型

3.2 吊笼模态计算

以前述测试的吊笼为例，该吊笼由笼架、网片、进料门、出料门、笼顶板、笼底板等组成，由于计算需要，保留笼架及笼底板，其余部件在原位置处赋予相应的质量特性，以保证计算结果的准确性，本文只计算前6阶固有模态。

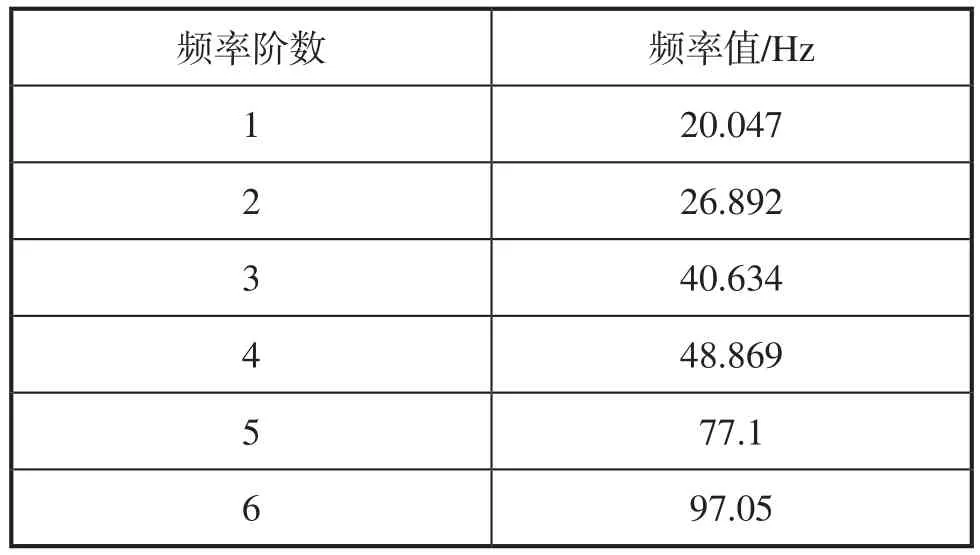
表1 驱动系统固有频率

由图12和表2可知，吊笼前6阶固有模态与振源频率值22.3Hz、22.8Hz、23.6Hz、23.8Hz不重合，不会发生共振。

图12 吊笼固有振型

4 结束语

（1）驱动系统、吊笼的振源基频频率为22.3～23.8Hz，由此可以推算出电机转频（即转速）和施工升降机实际运行速度；

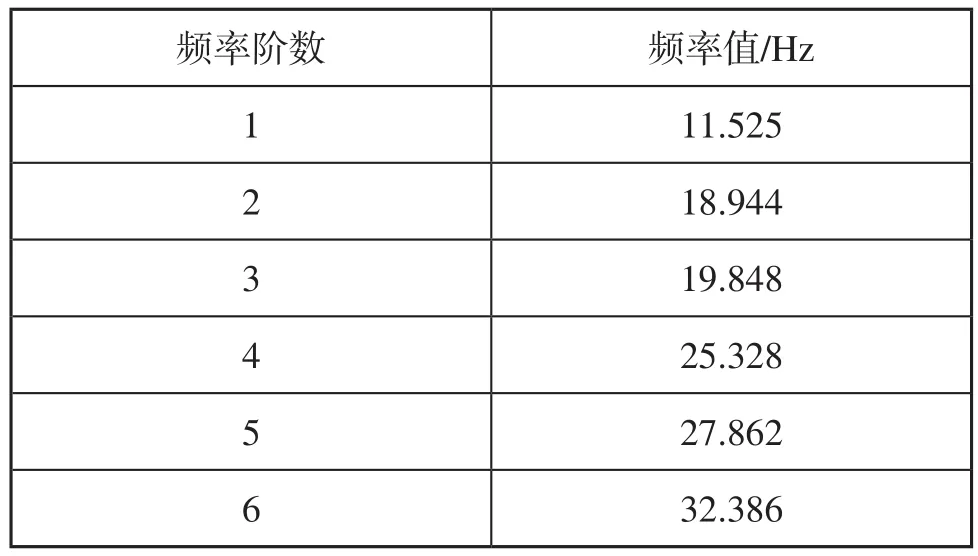
表2 吊笼固有频率计算值

（2）施工升降机下行时振源频率比上行时稍高，处于发电状态，电机转速＞同步转速1500r/min；

（3）空载上行的振源频率比满载上行的稍高，运行速度稍快，空载下行的振源频率比满载下行的稍低，运行速度稍慢；

（4）通过振动频谱分析及模态有限元计算值的对比，驱动系统及吊笼固有频率值与振源频率值不重合，不会发生共振，本文的研究对施工升降机各结构件的设计及优化具有一定的指导意义。