基于等效线性化的惯容减震结构优化设计

2018-11-22张瑞甫翁大根

结构工程师 2018年5期

罗浩张瑞甫翁大根沈华

(同济大学结构工程与防灾研究所,上海 200092)

0 引言

惯容器是一类具有两节点质量单元的新型控制装置,早期应用于车辆工程领域,近年来逐渐发展为建筑结构振动控制领域的研究热点之一[1]。根据惯性质量实现方式的差异,可将惯容器分为螺杆型、齿轮型和液压型三类[2]。调谐黏滞质量阻尼器(Tuned Viscous Mass Damper,TVMD)是一种基于位移增效原理的螺杆型惯容器。将这种阻尼器应用于结构时,结构的层间水平相对运动可转化为阻尼器内筒和质量的转动,使得阻尼器的黏滞阻尼效应和质量效应显著放大,从而可以降低结构的动力响应。

近十几年来,不少学者针对TVMD的研发与应用开展了研究工作。在1999年,Arakaki等[3]最早提出旋转阻尼管(Rational Damper Tube,RDT)的概念,它是通过轴承将纵向运动变为高速的旋转运动,以此放大纵向位移,达到增强阻尼的效果。2004年Saito等[4]对RDT进行了改进,通过在轴承上安装旋转飞轮,开发了有显著质量效应的黏滞质量阻尼器(Viscous Mass Damper,VMD)。2007年,Hwang等[5]将VMD与套索装置结合,证明该装置可以有效地降低结构的动力响应。2008年,Saito等[6]在VMD的基础上增加弹性,开发了具有调谐效果的黏滞质量阻尼器,即TVMD。2009年,Arai等[7]对设置黏滞阻尼器、VMD和TVMD的三种结构体系进行了比较分析,并将TVMD应用于弹塑性结构体系。2012年,Ikago等[8]基于定点理论给出了TVMD结构体系的参数优化设计公式,并对配置TVMD的结构体系进行了地震台试验,验证了TVMD对结构地震响应的控制效果。2013年,Lazar等[9]对附加TMD和TVMD的多质点体系进行了对比分析,结果表明采用TVMD可以获得更大的质量效应和更好的振动控制效果。2016年,Zhang等[10]分别将包括TVMD在内的四类阻尼器安装于结构底层,以位移峰值最小为目标,采用数值方法得到了四类不同阻尼体系的优化参数。

上述学者已对TVMD用于控制结构振动的有效性进行了证明,然而目前还没有可以考虑主体结构阻尼的TVMD参数设计方法。Ikago等[8]基于定点理论推导了TVMD参数设计公式,然而,该公式不能考虑主体结构阻尼的影响。对于实际结构而言,结构阻尼一般不宜忽略[11-16],设计过程中不考虑主体结构阻尼,可能使得设计参数与实际优化结果偏差较大。因此,本文采用了一种等效线性化方法,对现有基于定点理论推导的优化设计公式进行修正,从而得到考虑主体结构阻尼的TVMD参数优化设计公式。

1 TVMD结构体系响应分析

图1给出了附加TVMD的单自由度体系示意图。图中,m,kb和cb分别为主体结构的质量、刚度和阻尼系数;md,kd和cd分别为TVMD的等效质量、等效刚度和等效黏滞阻尼系数。

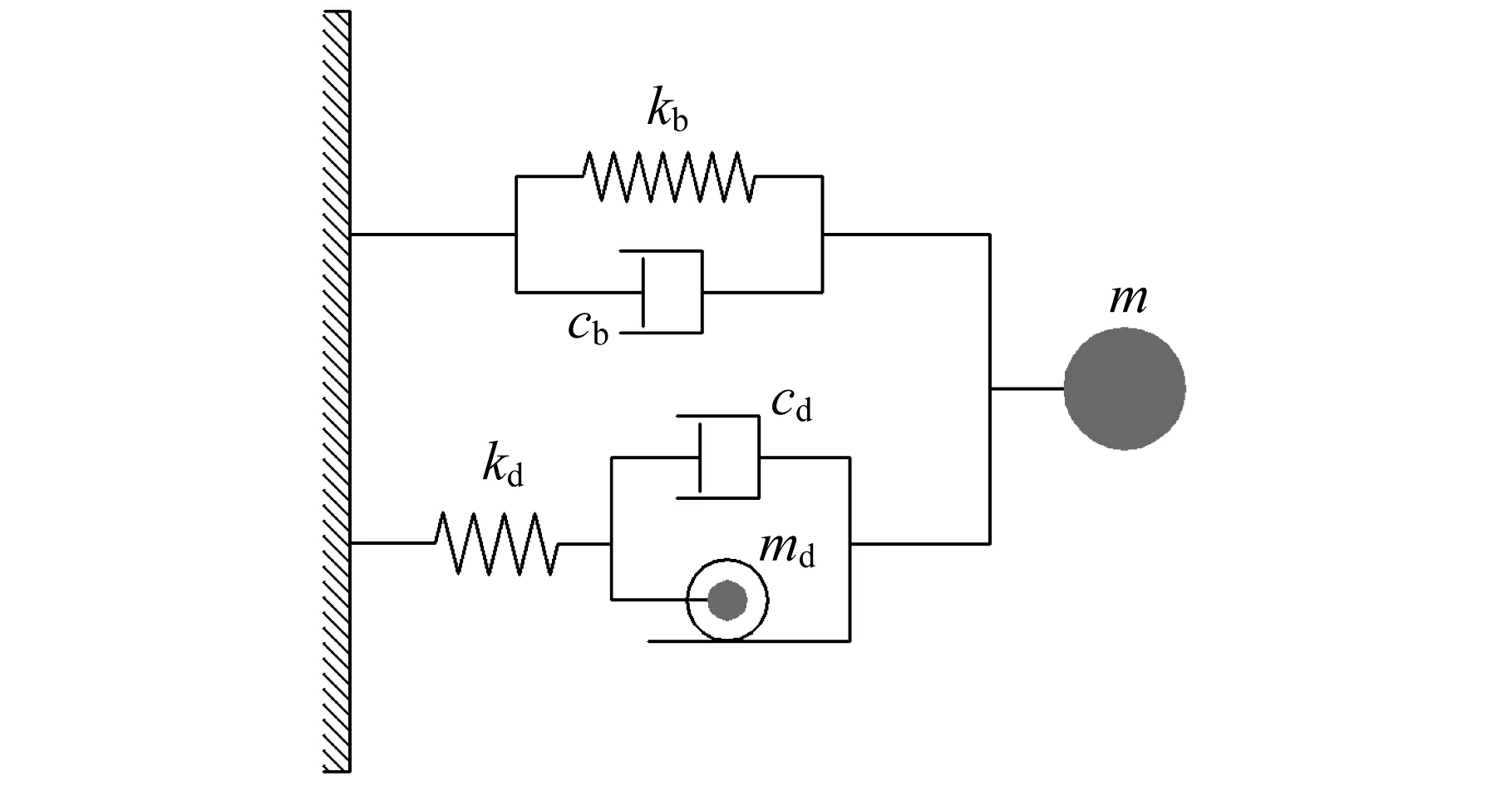
图1 附加TVMD的单自由度体系Fig.1 SDOF system with a TVMD

(1)

式中,x和xd分别为主体结构的相对位移和TVMD质量单元的相对位移。

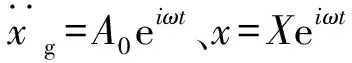
(2)

(3)

式中,

为对结构的位移响应进行优化控制,以位移放大系数的峰值最小为控制目标,对TVMD体系进行优化设计。从而得到优化问题:对于给定主体结构,取不同TVMD质量比μ,确定相应的频率比β和附加阻尼比ζ,使位移放大系数Rd的峰值最小。其数学模型可表示为

(4)

2 基于定点理论的TVMD结构优化设计

当不考虑主体结构阻尼时,令ξb=0,代入式(3),则可将配置TVMD的结构体系位移放大系数简化为

(5)

其中,

根据式(5),取结构固有圆频率为1.0 rad/s,质量比μ为0.1,频率比β为1.05,通过设置不同的TVMD附加阻尼比,可以得到位移放大系数Rd与激励频率比λ的一簇关系曲线,如图2所示。

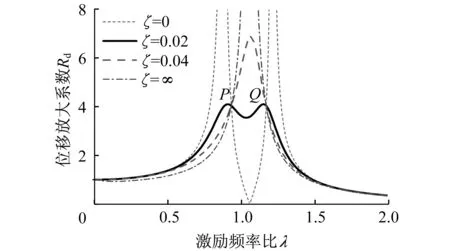
图2 TVMD体系频响曲线(ξb=0)Fig.2 Resonance curve of the TVMD system (ξb=0)

由图2可知,不同附加阻尼比时,各曲线相交于两个固定点P与Q。根据定点理论[17],要使位移放大系数的峰值最小,需满足:① P与Q点为曲线的峰值点;② P与Q点幅值相等。基于此理论,Ikago等[8]推导得到TVMD体系的优化频率比和优化附加阻尼比的表达式:

(6)

(7)

令刚度比κ=kd/kb,由式可得基于定点理论推导的TMVD体系优化刚度比为

(8)

根据定点理论推导的上述优化公式(下文记作Ikago公式)比较简单,便于计算使用。然而,这种方法的假设前提是主体结构不存在阻尼。实际上,当需要考虑主体结构阻尼时,定点理论的前提条件不再适用。比如,设结构固有圆频率为1.0 rad/s,结构阻尼比ξb为0.05,质量比μ为0.1,频率比β为1.05时,根据式(3),可以得到位移放大系数Rd与激励频率比λ的一簇关系曲线,如图3所示。

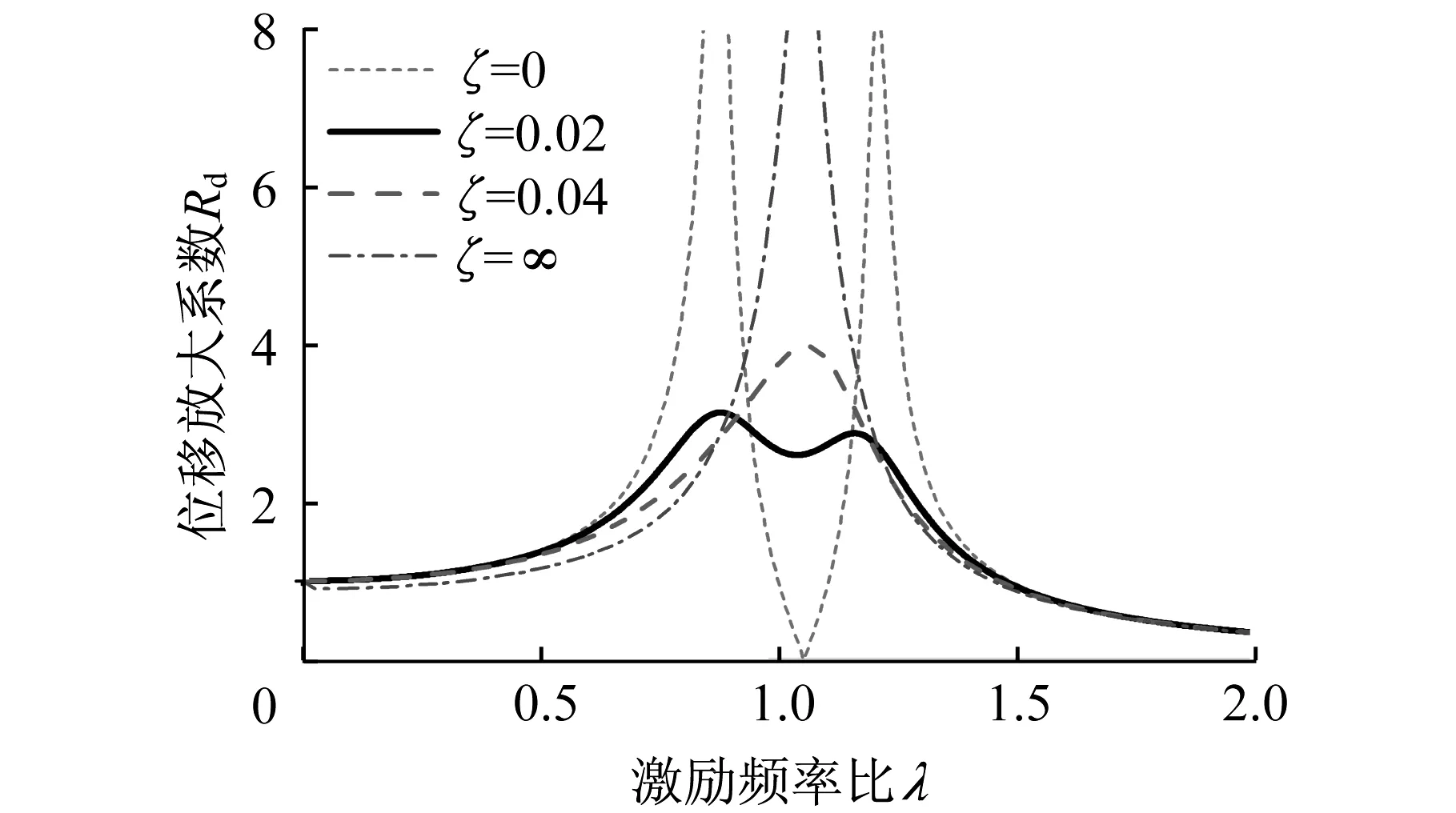
图3 TVMD体系频响曲线(ξb=0.05)Fig.3 Resonance curve of the TVMD system (ξb=0.05)

由图3可知,考虑主体结构固有阻尼时,不同附加阻尼比条件下的频响函数曲线并不存在固定点。因此,在这种情况下,定点理论的前提条件不再成立。在实际结构中一般均需考虑主体结构阻尼比的影响,比如钢筋混凝土结构常取阻尼比为0.05。对于一些阻尼较大的结构若采用这种方法设计,设计参数可能与优化结果相差较大。因此,有必要提出可以考虑主体结构阻尼的参数优化设计公式。

3 基于加权均方差最小的线性等效方法

考虑一个有阻尼的单自由度体系,其控制方程可写为

(9)

若将其等效为无阻尼体系,控制方程可改写为

(10)

式中:ωe为等效圆频率,令其满足下式:

(11)

(12)

最小。式中,参数γ与λ可由如下方程确定:

∂W/∂γ=0

(13)

∂W/∂λ=0

(14)

令x=acosφ,φ=ωet+φ0,Φ=ωeD,代入式(12)-式(14),可得参数γ与λ分别为

(15)

(16)

将式(15)代入(11),整理可得关于ωe的一元二次方程,求解该方程,并令Φ=π/2,可得:

(17)

常取ρ=1/2,式(17)可进一步简化为

(18)

因此,在给定结构阻尼和固有圆频率的情况下,可由式(18)确定其等效无阻尼体系的等效圆频率。

4 基于等效线性化方法的TVMD结构优化设计

对于TVMD结构的优化设计,为考虑主体结构阻尼对优化结果的影响,本文采用上述等效线性化方法,将有阻尼结构等效为无阻尼结构,再利用适用于无阻尼体系的Ikago公式,得到TVMD有阻尼体系的优化设计公式。将图1所示的TVMD有阻尼体系等效为TVMD无阻尼体系,如图4所示。图中,ke为等效体系的结构刚度。

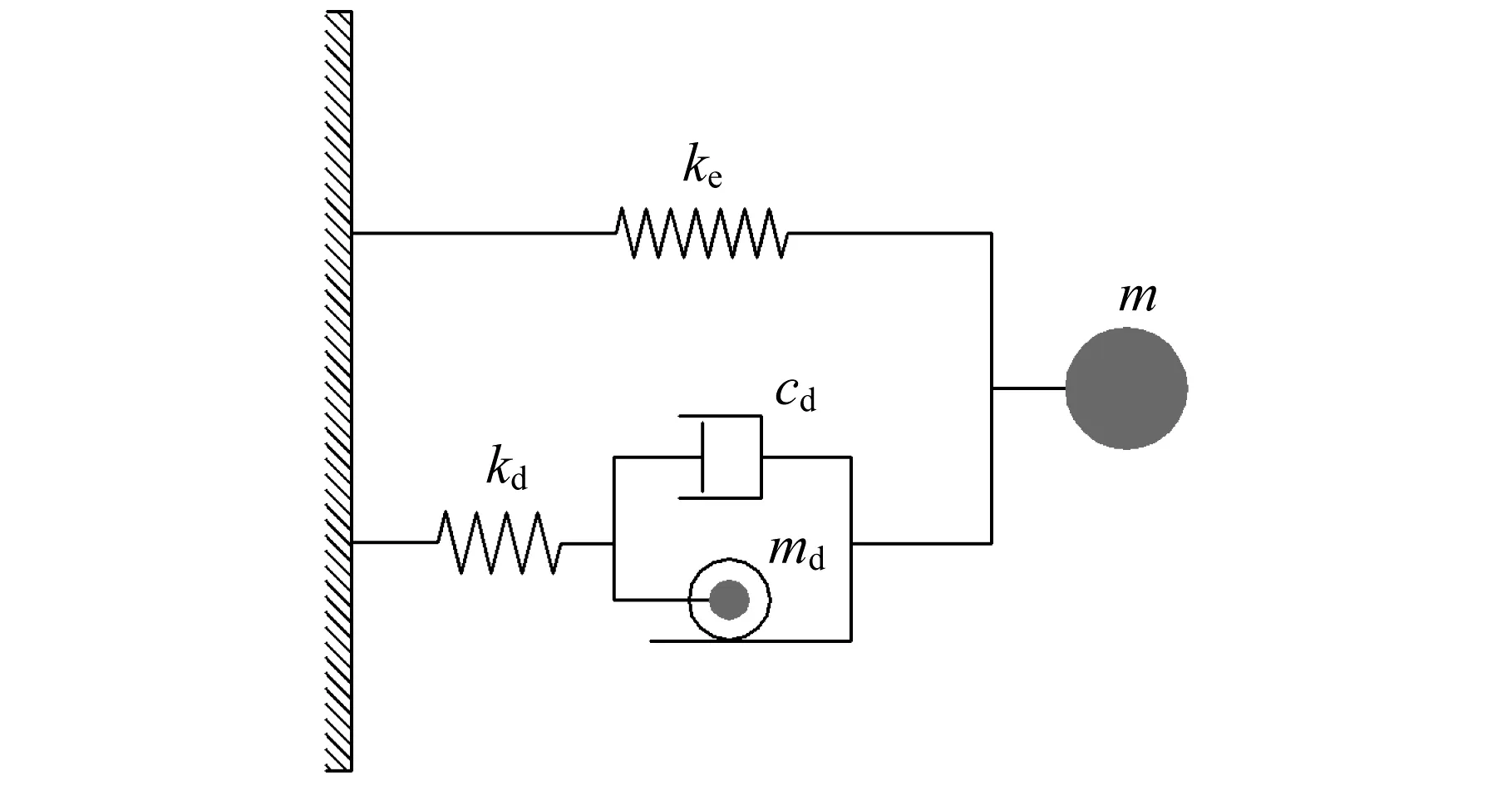
图4 TVMD等效无阻尼体系简化模型Fig.4 Simplified model of the equivalent un-damped system with a TVMD

(19)

针对图4所示的TVMD无阻尼体系,可根据定点理论得到相应的优化设计公式。因此,根据式(6)-式(8),可得TVMD有阻尼体系的优化频率比、附加阻尼比和优化刚度比分别为

(20)

(21)

(22)

由式(20)-式(22)可知,TVMD有阻尼体系的优化参数可通过在定点理论所得优化结果的基础上乘以修正系数η或者η2而得到。将ξb=0代入式(19),可得修正系数η的值为1,因此,式(20)-式(22)也适用于TVMD无阻尼体系。

5 比较分析

为验证本文提出的TVMD体系参数优化公式的合理性,对无TVMD的结构体系(ST0)、采用Ikago公式设计的TVMD体系(ST1)和采用本文修正公式设计的TVMD体系(ST2)三种体系进行比较分析,图5分别给出了三种体系的位移放大系数与激励频率比的关系曲线,相应地,表1分别给出了不同结构阻尼比情况下,两种优化方法设计的优化刚度比、附加阻尼比和TVMD体系位移放大系数峰值。

由图5可知,对于无阻尼结构体系,两种优化方法得到的频响曲线完全重合,均有两个幅值相等的峰值点。然而,对于有阻尼体系,基于定点理论设计的TVMD体系的频响曲线有两个数值相差较大的峰值点,而采用本文修正公式设计的TVMD体系的频响函数两个峰值相差较小,相应的位移放大系数最大值更小。

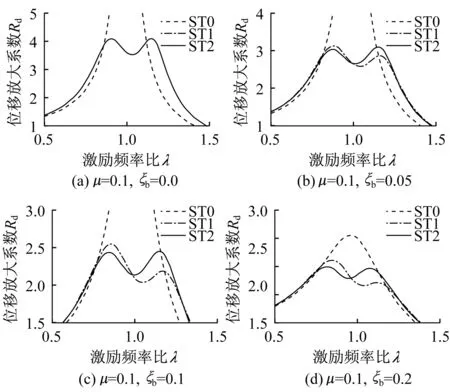
图5 两种优化方法TVMD体系的频响曲线Fig.5 Resonance curves of different TVMD systems

由表1可知,对于设置TVMD的有阻尼结构体系,随着结构阻尼比增大,按本文修正公式计算的优化频率比和优化附加阻尼比随之减小。然而,由于Ikago优化公式没有考虑主体结构阻尼影响,若采用该公式进行优化设计,则不论结构阻尼比多大,所得优化频率比与优化附加阻尼比均与ξb=0的情况一致。针对有阻尼结构体系,与Ikago公式所得结果相比,本文修正公式所得优化刚度比和优化附加阻尼比更小,从而可以使得设计更加经济。同时,与按照Ikago公式设计的体系响应相比,按照本文修正公式设计的TVMD体系的位移响应峰值更小,位移响应的控制效果更好。由表2可知,随着质量比的增大,按两种方法计算的优化频率比和优化附加阻尼比均随之增大;但由于修正系数不变,两种方法计算的参数之比不变。随着质量比的增大,两种体系的位移响应峰值均随之降低;与按照Ikago公式设计的体系响应相比,按照本文修正公式设计的TVMD体系的位移响应峰值更小,位移响应的控制效果更好。

表1两种优化方法的设计结果比较(μ=0.1)