富水地层双线小净距土压平衡盾构开挖面稳定性研究

2018-11-22戴志成吴文彪陈怀伟

铁道标准设计 2018年12期

王闯,封坤,戴志成,吴文彪,林辉,陈怀伟

(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031； 2.粤水电轨道交通建设有限公司,广州 510610；3.浙江省机电设计研究院有限公司,杭州 310051)

随着我国经济社会的发展，城际铁路逐渐成为大型城市群间相互连接的重要交通方式，而盾构法因其施工速度快、风险低、对城市地面交通影响小等优点而成为城际铁路隧道穿越复杂环境工程的首选。然而，盾构掘进施工过程中不可避免会对周围地层产生扰动，尤其当地下水位较高时，由于渗透力的作用易导致开挖面失稳，对周围环境造成严重危害，应引起高度重视[1]。

针对渗流条件下的盾构隧道开挖面稳定性，众多学者开展了一系列研究。Anagnostou 等[2]根据滑动块为矩形楔形体时的极限平衡条件，研究了地下水条件下盾构开挖面的极限支护压力。高健[3]推导了考虑地下水渗流时盾构穿越高地下水位地层隧道掘进面支护压力解析表达式。乔金丽等[4]利用太沙基有效松动土压力理论和上限定理，推导了渗流作用下盾构穿越多层土的隧道开挖面极限支护压力的计算公式。LIU Wei 等[5]在建立成层土中地下水渗流模型的基础上，推导了考虑地下水渗流的盾构开挖面极限支护压力上限解。宋曙光[6]基于构建的三维旋转体优化破坏模型，推导了开挖面渗流力和坍塌土体中的渗流力求解公式，得到了渗流作用下复合地层中开挖面支护压力上限解。梁禹等[7]运用极限平衡法，在考虑隧道纵坡坡度及超孔隙水压力影响条件下，对隧道极限支护力计算公式进行了修正。黄阜等[8]基于极限分析上限定理和空间离散技术，构建了适用于在饱和土体中掘进的盾构隧道开挖面上限破坏机制。Buhan等[9]考虑地下水的作用，建立了土压平衡盾构开挖的数值模型，发现渗透作用对开挖面稳定性影响较大。康志军等[10]对考虑完全流固耦合效应的盾构隧道开挖面失稳过程进行了模拟和验证。

现有考虑渗流作用的盾构隧道开挖面稳定性分析中，主要针对单线隧道开挖面的极限稳定状态开展，而考虑双线隧道近接施工扰动时开挖面稳定性的影响未见报道。鉴于此，本文提出了基于屈服接近度的隧道开挖扰动分析方法，并结合广佛环线沙堤隧道工程，建立FLAC3D流固耦合分析模型，并考虑了地下水渗流作用影响，分析了富水地层双线小净距土压平衡盾构隧道在不同纵向开挖间距下先行隧道开挖面扰动行为，评价了富水地层双线盾构施工时开挖面的稳定性，该方法可为类似工程设计和施工提供参考。

1 渗流作用下开挖面稳定性分析

1.1 基于屈服接近度的开挖面扰动分析

隧道开挖扰动引起围岩性质的弱化，根本是其力学性质的弱化，因此岩体应力状态的变化能够反映隧道开挖的扰动程度。而岩土体内一点的应力状态，可以由主应力构成的主应力空间来描述；如图1为π平面上一点A的应力状态，当主应力空间中应力点满足相应极限平衡条件时，则构成了屈服面。

图1 π平面上一点应力状态示意

根据主应力空间内初始屈服面与未屈服应力点的相互关系，周辉等[11]提出了屈服接近度(YAI)的概念，即空间应力状态下的一点沿最不利应力路径到屈服面的距离，与相应的最稳定参考点在相同罗德角方向上沿最不利应力路径到屈服面的距离之比，并推导了基于Mohr-Coulomb准则的屈服接近度计算函数(式(1))。当应力点在屈服面上时，屈服接近度YAI的值为0，在等倾线上时为1，即YAI∈[0,1]。

YAI=

(1)

式中，I1为应力张量的第一不变量；J2为偏应力张量的第二不变量；θσ为应力罗德角；c为地层黏聚力；φ为摩擦角。

基于上述屈服接近度的概念，将隧道开挖面岩体主应力值及相关参数代入式(1)，可得隧道开挖前后开挖面的屈服接近度分别为YAI0和YAI1；通过比较YAI0和YAI1数值的差异性，即可判断隧道开挖对岩体的扰动程度及其稳定性。

1.2 流固耦合计算理论基础

基于屈服接近度的概念，从主应力状态变化程度对隧道开挖岩体稳定性进行评价；而对于地下水因素的考虑，结合FLAC3D有限差分软件提供的流固耦合计算模块来实现。首先利用FLAC3D软件建立数值分析模型并进行隧道开挖的流固耦合计算，然后利用屈服接近度概念对开挖岩体稳定性进行分析，从而实现对流固耦合作用下隧道开挖稳定性的评价分析。

流体在介质中流动时，主要引起孔隙水压、饱和状态、渗透流量的改变。在利用FLAC3D有限差分软件进行流固耦合计算时，地层中孔隙水压、饱和状态、体积应变等应力场及渗流场量值的变化关系满足相应的流动方程、平衡方程和本构方程[12]。由于地层水文地质参数有限，进行盾构隧道开挖的流固耦合计算时，结合FLAC3D软件的计算原理，将岩体视作多孔介质，假设地层水平渗透系数与竖向渗透系数一致，采用各向同性渗流模型进行计算，流体在岩土体内的运动满足Darcy渗流定律

qi=-k[p-ρfxjgi]

(2)

式中，k为介质的渗流率；ρf为流体的密度；gj(j=1,2,3)为重力加速度的3个分量。

流固耦合计算时渗流场和应力场的关系符合Biot固结理论，且本文中只涉及饱和土体的渗流，相应的控制方程如下

Δσij+αΔpδij=Hij(σij,Δξij)

(3)

式中，Δσij为应力增量率；α为Biot系数；Δp为孔隙水压力增量；δij为Kronecher因子；Hij为给定函数；Δξij为总应变增量。

2 数值模型建立

2.1 工程概况

广佛环线沙堤隧道位于佛山市南海区和禅城区内，设计起点里程DK1+615 m，终点里程DK7+830 m，为双线隧道；隧道全长5 985.731 m，盾构段全长5 035 m。其中隧道自3号井始发时双线最小间距仅3 m，最小覆土厚度6.5 m，始发后长距离穿越南北大涌河，为典型的小净距双线水下盾构隧道。图2为广佛环线沙堤隧道3号井始发段的线路平面情况，由于存在较大的施工风险，施工时对3号井始发段纵向加固28 m(17.5环距离)，并在始发区一定范围内对南北大涌河进行了临时改道。

图2 3号井始发区段线路平面示意(单位：环)

3号井始发段隧道范围内地下水类型为第四系孔隙水，补给主要通过大气降水入渗及南北大涌侧渗。含水层主要为第四系海陆交互沉积层中的粉砂、细砂、中砂、粗砂及强、弱风化砂岩；含水层分布广泛连续，富水较好～好，透水中等～强。强、弱风化砂岩厚度较大，分布广泛，岩体裂隙较发育或稍发育，含有较为丰富的地下水，富水性较好，透水性一般。图3为隧道施工时外送的渣土，由于隧道范围内地下水丰富，开挖引起地下水向隧道内渗流，土仓渣土呈流塑状。

图3 土仓流塑状渣土

该区间隧道设计管片内径7.7 m，外径8.5 m，幅宽1.6 m，厚度0.4 m，采用错缝拼装方式，管片衬砌混凝土强度等级为C50。工程中采用2台土压平衡盾构机进行作业，并考虑始发段小净距及富水地层等复杂因素所带来的风险，先进行左线始发掘进，在保持一定纵向施工间距的情况下进行右线的始发掘进。因此，针对该工程3号井始发段的特殊工程特点，研究双线隧道不同纵向开挖间距下的施工“叠加效应”。考虑始发段有一定的加固范围，以未加固段的典型断面位置处地层条件(图4)为依据，进行数值模拟分析。其中虽然南北大涌河改道但地下水丰富，设水位线位于地表处；双线隧道在该断面处埋深11.5 m，净距6.10 m。

图4 计算断面地层地质示意(单位：m)

2.2 数值模型

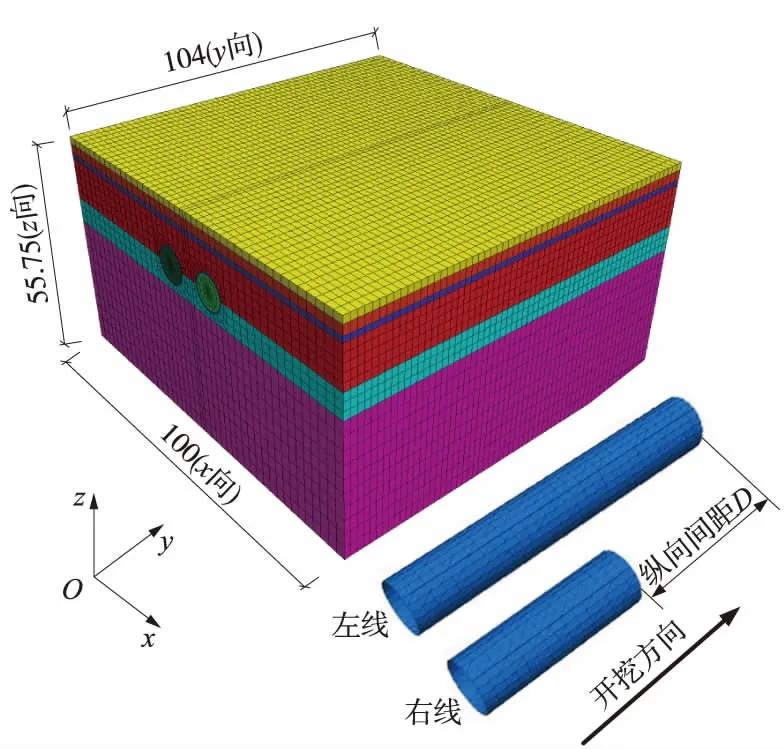
图5 三维数值模型(单位：m)

利用FLAC3D软件建立考虑双线隧道纵向施工间距的流固耦合数值计算模型，如图5所示。根据实际工程左右线的纵向间距，考虑力学和渗流边界效应，模型总体尺寸为100 m(X轴)×104 m(Y轴)×55.73 m(Z轴)。力学边界中地表为自由面，四周及底面采用法向位移约束条件；渗流边界条件中地表为透水边界(水头为0)，模型底面为弱风化岩层，设定为不透水边界；该区段地下水丰富，模型四周设为水头边界，隧道开挖掌子面设为透水边界。

模型中岩土体为理想弹塑性模型，遵循Mohr-Coulomb屈服准则；管片为C50钢筋混凝土材料，采用Shell结构单元模拟；考虑盾构注浆层的作用，并根据张云等[13]的研究，将盾尾间隙概化为均质、等厚、弹性的等代层，且根据工程中盾尾间隙的实际大小将等代层的厚度取为0.3 m。地层及材料的力学和渗流参数取值如表1所示。

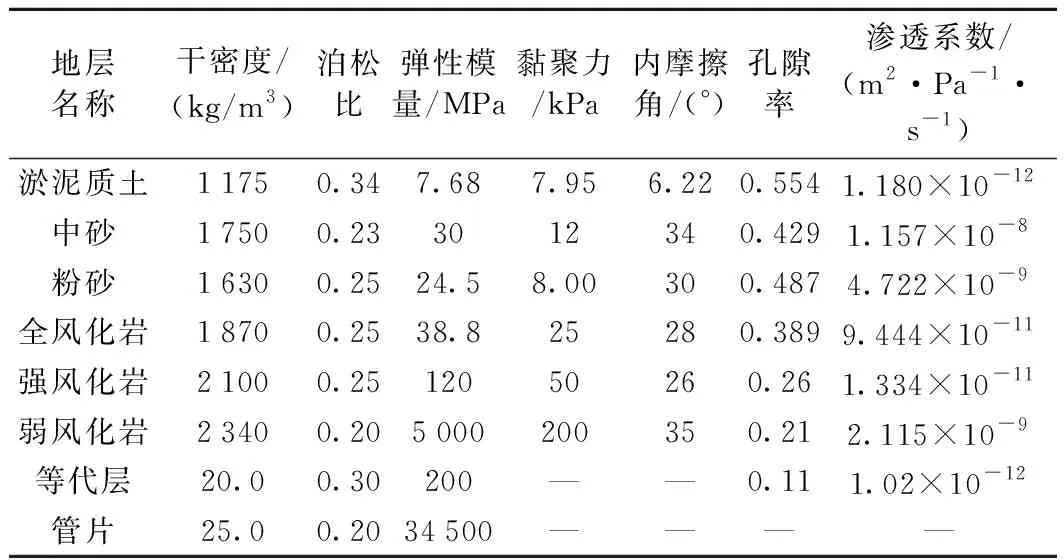
表1 各土层及材料主要物理参数

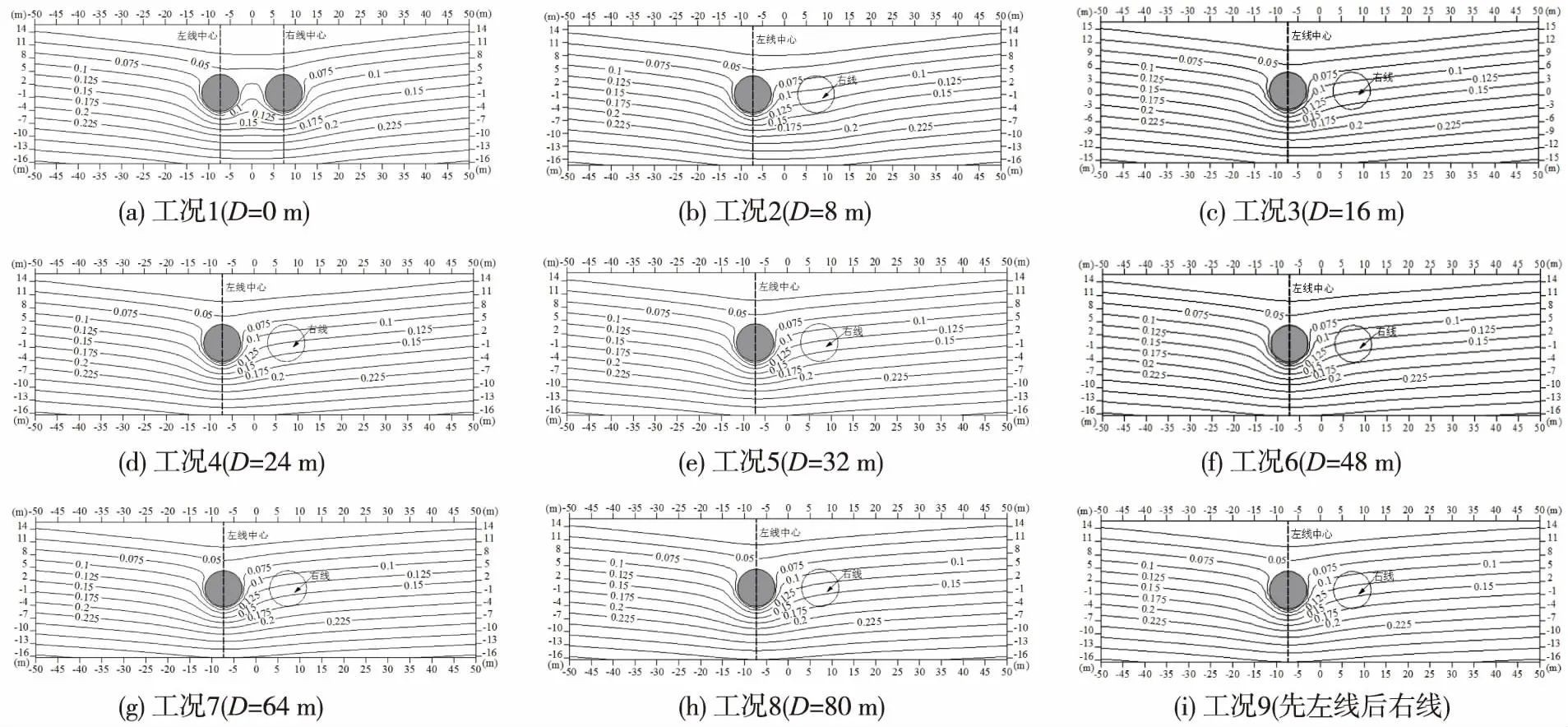
图7 监测断面处先行隧道开挖面水压力分布(单位：MPa)

图6为土压平衡盾构隧道开挖计算模拟示意，通过在开挖面上施加梯形荷载，以模拟土仓压力，改变单元性质，实现对注浆层和管片衬砌的模拟。考虑FLAC3D流固耦合计算的效率，设置单线施工模拟的循环进尺为8 m(5环管片的拼装施工)；根据文献[14-15]中的盾构开挖流固耦合数值模拟流程，每个开挖步内先进行力学计算，后进行流固耦合计算至设定时间。计算中左线先始发，并通过设置左线和右线模拟开挖的先后距离，改变其纵向开挖间距D。

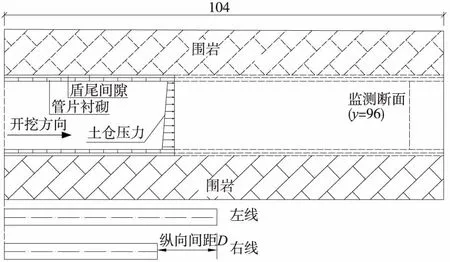
图6 施工模拟计算示意(单位：m)

针对双线盾构隧道纵向开挖间距D的差异，设置了9种计算工况，分别为D=0 m(左右线同时开挖)、D=8 m(5环)、D=16 m(10环)、D=24 m(15环)、D=32 m(20环)、D=48 m(30环)、D=64 m(40环)、D=80 m(50环)、D=104 m(先左线后右线)，沿纵向在y=96 m位置处设置监测断面，根据不同工况下左线隧道开挖至该监测断面时的状态量，分析先行隧道开挖面的稳定性。

3 数值计算结果分析

3.1 开挖面渗流场分析

现以设定的监测断面为目标面，得到不同工况下左线隧道开挖至监测断面时开挖面的渗流场分布，如图7所示。

由图7可知，土压平衡盾构隧道施工时，在开挖面的位置处形成明显的“渗流漏斗”，水压力呈向隧道内凹陷的漏斗状对称分布，地下水向隧道内部发生渗流，且在开挖面上水压力的漏斗状分布在距隧道中心一定距离后逐渐收敛。当左线和右线同时开挖时，在双线隧道开挖面附近水压力均呈漏斗状分布；当左线先于右线开挖时，岩体水压力的漏斗状分布主要存在于左线隧道附近。随着纵向开挖间距的增大，先行隧道开挖面的水压力分布，趋向于以左线隧道中心为轴线呈近似对称分布；各工况中当左、右线纵向开挖间距大于32 m时，先行隧道开挖面处水压力分布基本相同，说明纵向渗流场的影响范围为4～5倍洞径，在此范围外后行隧道施工对先行隧道开挖面的渗流场扰动很小。

当地下水流入隧道开挖面时，在开挖面附近由于水头差的作用，会形成作用在土体骨架上的渗透力。而盾构隧道开挖面的稳定性，取决于作用在土体骨架上的有效支护压力和水头差作用引起的作用在开挖面的渗透力，且渗透力在总支护压力中占有重要比重[3]。如图7所示，当左、右线同时开挖时，先行隧道开挖面附近地下水渗流最明显，此时作用在开挖面岩体骨架上的渗透力也最大，开挖面的稳定性最低；随着纵向开挖间距的增大，双线隧道开挖对先行隧道开挖面渗流场的影响差异性逐渐减弱，后行隧道开挖而引起的先行隧道开挖面岩体上的渗透力减小；即说明当纵向开挖间距较大时，就渗流场扰动方面而言后行隧道开挖对先行隧道开挖面稳定性影响很小。

3.2 开挖面扰动分析

设先左线后右线开挖(D=104 m)工况下先行隧道开挖至监测断面时开挖面的最小屈服接近度为YAI0，并通过式(4)定义后行隧道施工对先行隧道开挖面最小屈服接近度的扰动率n

(4)

式中，YAI为不同纵向间距下先行隧道开挖至监测断面时开挖面的最小屈服接近度。

利用式(1)和式(4)得到各工况下先行隧道开挖面的最小屈服接近度及其扰动率如表2所示，各工况下先行隧道开挖面最小屈服接近度变化趋势如图8所示。

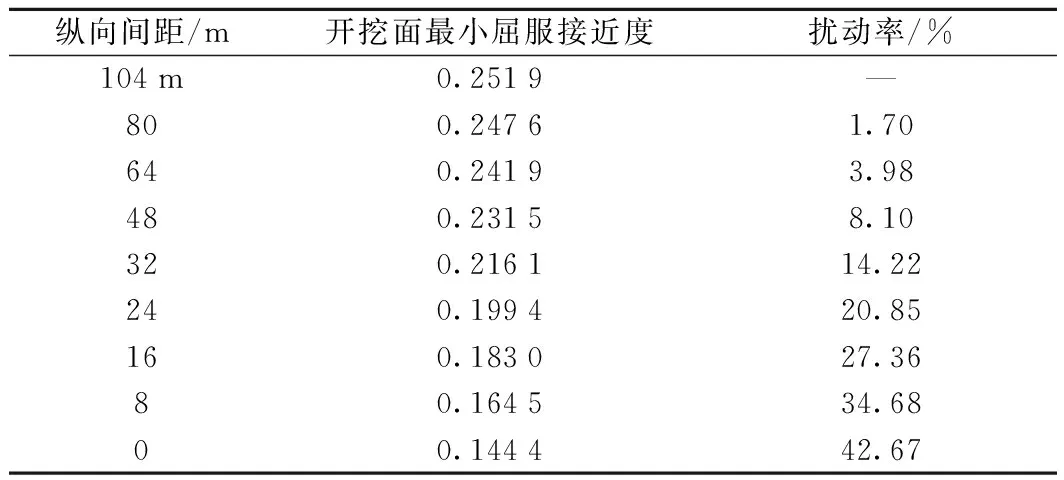
表2 不同纵向间距下开挖面最小屈服接近度

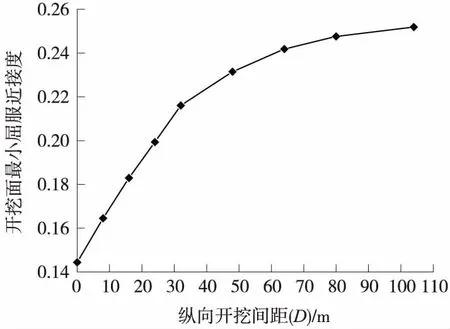
图8 监测断面处开挖面最小屈服接近度变化曲线

由图8可知，随着双线隧道纵向间距的增大，开挖面最小屈服接近度逐渐变大，隧道开挖引起的地层扰动程度逐渐减小，且这种变化趋于平缓。根据表2，以纵向间距为104 m(先左后右)工况下开挖面最小屈服接近度为参考，当纵向间距大于48 m时，后行隧道开挖对先行隧道开挖面最小屈服接近度的扰动小于10%，即先后行隧道开挖间的相互扰动影响较小，应力扰动“叠加效应”不明显；而当左右线同时开挖时，开挖面最小屈服接近度为0.144 4，扰动率为42.67%；即当双线隧道纵向开挖间距较小时，施工扰动很容易引起岩体屈服，开挖面稳定性较差；因此在双线隧道施工中应选定合理的纵向开挖间距，保证施工安全性。

随着纵向间距的变化，监测断面处先行隧道开挖面土体变形(y向)如图9所示。不同纵向间距下开挖面纵向变形规律基本相同，拱顶位置发生的变形最大，拱底位置变形很小；在隧道中心线位置附近变形有一定的突变，开挖面上部产生较大变形且变形沿埋深方向变化率较大，而下部变形较少且变形沿埋深方向变化率较小。综上可知，土压平衡盾构隧道施工时开挖面上部土体易率先发生局部失稳破坏。

图9 监测断面处先行隧道开挖面变形位移曲线

变形是对岩体应力状态改变的宏观表现，如图9所示，随着双线隧道纵向开挖间距的减小，开挖面的变形逐渐变大，隧道开挖对开挖面的应力扰动更加明显。当纵向间距大于48 m时，先行隧道开挖面最大变形(y向)在-11.337～-10.311 mm，差异性较小，说明此工况下后行隧道开挖对先行隧道开挖面的岩体扰动影响不明显。基于开挖面最小屈服接近度和开挖面变形规律，得到双线隧道不同纵向间距下后行隧道对先行隧道开挖面的扰动影响规律基本相近。

3.3 开挖面极限支护压力分析

根据稳定性理论，现以支护压力发生变化情况下，开挖面中心点水平位移发生明显突变时的支护压力作为开挖面的极限支护压力[16]。且模拟中支护压力为梯形荷载，因此取中心点处的支护压力值表示开挖面支护压力，并利用文献[16]中定义的支护压力比λ来表示开挖面支护压力大小。针对监测断面，设不同工况下先行隧道开挖至监测断面时左右线盾构处于停机状态，而后保持后行隧道开挖面支护压力不变，逐级调整先行隧道开挖面支护压力比，并进行一定时间的流固耦合计算，从而得到不同工况下先行隧道开挖面支护压力比与开挖面中心点处水平位移的关系曲线如图10所示。

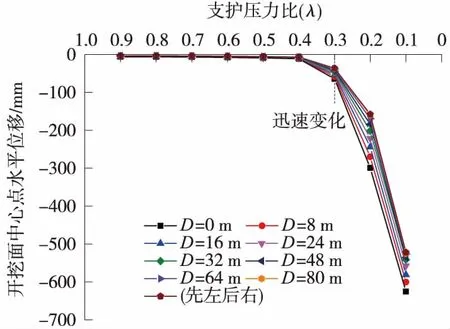
图10 不同支护压力下先行隧道开挖面中心点水平位移

由图10可知，同一工况下，随着支护压力比的减小，先行隧道开挖面中心点处水平位移逐渐增大；当支护压力比大于0.4时，中心点水平位移变化很小；当支护压力比在0.4～0.3范围时，中心点水平位移有一定的增加，位移曲线斜率有一定程度的增大；当支护压力比小于0.3时，中心点水平位移迅速增加，位移曲线斜率较大。且当支护压力比在0.3～0.25，中心点水平位移曲线发生明显突变，不同工况下突变点位置差别不大；根据极限支护压力的定义，以开挖面中心点位移发生明显突变时的支护压力作为极限支护压力，可知不同纵向开挖间距下先行隧道开挖面的极限支护压力差别不大。根据文献[10]，开挖面中心点位移的变化规律反映了开挖面土体应力状态的变化；而由图10知，当开挖面支护压力小于极限支护压力时，不同工况下中心点水平位移的差异性明显，随着纵向间距的减小，中心点水平位移越大；即说明随着纵向间距的减小，后行隧道开挖对先行隧道开挖面的应力扰动越显著。