地形复杂三维地质模型下围岩的蠕变特性研究
2018-11-22张益瑄林文凯晏启祥朱洪雪
张益瑄,林文凯,晏启祥,朱洪雪,刘 阳
(西南交通大学交通隧道工程教育部重点实验室,成都 610031)
近些年来,随着我国在交通隧道领域和地下工程建设方面的不断发展,TBM法具有环保、掘进速度快等优点,在许多地下工程中被采用,而在TBM法施工过程中,围岩蠕变对隧道开挖的影响越来越大,已经成为不可忽视的因素,近些年来,许多的学者研究了围岩蠕变对隧道开挖的影响[1-9],蔡燕燕等[10]考虑围岩蠕变的全过程,推导出了深埋隧洞非线性位移解,侯公羽等[11]在支护反力变化条件下提出被动支护反力连续变化下的迭代算法,并且结合工程实例对围岩的蠕变变形进行了分析。林文凯等[12]基于Burgers的蠕变模型对圆形隧道的内力进行了研究,对比分析了地层结构模型与荷载结构模型两种分析方法,并得出了地层结构模型分析更为有效的结论。王明年等[13]基于有限元的分析方法,结合二郎山隧道的工程实例,分析了高地应力软岩隧道的蠕变特性。同时,也有不少学者在蠕变位移方面进行了研究,余东明等[14]为了描述深埋圆形隧道的开挖支护,基于Burgers与Drucker-parger组合的黏弹塑性模型,推导出了深埋圆形隧道考虑剪胀性能的围岩蠕变位移解析解,结合实际算例,分析了围岩剪胀力与支护反力对深埋圆形围岩蠕变位移的影响规律。
目前在国内,基于Burgers本构模型,利用有限元分析软件ANSYS等建立荷载结构模型和地层结构模型,分析围岩蠕变作用下隧道衬砌结构的内力的研究已经很多,本文做进一步研究分析,建立地形复杂,地表崎岖不平的三维地质模型,在初始应力作用下,实施隧道开挖数值模拟,以隧道开挖模拟的结果为基础,分析在围岩蠕变作用下,支护结构拱顶、拱底及左右拱腰处的位移变化,从而得到围岩的蠕变特性。
1 围岩蠕变理论
综合国内外的岩体蠕变理论研究,目前常用组合模型的方式来模拟岩体的流变关系。组合模型的基本原理是根据岩体的弹性、塑性及黏滞性质来设定一些基本元件,通过这些基本元件的串并联组合,以求能够反映岩体的本构关系,并以此模拟岩体的应力-应变关系。常用基本元件基础上组合的模型有:麦克斯韦体(Maxweii)模型和开尔文体(Keivin)组合模型,以及由M体和K体串联所组合的伯格斯(Burgers)(M-K)体组合模型[6]。结合高黎贡山隧道所处的砂岩层地段开展研究,根据地层岩性特点,选用黏弹性Burgers蠕变模型开展隧道围岩蠕变分析。Burgers模型的本构方程为
σ+p1σ1+p2σ2=q1ε1+q2ε2
(1)
式中,E1、η1分别为Maxweii模型的弹性模量、黏滞系数;E2、η2分别为Keivin模型的弹性模量、黏滞系数;σ1、σ2分别为正应力对时间的一阶、二阶导数;ε1、ε2分别为正应变对时间的一阶、二阶导数。由于Burgers模型的4个参数不能作为Prony级数输入值,因此需将E1、E2、η1、η2转化为剪切模量的Prony级数参数[15]。对于Burgers模型,Prony剪切模量表达式为[12]
(2)
式中,g∞为松弛时间无限大时的剪切模量;g1,τ1分别为Maxweii模型的相对剪切模量和松弛时间;g2,τ2分别为Keivin模型的相对剪切模量和剪切时间;G0为松弛时间为0的剪切模量。
将Burgers模型中的弹性模量系数进行转换,并将获得的表达式进行拉普拉斯变换和拉普拉斯逆变换,便可以得到剪切模量的Prony级数表达式,通过对比式(2),便可得到Burgers模型在ANSYS中需要的4个Prony级数g1,g2,τ1,τ2[16-17],可用于下文的蠕变分析。
2 三维地质模型与应力场回归方法
建立高黎贡山隧道砂岩层地段三维地质模型。为了模拟地形复杂,地表崎岖不平的模型,结合地质平面图中的等高线资料,导入CAD中得到dxf文件,然后用GoCAD软件调用dxf文件,提取等高线上的相关拟合点坐标数据。由于数据的不均匀性,为了便于这些提取数据在ANSYS中建模,借用Surfer软件使数据均匀化,使数据达到均匀值,然后将处理后的数据导入ANSYS中,就可以得到地形复杂,崎岖不平的三维地形地质模型。结合高黎贡山实际条件,建立三维地质山体模型,模型下部是一个长方体模型,长、宽、高尺寸为250 m×150 m×120 m,在山体下部模型中包含有隧道衬砌结构模型,其中模型下部位置进行隧道开挖模拟,衬砌的内、外半径分别为4、4.5 m。从而获得ANSYS分析的整体模型如图1所示。

图1 数值模型
将围岩视为各向同性连续介质,隧道围岩、衬砌力学参数见表1。

表1 周围土体与衬砌参数
围岩蠕变参数分别为:Maxweii模型的弹性模量、黏滞系数分别为E1=5.546 GPa,η1=32.697 GPa·h,E2=3.211 GPa,η2=2.378 GPa·h,由前面公式可得到4个Prony级数,分别为g1=0.118 2,g2=0.883 6,τ1=17.265 4,τ2=0.267 6。
地应力场是隧道从开挖到支护等仿真分析的计算基础,对合理进行地下工程设计与施工具有很大的现实意义[16-17],初始地应力场也是影响隧道围岩稳定性的重要影响因素[18],以现场部分实测地应力数据为基础,同时考虑地形、地质方面的因素,结合理论研究与数值分析进行反演[19-20]。本文考虑用多元线性回归分析法对高黎贡山隧道砂岩层地段进行初始地应力回归。

(3)

为了方便统计与计算,取m个相关点,由最小二乘法残差平方和的方法得到
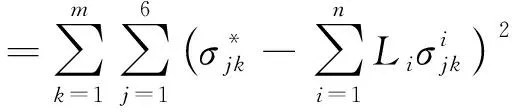
(4)

由最小二乘法的基本原理,可以得到回归系数,为使得S残最小,令S残对Li的偏导数为0,即
(5)
整理后可以得到如下矩阵
(6)
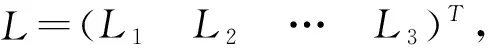
(7)
j=1,2,3,…,6表示6个初始应力分量。
山体原地应力测试孔CS1、CS2分别位于模型x=40 m,y=75 m和x=140 m,y=75 m两处附近,两应力测试孔的实测数据如表2所示,其中数据已转化为模型坐标方向的应力分量。
进行初始地应力场的反演,分别对该复杂地形三维模型施加构造应力场,应力场1、3分别为YZ面挤压应力场与竖向的剪切应力场,应力场2、3、5分别为XZ面的挤压应力场,水平与竖向剪切应力场。
用相关软件分别计算上述各构造应力场和自重应力场,可以得到相关点深度的应力分量值,以表2实际测量得到的应力值为基础,代入式(3)~式(7)进行分析,计算可以得到该处围岩在上述假设各构造应力场下的初始状态,具体如式(8)回归方程
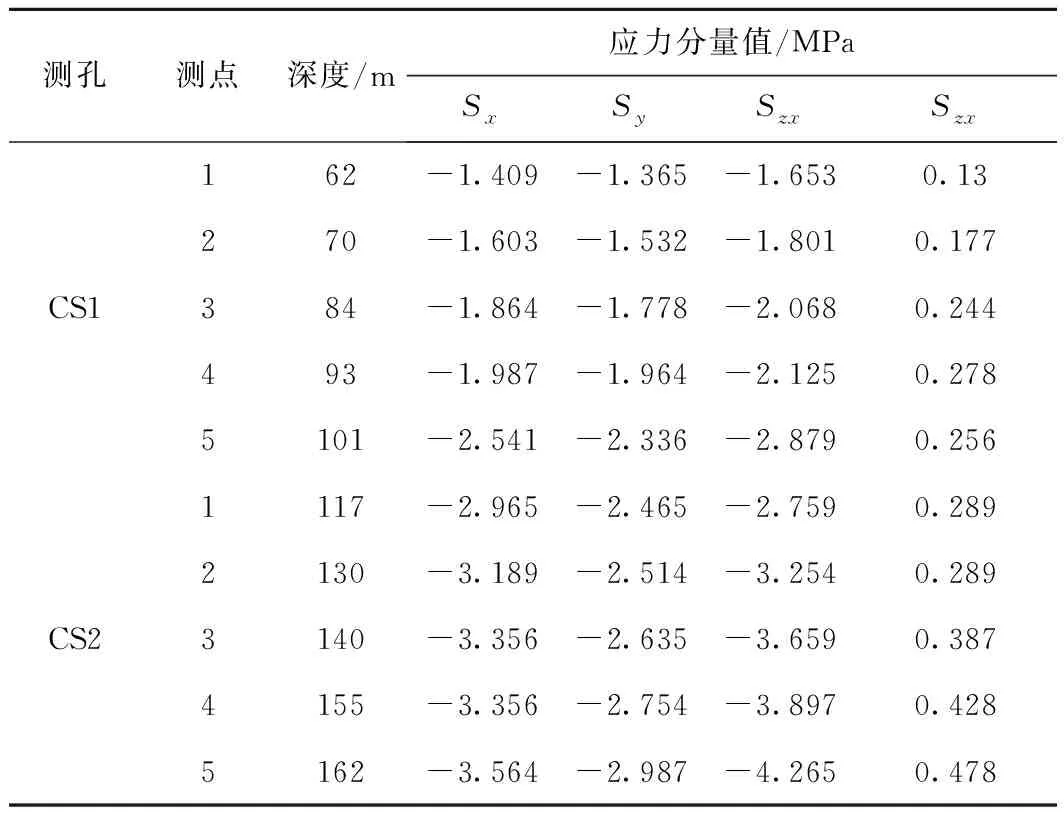
表2 测试孔应力分量
σ=1.073σ自重+6.374σ构1+1.628σ构2+
42.336σ构3+0.433σ构4+0.245σ构5
(8)
σ构1、σ构2、σ构3、σ构4、σ构5、σ自重分别对应5个构造应力场和自重应力场。对该处山体的回归效果进行分析,可以计算得到该处山体的初始应力场回归方程的相关系数r=0.964,接近于1.0。残差平方和S残=12.687,说明初始地应力场回归具有较好的相似度。
3 结果分析
3.1 复杂地形下构造应力场
运用多元线性回归法进行分析,得到山体在构造应力场以及自重应力场下的回归方程,以式(8)和相关数据为基础,可以得到相应的边界条件,运用有限元软件分析,复杂地形下山体地层的竖向位移和竖向应力如图2、图3所示。
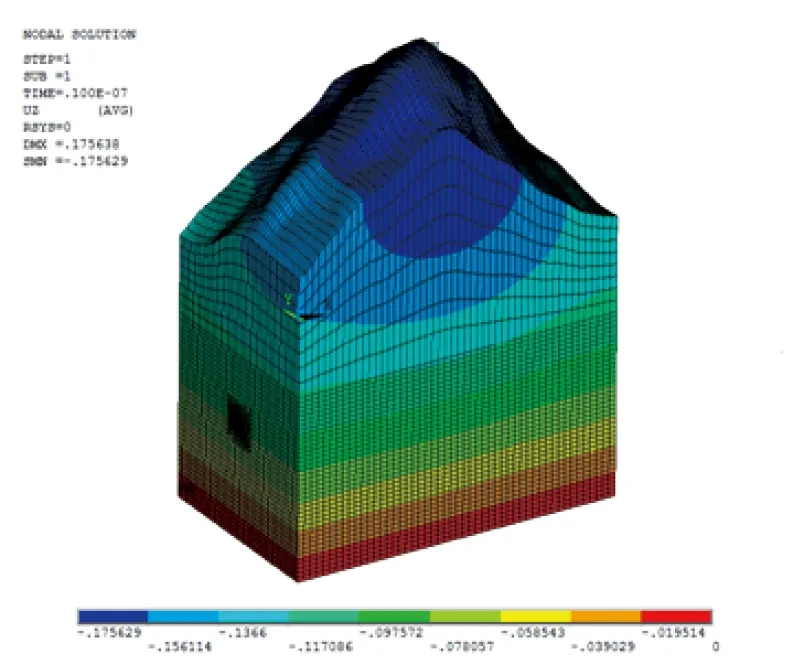
图2 初始地层竖向位移云图(单位:mm)
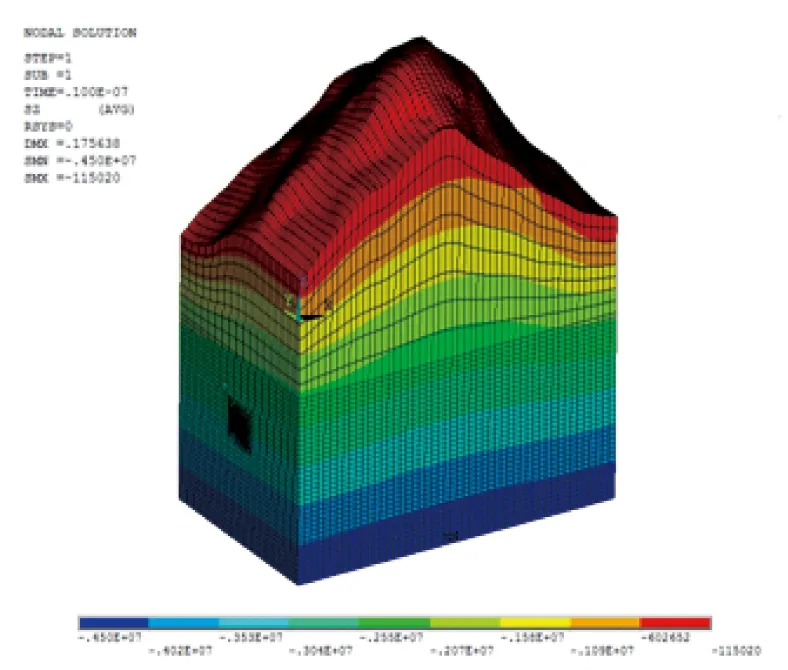
图3 初始地层竖向应力云图(单位:Pa)
由图2和图3可知,受到山体地形复杂、崎岖不平的影响,山头地表处有较大的初始竖向位移,且在底层位置山体有较大的初始竖向应力。
3.2 隧道开挖支护状态
为了得到复杂地形下隧道开挖后的支护状态,用有限元软件进行隧道开挖数值模拟,在上文假定的构造应力场与自重应力场作用下,隧道开挖完支护结构的竖向位移云图见图4。

图4 隧道开挖支护衬砌竖向位移云图(单位:mm)
从图4可以看出,受到山顶复杂地形的影响,隧道纵向的中部范围内竖向位移较大,在隧道顶部按照梭形分布,在靠近隧道两端的位置,竖向位移逐渐趋于平缓,这种分布与图2初始地层竖向位移较为类似。
隧道开挖支护结构竖向应力云图如图5所示。

图5 隧道开挖支护衬砌竖向应力云图(单位:Pa)
由图5可以看出,隧道顶部沿纵向有较大的应力分布,且应力分布比较均匀,隧道顶部的应力分布与山头处的应力分布较为相似。
3.3 围岩蠕变下支护结构行为分析
下文研究地形复杂三维地质模型下,隧道开挖后,围岩的蠕变对支护结构的影响。为了更好地得到结果进行分析,在建模过程中,取隧道模型的纵向长度为300 m,在模型的纵向方向,分别选取位置不同,埋深不同的5个数值采集面,并按照顺序进行编号,数值检测断面的位置与埋深见表3。

表3 各数值采集断面分布
其中,断面1和断面5位于模型纵向的两侧,位置上位于隧道埋设较浅处,断面2、断面3、断面4位于模型纵向中部,相对于断面1、断面5,埋深较大。各数值采集断面分布如图6所示。
支护结构的拱顶部位也设置相应隧道纵向的数值采集断面,各支护结构数值采集断面示意见图6。支护结构横断面监测点布置见图7,如监测断面2的拱顶为A2,拱底为B2,左侧拱腰为C2,右侧拱腰为D2。

图6 数值监测点断面示意

图7 监测点横向示意
以5个隧道横向数值采集断面和隧道纵向数值采集断面的数据为基础,分析研究隧道在围岩蠕变荷载作用下,支护结构的响应特点。
3.3.1隧道各监测断面Ai处的位移
以隧道5个横向数值采集断面支护结构Ai处位移随围岩蠕变变化的数据为基础,得到Ai处位移随时间变化的趋势如图8所示。

图8 隧道各数值采集断面Ai位移曲线
由图8可知,在围岩蠕变荷载作用下,位于隧道中部的断面2、断面3、断面4横向数值采集断面的Ai处位移不断增加,而位于隧道两端的1、5数值采集断面随着时间的增加位移不断减小。
图8中,围岩蠕变产生的初始阶段,A3处沉降为38.71 mm,是产生最大沉降位置,A1处沉降为28.87 mm,是所有拱顶位置处的最小沉降值,这与在初始应力场作用下支护结构的位移分布是相似的,因为A3相比于A1埋深较大。由于A1相对于A5有更大的埋深,A1处的位移减小率更大,在断面2、断面3、断面4中,在围岩蠕变作用下,可以发现A3处位移增加的速率是最快的,原因是断面3相对于其他断面埋深较大。
3.3.2隧道各数值采集断面Bi处的位移
通过对5个横向数值采集断面得到的数据进行汇总分析,得到B1处位移随时间变化的趋势如图9所示。
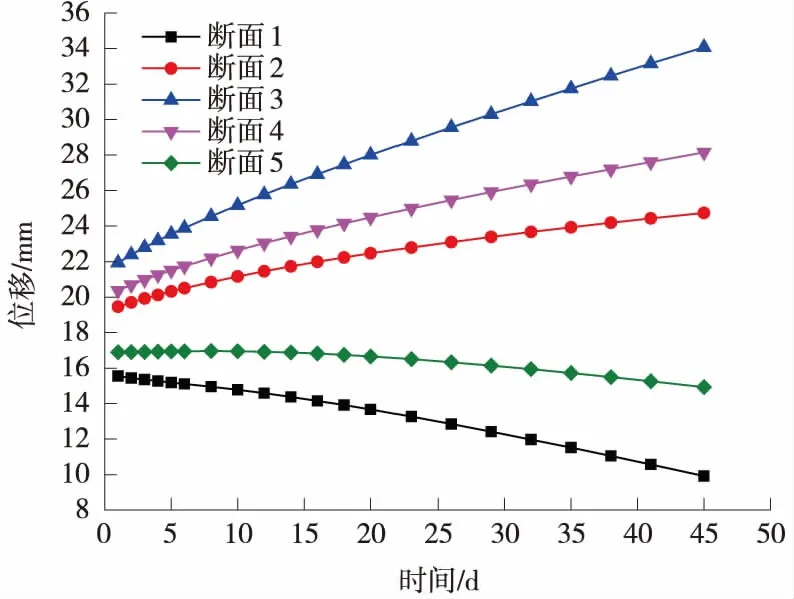
图9 隧道各数值采集断面Bi处位移曲线
由图9可知,受到蠕变荷载的影响,1与5数值采集断面支护结构Bi的位移随着天数增加不断减小, 隧道断面2、断面3、断面4横向数值采集断面的B1处位移是不断增加的。Bi处的位移变化趋势与Ai处的位移变化趋势是类似的。
在图9中,围岩蠕变产生的初始阶段,B3处位移的大小为22.01 mm,是产生位移的最大位置,B1沉降为15.98 mm,是所有拱顶位置处沉降的最小值。同时可以发现,在断面2、断面3、断面4中,断面3拥有较大的埋深,因此A3处位移最大,在2、3、4断面中,在围岩蠕变随时间作用下,埋深越大的位置处的位移增长速率也越大。
3.3.3隧道各监测断面Ci与Di的收敛位移
通过对5个横向数值采集断面得到的数据进行汇总分析,得到Ci与Di的收敛位移随时间变化的趋势如图10所示。

图10 隧道各监测断面Ci与Di的收敛位移曲线
由图10可以看出,隧道横向数值采集断面2、断面3、断面4随着时间增加,左右拱腰收敛位移呈减小趋势,其中埋深较大的断面3处收敛位移减小最大,断面1和断面5处左右拱腰收敛位移呈现增大趋势,由于断面1和断面5埋深接近,增长趋势也较为接近。在围岩蠕变作用下,通过对比分析Ai与Bi处的位移,可以发现Ci与Di之间的收敛位移的变化趋势与拱顶和拱底处的位移变化趋势恰好是相反的。
在图10中,围岩蠕变产生的初始阶段,Ci与Di位置的收敛位移4.62 mm是收敛位移最大值处,相对地,C3与D3位置的收敛位移大小为3.89 mm,是收敛位移的最小值处。由图中各曲线的变化趋势,在围岩蠕变的作用下,随着断面埋深的不断增大,相应左右拱腰的收敛位移不断减小,与上述各断面Ai、Bi处位移随蠕变变化相比,Ci与Di位置的收敛位移数值变化幅度较小,并且变化的数值也比较小。
3.3.4 隧道纵向各数值采集断面拱顶位移分析
为了具体分析研究纵向拱顶位移随蠕变的变化趋势,这里沿着隧道的纵向方向,在拱顶位置取一系列采集点,采集点的范围为10~240 m,每隔10 m共取24个点,研究蠕变作用天数下位移的变化趋势,结果如图11所示。
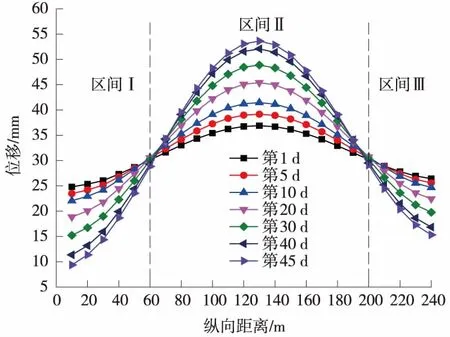
图11 隧道横向数值采集断面拱底位移曲线
结合图11进行分析,在地形崎岖复杂的山体中间部位,沿着隧道纵向进行分析,相对埋深较大处,支护结构的拱顶位移大于山体两边处的拱顶位移。随着围岩蠕变作用不断增加,将图11根据变化趋势分为3个区间,其中区间I,在隧道纵向x=10 m到x=60 m范围内,支护结构拱顶位移随着蠕变时间的增加不断减小;区间Ⅱ,沿隧道纵向区间x=60 m到x=200 m,支护结构拱顶位移在蠕变荷载作用下,随着时间是不断增加的;区间Ⅲ,沿隧道纵向区间x=200 m到x=240 m范围内,随着荷载作用时间的增加,拱顶位移不断减小,区间Ⅱ范围内形成了一个拱形曲线,观察图2发现,支护结构拱顶位移随着时间逐渐形成一个山头,与地形崎岖复杂的三维地质模型的地表形状是类似的。
其中,区间Ⅰ处的拱顶位移随着蠕变时间增加,变化幅度大于区间Ⅲ的位移变化,在图11中表现为区间Ⅰ处的曲线比区间Ⅲ的曲线更为稀疏,在三维地质模型中表现为区间Ⅰ处的地表地形更加复杂陡峭。
3.3.5同一数值采集断面下支护结构位移随时间变化分析
为了研究围岩蠕变对支护结构的响应,选取上文的5个监测断面,分别提取它们在Ai,Bi处的位移以及Ci,Di两处的收敛位移进行分析。
数值采集断面1支护结构的位移随时间变化如图12所示。
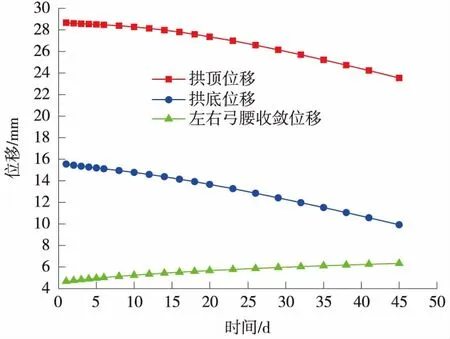
图12 数值采集断面1支护结构位移曲线
由图12可以看出,数值采集断面1在整个蠕变分析过程中,拱顶处的位移要大于拱底处的位移,拱顶处和拱底处的位移都随蠕变时间的增加而减小,但减小的速率不断增大,左右拱腰处的位移随时间缓慢增加,增加速率较为稳定。
数值采集断面3支护结构的位移随时间变化曲线如图13所示。
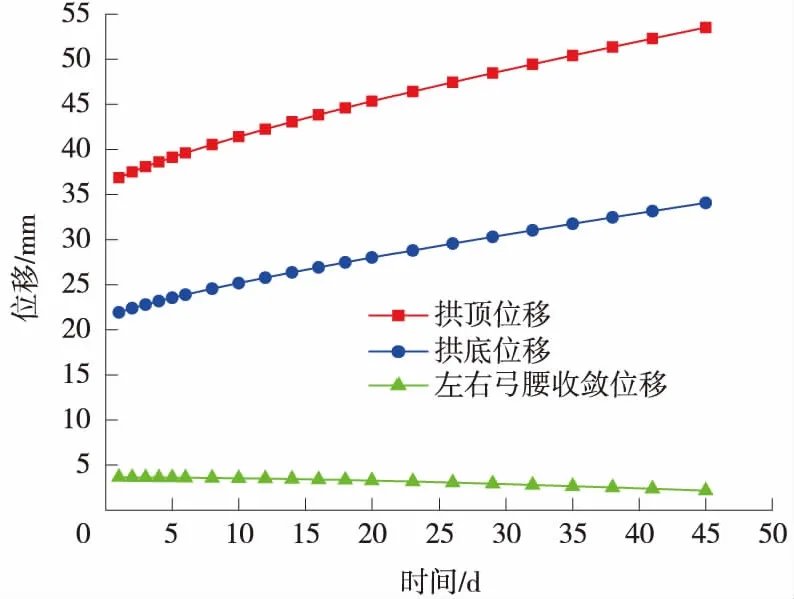
图13 数值采集断面3支护结构位移曲线
由图13可以看出,数值采集断面3在蠕变时间增加的过程中,拱顶的位移要大于拱底的位移,拱顶和拱底位移是不断增加的,增加的趋势较为稳定,而左右拱腰的位移随蠕变时间增加不断减小,整体上监测断面3左右拱腰的位移较小。
数值采集断面5支护结构的位移随时间变化如图14所示。

图14 数值采集断面5支护结构位移曲线
由图14可以看出,在蠕变时间增加的过程中,拱顶位移数值要大于拱底位移,但拱顶位移和拱底位移都随时间不断减小,左右拱腰位移随蠕变时间呈平缓增加的趋势。
4 结论
通过建立地形复杂,崎岖不平的三维地质模型,在初始应力作用下,实施隧道开挖数值模拟,分析隧道开挖模拟后在围岩蠕变作用下,支护结构不同部位的位移变化,对支护结构5个横向数值采集断面的Ai,Bi,Ci,Di处,以及1个纵向数值采集断面进行相关数据提取,从而得出以下结论。
(1)在山体中间部位,支护结构的拱顶Ai处的位移在蠕变荷载作用下,位移随时间变化的趋势是不相同的,其中,埋深相对较浅的断面A1和A5处拱顶位移在围岩蠕变荷载作用下,位移呈逐渐减小的趋势,而位于隧道中部的A2,A3,A4随着蠕变时间的增加,位移不断增大,原因是上述3个断面埋深相对较大。
(2)支护结构Bi处的拱底位移受到围岩蠕变荷载的影响,随着时间的增加,Bi处的位移变化趋势类似于Ai处的拱顶位移变化,同时Bi处的位移数值要小于Ai处。
(3)Ci与Di之间的收敛位移的变化趋势也随着断面位置的变化而不同,其中C2与D2,C3与D3,C4与D4之间的收敛位移在蠕变荷载作用下,随时间呈现减小的趋势,C1与D1,C5与D5之间的收敛位移则随着时间的增大不断增大。
(4)通过分析同一数值采集断面下支护结构位移随时间变化曲线,发现拱顶处与拱底处的位移变化趋势类似,左右拱腰处的收敛位移变化趋势相反,位于隧道两端的断面1和5各位置的位移变化趋势是相似的,而位于中部的数值采集断面各位置处则与两端位置有着相反的变化趋势。
