波形片特性仿真及其疲劳可靠性分析＊

严正峰 段亚林 全世平

（1.合肥工业大学，合肥 230009；2.合肥工业大学 智能制造技术研究院，合肥 230009）

主题词：波形片 分离特性 疲劳可靠性 载荷-位移特性

1 前言

离合器的作用是传递发动机扭矩，并在起步和换挡时切断动力、减缓传动系统冲击等[1]。为减缓离合器在结合与分离过程中沿轴向产生的冲击，要求从动盘具有良好的轴向弹性，而波形片是从动盘中关键性的受力部件之一，其非线性“载荷-位移”弹性曲线对离合器扭矩传递有重要影响，因此对波形片轴向压缩特性的研究对改善汽车换挡品质等具有实际意义。

国内外学者对波形片进行了相应研究，如Vasca F等[2]阐述了波形片的弹性特性对于输出扭矩的影响；Sfarni S等[3]通过数值分析方法对不同结构波形片的弹性特性进行了研究，并分析了如何利用波形片表面接触压力分布预测摩擦片磨损情况；Cappctti N等[4]对波形片弹性特性对于自身主要几何参数的敏感程度进行了分析，并研究了温度变化对于波形片载荷-位移特性曲线的影响。

本文在前人研究的基础上，构建了典型汽车从动盘总成波形片三维模型和有限元模型，分析了波形片轴向压缩特性及其疲劳寿命，为改进离合器波形片的设计提供理论参考。

2 从动盘总成及波形片轴向压缩特性

2.1 从动盘总成结构

从动盘总成结构见图1。波形片为整体式，材料为65Mn，沿半径方向开槽，在外缘部分呈现出许多具有波浪形状的扇形结构，如图2所示。

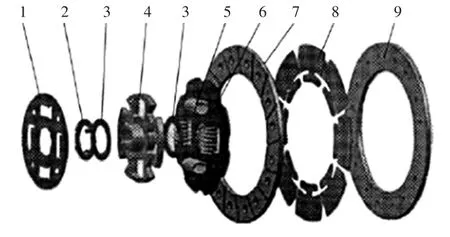
图1 从动盘总成结构

图2 整体式波形片

2.2 波形片轴向压缩特性

在摩擦片压缩波形片的过程中，波形片会发生周向伸展变形，波形片与摩擦片有效接触面积的变化量与波形片轴向伸缩量之间呈非线性关系，使得波形片有一个非线性的轴向压缩特性，且随压缩行程的增加，波形片所受到的载荷先缓慢增加之后再迅速增加，如图3所示。

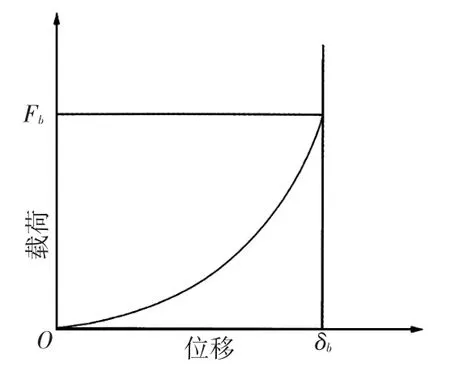
图3 波形片轴向压缩特性

3 波形片特性的理论计算

波形片可以简化为3个部分，与摩擦片表面接触部分及非接触部分（左右两部分）[5]，如图4所示。波形片与摩擦片表面接触部分为平面，可不考虑其弹性变形，波形片左右两侧与摩擦片表面非接触部分可假设为悬臂板，依据力学公式可推导出其变形与载荷的关系。

图4 波形片简化图及力学模型

采用自然坐标并利用Euller-Bernoulli方程建立悬臂板的挠曲方程：

式中，D=D(s)为抗弯刚度，s为固定端到自由端的距离；θ为转角；M(s)为大挠度分析时任一截面的弯矩；E为弹性模量；t为厚度；b为宽度；μ为泊松比；F为所承受的载荷；H为自由端到s点的水平距离（即悬臂板的力臂）。

对式（1）～式（4）处理后得：

通过式（5）可求得θ与s的关系，再根据式（6）可得出波形片自由端的挠度w。

根据式（6），依据设定好的载荷值即可求出波形片自由端的挠度w，再经过对扰度值的修正即可得出波形片的轴向压缩特性。

4 波形片特性仿真分析

4.1 实体模型建立

本文所研究的整体式波形片由10个叶片组成，每个叶片厚度为0.8 mm，因每个叶片几何尺寸、材料及加工方法完全一致，因此假设10个叶片具有相同的载荷-位移特性，并取其中1个叶片进行建模。考虑到实际工作过程中只有叶片波浪形部分提供轴向弹性刚度，因此只针对波形部分进行建模分析，其三维实体模型如图5所示。

图5 单个叶片波形部分实体结构模型

4.2 有限元模型建立

波形片的材料如表1所列。为了模拟波形片实际工作状况，建立了两个摩擦片的三维模型，并与波形片组成装配体后导入有限元分析软件workbench中。定义上、下两个摩擦片为刚体，将各材料参数输入有限元分析软件并采用四面体进行网格划分，定义波形片网格大小为0.6 mm。依据从动盘总成的实际工况设定约束为：下摩擦片固定；波形片铆接孔处具有沿Z轴方向移动自由度；上摩擦片沿Z轴负方向移动0.7 mm，如图6所示。图7为最后得到的波形片有限元仿真模型（为方便观察隐去上摩擦片）。

表1 波形片材料参数

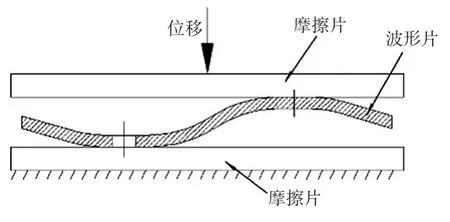
图6 波形片模型边界条件示意

图7 波形片数值仿真模型

4.3 波形片轴向压缩特性

对上摩擦片施加时间序列载荷谱（载荷为位移载荷），设定自动调节子步数，通过有限元仿真分析可得出每个子步对应的波形片轴向位移及与之对应的波形片轴向载荷，经数据处理可得波形片载荷与轴向压缩位移之间的关系[6]，如图8所示。从图8可看出，波形片所承受载荷与位移之间呈非线性关系。

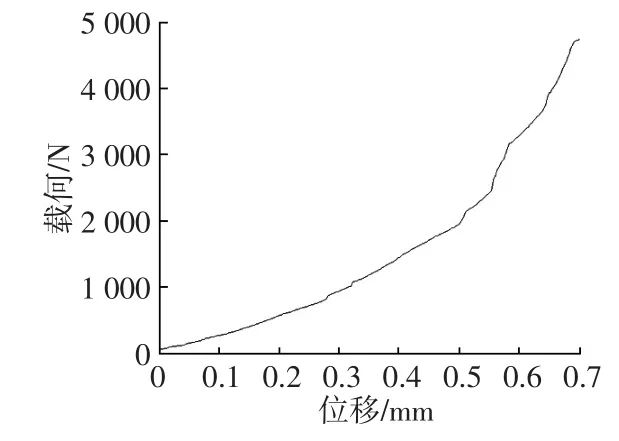
图8 波形片载荷-位移特性曲线仿真结果

5 波形片的疲劳可靠性分析

5.1 静力学分析

根据上述的边界及约束条件，采用位移时间载荷步的加载方式，利用ANSYS workbench软件获得的波形片应力云图如图9所示，从图9可看出，在波形片轴向压缩0.7 mm的过程中，最大应力发生在波形片波形翘曲位置，为840.2 MPa。

图9 波形片应力云图

5.2 载荷谱定义

载荷谱的准确定义对疲劳分析结果的准确性具有很大影响。本文采用的时间步载荷谱其时长为1 s，在1 s时长内上摩擦片沿Z轴负方向位移0.7 mm，将波形片逐渐压平，载荷子步为318步。

5.3 波形片材料S-N曲线

以材料的S-N曲线为基础，通过名义应力法对波形片进行疲劳寿命分析。将材料参数（65Mn的屈服强度785 MPa、抗拉强度980 MPa）输入疲劳分析软件ncode中，生成S-N曲线，由于受加工及零件外形影响，零件与标准试件S-N曲线会有一定误差，所以需要对所得S-N曲线进行修正[7]，修正后S-N曲线如图10所示。

图10 修正后的S-N曲线

5.4 疲劳可靠性分析

将静力学计算结果导入疲劳分析软件nCode Design Life中，通过求解得到波形片的寿命云图，如图11所示。

图11 波形片寿命云图

由图11可知，波形片损伤较严重的区域位于波形片的波形翘曲部分，这与有限元分析结果相吻合，而波形片在实际使用过程中的破坏部分也集中在此位置，该分析结果表明波形片能够达到疲劳寿命要求。

6 试验验证及分析

6.1 波形片轴向压缩特性的试验验证

在从动盘总成轴向压缩特性试验机上进行波形片轴向压缩特性试验，仿真与试验结果对比如图12所示，表2为在相同位移量时通过仿真分析（FE）与试验测量（EP）获得的相应轴向载荷值误差对比结果。

图12 波形片轴向压缩特性仿真结果与试验结果

表2 轴向载荷误差分析结果

从图12可看出，仿真结果与试验结果的轴向压缩特性曲线近似吻合；由表2可知，当波形片压缩位移分别为0.1、0.3、0.5和0.7 mm时，仿真与试验获得的波形片轴向载荷之间的最小误差为7.1%，最大误差为9.9%，在工程应用可接受范围内。导致产生误差的主要原因为：仿真模型与实际产品几何尺寸之间存在差别；仿真模型采取了简化处理；实际仿真分析中波形片与摩擦片之间非线性接触参数难以准确建立等。

6.2 波形片疲劳试验验证

在从动盘总成轴向压缩耐久试验机（图13）上进行波形片疲劳寿命试验，经5.0×105次轴向压缩试验后，再通过波形片轴向压缩特性试验机检测其轴向压缩特性，绘制轴向压缩特性曲线，如图14所示。

图13 从动盘总成轴向压缩疲劳耐久试验机

图14 波形片轴向压缩特性曲线

经过疲劳耐久试验后，从外观上没有发现波形片产生疲劳裂纹和破裂，并且轴向压缩特性依然能够满足要求，这表明该波形片疲劳可靠性满足要求。

7 结束语

本文以离合器从动盘波形片为研究对象，分别建立了波形片轴向压缩特性数学分析模型和有限元分析模型，通过仿真分析得到其载荷-位移特性曲线。进一步对波形片进行了疲劳可靠性分析，结果表明其寿命能够满足要求，并通过与试验数据的对比验证了仿真分析的可靠性。本文的研究为离合器产品开发设计提供了参考依据，且有利于节约成本、缩短离合器产品开发周期。