《绝对值不等式的解法》教学设计

石 鹏，刘 卓

（1.西安交通大学附属中学，陕西 西安；2.西安交通大学附属中学航天学校，陕西 西安）

一、复习引入

在初中我们学习过绝对值的定义及几何意义，首先请同学们回忆一下

（2）绝对值的几何意义：

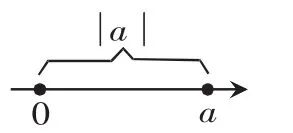
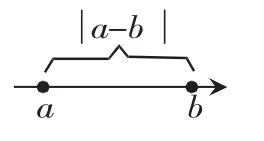
二、新课探究

方法一：利用绝对值的几何意义解不等式

方法二：利用绝对值的定义去掉绝对值符号，需要分类讨论

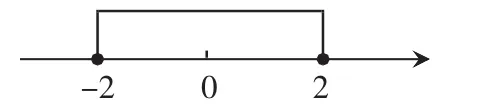
①当x≥0 时，原不等式可化为x＜2，所以 0≤x＜2；

②当x＜0 时，原不等式可化为-x＜2，所以-2＜x＜0；

综合①②得，原不等式的解集为{x│-2＜x＜2}

方法三：两边同时平方去掉绝对值符号

原不等式的解集为{x│-2＜x＜2}

方法四：利用函数图象求解集

原不等式的解集为{x│-2＜x＜2}

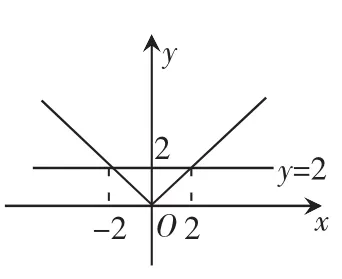
方法一：利用绝对值的几何意义解不等式；

方法二：利用绝对值的定义去掉绝对值符号；

方法三：两边同时平方去掉绝对值符号；

方法四：利用函数图像求解集；

∴x≤1 或x≥4。解集为{x│x≤1 或x≥4}

解集为：{x│x＜-1 或-1＜x＜3 或x＞5}

解绝对值不等式的思路是转化为等价的不含绝对值符号的不等式（组），常见类型有：

解绝对值不等式的基本思想是去绝对值符号，通过下面例题一起研究此类型解法。

方法一：利用绝对值的几何意义求解。

解：如图，数轴上-2，1 对应的点分别是A，B，-3，2 对应的点分别是A1，B1，

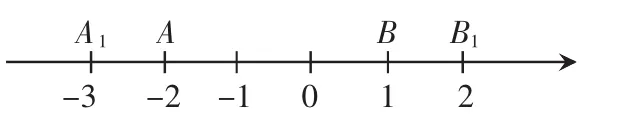
所以数轴上在A1和B1之间的任何一个点到A，B之间的距离都小于5；

数轴上在A1的左边或在点B1的右边的任意一个点到A，B之间的距离都大于5。

解集为：{x│x≤-3 或x≥2}。

总结：这种方法体现了数形结合的思想。

解：当x≤-2 时，等价于：（1-x）-（x+2）≥5，所以x≤-3，

当-2＜x≤1 时，等价于（1-x）+（x+2）≥5，即：3≥5，解为 Φ。

当x＞1 时，等价于（x-1）+（x+2）≥5，所以，x≥2。

解集为：{x│x≤-3 或x≥2}。

总结：这种方法体现了分类讨论的思想。

方法三：通过构造函数，利用函数图象来求解。

解：原不等式等价于：（x-1）+（x+2）-5≥0，

做出函数的图象（如右图），函数的零点为-3，2，

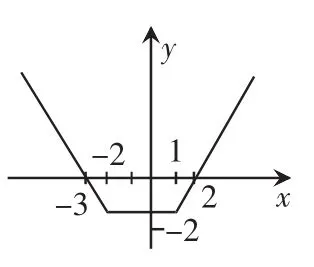
由图象可知：当x≤-3或x≥2时，y≥0。解集为：{x│x≤-3 或x≥2}。

总结：这种方法体现了函数与方程的思想。

方法一：利用绝对值的几何意义；

方法二：利用各绝对值的零点分段讨论（零点分段法）；

方法三：构造函数，利用函数图象求解．