一题多解在圆锥曲线极值求解中的应用

李晨曦

（洛阳市第一高级中学，河南 洛阳）

在高中数学的学习过程中，往往需要花费大量的时间去做习题，但是数学成绩提高并不明显，题海战术并没有带来想要的结果。于是，有人抱怨，题海战术已经不适应当代孩子们、创新思维已经被禁锢在大量的练习和考试中等。其实，对任何事情的看法都不应以偏概全，客观看待数学学习的题海战术方法，并从中提炼出学习技巧，往往会获得事半功倍的效果。比如，利用发散思维，从不同角度去解决同一个数学问题，即一题多解，久而久之，题海战术就会演变成解题思维的灵活性和创新性。

新课标要求全面培养高中生的思维能力，其途径就是培养其数学思维能力，一题多解是掌握和运用所学基本知识和技能，训练和培养思维的灵活性和创造性的重要途径。由于每个人在解读同一个问题时视角不同、知识运用差异，因此，同一问题可能得到几种不同的解法，这种方法可以让我们多方思考、联想推理以及合理转化，提高数学解题能力和创新思维能力。下面以求圆锥曲线的离心率之和的最大值为例进行阐述。

已知，如下图，F1、F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且，则椭圆和双曲线的离心率倒数之和的最大值为多少？

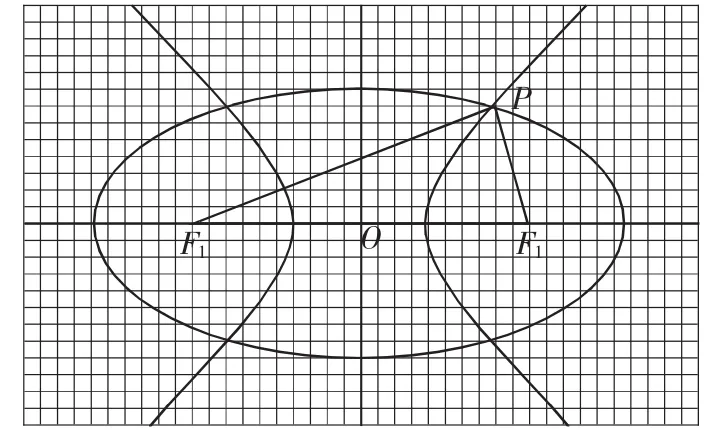
这是一个求极值的问题，以下以三角换元法、向量法、二次函数法以及三角形法进行解答。设椭圆方程为离心率为e1，双曲线方程为，离心率为e2，由余弦定理可得

解法一：三角换元法

利用辅助角公式得：

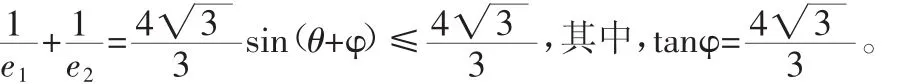
解法二：向量法

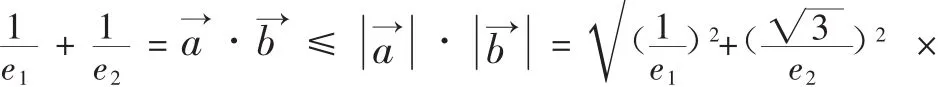
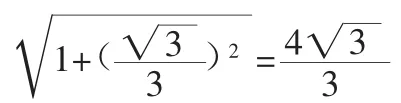
解法三：二次函数法

假设P点在第一象限，且设在△PF1F2中，由余弦定理得

联立①②式可得：

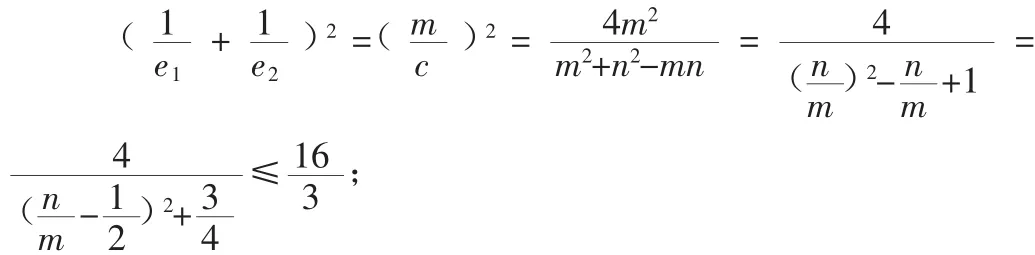
解法四：解三角形法

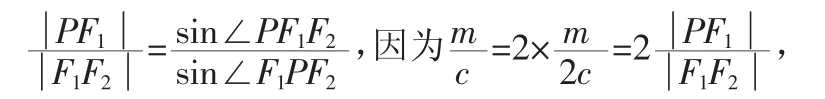
例题中解法一中利用换元法，利用设辅助角减少未知量的个数，利用三角函数求最值；解法二中巧妙利用设置向量，利用向量的定理求解；解法三将问题转化为二次函数求解，解法四利用三角形的正弦定理求解等等，这些想法、技巧都是在日常大量的练习中培养出的逻辑思维。

一题多解激发了我学习数学的兴趣。运用平时积累的做题方法，通过归纳和整理，提炼出属于自己的解题技巧。在解题过程中，既可以获得成就感.还可以有机会将自己的解题方法、解题思路以及解题想法在同学面前展现，获得老师的认可，能清楚地意识到自己在学习中的创造性和自主学习的能力，极大地增强了学好数学的信心，激发了学习数学的热情，同样也能感受到了数学的乐趣。

一题多解强化了我的逻辑思维。心理学研究表明，在解决问题的过程中，如果主体所涉及的不是生硬的模式化问题，那么就需要创造性的思维和技巧，而创造的过程或解决问题的过程即是获得解题技巧。数学问题的解题技巧是指探求数学问题的答案时所采取的途径和方法，利用技巧可以解决其他的数学问题，即学会了“渔”，而不是被动地接受“鱼”。