巧解东风云水意，踏星掬月近天涯<br/>——基于数学对象的高中函数题解构研究

巧解东风云水意，踏星掬月近天涯
——基于数学对象的高中函数题解构研究

2018-11-21袁一丹

新课程(下) 2018年9期

关键词：图象对象方向

袁一丹

（浙江省桐庐中学，浙江桐庐）

一、选题背景

（一）函数处在高中数学核心地位

函数知识贯穿高中数学，与数列、解析几何等知识紧密联系，是高中数学的核心内容，也是历年浙江省高考的重难点（近三年纯粹函数考题的统计见下表，不含其他知识背景考查函数题）。学好函数是学好高中数学的关键，同时是深入研究数学甚至是其他学科的基础。

高考年份题号总分2015文 5（5分）、8（5分）、11（6分）、12（6分）、20（15分） 37分2015理 7（5分）、10（6分）、18（15分） 26分2016 文 3（5 分）、6（5 分）、7（5 分）、11（6 分）、12（6 分）、20（15 分） 42 分2016理 5（5分）、10（6分）、18（15分） 26分2017 5（4 分）、7（4 分）、17（4 分）、20（15 分） 27 分

（二）数学对象确立的适切性是数学解题的关键点

数学解题结构的过程一般可分四环节：定义概念→探究性质→建立联系→实践应用。详细的，首先从数、形的角度提取信息并确立数学对象，然后探索数学对象的要素与要素、要素与环境等之间的关系和相互作用而探究出性质，再建立相关知识的数学联系形成一个知识体系，最后应用所生成的新的知识体系来解决数学问题。这样形成一个螺旋上升、层层深入并能达成深化认识、拓展新知的数学问题解构过程，而其中数学对象确立的适切性是数学问题解构的关键点。

【案例 1】（2008 年浙江理 15）

已知t为常数。函数y=|x2-2x-t|在区间［0，3］上的最大值为2，则 t= .

点析：此题难点是参数t的认识和处理。若通过分析解构出数学对象来开展解题的路径，如确立数学对象为函数y=x2-2x，然后探究y=x2-2x的图象与函数y=x2-2x-t的图象及y=|x2-2x-t|的图象的关系，再建立直观的数学联系，结合图象解决问题。本题本质的解构方法在于能否把问题转化为一个确定函数图象的平移和翻折变换到某一特定位置。

（三）高中生之于数学解题的思维盲点

高中数学语言相比初中数学抽象程度突增，知识内容整体数量巨增，思维方法更具严谨性和推理性，对综合分析能力较弱的学生易产生学困点，解题时更会出现思维盲点。如何从抽象的数学内容中提取出适切的数学对象？如何把抽象的数学对象转化得直观而易于探究？这是我们数学解题研究一个努力的方向。

【案例 2】（2015 浙江理 7）

存在函数f（x）对任意x∈R都有（）

A.f（sin2x）=sinxB.f（sin2x）=x2+x

C.f（x2+1）=|x+1|D.f（x2+2x）=|x+1|

点析：此题难点在于题设信息怎么提取转化，选项信息与题设信息之间的联系是什么？根据题设信息已知函数f（x）的定义域，根据选项信息可选择用换元法求f（x）的解析式，这一步骤是可操作的。但是筛选出正确选项的依据是什么？关注到题设信息“函数”，可追问求出来的关系式是“函数的表示形式”吗？这一抽象思维过程是难点。因此此题的思维盲点在于我们想要了解的数学对象是什么，如果能确立数学对象为函数的解析式，结合对函数定义的考量，此题即破。

基于上述三个方面的教学实际需求，本文拟通过研究高中函数模块中解题的教学实践，归纳总结出以确立适切的数学对象是数学问题解构的关键环节，并以案例的形式确立数学对象来解题。

二、实践尝试

（一）基于函数模块的数学对象的分类

1.理论基础

（1）数学的语言功能

数学是具有独特的符号系统和严谨的表达方式的一门语言。数学解题可以看成是运用数学语言进行数学阅读、表达和交流的过程，也是培养学习者学会思考、学会逻辑思考、创造性思考，从而达成认识问题、解决问题的微实践。

（2）数学的核心素养

认识数学问题的观点越高，数学问题越简单、朴素、自然，越透彻。高观点的核心要素就是需要具备良好的知识结构和广泛的知识面，同时能够用最朴素的思想去推动数学问题解决的整个思维过程。在函数模块对运用函数的观点和运动变化的观点进行深度思考，抽象出适切的数学对象，以此数学对象为核心，通过数学运算与直观想象及数据分析探寻数学对象与待求数学问题目标之间的数学联系，进行精准的数学运算和逻辑推理，达成解决问题的目的。

普高数学新课程标准提出学生数学学习的六大核心素养：

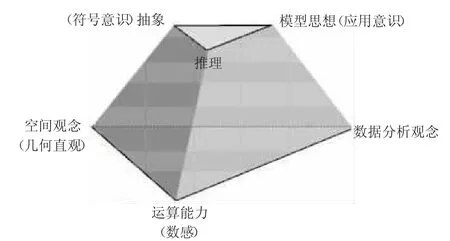
在解决数学问题的过程中可以很好地锻炼学生抽象、建模、数据分析、运算等核心素养，不仅解决了数学问题，还“繁殖”出数学素养的“蘑菇群”。通过多年数学解题策略的研究，本人认为函数模块中可以从题设中提取出问题解决的核心点——数学对象，并以此数学对象为核心探寻与问题目标的本质联系，以这样一种最朴素的思想去思考，让整个解题思维过程自然流畅。

2.分类设计

本文所指函数模块数学解题中的数学对象特指：方程、函数、不等式三类。因为代数问题探究的基本上是等量关系和不等关系，其中等量关系中需要能分析出解决该问题时需要把等量关系看成方程还是函数展开探究，但有时候不考虑所含字母的身份，只是看成等式就可以解决问题。

【案例 3】（2016 浙江 12）

设函数f（x）=x3+3x2+1，已知a≠0，f（x）-f（a）=（x-b）（x-a）2，x∈R，则 a=___；b=___.思路——数学对象：等式x3+3x2-a3-3a2=（x-b）（x-a）2；a≠0；数学对象研究方向：等式的恒等变形；

处理方法：对等式左边进行因式分解与右侧对照，求出a，b的值。

左边=x3+3x2-a3-3a2=（x-a）［x2+（a+3）x+a2+3a］

右边=（x-a）［x2-（a+b）x+ab］

（二）基于数学对象的一题多解案例

有些数学问题很明显能获得这样的信息：只需要把题设中的函数研究清楚就可以解决问题，研究的方向一般为函数的图象和函数的性质两方面，作出函数的图象或者对函数的图象进行适当变换达到问题目标，或者通过研究函数的性质获取与问题目标关联的信息，从而解决问题。但是函数的选择是否适切关系到能否顺利、快速、精准地解决问题。因此下面的案例从三种不同的数学对象选择入手进行剖析，获得一题多解的解题方向。

【案例 4】（2017 浙江 17）

此题主要考查学生的直观想象、数学抽象、数学建模等核心素养，运用观察、类比、化归的策略来解决问题。其中抽象数学对象的思路有三种：函数、方程、不等式。

数学对象研究方向：f（x）的最大值为5；

思路 2.数学对象：函数 g（t）=|t-a|+a，t∈［4，5］；

数学对象研究方向：g（t）的最大值为5；

处理方法：注意到g（t）在t∈R上的图象关于直线t=a对称，且在（-∞，a］上单调递减，在［a，+∞］上单调递增，立得

数学对象研究方向：h（t）的图象变换；

处理方法：把 h（t）的图象向下（a＞0）或向上（a＞0）平移 |a|个单位，然后对x轴下方的图象关于x轴对称翻折，之后再把所得图象向上（a＞0）或向下（a＞0）平移 |a|个单位，使得最高点为纵坐标为5。

数学对象研究方向：确保不等式恒成立且等号能成立；

本文以此案例的解析立足于数学对象的确立，通过对比分析，藉希望读者可以斟酌出对自己最适切的数学对象，以达到“他山之石可以攻玉”的研究价值。

（三）基于数学对象的一题多变案例

平时在数学解题教学中，教师和学生的关注度更多在解题技巧方面，除非对这种技巧运用得非常纯熟，否则应试时易找不准方向。如果在平时教学中就时刻渗透着眼于数学对象的解题方向的探寻，那无论怎样的问题拿到都能如侦探破案一样追寻到解题线索。下例为本人某一节作业分析课时开展的基于数学对象与问题目标之间联系的一题多变的解题教学片段：

【案例5】

已知函数f（x）=x2-（a+2）x+2-a集合A={x∈N|f（x）<0}中只有一个元素，求实数a的取值范围。

思路1.数学对象：函数f（x）=x2-（a+2）x+2-a.

数学对象研究方向：x∈N，f（x）的符号；

处理方法：从变化中挖掘出定值，f（-1）=5（定值），f（0）=2-a，f（1）=1-2a，f（2）=2-3a，f（3）=5-4a，由此展开探究：

（1）若f（0）=2-a<0，则f（1）<0，f（2）<0，f（3）<0，此时集合A中元素不唯一，符合条件；

（2）若f（0）=2-a>0，

②若f（1）<0，由集合A中元素唯一性，则必须满足f（2）≥0，解得

思路 2.数学对象：关于 x 的不等式 x2-（a+2）x+2-a<0，x∈N

数学对象研究方向：不等式只有一个自然数解。

处理方法：参变量分离，数形结合。