桥梁结构系统地震易损性分析方法研究
2018-11-21吴文朋李立峰
吴文朋, 李立峰
(1. 湘潭大学 土木工程与力学学院, 湖南 湘潭 411105; 2. 湖南大学 土木工程学院, 长沙 410082;3. 湘潭大学 工程结构动力学与可靠性分析湖南省高等学校重点实验室, 湖南 湘潭 411105)
既往的桥梁地震易损性研究偏向于基于单一构件的地震易损性分析[1],但桥梁工程是由多种构件组成的复杂系统,任何构件的损伤都可能导致桥梁使用功能的失效。例如,桥台损伤往往不会直接导致桥梁的结构性破坏,但是它可能会阻断桥面上的交通,间接导致桥梁失去通行能力而引起经济损失。因此有必要研究桥梁工程不同构件的地震易损性,为了进行桥梁的概率性地震风险评估,还需建立其系统地震易损性曲线。
桥梁结构在地震作用下的失效概率比任何单一构件的失效概率都要高[2]。不同学者提出了不同的方法进行桥梁系统地震易损性分析。Shinozuka等[3]假定桥梁的系统易损性服从对数正态分布,并采用极大似然法来估计其均值和离差。Mackie等[4]采用有限元可靠度分析方法预测桥梁系统极限状态,建立了桥梁在系统层次的易损性曲线。Choi等[5]同时考虑支座、墩柱两类构件发生地震损伤的相关性,首次采用一阶界限法建立了桥梁系统易损性曲线的上下界限。Pan等[6]在研究美国纽约地区的桥梁地震易损性时,考虑了墩柱和支座两类构件的损伤,但只考虑相关性较大的构件之间的联合失效,采用近似的二阶界限法建立了桥梁的系统易损性曲线。李立峰等[7]考虑了桥墩、支座和桥台三类构件失效模式之间的相关性,采用完整的二阶界限法建立了中等跨径RC连续梁桥的系统易损性曲线。Nielson等首先建立了考虑各种失效模式之间相关性的联合概率地震需求模型(Joint Probabillistic Seismic Demand Model, JPSDM),然后基于Monte-Carlo模拟得到桥梁在不同水准地震作用下的系统失效概率。Zhang等[8]先假定各构件失效对桥梁系统失效的贡献率(墩柱失效权重0.75,支座失效权重0.25),并根据IDA方法计算桥梁的系统失效概率。刘骁骁等[9]综合考虑桥梁不同构件损伤对系统易损性的影响,提出了桥梁体系多维概率地震需求分析方法。Wu等[10]针对中等跨径混凝土斜拉桥体系,提出了基于条件边缘乘积法(Product of the Conditional Marginal, PCM)的快速系统地震易损性分析方法。宋帅等[11]提出了基于多元Copula函数的桥梁体系地震易损性分析方法。
综上所述,各国学者都在试图寻找一种准确建立桥梁系统易损性曲线的方法。然而,一方面,国内目前关于桥梁系统易损性的研究仍主要采用一阶界限法[12],尽管该方法容易为大众所理解、可操作性较强,但一阶界限法得到的系统易损性曲线的上下界限会过宽而失去意义。另一方面,既有的各种系统易损性分析方法在使用上都有一定的局限性,如何更好的选用分析方法有待进一步研究。
本文以一座等墩高多跨钢筋混凝土连续梁桥为例,基于OpenSEES分析平台建立有限元模型,然后输入大量地震波进行非线性时程分析,同时考虑桥墩、支座和桥台等构件的破坏,分别采用多种分析方法建立了桥梁的系统地震易损性曲线。通过这些系统易损性曲线的对比分析,讨论了各种分析方法的适用性和合理性。
1 桥梁系统易损性分析方法
1.1 一阶界限估计法易损性
一阶界限法估计法可以预估结构系统的最大和最小失效概率,以确定失效概率的最大界限区间。各失效模式之间为正相关(ρij≥0)的桥梁串联模型,其一阶界限估计区间可用下式表示
(1)
式中:Psys为结构系统失效概率;Pfi为第i种构件失效的概率;n表示可能失效的构件数目。式(1)中的下界表示所有构件完全正相关(ρij=1),此时只要有一个构件失效,其它构件会迅速相继失效,因此,下界由结构失效概率最大的构件决定;相反,式(1)中的上界表示所有构件完全相互独立(ρij=0),是对系统失效的一种理想保守估计。
1.2 二阶界限估计法易损性
假定桥梁不同构件之间完全相关或完全独立是两种极端情况,会导致一阶界限估计法得到的系统失效概率区间过宽。为解决这个问题,Ditlevsen提出了一种考虑了不同失效模式之间相关性的二阶界限估计法
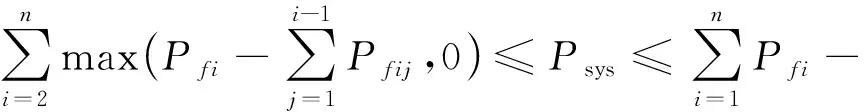
(2)
式中:Pf1为单个构件失效的概率;Pfi为第i个构件失效的概率(Pf1除外);Pfij表示第i个和第j个构件同时失效的概率,可用下式表示
Pfij=Pr(Fi∩Fj)
(3)
式中:Fi和Fj为第i和j个失效事件。式(3)涉及到二维联合失效概率的计算,其算法在相关文献[13]中有详细说明,本文不再赘述。此外,需要特别指出的是,式(2)中构件失效模式的排列顺序对边界宽度的估计有较大影响。一般情况下,决定其上界最小值的失效模式排列顺序与决定其下界最大值的失效模式排列顺序并不一致。因此,要想得到最优二阶界限法易损性曲线,要经过n次的计算,既往的研究表明,按Pf1≥Pf2≥Pf3≥…≥Pfn的顺序进行排列时可获得相对较窄的失效区间。
1.3 基于Monte-Carlo模拟的系统易损性
Nielson等基于Monte-Carlo模拟提出了一种更为直接的系统易损性分析方法。首先建立不同构件的概率地震需求模型(Probabilistic Seismic Demand Model, PSDM),然后考虑不同失效模式间的相关性,建立联合概率地震需求模型。假定不同构件的地震需求服从对数正态分布,如果用随机向量X=(X1,X2,X3,…,Xn)来表示n个构件的地震需求,则X的边缘分布都服从对数正态分布。对X中的每个元素进行对数转换Yi=ln(Xi),则随机向量Y=(Y1,Y2,Y3,…,Yn)服从正态分布。如果假定联合概率分布也服从正态分布,则此时只需确定均值向量μY和相应的相关系数矩阵ρij[n×n],即可建立多构件的JPSDM。需要说明的是,JPSDM中的相关系数矩阵并非直接来源于不同构件响应值之间的相关系数,而是用各构件响应对数值之间的相关系数来代替
(4)

(5)
式中:[X1,X2,…,Xn]为由随机抽样得到的n个构件需求值组成的向量;[Sc1,Sc2,…,Scn]为由随机抽样得到的n个构件在第i个损伤状态的能力值组成的向量;DSi为第i个损伤状态。由式(5)可知,当所有构件的地震需求均小于其抗震能力时,指标函数等于0,否则就等于1。根据指标函数进行统计分析,可计算不同损伤状态下桥梁结构的系统失效概率
(6)
式中:N为抽样次数;对于指定的第i种损伤极限状态(DSi),在不同的地震动强度(Intensity Measure, IM)时进行抽样和统计分析,即可得到不同IM处的桥梁系统失效概率点,最后采用对数正态分布函数对这些数据点进行拟合,则可得到相应的系统地震易损性曲线。需要指出的是,在对不同构件的抗震能力进行抽样时,每次抽样过程中,相同构件在不同损伤状态的样本应该满足
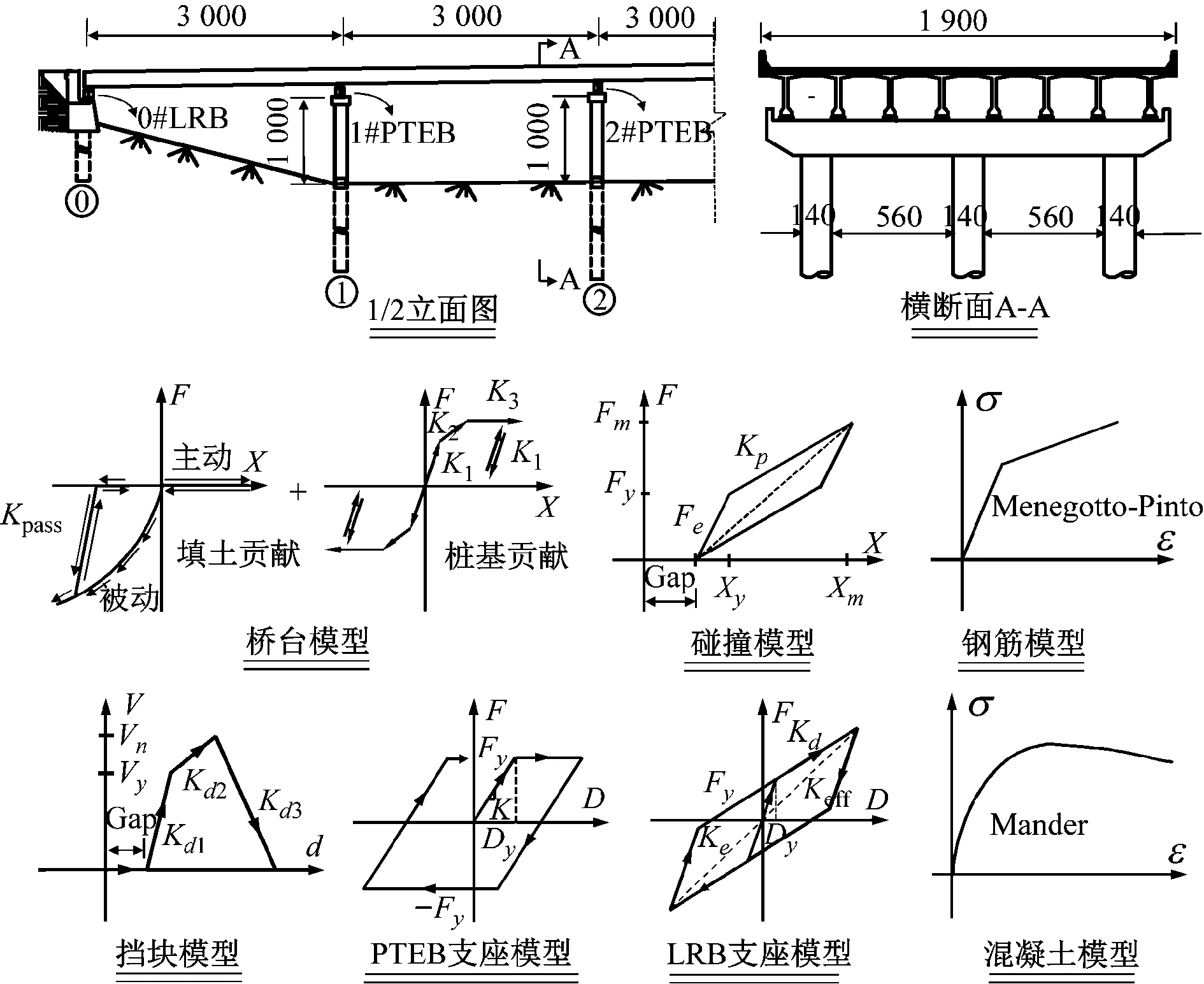
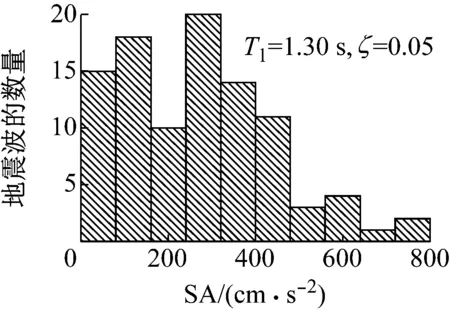
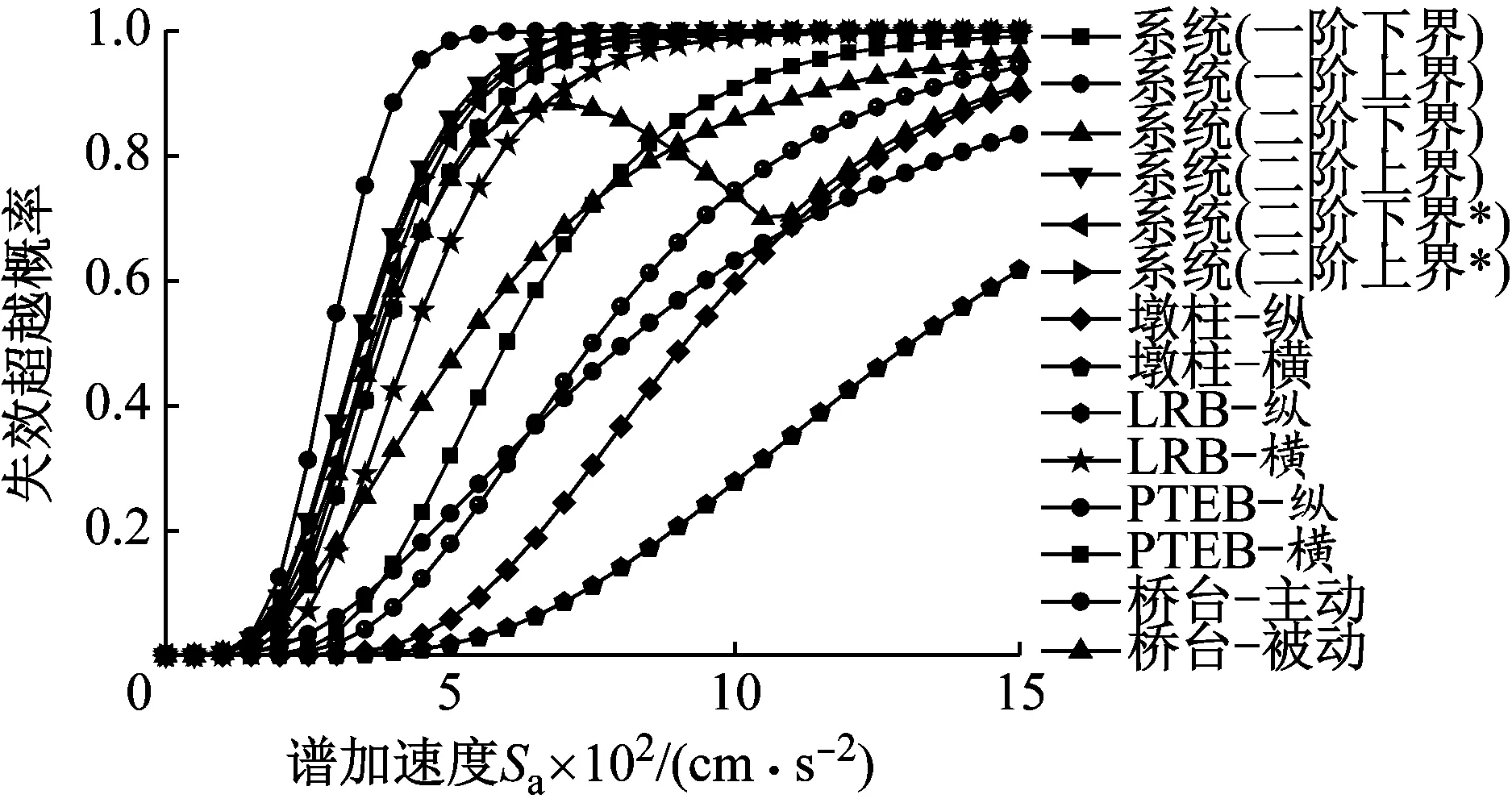
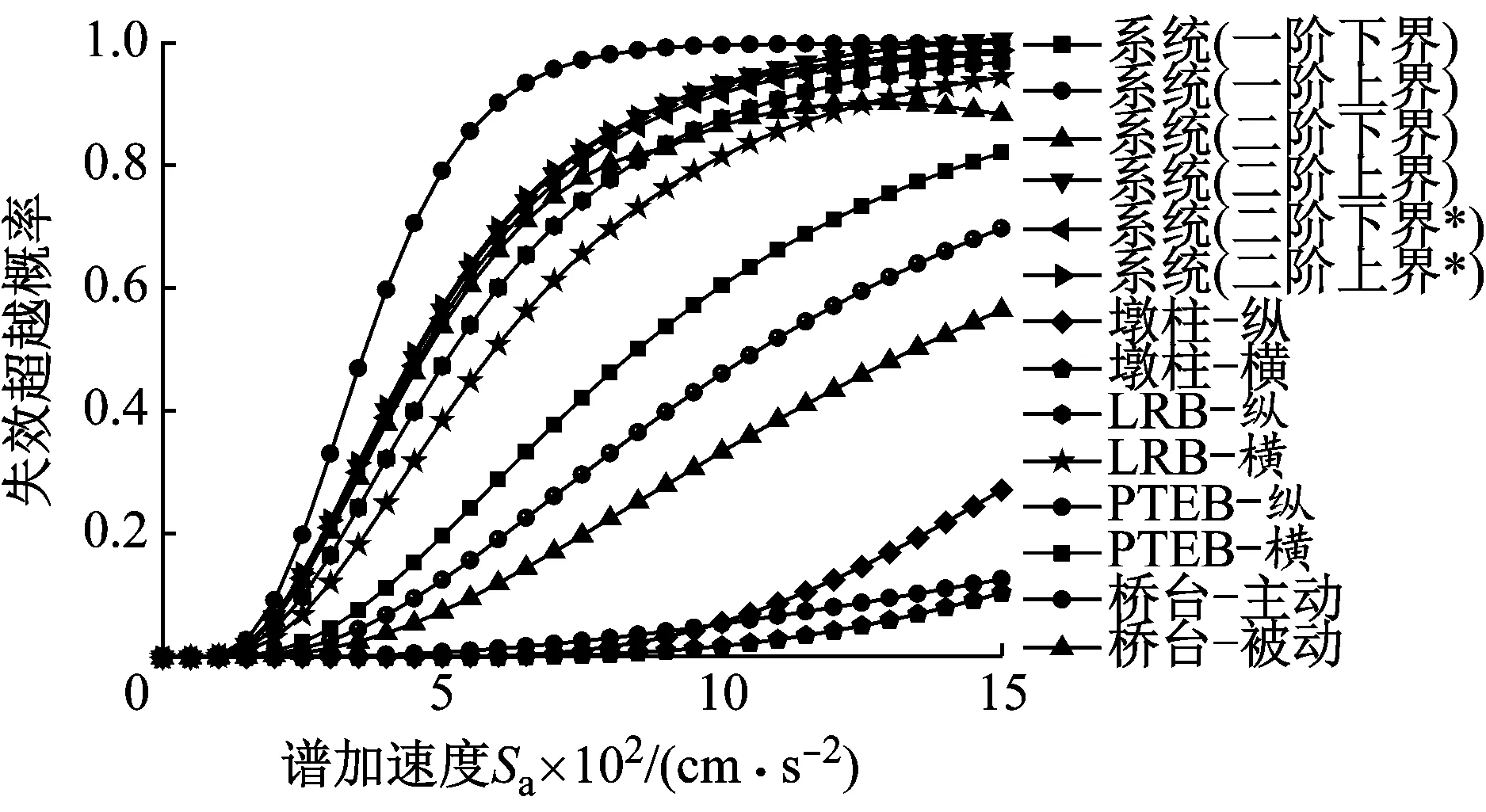
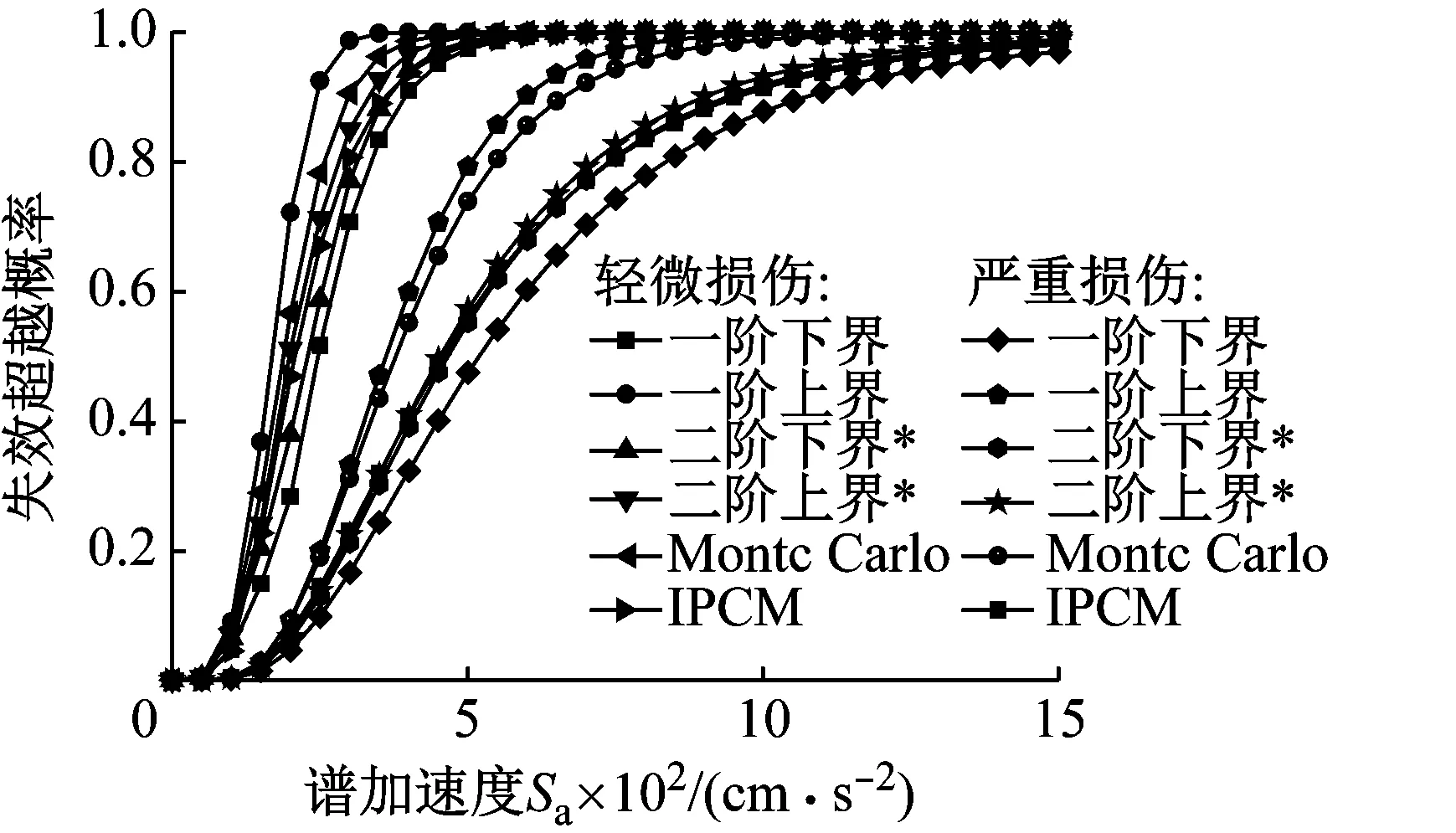
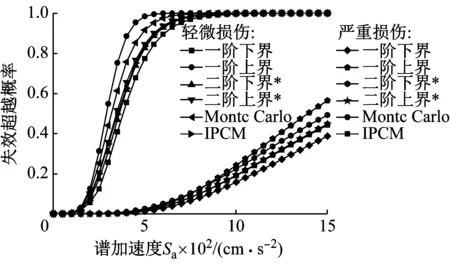
Sc(DS1) (7) 式中:DS1,DS2,DS3和DS4分别为轻微损伤、中等损伤、严重损伤和完全破坏四种极限状态。实际操作中,式(7)可以通过假定同一构件的四种损伤状态完全相关来保证。 多维标准正态累计分布函数Φn(β,ρ)的近似求解方法是解决复杂结构系统可靠度问题的一种有效分析方法。条件边缘乘积法(PCM)以其简单高效的优点而非常适合于实际工程的应用。PCM法根据条件概率理论,将多维联合分布函数写成一系列条件概率相乘的形式,而每个条件概率都可以被近似成一维的标准正态分布函数。此时多维标准正态分布函数可表示成Markov链的形式 (8) 式中:Φn(·)为n维标准正态分布函数;n为失效模式的个数;β=[β1,β2,β3,…,βn]为n个构件的可靠度指标向量;ρ=[ρij]n×n为相关系数矩阵;βk|(k-1)为条件正态分位数 (9) 式中:Φ-1(·)为标准正态分布函数Φ(·)的逆;根据Pandey[14]的公式推导,可得条件正态分位数的计算公式如下 (10) 式中:k=1,…,n-1;i=k+1,…,n,条件参数Ak|(k-1)和Bk|(k-1)分别用下式计算 Ak|(k-1)=φ(βk|(k-1))/Φ(βk|(k-1)) (11) Bk|(k-1)=Ak|(k-1)(βk|(k-1)+Ak|(k-1)) (12) 式中:φ(·)为标准正态概率密度函数。式(10)中的条件相关系数ρik|(k-1)可用下式计算 ρ(i+1)(k+1)|k= (13) 根据以上公式推导,很容易编写相关的循环计算程序来计算结构的体系失效概率。Wu等以上述方法为基础提出了基于PCM法的桥梁系统地震易损性分析方法,并给出了详细的分析流程。 算例桥梁为一座4×30 m的连续梁桥,上部结构由8片T梁组成,桥面宽19 m,材料为C40;中间桥墩是由3个直径1.4 m的圆柱和盖梁组成的排架式桥墩,墩高均为10 m,材料为C30;桥墩截面沿环向布置30根纵筋,配筋率1.6%;采用螺旋式箍筋,体积配箍率0.6%,纵筋和箍筋的材料均为HRB335。桥墩盖梁处设置8个型号为GJZ 450×450×114的板式橡胶支座;两岸桥台采用桩基支承的座式桥台;桥台处采用铅芯橡胶支座;桥墩盖梁和桥台处在横桥向均采用滑移混凝土型挡[15]。 基于OpenSEES源代码分析平台[16]建立桥梁有限元模型。主梁采用弹性梁单元模拟;墩柱采用弹塑性纤维梁单元模拟,其中混凝土和钢筋的应力-应变关系分别采用Concrete 04 和Steel 02材料,模型参数来自Mander模型和Menegotto-Pinto模型;支座均采用Elastomeric Bearing Element模拟;桥台模拟考虑了台后填土和桩基的双重贡献,采用Hyperbolic Gap Material和Hysteretic Material并联模拟;挡块采用徐略勤等提出的滑移型挡块力学模型进行模拟;桥台处的碰撞采Impact Material进行模拟。本文不考虑桥墩处桩-土相互作用的影响。以上各个构件的力学模型如图1所示。 图1 算例桥梁有限元模型(单位:cm)Fig.1 Finite element model of the bridge (unit: cm) 本文选取了100条远场实测地震波进行输入,由于选取远场地震波的强度较低,为更多地激励起桥梁的非线性响应,将所有地震波的峰值地面加速度(PGA)放大2倍。考虑地震动强度参数(IM)的效率性、实用性和充分性时,PGA并不是理想的IM,而谱加速度(SA)更适合做规则桥梁地震易损性分析的IM,因此本文以算例桥梁基本弹性周期(T1=1.3 s)对应的SA作为地震易损性分析的IM。缩放后的100条地震波的SA分布情况如图2所示。 图2 输入地震波谱加速度的分布情况Fig.2 Distribution of the spectra for 100 records 桥梁工程主要由上部结构、下部结构和支座等构件组成,每个构件都对结构的完整性发挥着重要作用。与建筑结构相比,桥梁结构更加强调使用功能的完整性。例如,桥梁伸缩缝发生了地震破坏,会导致两岸路面上的车辆无法正常驶入桥面,即使此时的主梁和桥墩等桥梁主体构件的剩余承载能力足以保障人员和车辆顺利通行,但桥梁使用功能的完全性已经遭到破坏。从结构力学的角度看,尽管桥梁的整体力学特性仍然健全,具有一定承载能力。然而,桥梁已失去了正常通行能力,在地震易损性分析中仍把这种状态定义为桥梁损伤。因此,本文所指的桥梁或构件失效并不是结构力学意义上的结构破坏,而更多的强调地震对桥梁整体使用功能的破坏。 如果假定桥梁由不同的构件串联组成,则可以采用串联模型来计算其在地震作用下的系统失效概率,既往的桥梁系统地震易损性分析多是基于串联模型。串联模型中任何构件发生某种程度的损伤都意味着结构整体发生相同损伤等级的损伤。因此模型中每个构件的重要性都完全相同。但也有学者提出在采用串联模型时应按不同的权重来考虑桥墩和支座对桥梁系统易损性的贡献。可见,地震作用下的桥梁系统可靠度模型该如何确定,还没有统一的定论。 本文根据既往桥梁震害的实际情况,假定在不同的损伤状态采用不同的串联模型,以此区分各构件对系统易损性的贡献。本文同时考虑了桥墩、铅芯橡胶支座、板式橡胶支座和桥台四类构件的地震破坏。显然,桥墩肯定属于重要构件之一,因此认为桥墩对桥梁系统的四种损伤状态都有重要影响。中间桥墩处的PTEB,即使发生完全破坏,一般也不会导致落梁破坏。因此本文只考虑PTEB对桥梁系统前三种损伤状态的影响;对于桥梁两岸桥台处的LRB,其损伤程度过大则可能导致上部结构发生落梁破坏,因此在四种损伤状态下都得考虑。本文采用了带背墙和翼墙的座式桥台,在强地震作用下背墙被设计为“牺牲”构件,以保护桥台对桥梁整体的支撑功能,因此不考虑桥台对系统完全破坏的影响。本文多跨混凝土连续桥梁采用的系统可靠度模型如下 (14) 式中:∞为各构件组成串联模型;SL为轻微损伤;MO为中等损伤;EX为严重损伤;CO为完全破坏。可见本文在完全破坏状态只考虑了桥墩和桥台LRB的贡献。需要指出的是,尽管该系统可靠度模型能避免将所有构件的重要性完全等同带来的误差,但这种处理方式仍具有一定的主观性。 损伤指标是用来衡量结构或构件破坏状态的限值,该指标与易损性分析中的工程需求参数相关。美国FEMA灾害损失风险评估软件HAZUS-MH-MR5[17]中对桥梁的轻微损伤(SL)、中等损伤(MO)、严重损伤(EX)和完全破坏(CO)四种损伤等级进行了详细的描述,本文基于HAZUS-MH-MR5定义算例桥梁的损伤指标。假定构件损伤指标服从对数正态分布,则各构件在不同损伤状态的抗震能力可用中值Sc和对数标准差βc表示。在没有足够试验数据信息来评估损伤状态对数标准差时,从主观上假定不同损伤状态的βc对易损性分析是合理的。本文主要考虑桥墩、铅芯橡胶支座、板式橡胶支座和桥台(主动+被动)的损伤,根据既往的研究,其损伤指标分别采用曲率延性比(μφ)、支座剪切应变(γ)、位移延性比(μΔ)和桥台相对变形(δacti,δpass)来表示,各个构件的损伤指标如表1所示。 表1 不同构件的损伤指标Tab.1 Damage states of different components 需要指出的是,尽管橡胶的破坏剪切应变可达400%~500%,但桥梁工程中一般假定γ=250%时即会发生完全破坏。表1中铅芯橡胶支座在完全破坏状态的极限(525%)也并非真实的橡胶剪切应变,而是先根据可能发生的落梁情况来确定支座的相对位移,再换算成支座的剪切应变。 地震易损性曲线表示结构在地震作用下的地震需求达到或超过指定损伤极限状态的失效概率,地震易损性函数一般可表示为 (15) (16) (17) 式中:a,b为估计参数;Di为结构在第i条地震波作用下地震响应峰值;N为非线性动力分析的次数。 根据式(15)~式(17)可以得到算例桥梁不同构件的构件易损性曲线,然后基于前文中假定的桥梁系统可靠度模型,运用不同的系统易损性分析方法得到桥梁结构的系统地震易损性曲线。 图3为轻微损伤和严重损伤两种状态下的构件易损性曲线和界限估计法系统易损性曲线的对比情况。由图可知,桥梁系统失效的概率要高于任何单个构件的失效概率,这表明当桥梁面临多种可能的失效模式时,用单个构件的易损性来代表结构整体的易损性是不适合的。此外,二阶界限法得到的桥梁系统易损性曲线的失效概率区间要明显小于一阶界限法。图中带“*”号的二阶界限法易损性曲线表示各构件按失效概率“从大到小”的顺序排列的情况,不带“*”号的表示 (a) 中等损伤 (b) 严重损伤图3 系统易损性与构件易损性的比较Fig.3 Comparison of system and component fragilities “随机排列”的情况。由图可知,基于二阶界限法的易损性曲线的下界对构件排列顺序较为敏感,特别是在地震动强度水平较大时,甚至出现了比一阶界限法的下界还小的情况。因此,当各构件按失效概率“从大到小”的顺序进行排列时,得到桥梁系统易损性曲线稳定性较好。 图4为四种不同损伤状态下,由前文中提到的各种系统易损性分析方法得到的桥梁系统易损性曲线的对比情况,其中,二阶界限法仅给出了“顺序排列”的稳定情况。由图可知,基于二阶界限法和PCM法的系统易损性曲线更靠近一阶界限法的下界,且基于PCM法的系统易损性曲线正好位于基于二阶界限法的系统易损性区间内,这表明基于PCM法建立的桥梁系统易损性曲线是准确的。然而,由Monte-Carlo模拟方法得到的桥梁系统失效概率要大于PCM法得到的系统失效概率,甚至比二阶界限区间的上界还要高,而且该曲线更加靠近一阶界限法的上界。 以上分析结果表明,不同分析方法得到的桥梁系统易损性曲线存在一定的差别,特别是基于Monte-Carlo模拟的系统易损性曲线与其它方法的差别较大。实际上,这种由分析方法带来的差别在既往桥梁系统易损性相关研究中也有所体现,例如,Pan等和Wu等采用二阶界限法和PCM法进行的系统易损性分析结果对比;Nielson等和钟剑等[18]在采用Monte-Carlo方法进行的系统易损性分析结果对比。然而,需要指出的是,以上研究并没有指出导致这些差异的根本原因,因此,本文将在下一节对此展开详细的讨论和分析。 (a) (b)图4 不同系统易损性分析方法的比较Fig.4 Comparison of different system fragility analysis methods 前文中提到,一阶界限法给出了桥梁系统失效概率的最大界限区间,结构真实的系统失效概率应根据构件之间相关程度的不同而在此区间内移动。理论上讲,对于同一损伤状态而言,构件之间的相关程度越高,则系统易损性曲线将越靠近一阶界限法的下界,而构件之间的相关程度越低,则系统易损性曲线将越靠近一阶界限法的上界。由于桥梁地震易损性分析各个构件之间的相关系数往往较大,因此从这个意义上来讲,二阶界限法和PCM法得到的系统易损性曲线要更加准确一些。 实际上,界限估计方法和PCM方法得到的系统易损性曲线都直接来源于构件易损性曲线,因此,对于各种不确定性的考虑,只能反映在建立构件易损性曲线的过程中。然而,Monte-Carlo模拟方法得到的系统易损性曲线直接来源于JPSDM以及各构件抗震能力模型,对于各种不确定性因素的考虑则直接体现在Monte-Carlo模拟的随机抽样过程中。可见,基于Monte-Carlo模拟的易损性分析方法不仅能考虑需求的不确定性,还能完整地考虑各构件抗震能力或损伤极限的不确定性。然而,构件易损性分析中主要考虑了地震需求的不确定性,对构件抗震能力不确定性的考虑则通过假定对数标准差βc来体现。 (a) 中等损伤 (b) 严重损伤图5 不确定性对系统易损性曲线的影响Fig.5 Influence of uncertainty on system fragility curves 图5为基于Monte-Carlo模拟但考虑不确定性的方法不同时得到的系统易损性曲线,以及与PCM法系统易损性曲线的对比(以中等损伤和严重损伤为例)。图中,UD表示只考虑地震需求的不确定性;UD+UC表示同时考虑地震需求和抗震能力的不确定性;UD+βC表示同时考虑地震需求的不确定性和以βC表示的抗震能力的不确定性(与构件易损性分析方法相同)。由图可知,如果在Monte-Carlo模拟中只考地震需求的不确定性,系统易损性曲线会更陡,这表明桥梁系统失效的概率随地震动强度的增加而增加得更快;如果在Monte-Carlo模拟中以随机抽样的方式来考虑结构抗震能力的不确定性,即同时考虑了各损伤极限状态均值不确定性的影响,这时的桥梁系统易损性明显会增加;如果在Monte-Carlo模拟中考虑不确定性方法与构件易损性分析方法相同时,则其得到的桥梁系统易损性曲线与PCM是完全重合的。由此可见,正是由于Monte-Carlo模拟方法对抗震能力(损伤指标)不确定性的考虑更为全面,从而导致了得到的桥梁系统失效概率要高于另外两种方法得到系统失效概率。 此外,由前面的分析和讨论可知,Monte-Carlo模拟方法可以不依赖构件易损性分析的结果,在考虑抗震能力不确定性方面有优势。而其它方法不能考虑构件抗震能力均值的不确定性,会低估结构系统的失效概率。然而,一方面结构抗震能力不确定性的量化仍比较困难,目前的研究中大多是基于某种假定,而这些假定是否合理仍有待验证。另一方面尽管Monte- Carlo模拟能更全面地考虑不确定性的影响,但当失效模式过多时会导致计算量偏大。相比而言,PCM方法提供了一种能快速和准确计算桥梁系统可靠度的新途径。因此,对于失效模式较多的复杂体系桥梁,利用基于PCM的系统地震易损性分析方法来建立桥梁系统易损性曲线更为适用。 (1) 界限估计法和PCM法在建立桥梁系统地震易损性时,都直接依赖于前期建立的构件易损性函数,无法独立考虑各类不确定性的影响;Monte-Carlo模拟方法能直接利用JPSDM建立系统易损性函数,在考虑桥梁抗震能力的不确定性方面有优势。 (2) 界限估计法得到的系统易损性曲线仅为一区间形式,而PCM法能快速地建立桥梁结构精确的系统易损性曲线,适合于需要考虑多种失效模式的复杂结构的系统易损性分析。 (3) 本文的研究都是基于同一个假定,即桥梁是一个由不同构件组成的串联系统。然而,实际桥梁结构在地震作用下的破坏并不一定表现出串联效应。因此,能否采用串-并联系统或者自适应系统来研究桥梁的系统易损性仍有待进一步研究。1.4 基于PCM算法的系统易损性
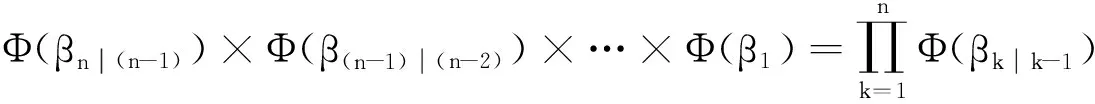
2 桥梁建模和地震动输入
2.1 桥梁建模
2.2 地震波输入
3 桥梁系统地震易损性曲线
3.1 系统可靠度模型假定
3.2 损伤指标
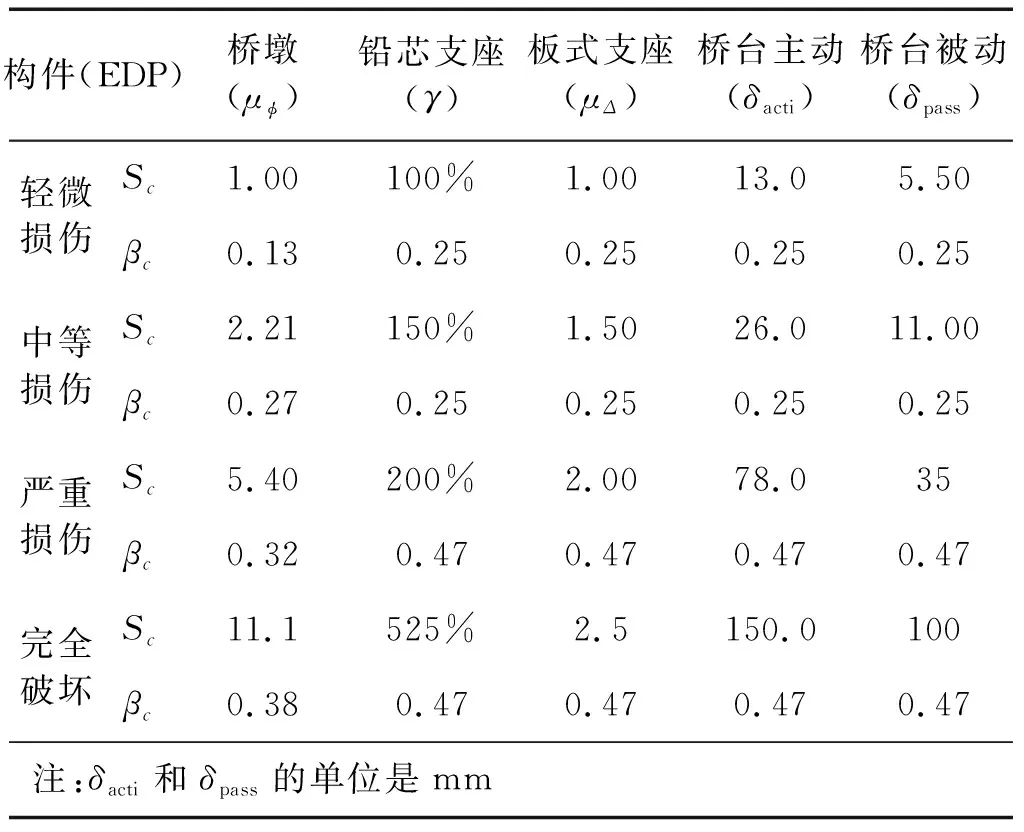
3.3 桥梁系统易损性曲线


4 关于各种分析方法的讨论


5 结 论
