存储式光纤陀螺测斜探管研制

周 策， 刘一民， 罗光强， 孟照魁 ， 焦焕静， 高 爽

(1.中国地质科学院探矿工艺研究所，四川 成都 611734； 2.北京航空航天大学光电技术研究所，北京 100191)

0 引言

钻孔测量技术是地质勘查关键技术之一，在我国地质调查和国民经济其他领域有着广泛的应用前景。为实现国家新能源开发的战略目标，针对超高温大深度钻井温度及定位轨迹探测为目标，研制了一套适用于超高温地层的防磁干扰钻孔轨迹温度测量装置，实现0～270 ℃高温、120 MPa压力环境条件下钻孔各孔深井段倾角、方位角、工具面向角及温度的测量。

超高温钻孔轨迹测量仪(以下简称为测量仪)通过测量各测点空间位置数据，再通过适当的计算方法间接求得各测点的井斜角值、方位角值、钻孔温度值以及孔深值，从而获得井身轨迹数据。可有效提高钻井施工质量，保证施工安全进行。

其主要研究内容包括三维光纤陀螺、三维石英挠性加速度计、光纤陀螺误差分析、光纤陀螺惯测组合井下环境适应性研究、仪器外场标定技术研究等。

1 光纤陀螺测斜探管基本组成

主要由光纤陀螺组件、存储式测控系统和电源组件构成。测量仪系统图如图1所示。光纤陀螺组件主要完成倾角、方位角和工具面角的测量；工作状态下，光纤陀螺组件测得的姿态参数通过串口发送给测控系统，同时组合测得的钻孔温度参数一并存储于存储器中，结束后，传给地面上计算机软件，实现钻孔轨迹分析；电源组件向光纤陀螺组件、存储式测控系统提供耐高温、低纹波、低功耗的直流电源电压。

图1 测量仪系统图

井下部分与地面部分使用钢丝绳连接，进行仪器的投放与提升，测斜探管为存储式，工作时测量的数据就存储在探管内的存储器中。测量完毕，将井下仪器提出钻孔后，取出测斜探管，将测斜探管通过数据线与计算机连接，由计算机中的测量软件读出探管中存储的数据，并进行相应的处理和显示，从而得到测量结果。

2 测量基本原理

光纤陀螺测斜组件是测量系统的核心测试模块，钻孔轨迹测量基本原理是根据牛顿提出的相对惯性空间的力学定律，利用陀螺、加速度计敏感仪器沿钻孔轨迹运动过程中的角速度、加速度，通过实时测量解算计算机进行航位推算计算,得到钻孔井眼各测量点的倾斜角、方位角等参数,用以描述钻孔轨迹。

惯性测量单元(Inertial Measurement Unit，IMU)的核心构成为三轴光纤陀螺、三轴加速度计、导航解算电路以及导航算法，如图2所示。

图2 三轴陀螺惯性测量单元组成

根据三轴加速度计(GX、GY、GZ为X、Y、Z轴方向加速度)输出值，可以建立顶角θ与加速度输出值的关系方程如下：

(1)

本文中捷联惯性导航技术的姿态测量涉及到多种坐标系，分别是惯性坐标系、载体坐标系、地理坐标系和导航坐标系，分别定义如下：

(1)惯性坐标系，简称i系。该坐标系也称作地球固定坐标系，三个坐标轴指向惯性空间固定不动，坐标系原点是地球的重心，Z轴设定为地球自转轴，北向为正，X轴和Y轴设定在赤道面上，且定义X轴指向春分点，Y轴与X轴、Z轴形成右手坐标系。此坐标系是惯性仪表测量的参考标准，是相对惯性空间无任何运动的一个理想坐标系。

(2)导航坐标系，简称n系。导航坐标系是捷联惯性导航系统在求解导航参数时使用的坐标系，本文中导航坐标系为地理坐标系。

(3)地理坐标系，简称g系。对于北东地坐标系的定义为：原点O为载体的重心，X轴指向北，Y轴指向东，Z轴沿垂线指地。

(4)载体坐标系，简称b系。载体坐标系相对于地理坐标系所确定，其状态用姿态角来表示。坐标系构成右手直角坐标系，原点O为载体的质心，X轴指向载体纵轴，Y轴指向载体横轴，Z轴沿垂线指地。

如图3所示，欧拉角的动态定义把欧拉角看成3次连续转动而形成的。由上述4个坐标系的定义可知，载体平台的姿态角度由方位角α，顶角θ和工具面角β所确定，这3个被测角即是导航坐标系(地理坐标系)与载体坐标系之间的欧拉变换角度。如图4所示，导航坐标系(地理坐标系)XYZ绕Z轴旋转α角，得到X′Y′Z坐标系；再绕Y′轴转θ角，得X′Y′Z′坐标系；绕X轴转β角，则得到载体坐标系X″Y″Z′。

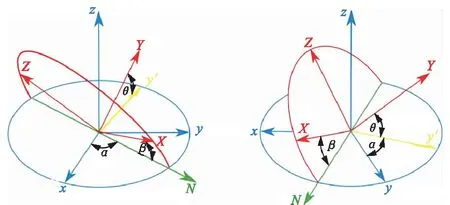
图3 欧拉角的动态定义

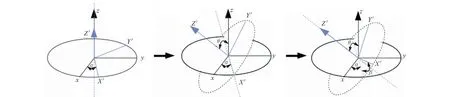
图4 导航坐标系与载体坐标系的欧拉变化

由上述分析可以推导出导航坐标系和载体坐标系之间的转换矩阵为:

(2)

由此,将式(2)展开可得：

(3)

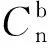
(4)

(5)

其中：

式中Λ是从载体系到导航系的转动四元数，它通过旋转轴和绕该轴旋转的角度构造，有式(6)，方位角α，顶角θ，工具面角β的计算：

(6)

式中：α——绕旋转轴旋转的角度；cosβX、cosβY、cosβZ——分别为旋转轴在X、Y、Z方向的分量。

(7)

三轴陀螺的井眼轨迹姿态位置测量原理如图5所示。

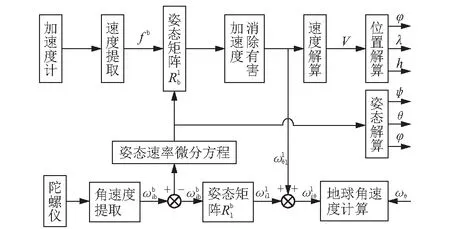
图5 三轴陀螺的井眼轨迹姿态位置测量原理框图

3 三维干涉型光纤陀螺

测斜仪采用三维干涉型光纤陀螺仪，干涉式光纤陀螺通过采用多匝光纤线圈来增强相对线性空间的旋转引起的萨格奈克效应。干涉式光纤陀螺的主体是一个Sagnac干涉仪，由光源、光纤耦合器、光探测器、Y分支多功能集成光学芯片和光纤环组成，测量原理如图6所示。

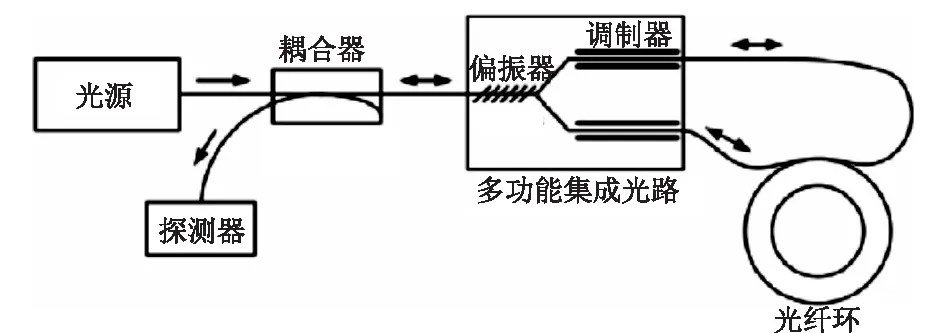
图6 干涉式光纤陀螺结构组成

(1)光源:激光作为陀螺的光源，提供了一束稳定、连续的相干光来引起Sagnac效应。超辐射发光二极管(SLD)由于体积小、输出功率适中、光谱较宽等优点，广泛应用于低精度光纤陀螺中。高精度光纤陀螺则主要采用1.55 μm宽带超荧光掺铒光纤光源。

(2)耦合器:耦合器提供了发送由光纤环至探测器的返回光的基本功能，同时允许光束从光源传递到光纤环。

(3)多功能集成光学芯片:光纤陀螺无源器件集成化最典型的是Y分支的LiNbo3集成光学芯片，它集成了一个偏振器、一个分束器和两个宽带相位调制器的功能。

(4)探测器:光纤陀螺所采用的光电探测器是半导体PIN光电二极管，它的作用是把接受到的光电信号转换成相应的电信号。目前所使用的光电探测器是由PIN场效应管FET单片集成制成的PIN-FET光接收机前置放大器组件。

(5)光纤环:光纤环是光纤陀螺的核心部件，具有足够的长度并以小体积的多匝光纤线圈形式出现。通常将一定长度的光纤缠绕在圆柱形骨架上构成光纤环。当光纤环绕中心轴旋转时，线圈中两束相向传输的光会产生一个相位差，即Sagnac相移，通过对相位差的检测，即可得到被测角速度。

4 三维石英挠性加速度计

采用三维石英挠性加速度计，图7为石英挠性加速度计的内部结构图，在石英挠性加速度计工作时，沿运动方向的重力场分量将推动敏感元件运动。当石英敏感元件在失去平衡的状态下会有电信号输出，输出信号经过伺服电路放大后使力矩器线圈中通过一定比例的电流，载流线圈在力矩器磁场的作用下产生一个反力，该力将推动敏感元件复位。当重力加速度的分量越大，产生的反力和伺服电流就越大；若重力加速度的分量反向，产生的反力和伺服电流也会反向。该电信号与重力加速度在该轴上的分量成正比，可以从精密电阻(已知电阻值)上产生的压降求得。

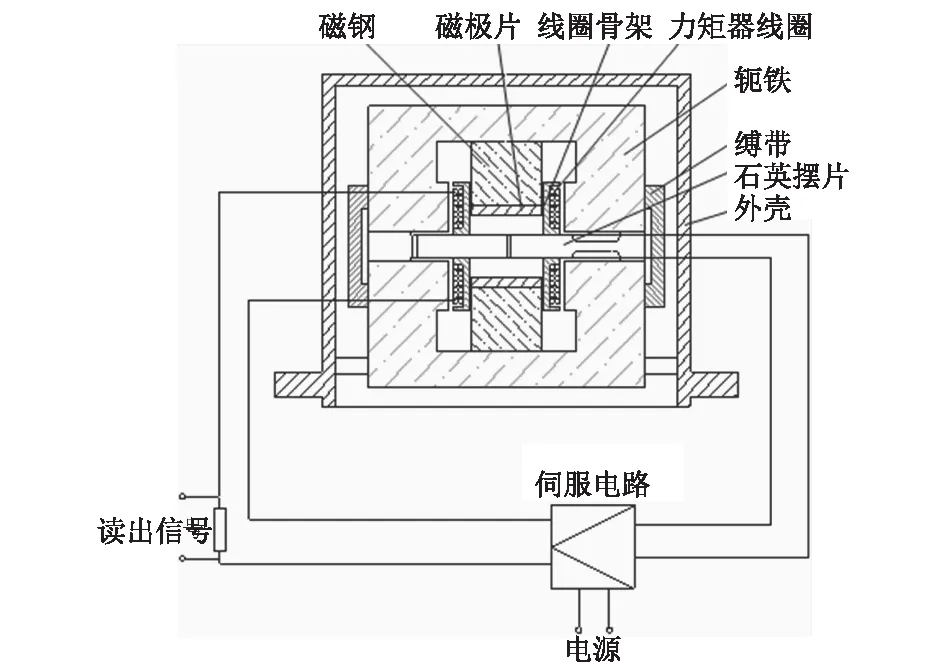
图7 石英挠性加速度计的内部结构图

5 光纤陀螺误差分析

光纤陀螺是光纤惯性组合测斜系统的核心测量传感器，其误差是决定测斜系统测量精度的主要误差源。光纤陀螺误差可以分为确定性误差和随机误差两部分，其中确定性误差可以通过精确标定加以补偿，随机误差则成为影响光纤陀螺测斜系统长时间工作精度的主要误差源。为确保光纤陀螺测斜系统精度，必须分析和辨识光纤陀螺的随机误差特性，并建立定制的随机误差模型，以便采取有效措施对随机误差进行补偿。首先利用功率谱密度和Allan方差法分析和辨识出光纤陀螺随机误差中的主要误差成分，在此基础上，利用时间序列分析法建立定制的光纤陀螺随机误差模型，从而为随机误差的补偿和组合滤波器的设计奠定基础。

5.1 功率谱密度法

功率谱密度(Power Spectra Density，PSD)是最为常用的随机信号分析和辨识方法。

功率谱密度的求取是以信号的自相关函数为基础的，光纤陀螺随机误差的自相关函数定义为：

R(τ)=E[x(t+τ)x(t)]

(8)

式中：x(t)(t=1,2,…,N)——随机误差序列；τ——相关时间。

自相关函数反映了在时域内不同时间点光纤陀螺随机误差的相互关系。随机误差频域内的特征可由其功率谱密度表示，双边功率谱密度定义为其自相关函数的傅立叶变换：

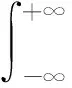
(9)

在分析光纤陀螺随机误差时，对其单边功率谱密度进行分析，定义如下：

S(ω)=(1/T)|X(ω)|2

(10)

式(10)中，X(ω)表示X(t)的傅立叶变换，在计算时常用X(t)在频率点fj的离散傅立叶变换X(f)来近似X(ω)，其中：

(11)

光纤陀螺随机误差的单边功率谱密度可由下式近似求得：

(12)

实际应用中功率谱密度法存在一些不足。首先是各误差的功率谱密度曲线并非各自不同，一些不同的误差具有相似的双对数曲线，而且对于一些需要重点辨识的误差，其双对数曲线也有相似现象，因此利用功率谱密度法可辨识的误差种类较少。此外，功率谱密度法只给出随机误差的功率谱密度函数在频域上的曲线，而不能直接给出各误差的时域特性，因此还需要对辨识结果做进一步处理。

5.2 Allan方差法

(13)

则Allan方差定义为：

(14)

式中：τM=Mt0——组相关时间。

Allan方差是基于有限长度数据的估计，其可信度依赖于独立的组数。估计的百分比误差与独立的数据组数的关系为：

(15)

式中：e——百分比误差；K=N/M——独立的数据组数。当选取的独立的数据组数越多，其估计越准确，所以在参数辨识时应有目的的将组数选得较大,以免出现辨识误差。

Allan方差与原始数据中噪声的功率谱密度有关，其与功率谱S(f)间的关系由式(15)给出，它是Allan方差的频域表达式。

(16)

由以上可以看出，滤波器的带通取决于τ，不同类型随机过程的辨识可以通过调节滤波器的带通来检验(即用不同的τ来检验)。因此，Allan方差可以辨识并量化数据中存在的不同噪声项，通常用σ-τ的双对数曲线来表示。

5.3 误差的主要分量

光纤陀螺随机误差的主要分量通常包括量化噪声、角度随机游走、速率随机游走、偏置不稳定性和速率斜坡等。

根据功率谱密度和Allan方差的基本原理和计算方法，计算并绘制光纤陀螺随机误差的功率谱密度曲线和Allan标准差曲线，如图8所示，定性分析光纤陀螺的随机误差特性。从功率谱密度曲线中可以看出，光纤陀螺具有较大的高频噪声，而低频部分则主要表现为速率随机游走。同样从Allan标准差曲线中可以看出，当相关时间较短时，以量化噪声和角速度随机游走为主，而相关时间较长时则表现出速率随机游走特性。

利用最小二乘法拟合Allan标准差曲线辨识出各项随机误差分量，如表1所示。

表1 光纤陀螺随机误差信号Allan方差辨识结果

注：Q-量化系数；N-角度随机游定系数；B-零偏不稳定性系数；K-角速率随机游走系数；R-速率斜坡系数。

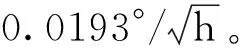
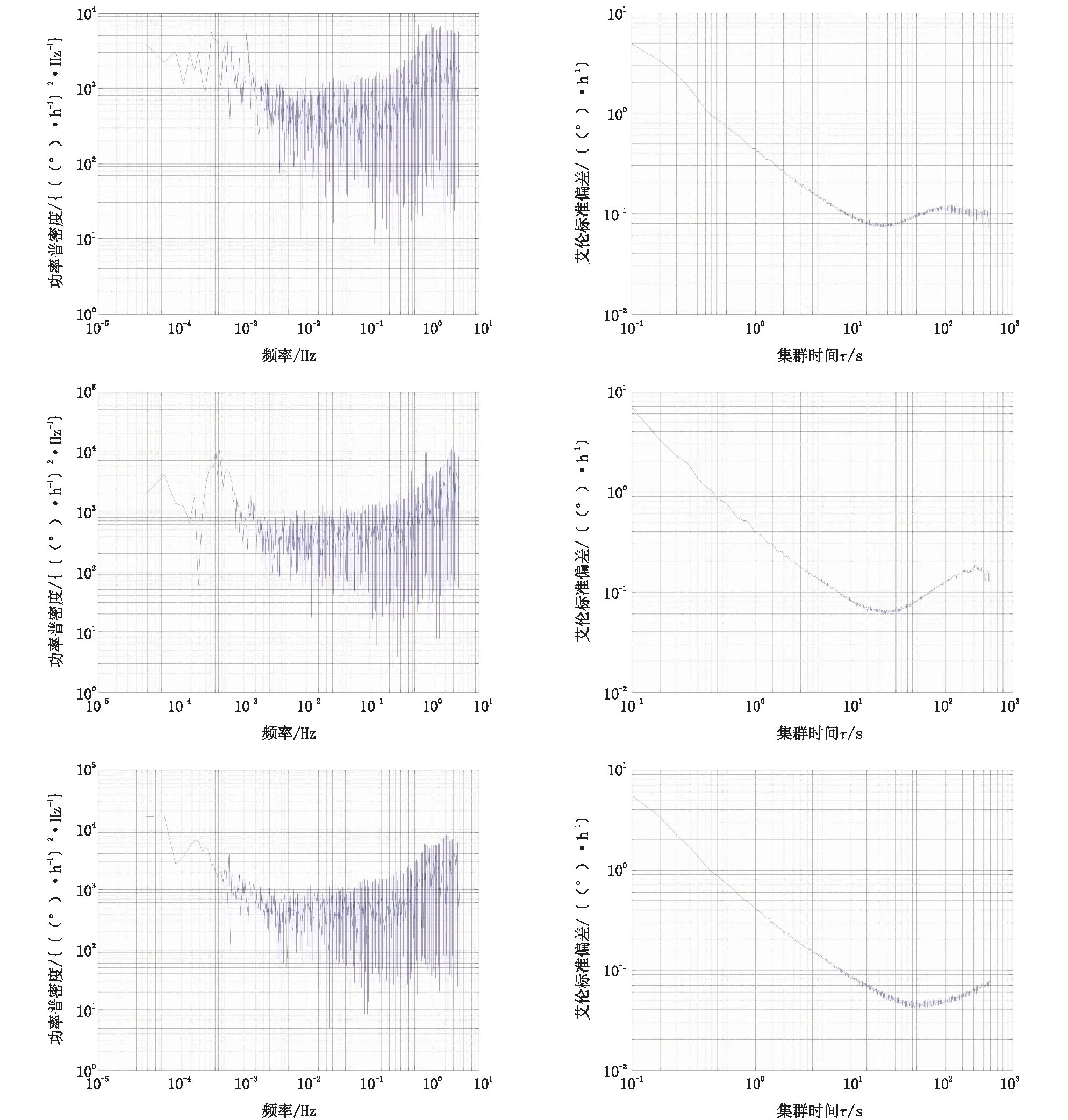
图8光纤陀螺随机误差功率谱密度和Allan标准差曲线

6 光纤陀螺惯测组合井下环境适应性研究

钻孔轨迹测量仪特殊的工作环境直接导致仪器需要承受振动冲击、地磁场、高温、以及重力场扰动等的影响。通常惯性仪表的误差约占系统误差的90%左右。环境条件是引起惯性仪表误差的主要因素，石英挠性加速度计作为另一种惯性器件，在测量领域已经得到很成熟的应用，这里主要讨论钻孔环境对光纤陀螺的影响。

6.1 仪器工作于地球表面下岩层，测量环境特点

(1)地表岩层存在天然的地磁场环境；

(2)地层内存在地层温度梯度(典型值3 ℃/100 m)，同时，仪器下井探管功耗也会导致保温瓶内温升；

(3)井壁的不规则，使运行过程中的仪器会承受特殊的力学环境。

主要针对仪器测量过程中光纤陀螺所承受的温度场环境以及地磁场环境影响进行分析。由于仪器运行缓慢，所承受的力学环境有限，对光纤陀螺造成的影响可忽略。

6.2 井下仪器系统内部的温度场在很大程度上影响着惯性仪表的输出特性

变化的环境温度引起的非互易性会给光纤陀螺带来大的漂移并限制其应用。

(1)光纤环引入热导致光路非互易性。

考虑光纤的温度效应，当光束以传输常数β(z)通过长度L为的光纤时，其相位延迟如式(17)所示：

(17)

式中：β0=2π/λ0——光在真空的传输常数；n——光纤有效折射率；n/T——石英材料的折射率温度系数；α——热膨胀系数；ΔT(z)——沿着光纤温度分布的变化量。

(18)

式(18)表明，光纤环由于温度效应引起的相位误差与光纤折射率随温度变化率成正比，与该段光纤上的温度变化率(即温度梯度)和与位置有关的权因子成正比，距光纤中点越远，权因子越大；对于一种光纤来讲，光纤折射率随温度变化率可以认为是常数。

(2)光纤陀螺温度补偿模型。

由于仪器测速较慢，温度变化引起的光纤陀螺标度因数误差可不作为重点项加以考虑，这里主要考虑光纤陀螺的零偏温漂特性。

实验采用仪器自加热的方式，将装配温度传感器的惯性测量单元置于保温瓶内，实时采集各温度点温度传感器输出和各惯性器件的输出，如图9所示。表示了各惯性器件随保温瓶内部温度变化的输出变化趋势。可以看出随着保温瓶内温度升高，光纤陀螺输出无明显的温度趋势项。即在井眼轨迹测量系统中，温度环境的变化对光纤陀螺性能无明显的影响。

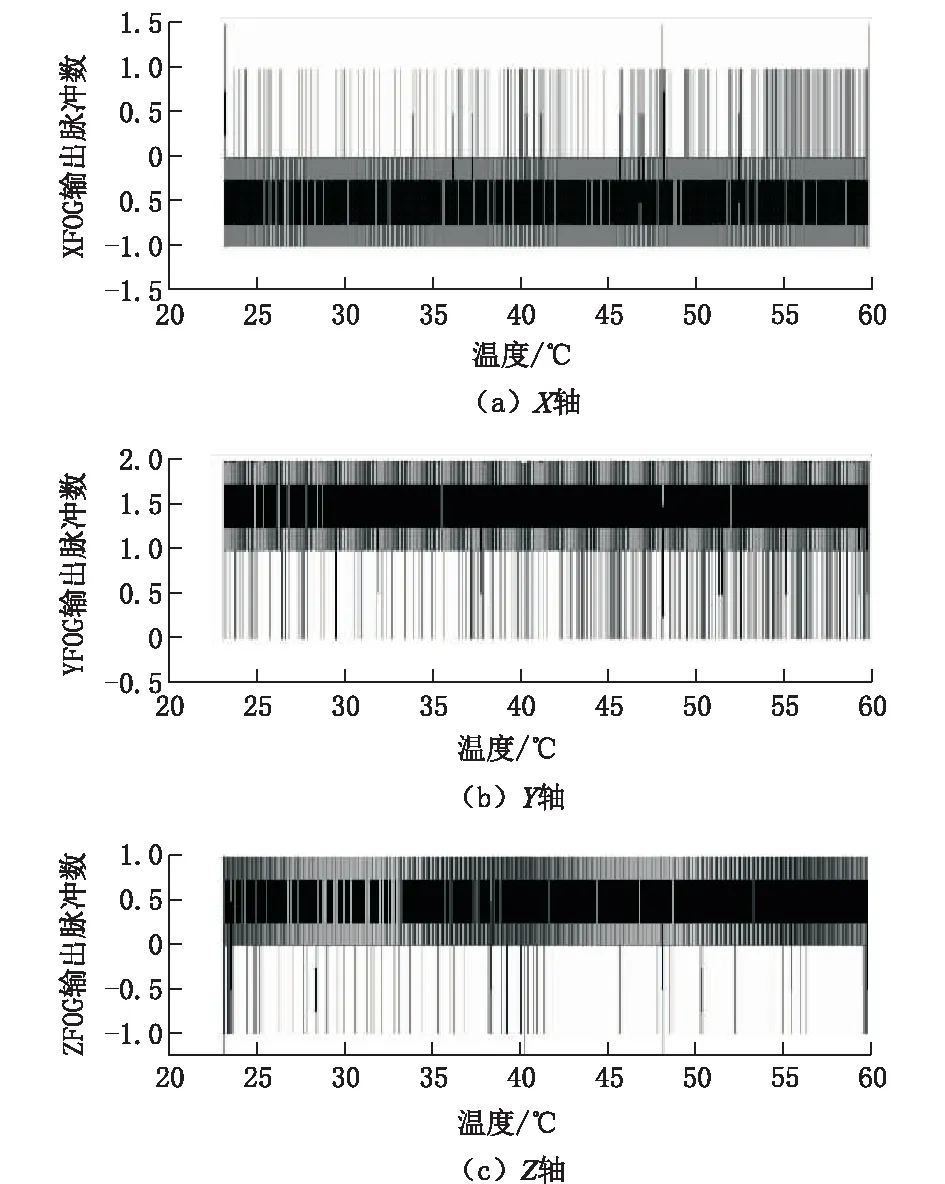
图9 光纤陀螺随温度的变化

6.3 井下磁场法拉第效应磁屏蔽

6.3.1 井下磁场环境描述

井眼轨迹测量系统用光纤陀螺所感受的磁场主要由主磁场(习惯上称为基本磁场)、地壳磁场和干扰磁场三部分组成。

6.3.2 光纤陀螺磁光法拉第效应模型

由于光纤本身可以敏感多种物理量，造成光纤陀螺的各种非互易误差。磁光法拉第效应就是其中之一，由于法拉第效应的非互易性，使得光纤陀螺中由于法拉第效应产生的误差相位与Sagnac 效应产生的相位无法区分，导致光纤陀螺的零位误差。

由于光纤陀螺检测的是光纤环中正反向传播光的非互易相位差，正反向传输光的相位差为：

(19)

令Δzi=Δz(i=1,2,…,n)且假设光纤环中的每一微段光纤的本征模传播参数满足函数ηi=η(z)、ηi′=η′(z)则可得：

(20)

对于高折射率光纤，可近似认为η(z)=η′(z)=Δβ/2，则：

(21)

将式(19)改为圆坐标系，即令z=rθ、ω=ω0sinθ代入式(21)得：

(22)

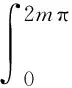
Δφ=4ω0rα/Δβ

(23)

因为ω0为单位长度上的法拉第效应引起的圆双折射ω0=VH，得：

Δφ=(4Vrα/Δβ)H

(24)

式中：V—— Verdet常数；H——磁场强度。

式(24)即为光纤陀螺的法拉第效应误差模型。可以看出光纤陀螺的磁效应误差为线性函数，与所加磁场的强度成正比。由于磁场强度为一矢量，即磁场强度有大小也有方向，可以由三个任意正交量的磁敏特性表示光纤陀螺的磁敏感特性。假设对光纤陀螺建立正交坐标系OXYZ，分别沿X、Y和Z轴方向施加磁场，测得此三个方向上的光纤环磁敏感性，则光纤陀螺磁敏感轴方向敏感到的法拉第效应误差为：

(25)

其中，光纤陀螺的磁敏感轴与所建X、Y和Z轴夹角，δX、δY和δZ分别为：

(26)

通过分析光纤陀螺法拉第效应误差模型可以得到以下结论：光纤陀螺受磁场影响，表现为一个附加的零位输出，其大小与所加磁场强度成正比；由于光纤陀螺存在空间的磁敏感轴，因此当光纤陀螺的磁敏感轴方向相对于磁场方向发生改变时，则光纤陀螺由法拉第效应误差影响的输出也将随之改变。

6.3.3 消除光纤陀螺磁敏感性的措施

采用屏蔽磁场来解决，一般分为低频磁场屏蔽和射频磁场屏蔽。对于光纤陀螺磁屏蔽，主要考虑低频(100 kHz以下)磁场屏蔽，其屏蔽原理是利用铁磁材料的高磁导率对干扰磁场进行分路。由磁通连续性原理可知，磁力线是连续闭合的曲线，磁通所构成的闭合回路称为磁路。

由于铁磁性材料的磁导率比空气大的多，所以铁磁材料的磁阻很小。将铁磁材料置于磁场中时，磁通将主要通过铁磁材料，通过空气的磁通将大为减少，从而起到磁场屏蔽作用。磁屏蔽设计时材料越厚，磁导率越大，磁屏蔽越好，这也决定了好的屏蔽体即昂贵又笨重；用铁磁材料做的屏蔽体不应有垂直磁力线方向的开口或缝隙，因为这会切断磁路，增大磁阻。

6.3.4 光纤陀螺磁屏蔽效果试验

本系统采用光纤陀螺进行磁屏蔽设计并进行了屏蔽效果试验。屏蔽材料选用铁镍钼超导磁合金，其磁导率高达105，厚度1.02 mm，磁屏蔽材料已经过退火处理。采用热真空炉成型，将三只光纤陀螺外罩表面全部覆盖这种屏蔽材料，由于安装面需要固定，在此不做处理。利用光纤陀螺磁敏感性试验装置对屏蔽前和屏蔽后的三只光纤陀螺施加等效地磁量级的磁场，测得磁屏蔽前后各轴光纤陀螺的补偿过地球自转角速率的零偏数据如表2所示。

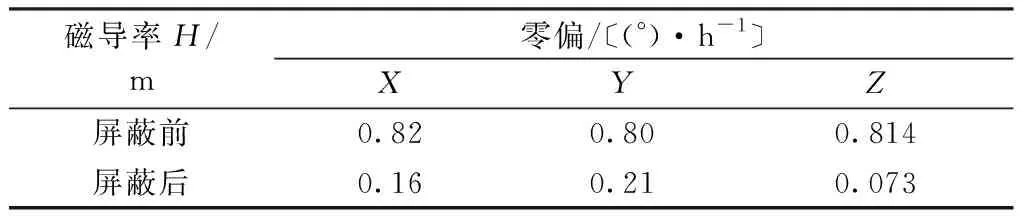
表2 屏蔽前后各轴光纤陀螺零偏

从上述测试结果可以看出，加磁屏蔽罩后，各陀螺由于外部磁场而导致零偏偏差的现象已经明显减小。

7 仪器外场标定技术研究

对于确定性误差可以通过精确标定加以补偿，本研究设计了适用于现场标定的“六位置二十四点”标定方法。本标定方法降低了对校验台的要求，不仅不需要校验台具有真北基准，而且对校验台的水平要求也较低。

7.1 陀螺组件模型

本系统所用的陀螺为角速率陀螺，通过积分便可得到转角。因此，在陀螺输出积分后，可理解为测角元件。因此，陀螺的数学模型方程为：

Ni/Ki=D0i+DXiAX+DYiAY+DZiAZ+

ωXcos(i，X)+ωYcos(i，Y)+ωZ

cos(i，Z) (i=1,2,3)

(27)

式中：Ni——敏感测量轴i单位时间的输出；Ki——敏感测量轴i的当量；D0i——测量轴i的零次项漂移系数；DXi、DYi、DZi——分别由AX、AY、AZ引起并与其成正比，作用在测量轴上的一次项漂移系数；AX、AY、AZ——组合坐标系加速度三个分量；ωX、ωY、ωZ——测试时地速在各轴的分量(已知)，使用时为载体运动角速度在组合系各轴的分量(要解算的量)；cos(i，X)、cos(i，Y)、cos(i，Z)——敏感测量轴i在组合系的方向余弦。

7.2 加速度计组件模型

加速度计的数学模型方程为：

Nj=K0j+KXjAX+KYjAY+KZjAZ

或

(Nj-K0j)/Kj=AXcos(j,X)+Aycos(j,Y)+

AZcos(j,Z)

(28)

式中：j= 1,2,3(1表示该轴与X轴靠近；2表示该轴与Y轴接近；3表示该轴与Z轴接近)；K0j——敏感测量轴j的零次项系数；Kj——敏感测量轴j的当量；KXj、KYj、KZj——Kj的方向数，即第j轴的当量沿组合坐标系的分当量；AX、AY、AZ——输入组合的加速度三维向量；Nj——加速度计敏感轴j单位时间的输出；cos(j,X)、cos(j,Y)、cos(j,Z)——敏感测量轴j在组合系的方向弦。

其中：

(29)

KXj=Kjcos(X,j)KYj=Kjcos(Y,j)
KZj=Kjcos(Z,j)

(30)

7.3 “六位置二十四点”编排

捷联组合可从模型方程系数定义出发，从总体及数学物理功能角度，可作如下编排：组合X、Y、Z三轴分别向上、向下共“六位置”绕铅垂线东南西北转1圈作4点采样以求其均值(6位置24点)。显然，该测试编排有如下特点：

(1)只考虑组合坐标系OXYZ(不涉及陀螺系)，并以此为基准正交翻转，作为位置测试采样点的数目达到了极限；

(2)相对于其他编排信息量大，且利用率高，处理计算结果统计性；

(3)该编排测试设备无须对北，首先将6位置的每个位置4点采样平均：

(31)

则原始数组N(24,6)转化为F(6,6)，这样设备免于对北的优点就显而易见了。

7.4 无真北测试中地球水平分量影响消除原理

设备无定向，即测试设备在测试间的放置无须考虑东南西北,这里要说明的是地速水平分量影响如何消除。

设：测试标定的起始位置与北向有一差角α，地速在逆时针每隔90°作一点采样的影响分别为(转台或方体旋转90°的位置精度，视测试允许误差而定，例如：≤5×10-5量级，精度为10″，主要还涉及到加速度计标定问题)：

Δ1=ωecosLcosα

(32)

Δ2=-ωecosLsinα

(33)

Δ3=-ωecosLcosα

(34)

Δ4=ωecosLsinα

(35)

式中：Δ1——第1点采样时地速北向分量在敏感轴上的投影；Δ2——转90°，第2点采样时地速北向分量在敏感轴上的投影；Δ3——再转90°，第3点采样时地速北向分量在敏感轴上的投影；Δ4——再转90°，第4点采样时地速北向分量在敏感轴上的投影。

对4点采样均值影响为:

Δ=Δ1+Δ2+Δ3+Δ4=0

(36)

7.5 调平不准引起的地速垂直分量及重力垂直、水平分量影响消除原理

设测试旋转平面与地平面夹角为γ(≤6′)，则地速的垂直分量影响：

Δ5=ωesinLcosγ

(37)

重力垂直分量影响：

Δ6=gcosγ

(38)

重力水平分量：

Δ7=gsinγcosφ

(39)

式中：φ——加速度计敏感轴与南北或东西夹角。

该影响与地速水平分量一样，通过绕垂线4点采样的均值将互相抵消，而当γ≤6′时的cosγ变化(≤1.5×10-6)完全可以忽略。因此,有关对北、调平问题有如下结论：

A.计算DOi、DXi、DYi、DZi时不会引起误差；

B.计算KOj、KXj、KYj、KZj时不会引起误差。

7.6 加速度组件系数标定

据数学模型式，从数组F(6,n)，可列出6个有关j敏感轴的方程，其中只有KOj、KXj、KYj、KZj未知，方程数多于未知数，可按多元回归求解。

设:

Fj=[F(1,j)F(2,j) …F(6,j)]′

(40)

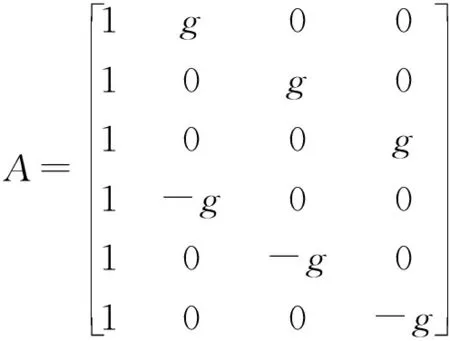
(41)

K=[KOjKXjKYjKZj]′

(42)

原方程为:

Fi=AK

(43)

回归系数为:

K=A-1Fi

(44)

或按下列关系式求之。

偏置(零次项系数)为：

KOj=〔F(1，j)+F(2，j)+…+F(6，j)〕/6

(45)

分当量(加速度分别沿X、Y、Z作用时j轴的输出当量，一次项系数)为：

(46)

则j轴当量(当加速度沿j轴方向作用时，单位速度的脉冲数)：

(47)

方向余弦：

(48)

7.7 陀螺组件系数标定

通过X/Y/Z向上时正反转360°即可得数组(6，m)，其中m为角速度测量轴的条数，若正反转时间基本相等(零次项误差可忽略)，则有关i轴沿X/Y/Z的分当量，每角秒脉冲数为：

(49)

(50)

(51)

角速度敏感轴的误差系数的标定从数组F(6,i)可列出6个有关i轴的方程，其中只有DOi、DXi、DYi、DZi未知。方程数多于未知数，可按多元回归求解：

F(6,i)/Ki=DOi+DXiAX+DYiAY+DZiAZ+

ωXcos(i，X)+ωYcos(i，Y)+ωZ

cos(i，Z) (i=1,2,3)

(52)

设：

(53)

式中：L——当地纬度。

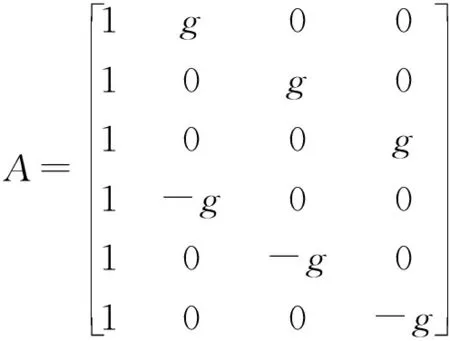
(54)

(55)

原方程为：

Fi=AD

(56)

回归系数为：

D=A-1Fi

(57)

也可以按下列关系式求之(i=1，2，3)：

(58)

综上所述，采用上述标定方法，降低了对现场标定设备的要求，具有很强的适应性，经现场试验表明，此标定技术满足技术指标要求。

8 存储式测控系统优化设计

8.1 测控系统功能

测控系统主要承担测量仪的电源管理(间歇供电)、数据通信、信息交换、数据存储、探管外温度测量等功能。测井斜的同时也钻孔温度，大大拓展了应用范围，并提高了仪器的使用效力。

8.2 测量控制系统设计

测控系统是整个测量仪器的主控中心，它通过RS232接口接收来自测量模块的倾角、方位角、工具面角、温度和时间等信息数据(通讯协议遵从数据测量模块的协议)，存储在外扩的FLASH存储器中，并对整个测量过程进行控制，同时带有系统电量分配控制、容错和保护功能，在返回地面后，能通过RS232接口将存储的数据传输给上位机，配合整个测量工艺流程、通过人机界面对测量过程参数、命令信息、数据信息等进行有效的设置，并读取信息数据、处理数据、存储信息数据等功能。硬件框图如图10所示。

图10 硬件框图

8.3 钻孔环境温度测量

钻孔环境温度测量，外部温度测量部分，使用高精度的PT100温度传感器及专用PT100测温转换器MAX31865芯片，该芯片可以直接通过SPI接口输出PT100的实际温度所对应的二进制补码，通过简单转换即可输出温度。测量范围：0～300 ℃,标定测量精度：±0.2 ℃。

8.4 测控软件设计与实现

本系统软件是集参数设置和数据导出等功能于一体的一个工具软件。

软件功能模块主要包括：串口通信、读取数据、参数设置、使用说明等四个模块，见图11。

硬件配置要求：CPU为酷睿2及其以上型号、内存为2G及以上、硬盘容量为40G或以上；

图11 软件系统结构

硬盘软件要求：操作系统为Windows7或Windows8、Windows10及以上版本；Net Framework 4.0；office2010及以上版本(需要完全安装excel组件)。

图12为程序流程图。它包括等时间间隔测量、定时测量二个流程。

图12 程序流程图

串口实现主控器与PC机软件、测斜仪之间的通信；RTC用于主控器的实时时间，该时间可以使用PC机软件进行设置；当模式1或者模式2时，钻孔环境温度传感器也工作；存储器为外挂512Kbit(64KByte)字节EEPROM存储器，用于存储来自测斜仪的数据。

PC参数设置界面如图13所示。

图13 参数设置界面

选中模式1连续，在点保存设置时，将会读取PC机当前时间，并将当前时间、图13中的首次测量时间、测量时间间隔、测量次数通过串口发送到主控器中，主控器将这些数据保存到单片机片内的EEPROM中，单片机根据EEPROM中的模式参数进入模式1的工作程式，其工作过程如图12程序流程图左间部分所示。

选中模式2定时，在点保存设置时，将会读取PC机当前时间，并将当前时间、图13中的T1～T24的时间(小时：分钟)通过串口发送到主控器中，主控器将这些数据保存到单片机片内的EEPROM中，单片机根据EEPROM中的模式参数进入模式2的工作程式，其工作过程如图12程序流程图右边部分所示。

注意：参数设置完成后，主控器不允许断电，否则时间数据会丢失，因为主控器上没有使用RTC电源。

读取数据:在主控器完成井下测量之后，可以将其通过RS232串口与PC机连接，然后读取保存在主控器FLASH中的数据，读取数据界面如图14所示。当选择了对应的串口号，并且连接成功以后，点击读取数据按钮，则会读出保存在主控器中的数据。

图14 读取数据界面

然后点导出数据，可将数据保存在一个TXT文本文档中用于数据分析和记录。

9 测试分析

通过测试，顶角、方位角计量测试见图15、温度计量测试见图16，测量仪机芯工作温度在-10～85 ℃范围内，加保温瓶后工作温度在-10～270 ℃范围内，承压管承压达120 MPa，方位角测量范围与精度为0°～360°(误差±1.5°,井斜>3°时)，井斜测量范围与精度为0°～90°(误差±0.15°)。实现了最大限度解决电池续航的问题，可以让光纤测斜测温仪持续工作超过4 h；实现存储光纤测斜仪采集的数据，且掉电不丢失；实现探管外部温度并存储，可用于地热探测等功能。

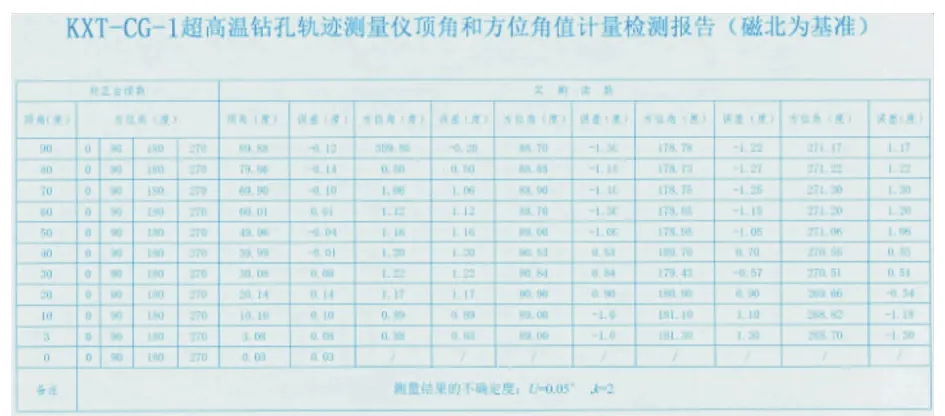
图15 顶角、方位角计量测试

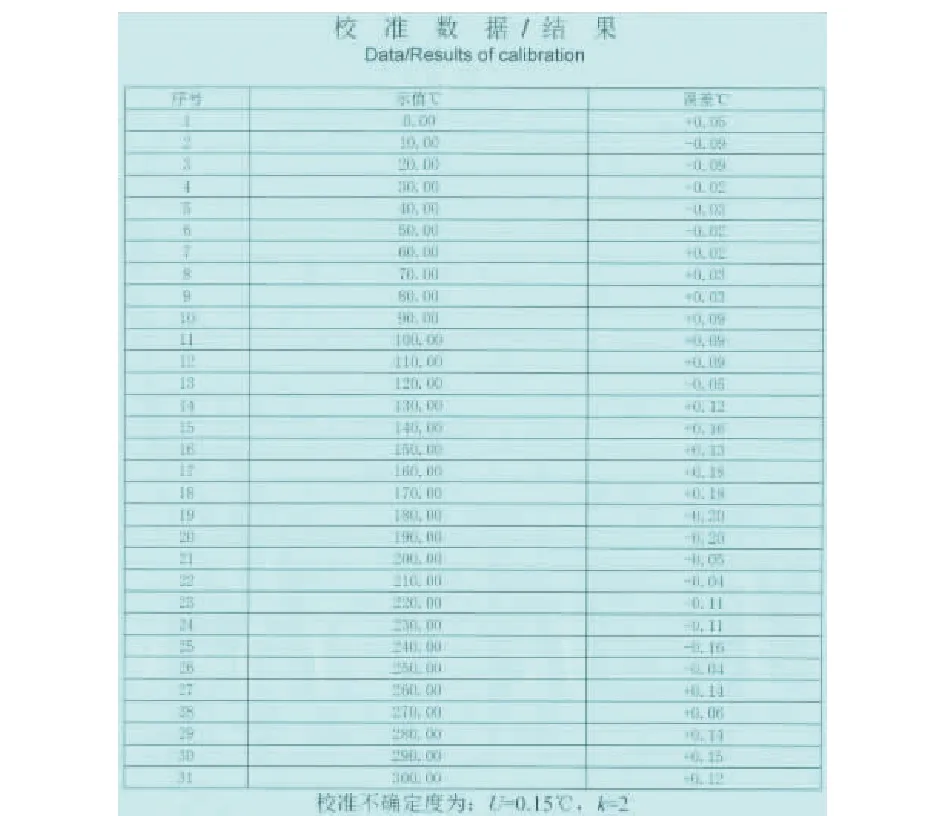
图16 温度计量测试

10 结语

通过本研究的实施，在三维光纤陀螺、三维石英挠性加速度传感器温度漂移和误差分析校正、测控技术等方面取得重大进展，研制出了耐温270 ℃、耐压120 MPa的超高温钻孔轨迹测量仪，解决了高温高压环境钻孔轨迹测量难题，完全满足高温高压地热能、科学钻探、深部矿产资源勘探以及深部油气资源勘探工程的需求，支持国家重要能源资源勘探工程。