载冷剂温度及流速对螺旋管蓄冰性能影响的模拟研究

徐唐富仪，吕静，常明涛，张继凯，赵德鹏



载冷剂温度及流速对螺旋管蓄冰性能影响的模拟研究

徐唐富仪1，吕静*1，常明涛1，张继凯2，赵德鹏2

（1-上海理工大学环境与建筑学院，上海 200093； 2-北京凯昆广胜新能源电器有限公司，北京 101300）

本文运用ANSYS软件模拟螺旋管蓄冰装置的蓄冰过程，研究载冷剂入口温度及速度变化对蓄冰性能的影响。结果显示，入口温度从269 K到263 K每下降3 ℃，240 min内水溶液液相率降低约14%，载冷剂温度越低，蓄冰性能越佳。载冷剂入口流速由1 m/s提高至3 m/s，每提高1 m/s，装置蓄冰率大致降低2%，降低不显著，载冷剂入口流速对装置蓄冰性能影响较小。本文对螺旋管的结构提出了优化方案，为螺旋管蓄冰装置的最佳运行工况提供理论基础。

螺旋管蓄冰装置；蓄冰性能；数值模拟

0 引言

在我国，每到夏季用电高峰期，电力会供应不足，同样的，夜间用电低谷期电力也未能被有效利用。针对这种现象，冰蓄冷空调应运而生，实现电负荷的“移峰填谷”[1]。近几年，人们对冰蓄冷系统的研究在不断推进。朱学锦[2]采用单工况制冰机组与常规制冷机组相结合的系统进行蓄冰、供冷，分析系统在投资和运行费用方面的优势。梁坤峰等[3]也基于温湿度独立控制的概念，将冰蓄冷系统与毛细管辐射及地源耦合，降低能耗、提高舒适度。其中，冰蓄冷空调的蓄冰方式有多种，螺旋管的特殊结构使得流体在垂直流动方向上会产生二次环流，从而增强流体之间的换热能力。

许传龙等[4]建立了直接蒸发式盘管结冰过程的动态数学模型，运用有限差分法进行数值求解。张曼等[5]提出了分离式螺旋热管蓄冷空调系统，研究管外冰层厚度、蓄冰率等随时间的变化关系。马永涛[6]搭建了蓄冰系统实验台，对内融式盘管蓄冰系统进行实验研究，并利用Matlab搭建蓄冰系统仿真实验台，分析不同管材、管径对蓄冰、融冰性能的影响。常明涛等[7]采用中间加装直管段的方式对螺旋管蓄冰装置进行优化。

但上述研究中缺少运行参数变化对螺旋管蓄冰装置的影响。本文利用ANSYS软件模拟蓄冰过程，研究载冷剂温度及速度变化对蓄冰性能的影响，重点阐述运行参数变化对螺旋管这种结构的影响。同时，提出对螺旋管结构的优化方案，为螺旋管蓄冰的最佳运行工况提供理论基础。

1 蓄冰模型的建立

1.1 蓄冰装置换热模型

1.1.1 蓄冰装置的几何模型

本模拟装置如图1所示：内部螺旋盘管设置为5圈，圈径180 mm，管径为12.7 mm×0.7 mm，螺距100 mm；外部冰桶直径为250 mm，高度为600 mm。

图1 蓄冰装置几何模型

1.1.2 蓄冰装置换热过程数学模型

蓄冰装置内部存在相变过程，且蓄冰过程存在显热蓄冰、潜热蓄冰两个过程，为了方便数学模型的建立，提出合理假设[8]：

1）相变材料是均匀、各向同性的；

2）假设相变过程中，比容、导热系数、密度等为常数，不随相变过程发生改变；

3）管内载冷剂是不可压缩的牛顿流体；

4）蓄冰装置圆筒外壁面绝热；

5）忽略管壁的导热热阻和蓄热能力。

基于上述的假设，列出以下数学方程[9-12]。

相变工况连续性方程：

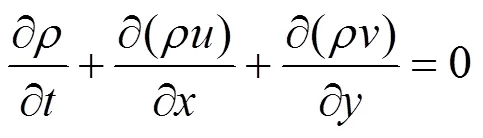
相变材料的能量方程：

相变材料的动量方程：

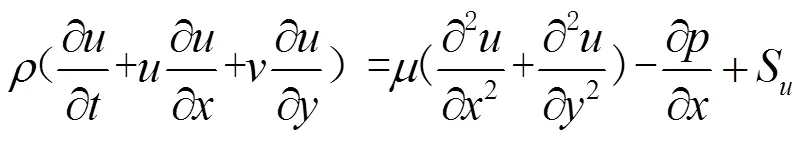
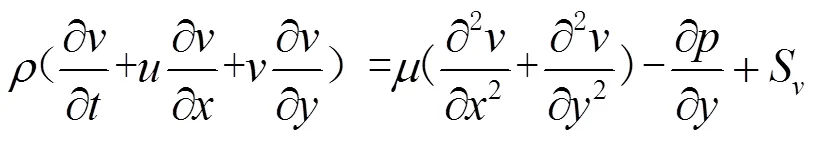
式中：

——密度，kg/m3；

——流体速度，m/s；

——流体运动黏度，Pa·S；

——任意时刻的焓值，kJ/kg；

h——基准焓值（初始），kJ/kg；

——动量源项；

——液相分数；

C——定压比热容，J/(kg·K)；

——潜热，J/kg。

1.2 螺旋盘管蓄冰过程换热计算

由于盘管蓄冰槽传热过程较为复杂，做出以下假设，简化数学模型[13-14]：

1）管外水溶液的热传导假设为导热过程，忽略内部的自然对流对换热的影响；

2）盘管、冰层以及外侧水层，几何结构为同心圆环，冰层的传热按纯导热处理；

3）设定水溶液接近冰点温度0 ℃，冰层水层接触面为0 ℃；

4）固液相变过程中，忽略密度差引起的溶液体积变化。

1.2.1 显热蓄冷计算

盘管第个单元段冷媒的换热量：

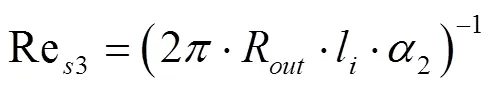
式中：

——换热系数与换热面积乘积，W/℃；

T——第i个单元段水溶液温度，℃；

T——第i个单元段冷媒溶液温度，℃；

R——盘管内径，m；

R——盘管外径，m；

l——单元段长度，m；

1——乙二醇溶液与盘管内壁面之间对流换热系数，W/(m2·℃)；

——盘管导热系数，W/(m2·℃)；

2——水与盘管外壁面之间对流换热系数，W/(m2·℃)。

1.2.2 潜热蓄冷计算

水溶液温度已达到冰点温度0 ℃，发生相变现 象逐渐形成冰层。盘管蓄冰过程的数学描述：

管内载冷剂与管外冰层间换热量Q：

式中：

Q——管内载冷剂与冰层间换热量，W；

D——换热温差，℃；

t——水溶液冰点温度，℃；

t——载冷剂平均温度，℃；

r——管内径，m；

h——管内对流换热系数，W/(m2·K)；

k——管壁导热系数，W/(m2·K)；

k——冰层导热系数，W/(m2·K)。

2 蓄冰过程数值模拟及验证

本文采用非结构四面体进行网格划分（图2），交界面采用“Merge”方式进行节点重合。模型整体采用较大的单元网格体进行划分，针对螺旋管壁面等重要部位采用局部加密的方式。

图2 非结构网格划分

鉴于现有实验条件的约束，本文选取参考文献[15]列出的各项实验参数，并选取温度测点14#、16#、19#测点作为参考点，对上述实验工况进行数值模拟（图3）。可以看出：模拟条件下温度曲线同文献[15]实验条件下温度曲线基本吻合，150 min后变化趋势保持一致。由两者温度数值上的差异可知，在实验过程中难以做到绝对的绝热，必定存在热量的损失；实验中会产生测量设备所引起的误差。综上所述，本文所建立的模拟模型具有合理性，可根据此模型做后续研究。

图3 文献值与模拟值对比图

3 参数变化对蓄冰过程的影响

3.1 载冷剂入口温度变化对蓄冰的影响

采用单一变量法，当载冷剂乙二醇入口流速为1 m/s、水溶液起始温度为5 ℃时，单独改变乙二醇溶液的入口温度，模拟分析乙二醇溶液入口温度为263 K、266 K和269 K时螺旋管的蓄冰性能。

通过模拟结果可发现（如图4示）：240 min内，当载冷剂乙二醇溶液温度较低时，蓄冰装置内液相率较低，蓄冰性能更佳。269 K时，蓄冰桶内的平均液相率为78.1%；266 K时平均液相率为67.9%；263 K时平均液相率为58.4%，故载冷剂温度每下降3 ℃，液相率降低约14%。这是由于在蓄冰过程中，水溶液初始温度相同，在相变发生时，冰水溶液温度为0 ℃，载冷剂乙二醇溶液与相变材料水之间的换热温差为D263K>D266K>D269K。冷热流体之间的温差为换热提供动力，故温度越低、温差越大、换热能力越强。

图4 不同入口温度对应的液相率云图

随着蓄冰过程的进行，单位蓄冰量逐渐减少。这是由于在蓄冰初期，冰层厚度的增加使得冰层与水的换热面积增大，从而增加换热量；然而蓄冰中后期，随着冰层厚度的增加，冰层产生的热阻越来越大，成为主要热阻，导致单位蓄冰量的减小。

利用Matlab对此蓄冰过程中管内热阻的变化进行分析，结果如图5。以入口温度263 K为例，管内对流换热热阻及盘管导热热阻基本不变，冰层导热热阻随着蓄冰过程的深入，从0增长至0.122 (m·K)/W。故随着蓄冰过程的进行，换热整体热阻逐渐增大，单位蓄冰量减小。

3.2 载冷剂入口流速变化对蓄冰的影响

当载冷剂乙二醇起始温度为263 K，水溶液起始温度为278 K时，单独改变乙二醇溶液的入口速度，模拟流速为1 m/s、2 m/s、3 m/s时对相变蓄冰过程的影响。

图6为Fluent的模拟结果可发现：240 min内，随着载冷剂乙二醇溶液流速的提高，蓄冰装置内液相率变低，蓄冰性能有所提升，但提高幅度并不明显。当载冷剂入口流速为1 m/s时，蓄冰桶内的平均液相率为58.4%；2 m/s时平均液相率为57.7%；3 m/s时平均液相率为56.8%，故载冷剂的流速每提高1 m/s，其液相率降低约2%，未显著下降。

图5 蓄冰过程中热阻变化

图6 不同入口速度的液相率云图

从强化换热的角度分析，随着入口流速的提高，增强了管内的扰动，换热效率应该有明显的提升，但是在模拟中却未发现换热量有显著提升（图7）。分析原因如下。

1）管内流体的温度场和速度都比较均匀，故流动阻力和对流换热阻力主要存在于边界层底层中。但由于螺旋管特殊的形状，流体在螺旋管中流动时受曲率和离心力的影响形成二次环流，在近壁面处又由于扰动产生旋涡流动。这样的特殊结构不断破坏边界层，较直管已增强了换热，也使得小幅度的提高流速对整体换热影响不大。

2）利用Matlab从热阻的角度进行分析：蓄冰初期为显热交换，冷热流体之间的换热热阻由管内对流换热热阻、盘管导热热阻两部分组成。流速的改变可影响管内对流换热热阻这一因素，故蓄冰初期时，载冷剂入口流速的增大对蓄冰性能有所影响。但随着蓄冰过程的进行，进入潜热交换阶段，此时冷热流体之间的换热热阻有管内对流换热热阻、盘管导热热阻、冰层导热热阻，且冰层导热热阻迅速成为换热过程中的主要热阻，对流换热热阻影响较小。伴随着冰层厚度的增加，整体换热热阻增大，冷热流体间换热能力大幅削弱，单位蓄冷量也逐渐降低。

图7 管内对流换热热阻占整体热阻百分比

3.3 蓄冰性能随时间的变化

本文通过延长模拟时间，研究蓄冰过程中的液相率分布（图8），提出对螺旋管结构的优化方案。当载冷剂乙二醇起始温度为263 K，入口速度为1 m/s，水溶液起始温度为278 K时，分别模拟240 min、300 min和360 min时，相变蓄冰过程的变化。

图8 不同蓄冰时间的液相率云图

随着蓄冰过程的进行，螺旋管外侧的冰层厚度逐渐增加，在360 min时，螺旋管底部位置出现了冰层相叠的现象。当继续蓄冰时，就造成了无效蓄冰、浪费电能，也不利于融冰的现象。因此，当管径较大时，螺距可适当加大，避免相邻冰层的重复结冻，保证结冰的均匀度；当管径较小时，螺距则可以适当减小。同时，可观察到中间区域的液相率较高，可减小螺径，使得中间区域的结冰更均匀。

4 结论

1）载冷剂入口温度对蓄冰性能具有较大影响，入口温度从269 K到263 K每下降3 ℃，液相率降低14%。蓄冰过程中，由于冰层热阻的增加，单位蓄冰量逐渐减小。

2）载冷剂入口流速对蓄冰性能影响较小，入口流速由1 m/s提高至3 m/s时，装置蓄冰率大致降低2%，降低不明显。螺旋管自身的特殊结构使得流体能够不断破坏边界层，小幅度的流速提升对整体换热影响不大。从热阻角度分析，流速的增大也仅能对蓄冰初期有所影响。

3）观察冰层的均匀度可发现：当管径较小时，螺距可适当减小；当管径较大时，螺距则可以适当加大，避免相邻冰层的重复结冻；可适当减小螺径，保证各个区域结冰的均匀度。

[1] 刘琳. 冰蓄冷空调技术的应用及前景[J]. 技术与应用, 2015(1): 100-101.

[2] 朱学锦. 某金融中心冰蓄冷系统的应用与经济性分析[J]. 制冷技术, 2016, 36(4): 72-77.

[3] 良坤峰, 任岘乐, 贾雪迎, 等. 冰蓄冷辐射空调系统运行优化与能耗分析[J]. 制冷技术, 2014, 34(6): 68-73.

[4] 许传龙, 孔明, 卢勇, 等. 蓄冷系统水平冰盘管外结冰数值模拟及分析[J]. 建筑热能通风空调, 2005, 24(1): 13-17.

[5] 张曼, 方贵银, 吴双茂, 等. 分离式螺旋热管蓄冰过程动态特性模拟[J]. 低温与超导, 2008, 36(8): 1-4.

[6] 马永涛. 内融式盘管蓄冰系统实验研究[D]. 天津: 天津大学, 2007.

[7] 常明涛, 吕静, 高强, 等. 螺旋管式相变蓄冰装置的结构优化[J]. 建筑节能, 2017, 45(315): 114-152.

[8] 钟亮, 潘阳. 加金属丝水平单元管蓄冰数值模拟[J]. 华东交通大学学报, 2011, 28(5): 35-40.

[9] SRINIVASAN P S, NANDAPURKAR S S, HOLLAND F A. Pressure drop and heat transfer in coils[J]. Chemical Engineering, 1968, 218: 113-119.

[10] 张周卫, 李跃, 汪雅红, 等. 恒壁温工况下螺旋管内流体强化传热数值模拟研究[J]. 制冷与空调, 2016, 16(2): 43-48.

[11] 王昊. 采用新型相变材料蓄热桶蓄放热特性数值计算方法探讨[D]. 北京: 北京工业大学, 2003.

[12] 张云婷, 云和明, 张艳玲, 等. 壳管式相变蓄热装置的数值模拟[J]. 制冷与空调, 2013, 27(4): 329-334.

[13] 方贵银. 直接蓄冰系统蓄冷过程动态模型研究[J]. 热能动力工程, 1999(2): 92-94.

[14] 赵思越, 克红娟, 林文胜, 等. 基于L-CNG加气站冷能利用的蓄冰槽性能模拟与分析[J]. 制冷技术, 2017, 37(4): 34-40.

[15] 姜佳伟. 竖直管加丝蓄冰过程的数值分析与实验研究[D]. 南昌: 华东交通大学, 2012.

Simulation Study of Impact of Refrigerant Temperature and Flow Rate on Ice Storage Performance of Spiral Tube

XU Tangfuyi1, LÜ Jing*1, CHANG Mingtao1, ZHANG Jikai2, ZHAO Depeng2

(1-School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China; 2-Beijing Kaikun Guangsheng New Energy Electric Appliance Co., Ltd, Beijing 101300, China)

The software, ANSYS, was used to simulate the ice storage process of the spiral tube ice storage device. The impact of inlet refrigerant temperature and flow rate on the ice storage performance was studied in this paper. Results show thatliquid fraction decreases by 14% in 240 minutes when the inlet temperature drops every 3 ℃ from 269 K to 263 K. The result indicates the better ice storage performance at a lower temperature. Liquid fraction unnoticeably decreases by 2% when inlet flow rate rises every 1 m/s within the range of 1~3 m/s, which shows less important impact of inlet flow rate on ice storage performance.Meanwhile, the spiral tube structural optimization has been proposed as the theoretical basis for the optimal operating conditions.

Spiral tube ice storage device; Storage performance; Numerical simulation

10.3969/j.issn.2095-4468.2018.04.107

*吕静（1964-），女，博士，副教授。研究方向：节能技术及CO2热泵空调系统。联系地址：上海市杨浦区军工路516号484信箱，邮编：200093。E-mail：lvjing810@163.com。