基于减法聚类和支持向量机的故障诊断方法研究

陈玲，陈志杰，杜志敏，晋欣桥，方兴



基于减法聚类和支持向量机的故障诊断方法研究

陈玲，陈志杰，杜志敏*，晋欣桥，方兴

（上海交通大学制冷与低温工程研究所，上海 200240）

依据GB/T 5773-2004，本文搭建了容积式制冷剂压缩机性能试验台，其精度及可靠度完全取决于传感器的可靠性。本文提出采用减法聚类和支持向量机相结合的方法对制冷剂压缩机性能试验台传感器进行故障检测。减法聚类将试验数据的各种工况加以区分，然后根据各类已区分的工况，利用支持向量机对运行数据进行故障检测。实验结果表明，本文提出的减法聚类和支持向量机相结合的方法可以对压缩机性能试验台的传感器固定偏差故障进行有效的故障检测，故障检测准确率在90%以上。

压缩机试验台；减法聚类；支持向量机；故障检测

0 引言

能源问题日益成为当今世界共同关注的问题，也是今后长期存在的问题。为解决这个问题，人们正致力于寻找新能源和提高能源利用效率。我国建筑能耗占社会总能耗的20%~25%，发达国家建筑能耗占社会总能耗的30%~40%[1]，建筑能耗占社会总能耗的比重较大，并且有较大的节能潜力。为了实现节能和提高室内空气品质，空调系统正变得越来越复杂，这不但导致空调系统的故障发生比较频繁，而且增加了故障检测与诊断（Fault Detection and Diagnosis，FDD）的难度。故障会影响空调系统的正常运行，进而导致空调系统能耗的增加、室内热舒适性的降低、设备使用寿命的缩短和设备维修费用的增加。理论研究与实验调查表明，通过实施故障诊断和优化空调系统的运行，可以降低20%~30%的建筑能耗[2]。通过成功实施故障检测与诊断，可以减少10%~40%的空调系统能耗[3-4]，其节能潜力主要由建筑用途、设备新旧、设备状态和设备维护情况等因素决定。

目前，测量控制的可靠性在航天[5]、核电[6]、智能高速公路[7]、化工[8]等领域发展较为完善。但在制冷领域中，发展较为缓慢。实际制冷系统中，温度、压力、流量传感器不仅表明运行条件，也能起到反馈作用，控制器可能会被误导而导致故障[9]。若能及时检测出传感器故障，不仅可减少系统设备损耗，而且能节约能耗。

本文提出采用减法聚类和支持向量机相结合的方法对制冷剂压缩机性能试验台传感器进行故障检测。其中，减法聚类将实验数据的各种工况加以区分[10]，支持向量机对已区分工况的运行数据进行故障检测。

1 研究对象

本文的压缩机性能试验台[11]是依据GB/T 5773- 2004[12]容积式制冷剂压缩机[13]性能试验方法搭建的。本文采用排气管制冷剂气体流量计法（D方法）为主测量方法，以制冷剂气体冷却法（J方法）为辅助测量方法。计算机监测和控制系统用于自动控制、数据采集和自动记录以及打印报告等功能。计算机监测和控制系统采用美国国家仪器（National Instruments）控制模块，用LabView编程。压缩机试验台原理简图如图1所示，其中Pi、Ti分别表示传感器测量所得的压力和温度。图2为压缩机试验台实物图。

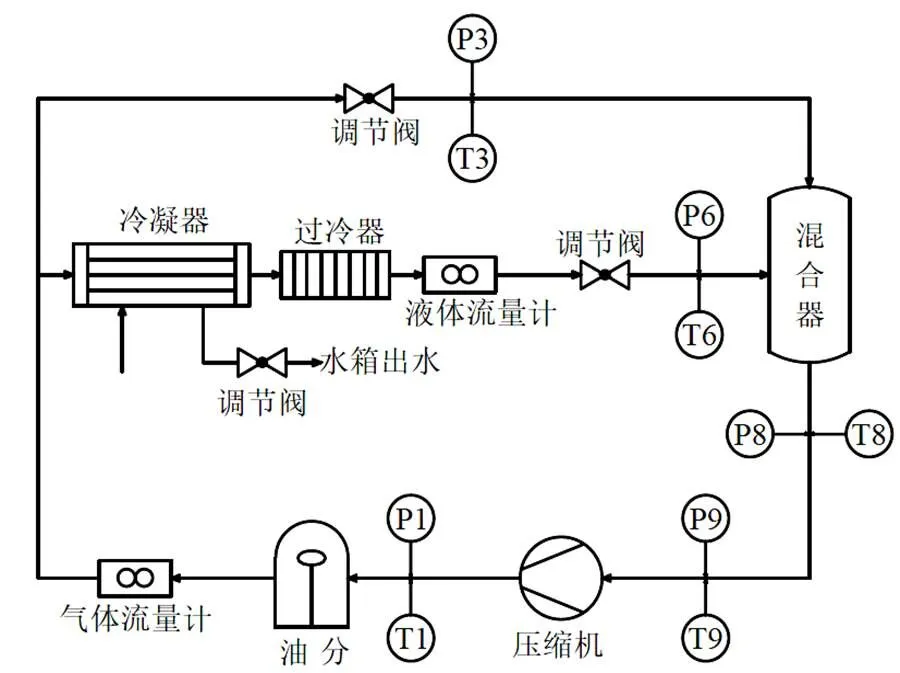
图1 压缩机试验台原理简图

图2 压缩机试验台实物图

D方法测量排气制冷剂的质量流量（图1中气路流量计所测）和吸气压力温度（由此可以得到进入压缩机时，制冷剂蒸汽的实际比容）等参数。流量计安装于测试系统排气侧的管道上。在测试的时候，需要控制的参数为：吸气压力、吸气温度和排气压力。

J方法测量的基本原理为：通过将系统高压一侧的部分制冷剂气体冷凝，得到这部分的流量（图1中液路流量计所测），再使这部分制冷剂在气体冷却器内的低压下蒸发。这部分制冷剂可以将余下的循环制冷剂蒸气冷却，这部分蒸气的压力是经过降压的。从这整个过程可以计算得到制冷剂的总流量。在进行了漏热量修正后，已冷凝的制冷剂质量和未冷凝的制冷剂质量之比等于在气体冷却器中两股蒸气比焓变化之比的倒数。

2 故障检测方法

2.1 减法聚类原理

减法聚类是把所有的样本点作为聚类中心的候选点，是一种快速而独立的近似聚类方法，其计算量与样本点数目成简单的线性关系，且与所考虑问题的维数无关。

减法聚类是一种爬山法，它首先计算每个样本点的密度指标，如果该样本点周围的点多，则密度指标大，将密度指标最大的样本点选为第一个聚类中心。选定第一个聚类中心后，其它样本点的密度指标根据样本点距离第一个聚类中心的距离作相应调整，离第一个聚类中心越近的样本点，其密度指标减小得越多，下一个聚类中心选在调整后的密度指标最大的样本点上；然后再对所有样本点的密度指标进行调整，寻找下一个聚类中心，依次进行，直到找到足够多的聚类中。

令= {x，x，x} ϵR表示样本点集，是样本的个数。减法聚类实现步骤如下。

a）首先对于中的每一个点x，计算其密度指标：

选取密度指标最高的数据点x为第一个聚类中心。其中r为正数。显然，如果一个样本有多个邻近样本，则该点具有高密度值。半径r定义了该点的一个邻域，半径以外的样本对该点的密度指标贡献甚微。

b）假定x为第次选出的聚类中心，密度指标为D，其他数据点x（x≠x）的密度指标按公式(2)进行修正，选出密度指标最高的数据点作为新的聚类中心。常数r定义一个密度指标函数显著减小的邻域，邻域中靠近第个聚类中心的样本点的密度指标显著减小，这些点不太可能成为下一个聚类中心。常数r通常大于r，为了避免出现相距很近的聚类中心，一般取r= (1.2~1.5)r。

c）重复上述修正过程，判断公式(3)是否成立。若不成立，则转b）；若成立则退出。其中0<<1是事先给定的参数，决定了最终产生的初始化聚类中心数目。

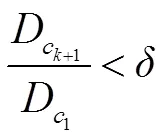
减法聚类中心出现的顺序由密度指标决定，密度指标越大出现得越早，也越可能是合理的初始聚类中心。因此在对聚类数为的检测中，只需以减法聚类产生的前个聚类中心作为新的初始中心就可以了，不需要再重新进行初始化，从而提高聚类的效率。

2.2 支持向量机

支持向量机的核心思想是寻找一个满足分类要求的最优分类超平面，该超平面在保证分类精度的同时，应使分类间隔最大化[14-17]，如图3所示。在进行线性分类时，将分类面取在离两类样本距离较大的地方；进行非线性分类时通过高维空间变换，将非线性分类变为高维空间的线性分类问题。

图3 最优超平面示意图

在高维特征空间中寻求最优分类超平面的过程及方法与线性可分SVM情况类似，只是以核函数取代了高维特征空间中的点积，从而大大减少了计算量与复杂度。映射到高维特征空间后对应的对偶问题变为：

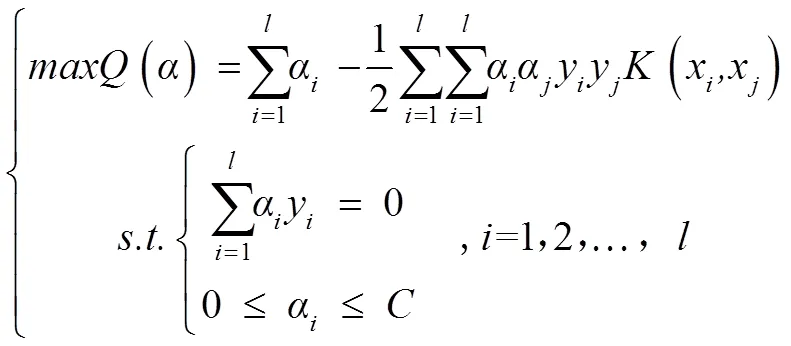
设*=(1*,2*,…,*)是式(5)的解，则：

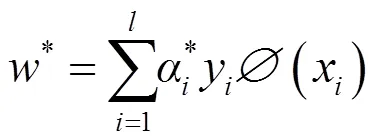
从而最终的最优分类函数为：

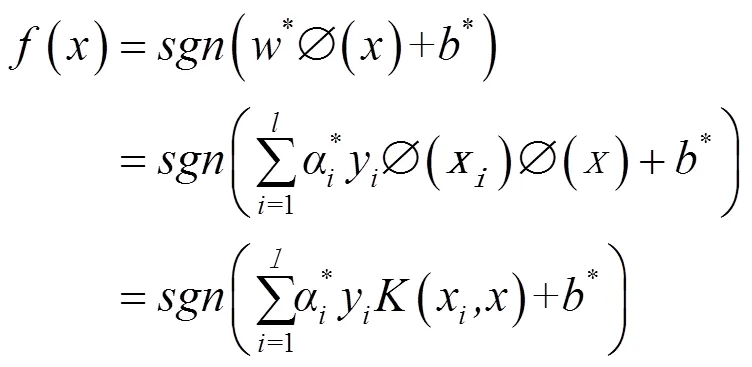
容易证明，解中将只有一部分（通常是少部分）不为零，非零部分对应的样本x就是支持向量，决策边界仅由支持向量确定。

3 压缩机试验台故障检测及结果分析

3.1 故障检测逻辑

压缩机试验台故障检测流程图如图4所示。

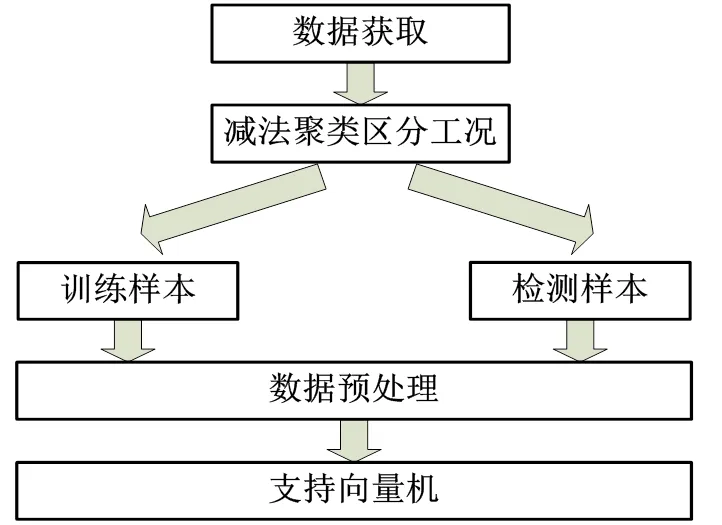
图4 故障检测流程

获取数据之后，先通过减法聚类自适应区分工况，将数据按工况进行分类。数据在进行模型训练或测试之前需要进行数据预处理，包括数据的标准化和参数提取等，然后利用支持向量机建立模型，用训练样本对模型进行训练，再通过对测试样本进行检测，并分析检测结果。

3.2 基于减法聚类的工况判别

根据压缩机试验台特点及测量到的实验数据，建立减法聚类模型。该聚类模型采用了6个参数，分别为压缩机型号、频率、电压、冷凝温度、蒸发温度和过热度。该聚类模型所选用的参数可明确反映一个工况，由此可知，聚类模型参数的选取是合理的。

容积式制冷剂压缩机试验台的数据都是06N机型的，收集到的数据主要有6个工况，如表1所示。

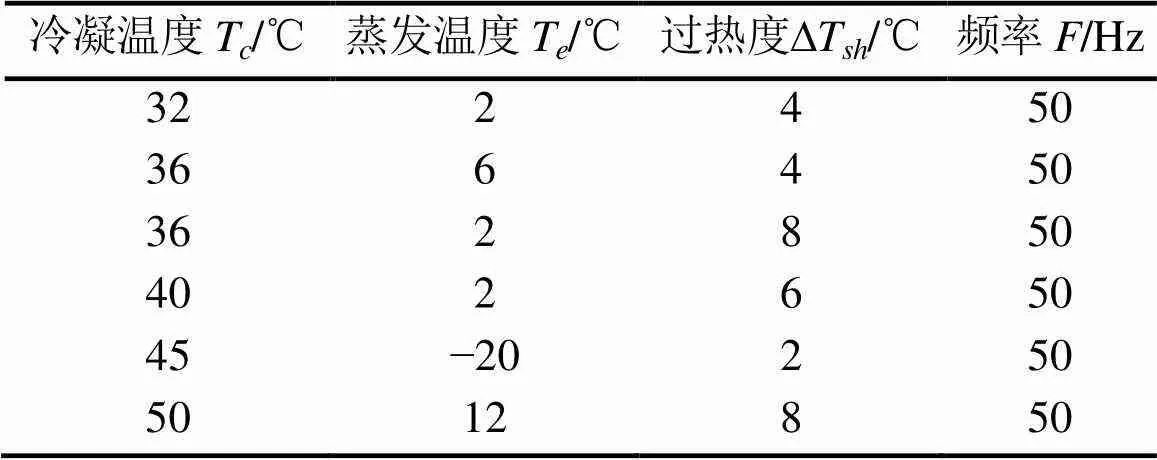
表1 06N型压缩机数据工况

由于数据都来自06N机型的压缩机，所以数据的机型和电压一致。06N机型的压缩机为定频压缩机，所以数据的频率一致。仿真结果以图的形式呈现，现将六维聚类模型简化为三维模型——冷凝温度、蒸发温度、过热度。后期如果出现其他机型，可使用原先的六维聚类模型自适应识别工况。

由于原数据中的冷凝温度、蒸发温度、过热度之间的数值相差较大，故先将数据归一化之后再进行减法聚类。通过多次仿真，调整参数为0.055时，能完全自适应识别全部工况。图5为所有工况下稳定数据的聚类结果，如果再增加一种工况下的稳定数据，该仿真模型也能自动识别其工况。

图5 减法聚类结果

3.3 基于支持向量机的故障检测

通过减法聚类分类后，获取的数据可以按工况分类。将训练样本和检测样本按工况分类后，建立支持向量机模型。本文选取了18个具有代表性的参数建立模型，分别为：频率（）、压缩机出口压力（1）、压缩机出口温度（1）、气液混合器前气体压力（3）、气液混合器前气体温度（3）、气液混合器前液体压力（6）、气液混合器前液体温度（6）、气液混合器出口压力（8）、气液混合器出口温度（8）、压缩机入口压力（9）、压缩机入口温度（9）、总质量流量（）、主气路质量流量（气）、主液路质量流量（液）、制冷量（）、功率（）、电压（）和电流（）。建立初步参数模型如下所示：

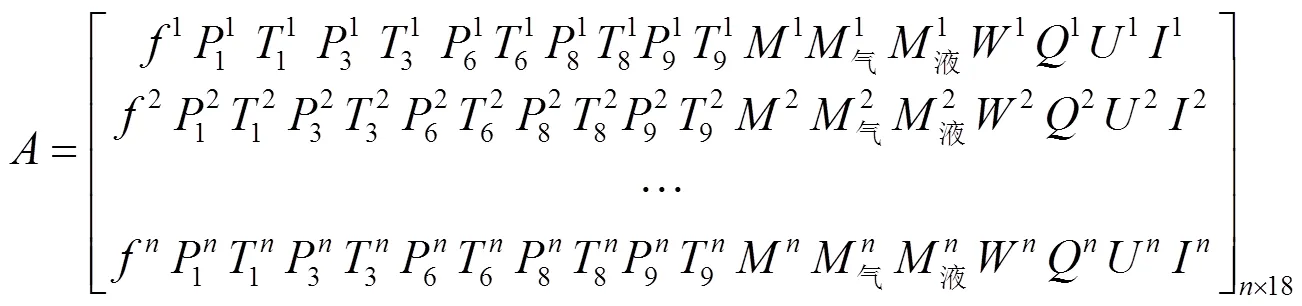
本文在同一稳定工况下，引入传感器固定偏差故障，选取其中一天的数据作为训练样本，后面两天的数据作为检测样本，并分别将数据进行归一化处理。稳定工况下，分别引入P1和P9传感器10%和20%的固定偏差。

在创建和训练支持向量机故障诊断模型时应考虑核函数及相关参数对模型性能的影响。本文采用径向基核函数(x,x)。核函数、映射函数以及特征空间都一一对应，确定了核函数也就隐含地确定了映射函数和特征空间。模型的性能由参数（,）决定，其中是惩罚因子，表征重视离群点程度，是RBF核函数中的方差，参数（,）优化可以使得松弛变量最优化。的作用是在确定的数据子空间中调节学习机器的置信区间范围，对于不同的数据子空间，惩罚因子的最优化结果是不同的，而参数的改变实际上是隐含地改变映射函数，从而改变样本数据子空间分布的复杂程度[18]。本文采用5折交叉验证来选取最优的（,），参数取值范围：lg()为[−10, 10]，lg()为[−10, 10]，最后获得的最佳参数组合为（1,024, 8）。

将第一天的故障数据作为训练数据，其中数据标记为0，故障数据标记为1。采用最优性能参数（,）训练模型，将后两天的数据用于支持向量机模型检测，可以检测出数据是否发生故障。故障检测结果如表2所示。正确表示样本数据被检测诊断，误报警表示数据的真实类别为正常却被判断为发生故障，漏报警表示发生故障未被检测出来被判断为正常。

从检测结果中可以看出，两个样本的检测正确率都在90%以上，误报警较低，漏报警较高。

表2 故障检测结果

4 结论

本文依据压缩机试验台数据，通过引入传感器故障，得到有效的故障训练数据和检测数据。

在压缩机试验台系统中，不同工况下的数据差异很大，同时检测会影响检测准确率。所以先通过减法聚类进行工况自适应分类，然后将数据按工况进行支持向量机故障检测。故障结果表明，减法聚类可以有效地进行自适应分类，支持向量机模型有较好的检测正确率。

本文只检测了传感器固定偏差这一种故障，后续研究将会在试验台中引入多种故障进行实验与故障诊断验证。

[1] 清华大学建筑节能研究中心. 中国建筑节能年度发展研究报告[R]. 北京: 中国建筑工业出版社, 2009: 1-79.

[2] HYVARINEN J, KARKI S. Building Optimization and Fault Diagnosis Source Book[M]. Finland: Technical Research Centre of Finland, VTT Building Technology, 1996: 25-26.

[3] PIETTE M A, KINNEY S, HAVES P. Analysis of an information monitoring and diagnostic system to improve building operations[J]. Energy and Buildings, 2001, 33(8): 783-791.

[4] WESTPHALEN D, ROTH K W. System and component diagnostics[J]. ASHRAE Journal, 2003, 45(4): 58-59.

[5] PATTON R J, CHEN J. Robust fault detection of jet engine sensor systems using eigenstructure assignment[J]. Journal of Guidance, Control and Dynamics, 1992, 15(6): 1491-1497.

[6] DORR R, KRATZ F, RAGOT J, et al. Detection, isolation, and identification of sensor faults in nuclear power plants[J]. IEEE Transactions on Control Systems Technology, 1997, 5(1): 42-60.

[7] AGOGINO A M, SRINIVAS S, SCHNEIDER K. Multiple sensor expert system for diagnostic reasoning, monitoring, and control of mechanical systems[J]. Mechanical Systems and Signal Processing, 1988, 2(2): 165-185.

[8] DUNIA R, QIN S J, EDGAR T F, et al. Identification of faulty sensors using principal component analysis[J]. AIChE Journal, 1996, 42(10): 2797-2812.

[9] DU Z M, JIN X Q. Multiple faults diagnosis for sensors in air handling unit using Fisher discriminant analysis[J]. Energy Conversion and Management, 2008, 49(12): 3654-3665.

[10] 陈玲, 杜志敏, 晋欣桥, 等. 压缩机性能试验台的测控可靠性研究[J]. 制冷技术, 2016, 36(3): 24-32.

[11] 张昉, 陈玲, 杜志敏. 基于不确定度评定及其线性规划的压缩机性能试验台传感器选配优化[J]. 制冷技术, 2016, 36(1): 7-13.

[12] GBT 5773-2004 容积式制冷剂压缩机性能试验方法[S].

[13] 董天禄. 离心式和螺杆机式制冷机组发展综述[J]. 制冷技术, 2001, 21(4): 6-9.

[14] 彭璐. 支持向量机分类算法研究与应用[D]. 长沙: 湖南大学, 2007.

[15] MAJI S, BERG A C, MALIK J. Classification using intersection kernel support vector machines is efficient[C]// Computer Vision and Pattern Recognition. Anchorage: IEEE Press, 2008: 1-8.

[16] SCHOLKOPF B, SUNG K, BURGES C, et al. Comparing support vector machines with Gaussian kernels to radial basis function classifiers[J]. Signal Procesing, 1997, 45(11): 2758-2765.

[17] WESTON J, WATKINS C. Multiclass support vector machines[R]. London: Department of Computer Science, University of London, 1998.

[18] 林升梁, 刘志. 基于RBF核函数的支持向量机参数选择[J]. 浙江工业大学学报, 2007, 35(2): 163-167.

[19] 王智锐, 唐汝宁. 基于支持向量机算法的空调负荷预测及实验研究[J]. 制冷技术, 2013, 33(4): 28-31.

[20] 王磊, 姜德凡, 李征涛, 等. 全自动制冷压缩机性能测试试验台的研制[J]. 制冷技术, 2006, 26(2): 5-7.

Research on Fault Diagnosis Method Based on Subtractive Clustering and Support Vector Machine

CHEN Ling, CHEN Zhijie, DU Zhimin*, JIN Xinqiao, FANG Xing

(Institute of Refrigeration and Cryogenics, Shanghai Jiao Tong University, Shanghai 200240, China)

The test system for volume refrigerant compressor performance is built according to GB/T 5773-2004. The accuracy and reliability of the test system entirely depend on the reliability of the sensor. In the paper, a method combined with subtractive clustering and support vector machine was designed to detect fault of the sensor of the test system. Subtraction clustering is used to classify working condition according to data from system. The support vector machine is used to detect fault according to classified working condition data. Experimental results show that, the method combined with subtractive clustering and support vector machine can detect sensor with fixed deviation fault effectively. Fault detection accuracy rate is more than 90%.

Compressor test system; Subtractive clustering; Support vector machine; Fault detection

10.3969/j.issn.2095-4468.2018.04.101

*杜志敏（1977-），男，副教授。研究方向：制冷空调故障诊断。联系地址：上海市东川路800 号上海交通大学制冷与低温工程研究所，邮编：200240。联系电话：021-34206533。E-mail：duzhimin@sjtu.edu.cn。

本论文选自2016年第九届全国制冷空调新技术研讨会。