基于GRA与回归分析法的青少年超重原因间的关系研究
2018-11-21王涵张雷
王涵,张雷
基于GRA与回归分析法的青少年超重原因间的关系研究
王涵,张雷
(重庆交通大学,重庆 400074)
近年来,青少年肥胖比例日益增高,这严重影响了该群体的身心健康,同时也引发了极为广泛的社会关注。为了研究该群体肥胖与运动水平与高卡路里食物摄入量之间的关系,主要采用灰色关联分析法(GRA)与回归分析法辅以说明。利用GRA分析了这两个因素与肥胖率之间的相关性,得到男童、女童的运动量与肥胖率的相关系数依次为0.574和0.576,美国、中国、西班牙、新西兰、南非5个国家的食物摄入量与肥胖率的相关系数依次为0.537,0.735,0.658,0.676,0.694.用回归分析法对运动量、食物摄入量和肥胖率进行分析,得到回归方程,通过对模型的改进得到决定系数为0.94的回归模型。最后可确定由这两个因素作为自变量与因变量肥胖率之间的函数关系。
青少年肥胖;运动水平;食物摄入量;灰色关联分析法
肥胖是一种严重的内科疾病,可引起多种并发症。不可避免地,整个社会将为此付出许多代价。其中,青少年肥胖问题更是社会关注的焦点。究其肥胖原因,就其中运动水平与高卡路里食物摄入量这两个因素而言,现有研究[1]并没有明确指出最主要的因素。因此,本文将采用灰色关联分析法与回归分析法对青少年肥胖与这两个因素之间的关系进行深入研究与比对。
1 问题分析
青少年肥胖是由于运动过少或太多而增加低成本和高热量摄入吗?本文认为肥胖与两个因素都有关。在研究方法上,本文分为两个步骤进行讨论:①分析两个因素即运动和食物摄入量与肥胖率之间的相关性,得到其相对应的相关系数;②通过查询到的相关数据对此进行回归分析,得到单个因素的函数关系式,进而结合两个因素得到一个共同的函数关系式。由于搜集数据比较困难,本文采用BMI数据来量化肥胖程度,即按照男女的运动量和相对应的BMI来划分。由于高卡路里食物摄入量与国家经济水平有密切关系,因此本文选用人均GDP数据来量化肥胖程度,即选取了5个国家1975—2015年的人均GDP数据。
2 灰色关联分析法
灰色关联分析是根据因素之间的发展趋势的相似或相异的程度,即灰色关联度,作为评价因素间的关联程度的一种方法。而该方法广泛应用于分析事件原因、方案改进与优化、竞争力综合评价等评估研究中[2]。本文将利用该方法并结合回归分析法确定青少年肥胖与运动水平和高卡路里食物摄取量这两个影响因素之间的关系。
3 灰色关联分析模型的建立
3.1 相关性分析
为消除数据量纲的不同,需要对数据进行预处理,即将所有的数据除以第一个数据,可得到一个新序列。记两组数据为:
i=[i(1),i(2),i(3),…,i(),…,i()],=1,2,…,;
j=[j(1),j(2),j(3),…,j(),…,j()],=1,2,…,.
则计算公式为:


3.2 模型的求解
将从世界银行所获取的运动量数据和选取的5个国家的1975—2015年的GDP数据分别与BMI数据相对应代入上述模型,结果如表1所示。同时可得到美国、中国、西班牙、新西兰、南非5个国家的食物摄入量与肥胖率的相关系数依次为0.537,0.735,0.658,0.676,0.694.
表1 运动量与肥胖相关系数
性别缺乏运动组低运动组基本运动组活跃组高度活跃组平均关联系数 男10.6530.491 40.392 30.333 30.574 0 女10.665 50.488 10.3940.333 30.576 2
3.3 结果分析
从表1中可发现男生的运动量与肥胖相关系数为0.574 0,女生为0.576 2,都是中等程度相关且两者差异不大。因此,男女可不用分开讨论。从图1可发现美国的相关系数为0.537最低,中国的相关系数为0.735最高,美国为中等程度相关,中国、西班牙、新西兰和南非都为强相关。综上所述,肥胖与运动和食物摄入量都是密切相关的,验证了本文最开始的想法。
4 回归分析模型的建立
4.1 基本模型
为了大致地分析与1和2的关系,利用数据分别作出与1和2的散点图。运动量与肥胖率的关系如图1所示,高卡路里食物摄入量与肥胖率的关系如图2所示。
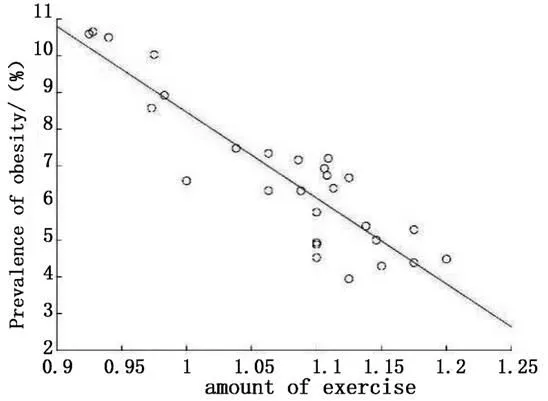
图1 运动量与肥胖率的关系

图2 高卡路里食物摄入量与肥胖率的关系
从图1、图2可发现,随着1的增加,的值有比较明显的线性减少的趋势,图中直线是线性模型=0+11+拟合的(其中是随机误差)。而在与2的散点图中,当2增大时,先弯曲向上增长,再弯曲下降,图中的曲线是三次函数模型=0+12+222+323+拟合的。
综上所述,结合线性模型和三次函数模型建立回归模型=0+11+22+322+423+,模型右端的1和2称为回归变量,0+11+22+322+423是给定运动水平1,人均收入2是肥胖率的平均值,0,1,2,β,4为回归系数。
4.2 模型的求解

4.3 结果分析
得到回归系数估计值及其置信区间(置信水平=0.05),检验统计量2,,,2的结果如表2所示。其中,2=0.859 7指因变量(肥胖率)的85.97%可由模型确定,远小于,因而模型从整体上来看是可用的。最后的函数表达式为:=21.089-14.257 81-3.724 42+20.047 422-14.538 523.
表2 基本模型计算结果
参数参数估计值参数置信区间 β021.089[9.873 0,32.305 0] β1﹣14.257 8[﹣23.990 0,﹣4.525 5] β2﹣3.724 4[﹣16.677 1,9.228 4] β320.047 4[﹣11.207 0,51.301 7] β4﹣14.538 5[﹣34.719 0,5.641 9] R2=0.859 7,F=35.245 5,p<0.000 1,s2=0.666 6
4.4 模型的改进
上述模型中回归变量1和2对因变量的影响是相互独立的,即肥胖率的均值与人均收入2的三次关系由回归系数2,3,4确定,而不依赖于运动水平1.同样肥胖率的均值与运动水平1的线性关系由回归系数1确定,不依赖于2.猜想人均收入与运动量之间的交互作用会对产生影响,用1和2的乘积代表他们的交互作用,于是模型增加一项,得到=0+11+22+322+423+512+6122+.
这个模型中,的均值与2的三次关系为(2+51)2+(3+61)22+423,由系数2,3,β,5,β确定,并依赖于运动水平。同理可求的改进模型后的参数估计值与参数置信区间(2=0.936 6,=51.722 1,p<0.000 1,2=0.329 9),进而得到新的函数关系为:=17.152 3+18.949 81+172.244 42-144.021 322+4.946 423-148.778 212+121.371 7122.改进前后运动量和食物摄入量与肥胖的关系如图3、图4所示。
4.5 结果分析
相比可知2有所提高,说明改进后的模型有效,而且交互作用项的系数5和6不包含0点,所以有理由相信改进后的模型更符合实际。
5 结束语
通过改进后模型所得图4可以观察到,高肥胖率集中在高卡路里食物摄入量高数值与运动量低数值区,而在其他数值组合区域将呈现出符合最终函数关系的变化状态。因此在对青少年肥胖的原因研究上,对于运动水平和高卡路里食物摄入量这两个因素的函数关系,最终确定为:=17.152 3+18.949 81+172.244 42-144.021 322+4.946 432-148.778 212+121.371 7122.这将为青少年肥胖改善的相关探讨提供一定的实验依据,从而对解决这一社会问题贡献出一份力量。

图3 改进前运动量和食物摄入量与肥胖的关系
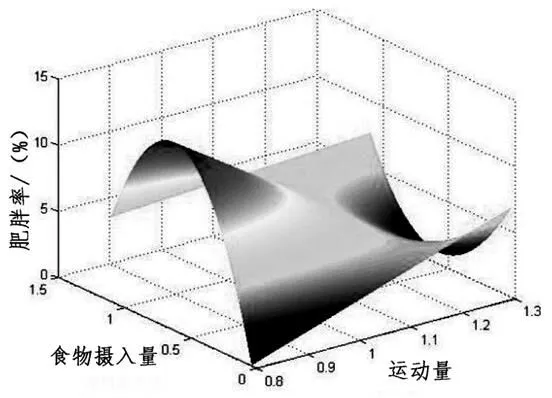
图4 改进后运动量和食物摄入量与肥胖的关系
[1]Janssen I, Katzmarzyk P T, Boyce W F,et al.Comparison of overweight and obesity prevalence in school-aged youth from 34 countries and their relationships with physical activity and dietary patterns[J].Obesity reviews,2005,6(2):123-132.
[2]黄速建,李倩,王季.我国不同所有制工业企业效率比较评价——基于熵权法和灰色关联分析法的分析[J].河北经贸大学学报,2017,38(3):72-79.
[3]刘红亮,李成付.数学建模与模型算法[M].北京:科学出版社,2016.
2095-6835(2018)21-0073-02
R589.2
A
10.15913/j.cnki.kjycx.2018.21.073
王涵(1996—),女,重庆人,本科,研究方向为人文地理与城乡规划。
张雷(1980—),男,重庆人,副教授,研究方向为复杂网络、优化控制。
〔编辑:严丽琴〕
