基于正态云-模糊可变耦合模型的水环境质量评价

高玉琴， 赖丽娟， 姚 敏, 张泽宇

(1.河海大学 水利水电学院， 江苏 南京210098； 2.江苏省水文水资源勘测局， 江苏 南京210029)

1 研究背景

随着社会经济高速发展，大量污染物排放到水体中对水环境构成威胁，也制约社会经济的可持续发展。水环境质量评价是指为了解水环境情况建立模型，对水体进行水质等级、污染情况评价，分析水环境质量分布规律和污染原因，提出有针对性的改善措施[1-2]。国内外现有的水环境质量评价方法有：单因子评价法、模糊层次分析法、灰色评价法、人工神经网络法、集对分析、主成分分析法和云模型等[3]。杨增宝等[4]应用理想点法研究北京市朝阳区地下水水质情况，构建了理想点评价函数，确定各等级下的理想点贴近度，从而给出评价结果；杜明亮等[5]基于熵权与超标倍数赋权法改进权重，应用集对分析法研究淮东水源地水质情况；徐光宇等[6]运用主成分分析法对汾河太原城区段水质评价，考虑各个指标的关联性，利用降维思想，将多指标简化为若干个彼此不相关的综合指标，通过对这些综合指标的评价分析。

本文提出正态云-模糊可变耦合评价模型。该模型的特点有：(1)利用相对最小熵根据层次分析法权重w1i和熵权法权重w2i获得组合权重wi，该方法避免了权重确定过程中过于主观或客观的弊端；(2)运用正态云模型对模糊可变的相对隶属公式的线性进行改进，兼顾了评价的模糊性和随机性；(3)采用模糊识别模型判断水质级别，避免了最大隶属度小于剩余隶属度总和时结果不合理的问题，同时级别特征值H用于同级别间的比较。最后将该评价模型运用到2016年秦淮河水环境质量评价中，评价结果与单因子指数评价法、模糊综合评价法和云模型进行比较，验证正态云-模糊可变评价模型的可行性和有效性。

2 正态云-模糊可变评价模型

2.1 云模型

云模型(Cloud model)是李德毅等[7]提出的基于模糊性和随机性的一种定性与定量相互转换模型，正态云模型在作为正态隶属度函数时具有普适性。当前正态云模型发展较为成熟，已应用到时间序列预测、质量评价、风险评估和空间数据挖掘等领域。

云模型将定性概念A映射到论域U上，论域U中任意元素x对概念A都有一个稳定倾向的随机数UA(x)，即确定度。在水环境质量评价中U为水环境等级对应的区间，x是某次的水质实测值，A代表水环境质量评价的级别。

云模型由特征值反映水环境质量评价的不确定性、模糊性，由云发生器进行定性和定量的转换。特征值包含期望(Ex)、熵(En)和超熵(He)。其中，期望(Ex)指水环境质量评价论域U中最具代表的典型样本点，即所有云滴的平均值；熵(En)是水环境质量评价中模糊性和离散性的度量，代表论域中可被接受的范围；超熵(He)是水环境质量评价中模糊性和随机性的关联，反映熵的不确定性度量[8]，3个特征值的计算见公式(1)。

(1)

云发生器分为3种：(1)将定性转化为定量的正向云发生器(FCG)，即通过云C(Ex、En、He)产生定量云滴xi与隶属度μi；(2)由定量转换为定性的逆向云发生器(BCG)，即通过精确的Drop(xi)转换到定性概念C(Ex、En、He)进行分析；(3)由X云发生器与Y云发生器构成特殊的条件云发生器，即已知C(Ex、En、He)和特定条件X或者Y来计算确定度。水环境质量评价通过X条件云发生器来实现定性与定量的转换，如图1所示。

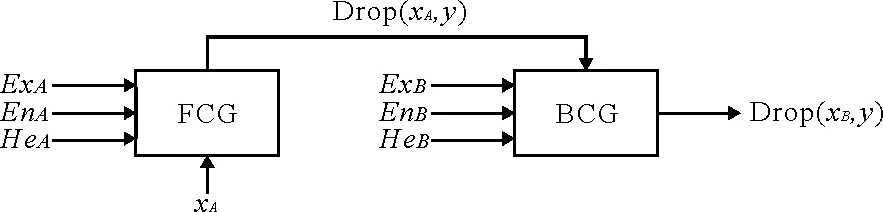
图1 单条件单规则云发生器

2.2 模糊可变集合

可变模糊集理论是陈守煜[9]以模糊理论和辩证唯物论为基础，提出了隶属度与隶属函数动态可变概念。其中，相对差异函数、相对隶属函数理论修正Zadeh的模糊集合隶属函数的唯一、静态化缺点。模糊可变集已应用到模糊水文学、农田水利和电力系统的调度等领域。

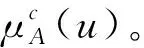
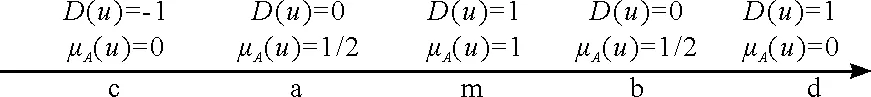
图2相对差异函数图

其中[a,b]为吸引域，[c,a]、[b,d]为排斥域，m=(a+b)/2。

模糊可变识别模型是在已知隶属度和权重的情况下，通过识别对象级别特征值H分析评价对象级别[10]，模型公式见公式(2)和(3)。

(2)

(3)

式中:h为等级数(h=1，2，…，c)；i为指标数(i=

1，2，…，m)；uh为识别对象指标综合相对隶属度；wi为指标权重；m为识别指标数；α为模型优化准则参数，α=1为最小一乘方准则，α=2为最小二乘方准则；p为距离参数，p=1为海明距离，p=2为欧式距离。通过变换模型参数α，p，可模拟指标值与标准值间的不同关系[11]。

2.3 模型参数

2.3.1 云模型 双边约束时，云模型结合模糊可变理论中相对差异度理论，将在接近指标边界值对相邻等级的确定度趋近于0修正为1/2，有利于评价结果的区分。因此对参数公式(1)修正后得公式(4)。

(4)

式中:Sih,max，Sih,min分别是第i个指标在h等级中的上下限。

2.3.2 隶属函数 运用正态云模型对模糊可变集的相对隶属函数的线性，使水环境质量评价指标对各等级的隶属度符合正态分布规律，具有更好的模糊性、随机性。根据确定的云模型参数(Ex，En，He)和X条件云发生器生成评价指标对各评价等级的吸引隶属度μA(u)(见图3)。

图3 吸引隶属函数对比图

设第i个指标的实测值为ui，由云模型计算第i个指标对h级别的吸引隶属度为μA(uih)。根据《地表水环境质量标准》(GB3838-2002)，将水环境分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、劣Ⅴ(h=1，2，…，6)共6个级别。第i个指标的相对隶属矩阵公式如式(5)、(6)所示。

对于越大越优型指标：

xi≥Exih时，μA(ui,h-1)=1-μA(uih);

μA(uik)=0 (k≠h,k≠h-1)

xi≤Exih时，μA(ui,h+1)=1-μA(uih);

μA(uik)=0 (k≠h,k≠h+1)

(5)

对于越小越优型指标：

xi≤Exih时，μA(ui,h-1)=1-μA(uih);

μA(uik)=0 (k≠h,k≠h-1)

xi≥Exih时，μA(ui,h+1)=1-μA(uih);

μA(uik)=0 (k≠h,k≠h+1)

(6)

根据公式(2)计算综合相对隶属度uh，变换参数p,α，以4个模型的平均值代入公式(3)可得级别特征值H，用于水环境质量评价。

2.3.3 组合权重 本文运用层次分析法和熵权法确定权重，基于最小相对熵原理进行权重组合，既要考虑指标的重要性，也要考虑评价指标实际数的差异性。层次分析法对评价指标进行两两间比较构造判断矩阵dij，根据幂法计算评价指标的权重值w1i，并对权重进行归一化和一致性检验[12]。熵权法权重w2i随数据取值变化而变化，能够充分利用原始数据信息，权重值更加合理、客观[13]。

组合权重wi采用最小相对熵原理[14]对w1i和w2i进行组合，避免权重过于主观和缺乏重要性比较，组合公式如下所示。

(7)

式中：w1i为层次分析法第i个指标权重；w2i为熵权法第i个指标权重；wi为第i个指标的综合权重。

2.4 评价流程

正态云-模糊可变耦合模型的评价流程如图4所示：

(1)选取合适的水环境质量评价指标，根据公式(4)和水环境等级限值确定云模型参数；

(2)采用组合公式(7)，确定评价指标组合权重wi；

(3)通过正向云发生器计算吸引隶属度μA(uih)，根据公式(5)、(6)确定隶属矩阵；

(4)运用公式(2)、(3)对隶属函数和指标权重进行计算，确定级别特征值H，实现水环境的质量评价。

3 秦淮河水环境质量评价实例研究

3.1 秦淮河概况

秦淮河本名为龙藏浦，是长江下游右岸的一条支流，源于溧水县的溧水河和句容县的句容河，按照地理条件可分为:秦淮河上游、秦淮新河、外秦淮河和内秦淮河，如图5所示。

根据省政府对《江苏省地表水环境功能区划分批复》(苏政复〔2003〕29号)，对秦淮河段水环境功能区进行划分，不同水环境功能区监测断面水质要求如表1所示。

3.2 评价指标选择

秦淮河主要受生活污水和工业废水的污染，其中有机物污染和富营养化情况严重[15]。根据2016年秦淮河汛期和非汛期实测数据的平均值，和我国现行的《地表水环境质量标准》(GB3838-2002)分析秦淮河水环境情况。水环境质量评价指标及标准如表2所示。

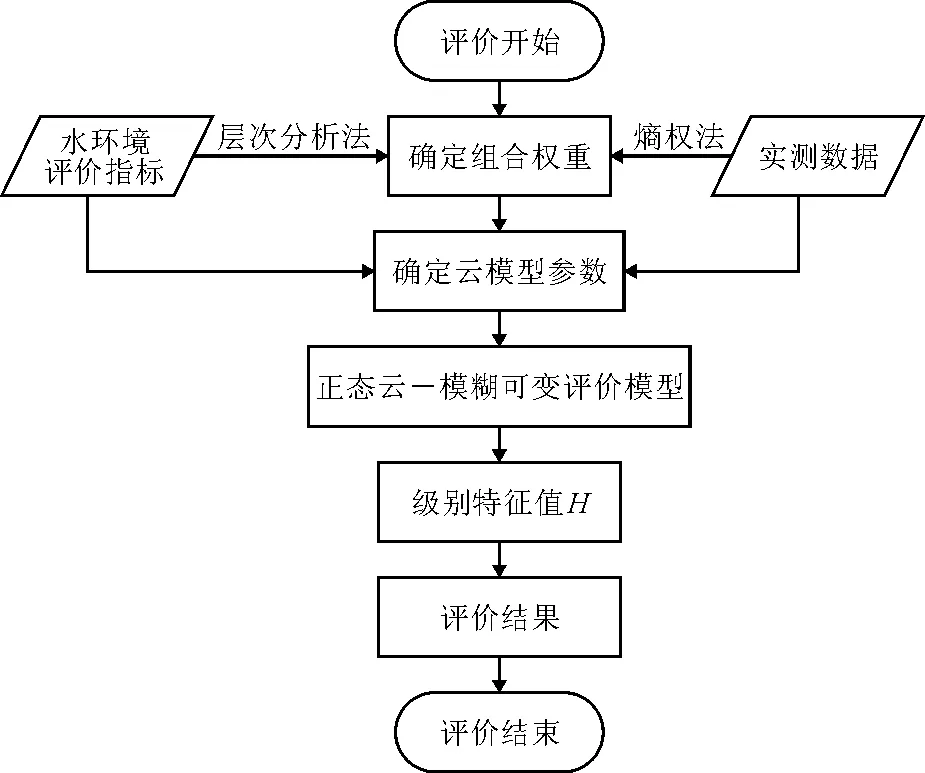
图4 正态云-模糊可变评价模型评价流程图

图5 秦淮河流域图

3.3 评价结果

采用层次分析法和熵权法分别可得权重w1i和w2i，运用组合公式(7)可得水环境质量评价指标组合权重wi，如表3所示。

根据云模型的参数公式(4)和《地表水环境质量标准》(GB3838-2002)确定云模型参数，如表4所示。

3.3.1 可行性分析 本模型评价结果与单因子指数评价法、模糊综合评价法和云模型方法进行比较，2016年秦淮河水环境质量的评价结果比照如表5所示。

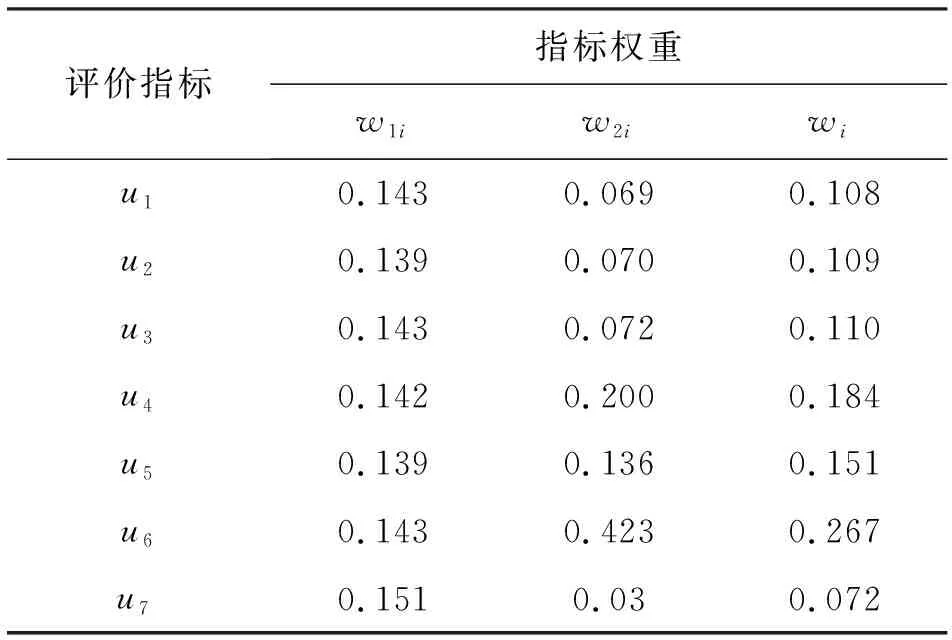
表3 秦淮河评价指标权重

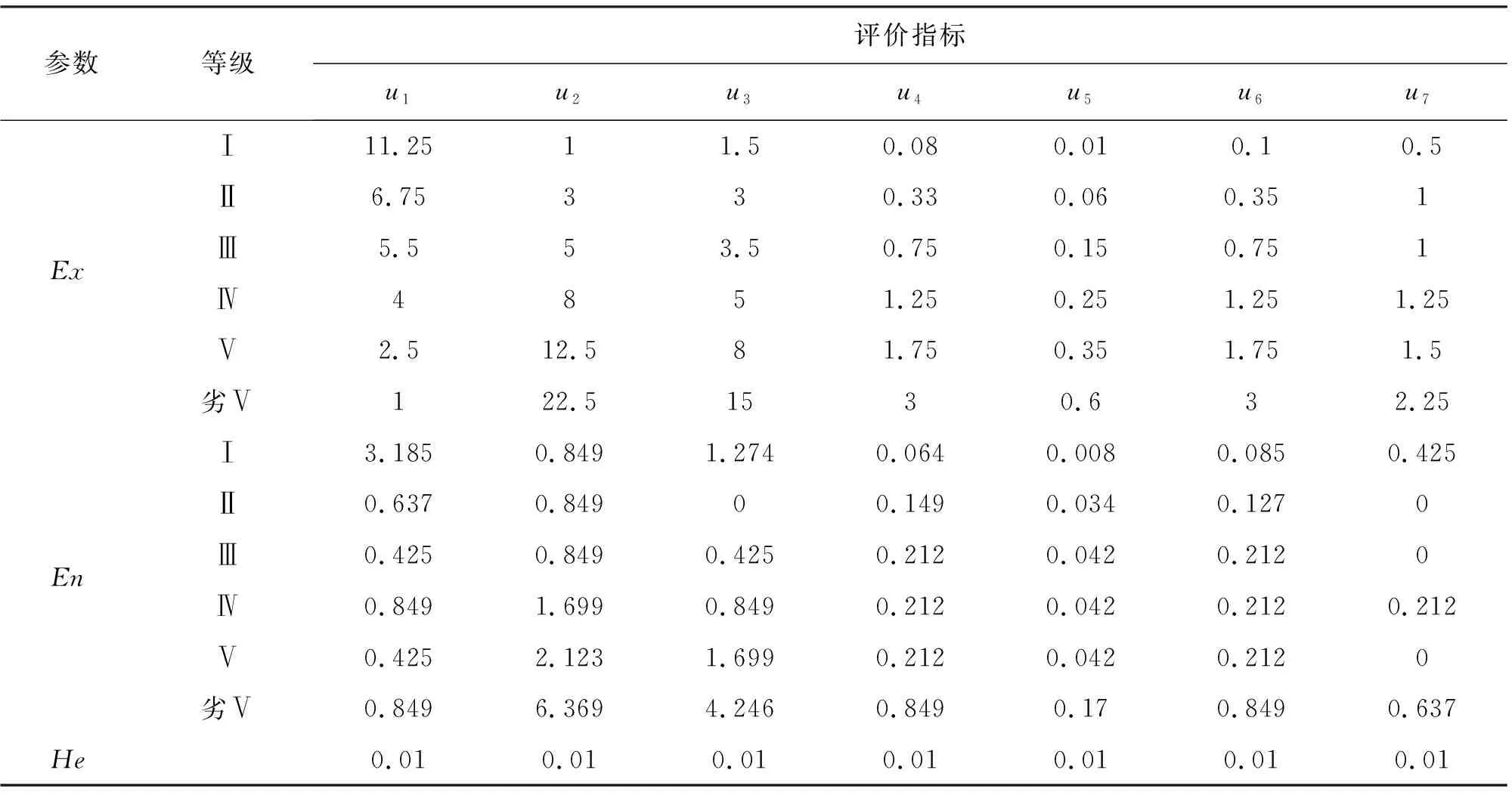
表4 云模型参数

如上表可见，对4种评价结果进行比较分析可得：(1)当其他3种评价方法的评价结果都为劣Ⅴ时，本模型评价结果优于劣Ⅴ。对比研究可知，在劣Ⅴ的相对隶属度确定时，单因子指数法和模糊综合评价法是xi≥Si5时μA(ui6)=1，其评价结果大都为劣Ⅴ类。根据图3，当xi≥Si6时μA(ui6)=1，该模型对Ⅴ评定区间 [Si5,Si6]划分更加准确，评价结果更为合理。

(2)当其他3种评价的结果不全为劣Ⅴ时，本模型的评价结果介于其他评价结果之间，表明模糊识别解决了最大隶属度小于剩余隶属度总和的情况，其评价结果介于最大和最小隶属度评价结果之间，更加合理。

3.3.2 秦淮河水环境分析 由级别特征值公式(2)、(3)计算分析秦淮河水环境等级。当H∈[1,1.5]时为Ⅰ级；当H∈(1.5,2.5]时为Ⅱ级；当H∈(2.5,3.5]时为Ⅲ级；当H∈(3.5,4.5]时为Ⅳ级；当H∈(4.5,5.5]时为Ⅴ级；当H∈(5.5，∞]时为劣Ⅴ级，秦淮河汛期、非汛期级别特征值H结果如表6所示。

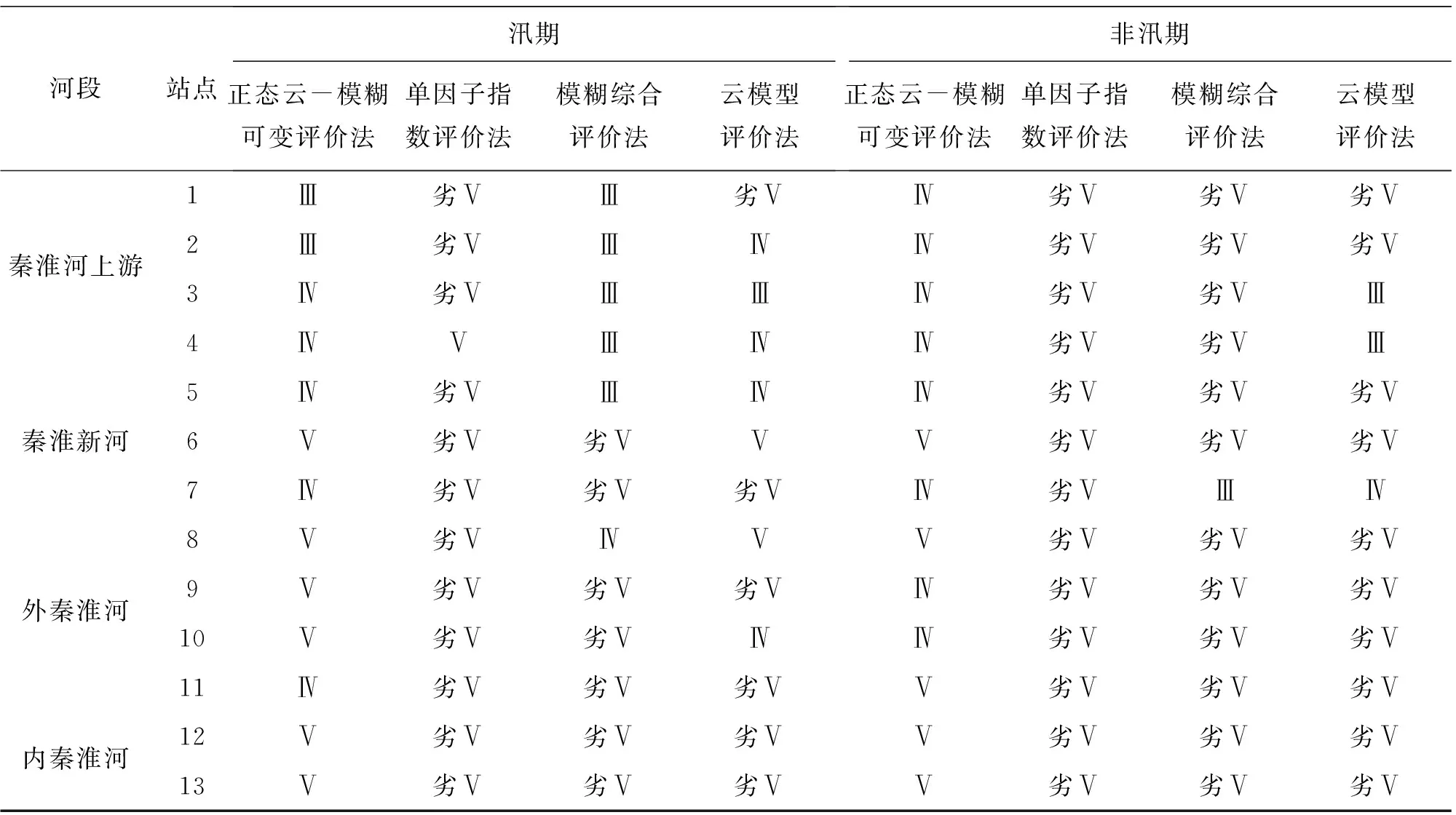
表5 2016年秦淮河水环境质量评价结果比照表

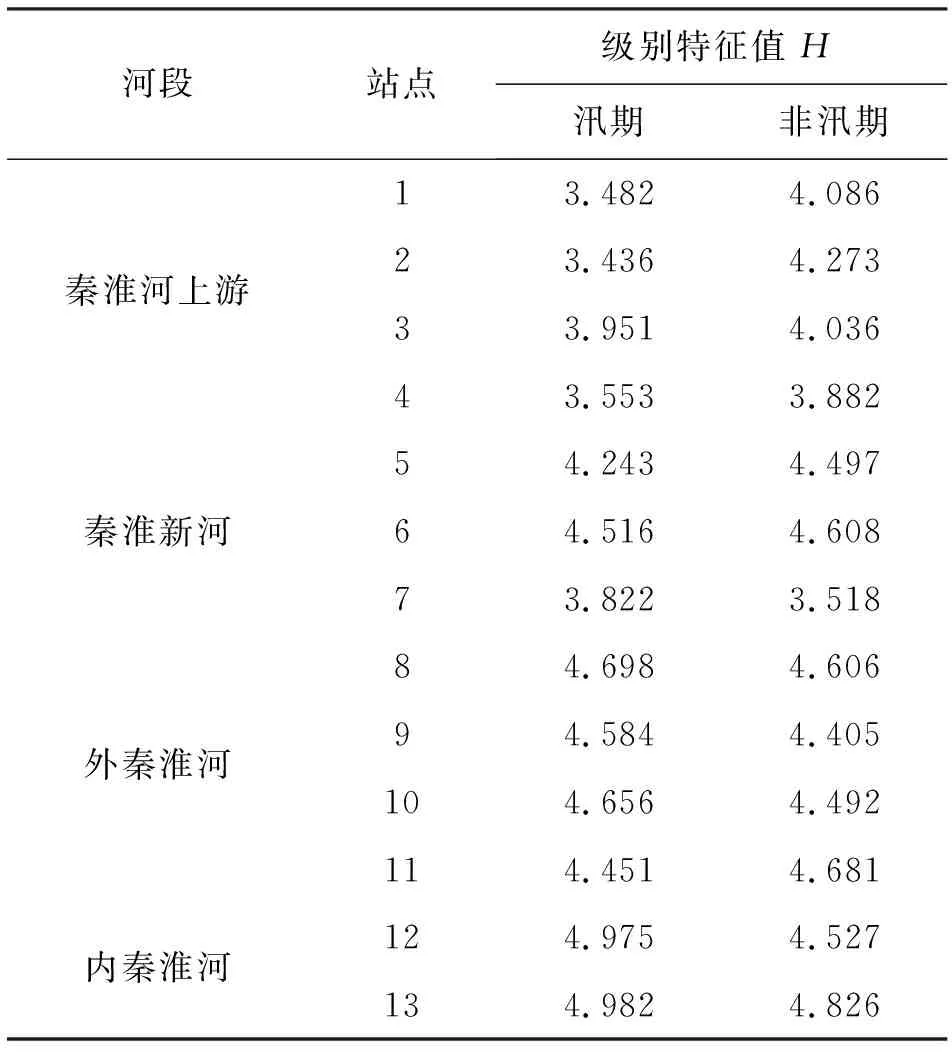
表6 秦淮河汛期、非汛期级别特征值H

由表6可见，级别特征值H越小则水环境越好。(1)在秦淮河上游和秦淮新河段，汛期水量增加提高了水环境承载能力，故汛期水环境优于非汛期水环境。其中，秦淮新河闸监测点7在非汛期进行“引江换水”工程[16]，非汛期水环境优于汛期水环境。秦淮河上游和秦淮新河主要受城镇居民生活用水、江宁污水处理厂和部分工业废水影响，水环境在Ⅲ、Ⅳ类间波动，表现出典型的城镇生活与工业污水污染等特征。(2)在内、外秦淮河段，汛期期间加快了河岸的污染物排入河流中，故汛期水环境劣于非汛期水环境。沿河为城市居民生活区，水环境稳定于Ⅴ类，表现出典型的城市生活及餐饮等“三产”污水污染特征。

4 结论和讨论

针对水环境质量评价存在的模糊性、随机性和最大隶属度不严谨等问题，引入相对最小熵原理、云模型和模糊可变集概念，提出正态云-模糊可变耦合模型。

(1)正态云-模糊可变耦合模型有效刻画了评价中评价标准和指标隶属的模糊性、随机性。其中，级别特征值H有效解决了在水环境等级的判断和同级别间的比较问题，组合权重综合考虑了主、客观因素，符合实际。运用该模型评价秦淮河流域2016年的水环境，评价结果同单因子指数评价法、模糊综合评价法和云模型评价法进行对比，验证正态云-模糊可变耦合模型评价结果更合理有效可靠。

(2)基于正态云-模糊可变耦合模型的水环境质量评价研究结果表明，秦淮河表现出城镇工业、生活等污染特征，需要引起环境等相关部门的重视，并积极采取应对措施。

对于如何确定云模型参数，没有统一的意见，笔者结合模糊可变理论，将边界对相邻级别的隶属度为1/2来确定En参数。虽在结合模糊识别模型时，云模型表现出良好的可行性，但在单独运用该模型时，其可行性仍然未知，同时刻画的隶属度是否合理且有实际意义，都需要进一步研究。