舰船载船浮箱下水的结构分析与优化
2018-11-20周清华蔡乾亚
周清华,魏 波,陈 震,蔡乾亚
(1. 江南造船(集团)有限责任公司,上海 201913;2. 上海交通大学,上海 200240)
0 引 言
船舶下水是在船舶建造工程大部分完工之后,将船舶从船台上移至水域的工艺过程,是船舶建造的一项重要组成部分。目前船舶下水的主要方式有:纵向重力式下水、船坞下水、气囊式下水和载船浮箱下水等。其中载船浮箱下水是一种新的下水工艺,具备更好的保密性和经济性。
载船浮箱下水的载船系统是由短纵梁、横梁、墩木和具有升降、自动卸载及行走功能的液压小车等部件组成,典型支撑图如图1所示。载船系统的受力分析是浮箱载船下水工艺研究中的一项关键技术。但由于载船系统部件之间的非线性接触关系以及小车具有自动卸载功能,这些特点使受力分析变得非常复杂[1]。
对于首次采用载船浮箱下水方式的万吨级大型舰船而言,要综合考虑船型设计特点、深水坞水位限制、支撑系统布置条件等多种因素的影响,下水技术难度极大。为此,有必要开展下水工艺和关键技术攻关,通过载船浮箱下水多种方案的对比分析、论证和优化,选择最优的下水工艺,提高下水过程中的安全性与可靠性。

图1 典型支撑图Fig.1 Typical support
1 载船浮箱下水计算方法
1.1 舰船规范
舰船规范规定了舰艇坐坞时的船体总纵强度、局部强度和坞墩强度计算方法[2]。对于坞墩面积有限的大型舰船,难以满足坞墩载荷校核和尾部中内龙骨强度校核要求,舰船规范偏于保守。同时该方法仅考虑了龙骨墩承载状态,无法考虑楔形边墩情况。可见,采用舰船规范计算方法具有较大的局限性。
1.2 一维梁简化计算
在船台顶升和浅水坞起浮、坐底阶段,采用了一维梁简化计算方法求解载船系统的支墩反力。基于薄壁梁理论并结合实际下水工艺,根据载船系统受力特点,把下水模型简化为变刚度弹性基础上的变断面耦合梁力学模型[3]。其中,使用接触单元模拟楞木和船体的接触关系,考虑弹性梁之间的变形耦合作用和接触、卸载两重静力非线性迭代问题。采用弹簧单元模拟浮力,在浮箱的总纵强度计算中考虑了流体静压力分布和浮箱变形之间的相互影响,使计算结果更趋近于实际情况[4]。图2为船体和浮箱双梁耦合计算模型。

图2 船体和浮箱双梁耦合计算模型Fig.2 Hull-pontoon beam coupling calculation model
该方法的建模工作量小,足以满足一般的工程应用要求,但对各支撑点等效组合刚度的计算精度要求高,同时无法模拟船宽方向不同支撑点的刚度差异对支反力的影响。
1.3 整船三维有限元分析
采用整船三维有限元分析方法不仅可以准确地模拟船体、支撑系统和浮箱之间的变形耦合效应和主要构件刚度特征,计算部分边墩拆除后和首部楔形边墩的局部载荷分布,有效地避免了在支撑系统串、并联耦合状态下的等效组合刚度计算误差的影响。图3为整船三维有限元分析的流程图。
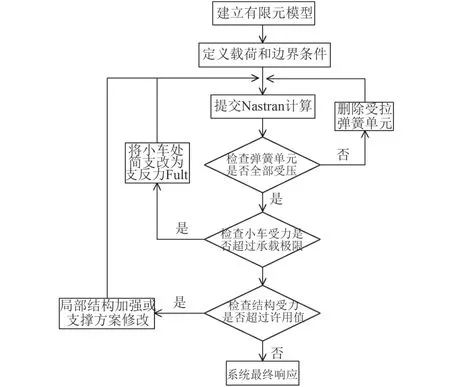
图3 分析流程Fig.3 Analysis flow chart
2 工程应用与分析
2.1 深水坞
载船浮箱下水过程主要可分为以下4个步骤:
1)用液压小车把坐落在船台上的船舶抬起,平移至上坞阶浮箱上,然后落墩、撤掉全部小车;
2)向坞内注水使载船浮箱起浮,调整浮箱浮态,然后横移到下坞阶上;
3)排出坞水,使载船浮箱搁于下坞阶上;
4)打开浮箱通海阀,向坞内注水至水位与海水平面持平,船舶起浮并脱离浮箱,完成整个下水过程。
与船台上和浅水坞内相比,深水坞内的船体承载状态和局部载荷发生了较大变化,具体如下:
1)综合考虑深水坞的最大水位限制、船体起浮后的正浮吃水、船体线型和支墩布置等因素,为了保证船体底部与坞墩之间的最小安全距离不小于0.3 m[5],经过浮态计算可知,深水坞内船体起浮之前,需拆除67%的边墩。
2)船体尾部为悬臂梁式,其长度与船长的比值为1/7,重量线性载荷为36 t/m。为了提供足够的垂向支撑作用,在船台上和浅水坞内均设有高、低连墩结构,但连墩结构与螺旋桨桨叶的横向间距仅为0.5 m,对船纵向出坞提出了严格的船体姿态要求。为了避免碰撞风险,需拆除高连墩,船先横移,后纵移出坞。
支撑点的减少和局部载荷的增大增加了船体结构的安全隐患,应准确计算支撑载荷,评估结构强度。
2.2 力学模型
整船三维模型包括船体、支撑系统和浮箱的所有纵向构件,横舱壁、肋骨框架等横向构件。桁材、肘板上的开孔和轻次舱壁忽略不计。网格大小一般采用纵骨间距×肋骨间距,支撑区域采用细网格,即1/4纵骨间距划分单元。采用弹簧单元模拟墩木,根据下水状态时的重量分布数据,等效为沿船长分布的垂向线载荷,并施加于船体舷侧外板上。
整船三维模型见图4。

图4 整船三维模型Fig.4 Global 3-D FEM
2.3 船体结构分析
2.3.1 船体变形
图5为船体梁在深水坞内、边墩拆除后、坐墩状态下的变形。

图5 船体梁变形Fig.5 Hull deformation
船体梁呈现为4节点垂向弯曲变形;较大变形集中出现在首、尾两自由端,最大变形值分别为7.9 mm和 31.0 mm。
2.3.2 支墩反力
支墩反力的大小和分布与船体重量和支撑点刚度的分布有关。通过多方案对比分析,确定了尾部支撑方案:尾部2连墩保留,增设垂向桁材、楞木和船台中墩等加强措施。图6为支墩反力计算结果。

图6 整船支墩反力分布Fig.6 Reaction force distribution of whole ship docking block
图6 可知,在深水坞内,边墩拆除后,支墩反力较大值均出现在尾部2连墩、首部600 t横梁和中部个别350 t横梁处。其中,尾部2连墩处的支反力最大,最大值为295 t。该接触区域的船体横隔板以剪切强度为主,计算得到在剪切强度安全系数0.4的要求下,尾部2连墩处的船体最大承载能力为436 t,结构强度安全裕度为32%。
2.3.3 船体底部
根据支墩反力和结构设计特点选择典型底部横舱壁、肋板的局部强度评估区域,并对开孔区域进行网格细化。由于船底肋板、横舱壁的弯曲变形与纵向结构弯曲变形正交,纵向弯曲应力对船底肋板、横舱壁的弯曲应力影响极小,故在模型中不施加垂向弯矩和剪力,仅将支墩反力等效为线载荷施加于相应的结构单元边界上即可。图7为底部肋板应力云图。
计算表明,船体底部应力峰值均小于许用应力,满足结构强度要求。
2.3.4 首部结构
船首结构为悬臂梁式、线型复杂、支墩反力大,为了避免小车顶升后的支反力超出许用值,采用了楔形支墩支撑方案,需重点校核其局部强度。假定楞木为小变形,并忽略楞木与船体、楔形边墩之间的静摩擦作用,即不考虑接触面内载荷。图8为首部600 t横梁楔形边墩上的接触压力计算值。
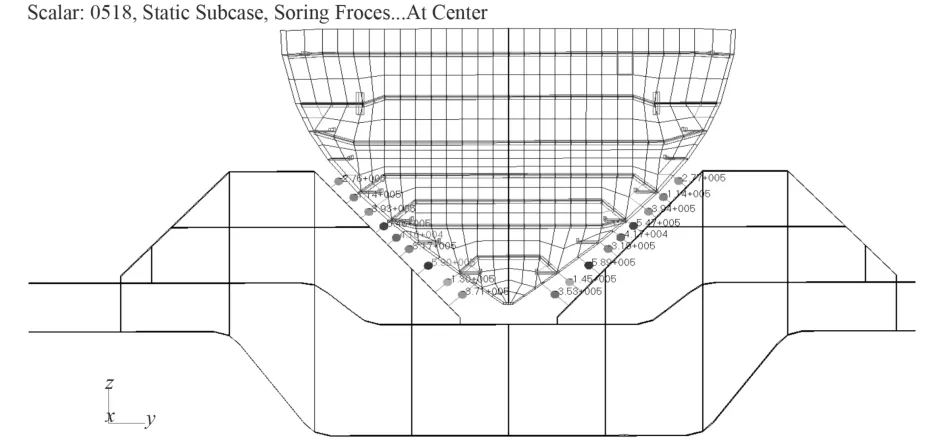
图8 首部接触压力分布Fig.8 Contact force distribution of forebody
由图8可知,由于接触区域的结构刚度大小、分布不同,船体与楔形边墩之间的接触压力并非线性分布,呈现为双峰曲线分布规律;峰值出现在楔形边墩的水平和垂向支撑板交接处,符合结构力学特性。
原始设计方案的结构最大应力为336 MPa,已超出许用应力308 MPa,不满足强度要求。通过对支撑区域采取增设肋骨和球扁钢的加强措施,有效地将高应力区域由船体横舱壁转移至加强肋骨的腹板上,较大幅度地降低了应力水平,最大应力仅为181 MPa,应力云图见图9。
2.4 支撑系统分析
采用局部模型计算典型支撑系统的最大承载能力。图10为施加载荷100 t后的船台中墩剪切应力云图。
基于船台阶段小车顶升后的支反力计算,将导流罩下的 350 t横梁换为 600 t横梁。将 600 t以点载荷的形式施加于横梁中部,定义小车与横梁接触处为简支约束。图11为600 t横梁应力云图。

图9 船首底部应力云图Fig.9 Forebody bottom Von.Mises stress

图10 船台中墩剪切应力云图Fig.10 Slipway mid-docking block shear stress

图11 600 t横梁应力云图Fig.11 600 t beam Von.Mises stress
由图11可知,600 t横梁的高应力区域为横梁距中2.5 m范围内、上下面板及转角的结构突变处,最大应力对称出现在横梁距中1.8 m的折角区域;600 t横梁的横梁的最大应力为197 MPa,小于许用应力280 MPa,故600 t横梁满足强度要求。但值得注意的是,当在浅水坞内,小车撤掉、船体落墩后,横梁两侧的支撑点间距由5 m增加至7.6 m,跨距增加致使横梁中部的弯矩增加52%,计算得到的最大应力为382 MPa。为了减小跨距,600 t横梁中部与浮箱之间的空隙内需增设墩木。
支撑系统的承载能力评估结果见表1。
由表1可知,支撑系统满足结构强度要求,并留有一定的安全裕度。

表1 支撑系统承载能力Tab.1 Capacity of support system
2.5 浮箱分析
浮箱的主要承载构件为中纵桁,其跨距仅为2 m,腹板高度为0.6 m,属于短深梁,以剪切强度为主。计算表明,在首部楔形边墩和尾部2连墩处的支反力作用下,中纵桁腹板的应力水平较高,部分单元的最大应力已达到许用应力的1.1倍。图12为浮箱加强方案,通过采取在纵桁腹板下端增设T型材的方法,增加了剪切面积,从而达到剪切强度要求。
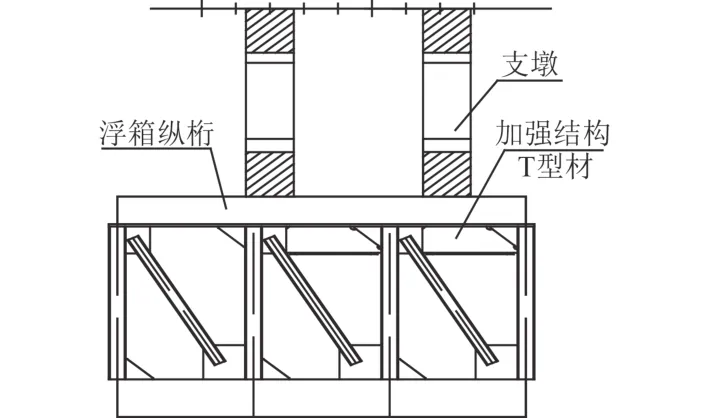
图12 浮箱加强Fig.12 Pontoon strengthen
3 结 语
整船三维有限元分析方法不仅可以有效地模拟船体、浮箱和支撑系统之间的组合刚度和变形耦合效应,准确获取支墩反力,而且计及了楔形边墩的影响,突破了传统计算方法的局限性。实践证明,采用整船三维有限元分析方法评估大型舰船载船浮箱下水的结构安全性切实可行,提高了下水过程的可靠性。
